应用于显屏驱动芯片的可精确调控图像色彩增强方法*

杨洪柏，张江安

(1.上海开放大学理工学院,上海 200433；2.上海工程技术大学高等职业技术学院,上海 200437)

近年来,随着电子技术、信息技术的高速发展,带有液晶(LCD)、有机发光二极管(OLED)显示器的便携式消费电子产品(如手机、平板电脑)得到普及,这些电子产品中显屏驱动芯片的设计越来越受到重视。早期,显屏驱动芯片的功能主要是接收主控芯片发送的数据流及控制信号流,为显示屏幕提供驱动电压/电流和阵列控制信号,实现图像显示功能[1-2]。随着产品的快速升级和演化,不少显屏驱动芯片增加了图像色彩增强(Color Enhancement,CE)功能,其目的是通过对图像数据进行处理,使得显示器呈现的图像色域更广,视觉效果更加艳丽。该功能既可提升某些饱和度偏低图像的显示效果,也可弥补某些类型显示器(如LCD 显示器)色域不宽[3-5]的缺点。另外,在户外使用的移动显示系统受强光照射时,图像饱和度降低,可视性较差。在这种情况下,色彩增强技术可改善图像的可视性。

显屏驱动芯片属于专用集成电路(Application Specific Integrated Circuit,ASIC),不带有处理器核。因此,应用于显屏驱动芯片的色彩增强算法要求运算简单、计算速度快、占用存储空间少,便于以数字电路形式实现。显然,一些已经开发出来、应用于电视、摄像机、计算机等产品的色彩增强技术[6-13]因算法复杂、需借用软件系统实现,而不能应用于显屏驱动芯片。近十多年来,适用于显屏驱动芯片的色彩增强技术被研究和开发。Lai 和Tsai 等[3-4]提出一种基于特别构造的线性变换矩阵的色彩增强方法(被称为Rich Color 法),由于其实现的简便性而被芯片设计商采用,成为主流的色彩增强方法。罗宁[14]提出色彩矢量概念,并基于此提出一个本质上属于颜色空间线性变换的色彩增强专利,但并未提供实现的所有细节。这两种技术具有逐像素处理、计算简单、硬件资源耗用少的特点,但对色彩增强程度无法进行参数化调节,对增强效果也无法准确预知,从而不便于主控芯片对增强过程进行调控。

为解决现有技术存在的上述问题,提出了一种新的对增强效果可进行精确调控的图像色彩增强算法(直方图分析法)。它不仅具有计算简捷的优点,而且通过预设饱和度增高系数这一参数,实现了对色彩增强效果的直接调节。进一步地,为防止出现饱和度数值饱和的像素过多而引起图像质量下降,通过对每幅图像的饱和度进行直方图的分析,计算最大许用饱和度增高系数,并最终得到适合于该图像的实际饱和度增高系数。本文对所提出算法的效果进行了测试,并对所需的计算资源进行了评估。结果表明,该算法不仅色彩增强效果良好,而且计算资源耗用较少,适合用于显屏驱动芯片领域。

1 可精确调控的色彩增强方法

众所周知,在HSV 色彩空间中,饱和度S是表达像素色彩艳丽程度的参量。因此,提高像素饱和度是色彩增强的有效手段。本文所提出的色彩增强方法也以此为基础。为使计算简便,并使各像素饱和度之间原有的比例关系保持不变,在该方法中,各像素采用相同的饱和度增高倍数。作为调节参数,将主控芯片发送的预期增高倍数称为预设饱和度增高系数(记为k0)。

为便于应用电路进行计算,将S量化为8 bit 整数,故其取值范围为[0,255]。在S增大过程中,原本饱和度较高的像素可能发生饱和度数值超过255而被截止为255 的现象(即数值饱和),从而引起图像质量降低。为将图像质量降低程度控制在可接受范围内,需设置像素截止率阈值(设为r),使发生截止的像素占比不大于r。为此,对于不同的图像而言,需要对其像素饱和度数值的分布进行分析,以计算满足截止率阈值条件的最大许用饱和度增高系数(设为k1)。最后取k0和k1之间的较小值,作为实际饱和度增高系数(设为k)。通过这种方式,使算法既具有参数可调节性,又可对图像质量进行控制,确保了算法的有效性。

1.1 RGB 空间与HSV 空间的相互转换

如前文所述,本文所提出的色彩增强方法需借助HSV 颜色空间[15-16]予以实现。为此,需根据图像像素R、G、B颜色值计算色相(hue,H)、饱和度(saturation,S)和明度(value,V)(如图1 所示)。假设R、G、B数值区间为[0,255],上述计算过程可由式(1)至式(7)的一组公式表示:

图1 HSV 颜色空间模型

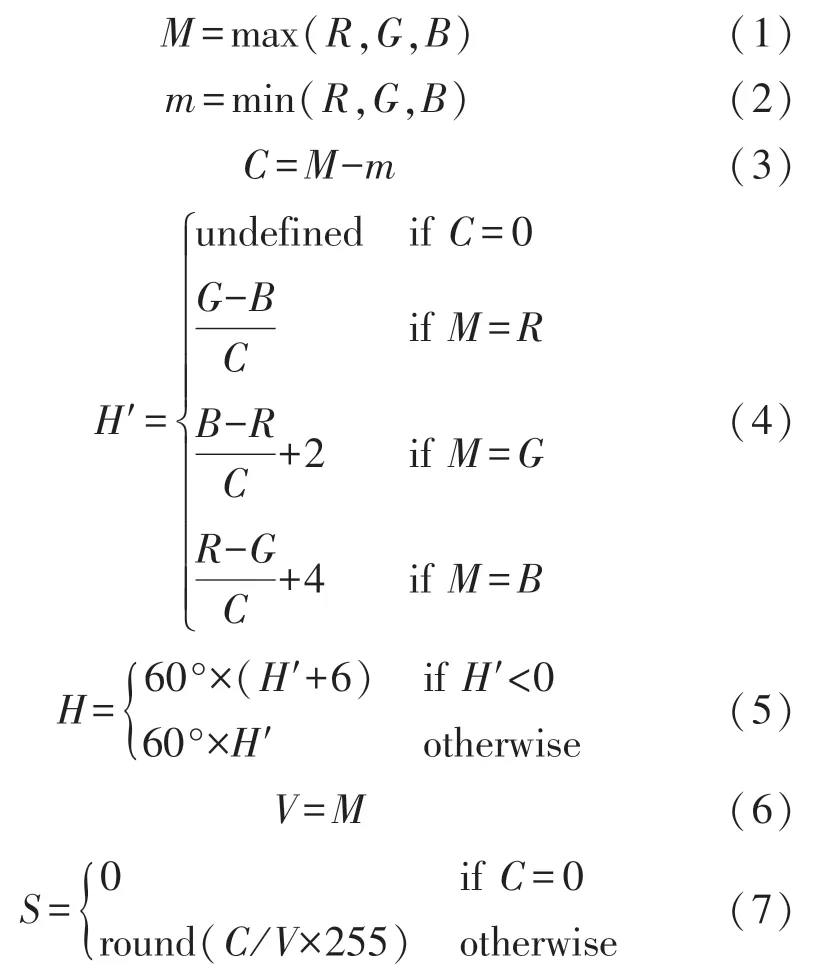
根据HSV 模型,色调H反映了颜色在色盘中所处的角度。在本文提出的算法中,为了防止图像发生色偏,将各像素的色调保持不变。为便于计算,引入如下与H相关的量:

式中:d为像素R、G、B三个颜色值中除M、m之外的中间值,即m≤d≤M。显然,对于同一像素,色调保持不变即意味着Hp保持不变,因此式(4)、(5)的计算可由式(8)替代。在保持Hp不变的同时,本文算法保持m、d、M与R、G、B之间的对应关系始终不变。

引入Hp参量后,从HSV 空间到RGB 空间的转换公式也得到简化。当色彩增强过程中像素的S和V值被更新后,可由以下公式计算m、d、M的更新值:

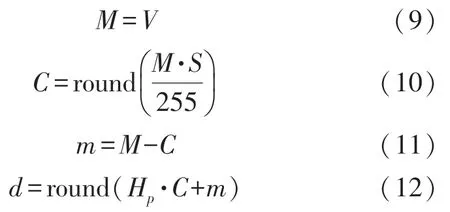
根据m、d、M的更新值以及它们与R、G、B之间的对应关系,即可得到增强后像素的颜色值(R′、G′、B′),从而完成从HSV 空间到RGB 空间的转换。

1.2 最大许用饱和度增高系数的计算

如前文所述,在一定的饱和度截止率r条件下,对于具有不同饱和度分布的图像,其饱和度可提升的程度可能不同。通过对特定图像饱和度直方图的分析,可计算出该图像的最大许用饱和度增高系数。步骤如下:

(1)计算图像的饱和度直方图数组h(S),S＝0,1,…,255。h(S)表示饱和度等于S的像素个数。

(2)按L＝255,254,…,1,0 的顺序计算累积数组A(L),直至A(L)＞N·r时停止(N为像素总数),记录此时L的值。其中A(255)＝h(255),A(L)递推公式为:A(L)＝A(L＋1)＋h(L)。

(3)计算最大许用饱和度增高系数k1。若L＝0,则令k1＝1；否则,令

图2、图3 所示为色彩增强的一个实例。图3(a)为图2(a)所示原始图片的饱和度直方图。在r＝0.05 条件下,计算得L＝202,k1≈1.262。图2(b)为图2(a)在饱和度增高k1倍后的效果图(像素亮度遵循变化最小准则),图3(b)为图2(b)的饱和度直方图。显然,经过色彩增强后,饱和度直方图整体向S轴正方向扩展。

图2 色彩增强实例(N＝76 800，r＝0.05，k1≈1.262)

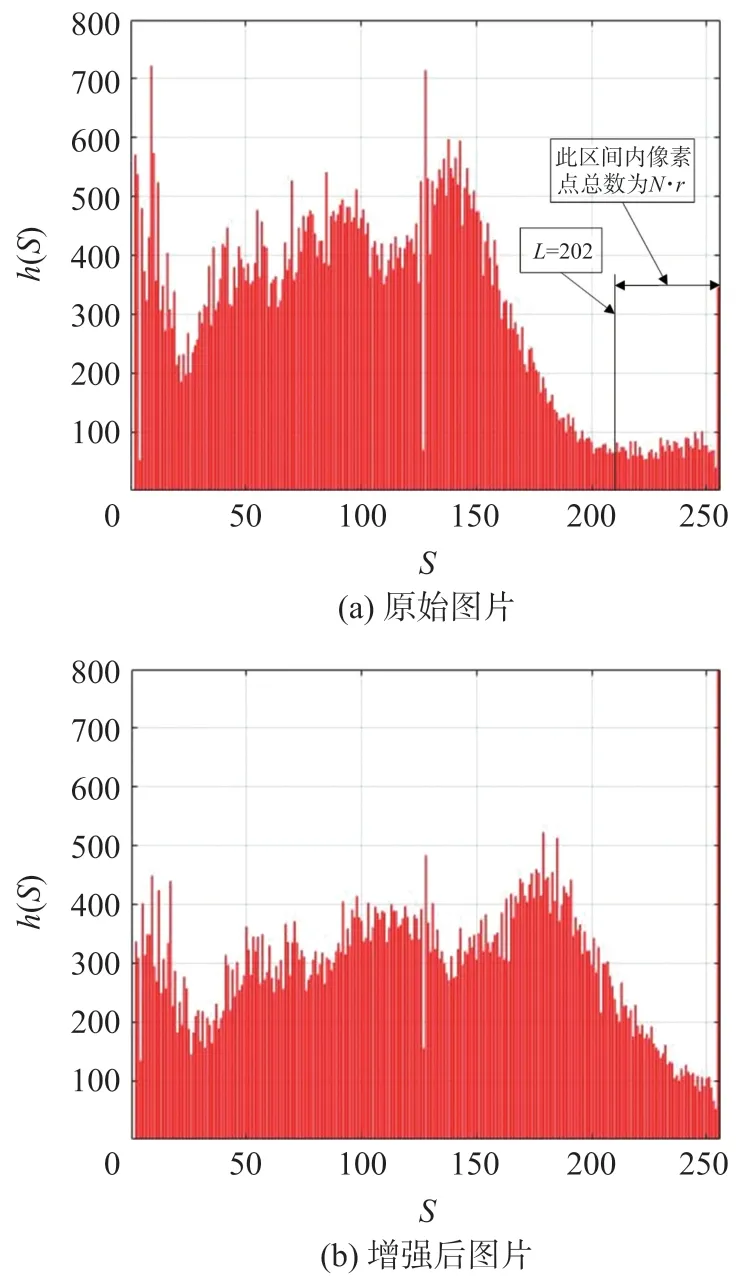
图3 图2 中图片的饱和度直方图

得到k1之后,取k＝min(k0,k1)。对于图像的每个像素,增强后的饱和度为

1.3 最小像素亮度变化准则

饱和度增高的过程可能引起像素亮度的改变,从而改变图像原有的视觉效果。这对色彩增强算法的应用是不利的。因此,有必要在算法中增加“最小像素亮度变化”这一准则作为约束条件。鉴于YCbCr颜色空间的Y分量被广泛用于图像亮度表达,在本文提出的算法中也采用该参量计算像素的亮度。

由RGB 空间颜色值计算亮度Y的公式如下[3]:

根据式(1)～(8),将式(15)改写为

上式中系数wm、wd、wM的值根据该像素m、d、M与R、G、B之间的对应关系选取。

为进一步利用最小像素亮度变化准则,现推导Y与M的关系。不妨忽略公式中的圆整操作,由式(10)、(11)可得

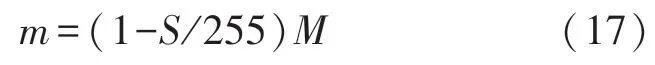
由式(8)可得d＝Hp(M-m)＋m,将式(17)代入并化简,得

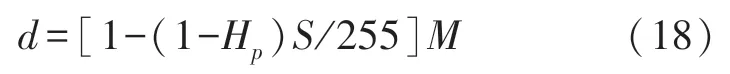
将式(17)、(18)代入式(16),并利用关系式wm＋wd＋wM＝1,化简得

假设经过色彩增强,像素颜色值由(R,G,B)变为(R′,G′,B′),相应地(m,d,M)变为(m′,d′,M′)。设理想情况下像素亮度保持Y不变,根据式(19)和新饱和度值S′,得M′在此理想情况下的值为

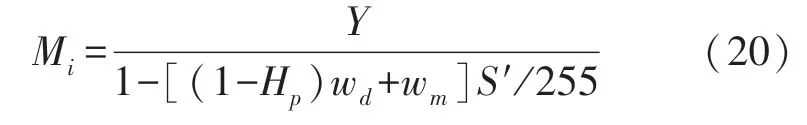
由于0≤Hp≤1,可得Mi≥0。另一方面,Mi可能超出255。为防止数值溢出,取

得到M′以后,根据式(17)、(18),应用新饱和度值S′,可分别算出m′、d′。由于m′、d′、M′与R′、G′、B′之间对应关系保持不变,即可得到增强后的R′、G′、B′值。式(9)～(12)所示的空间转换计算实际上被隐含在上述求解过程中。

1.4 算法的总体流程

前文分析了色彩增强的计算过程,它可分为图像分析和增强计算两个阶段。在第一阶段包括图像像素颜色空间转换、图像饱和度直方图计算、最大饱和度增高系数计算、实际饱和度增高系数选定等操作。第二阶段的任务是在第一阶段分析结果的基础上,逐像素地进行色彩增强操作。图4 为该色彩增强算法流程图。

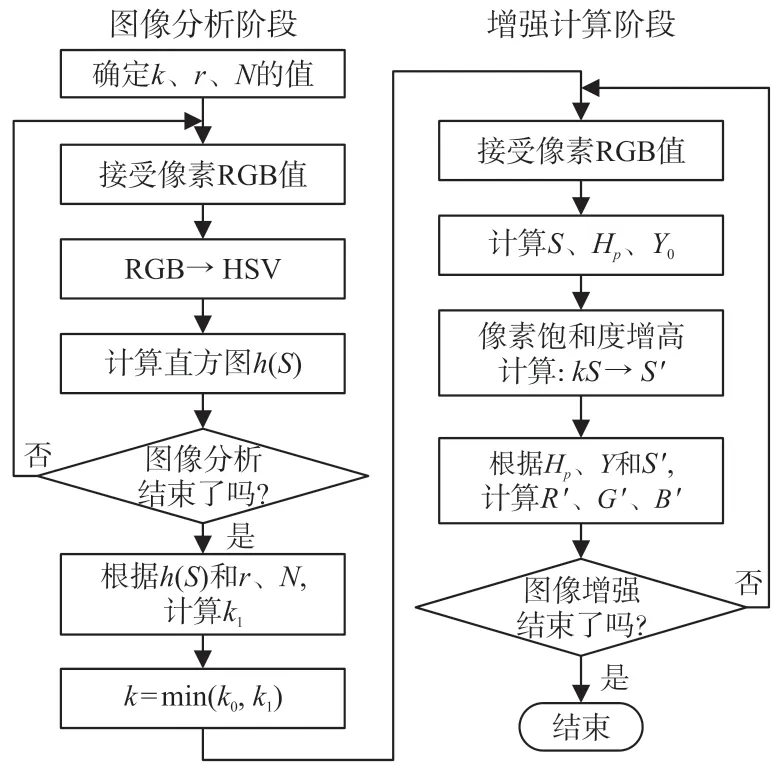
图4 色彩增强算法流程图

2 算法测试结果及讨论

2.1 对直方图分析法的测试

本文对所提出的色彩增强方法——直方图分析法,进行了大量的实验测试。实验选用的图片包括自然景物照片、人像图片、卡通图片、手机操作界面等。实验结果表明,本文所提出的方法有效。借助于参数k0和r,算法可以对色彩增强效果进行精确的调控。k1则反映了算法对图片内容的自适应能力:在r值允许的前提下提供最大的饱和度增高倍数。当k＝k0时,系统按照主控芯片的指令进行增强操作；当k＝k1时,系统虽然没达到主控芯片指令(k0)的要求,但在保证图像质量的前提下实现了增强效果最大化。因此,该算法兼顾了图像质量和增强效果两方面的要求。

显然,当k0和r增大时,色彩增强效果将会提高,但图像质量下降的风险变大,主要表现为图像局部饱和度过高而丢失细节。大量测试结果表明,当1≤k0≤1.5 并且0＜r≤0.05 时,增强效果较好且图像质量无明显下降,因此这是k0和r优先选择的范围。

图5、图6 所示为采用直方图分析法对“小鸟”图片进行色彩增强的实例。在此例中,r＝0.05。计算得到k1＝1.308。当k0分别取1.1、1.2 和1.3 时,均得到k＝k0。

图5 小鸟图片色彩增强实例(r＝0.05)

图6 “小鸟”图片的饱和度直方图

在色彩增强算法中,图像色彩增强的效果常采用CIE1931 空间的色域图大小变化进行评估[3-4]。图7 为“小鸟”图片色彩增强前后的色域图。在基于饱和度调节的色彩增强算法中,饱和度为零的灰色像素在色域上的位置是保持不变的。由此,选取亮度最大的白色像素在色域上的对应点作为基准点,计算图像色域所有像素至该基准点的平均距离D。显然,D可作为色域大小的评价指标。设原始图像和增强后图像色域像素到基准点的平均距离分别为Di和De,定义色域扩展系数如下:

图7 “小鸟”图片的色域

表1 列出了“小鸟”图片增强后的色域扩展系数。从该表可见,色域扩展系数随着k增大而增大。这说明本文提出的色彩增强算法是有效的,并且能够对增强效果进行精确调控。

表1 “小鸟”图片增强后的色域扩展系数

2.2 与Rich Color 法的比较

本文所提出的直方图分析法在以下两方面优于Rich Color 法:(1)前者可利用参数k,对色彩增强效果进行调节；而后者的增强效果依赖调节因子s的取值,而其取值由经验数据决定,不便于调节。(2)前者可保持图像质量基本不变,而后者关于s的表格数据平滑性不好,对于颜色缓变的图片可能产生不期望的条纹,从而导致图像质量下降。对第(2)点,举例说明如下。

构造一个点阵为179×128 的颜色缓变图像,其中每个像素的G分量均为240。每一行像素颜色值相同,并且R和B分量相等。第1 行像素R和B分量的值为42,此后逐行加1,直至第240 行R和B等于220,如图8(a)所示。图8(b)所示为采用本文所提出直方图分析法得到的增强效果,由于其各像素饱和度增高系数相同,因而其颜色保持了平滑缓变的效果。图8(c)所示为采用Rich Color 法得到的增强效果,其上部区域出现了明显的条纹,图像质量较差。

图8 颜色缓变图增强效果对比

3 硬件实现方案及资源评估

3.1 硬件系统模块图

如前文所述,本文所提出的色彩增强方法面向显屏驱动芯片应用,以电路形式实现。随着平面显示器分辨率不断提高,其驱动芯片为了节省成本,逐渐以“无帧存储器(RAMless)”的设计为主流方案。这要求色彩增强算法在图像传输的同时完成所有计算。图9 为满足此要求的色彩增强系统模块图。在此系统中,由于直方图分析模块需要在一帧图像传输结束后,才能输出该帧图像的k值,因此该值在饱和度增高计算中的应用将延迟一个帧传输周期(如图10 所示)。

图9 色彩增强系统模块图

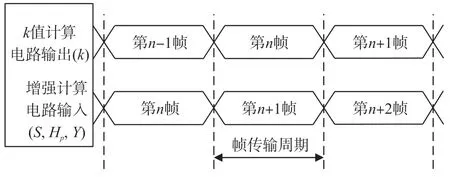
图10 色彩增强系统内部时序示意图

由于主流平面显示器刷新频率为60 frame/s,而所显示图像和视频处于静止状态或相对而言变化较慢,因此上述的k值延迟不会对图像色彩增强效果带来明显负面影响。通过在平板电脑、智能手机上对有k值延迟和无k值延迟两种视频的对比实验,二者无明显差别。

3.2 硬件资源耗用评估

本文所提出的算法运算简单,其所耗用的硬件资源也较少(参见图9),主要由RGB 与HSV 空间转换计算电路、直方图分析电路和存储器三大部分组成。RGB 至HSV 和HSV 至RGB 转换计算均需用到除法运算。由于硬件除法器不仅计算耗时,而且需要较多硬件资源,故在进行电路设计时,将所有除法转化为乘法运算,即乘以除数的倒数。为此,建立了一个长为255 byte 的倒数表,存放在只读存储器(ROM)中。直方图数据字长为16 bit,储存于随机存取存储器(RAM)中。由于实际应用中一般k＜2,128≤L≤255,因此直方图数组h(S)只需128 项,RAM 空间选取128 Word 即可。控制参数r、k0、k1、k等以及其他中间变量字长为8 bit,存储于18 个寄存器中。表2 为该系统存储空间统计表。

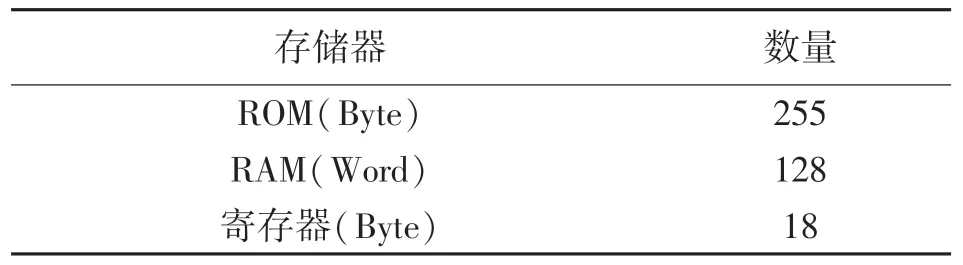
表2 系统存储空间统计表

4 结论

本文面向显屏驱动芯片应用,提出了一种图像色彩增强方法,其中包括饱和度直方图分析、RGB与HSV 颜色空间之间的快速转换等步骤。该方法突出的优点是,在确保图像质量的前提下,可对增强效果进行精确的调控,便于主控芯片对该功能的使用和控制。同时,它运算简便,耗用硬件资源少,便于以算法模块的形式在各种显屏驱动芯片中应用,以增强产品的功能和竞争力。