弹性变径管对于内流振动影响的仿真研究
宋彦宏,张天翔,马 李,陈有权
(1.吉林大学 机械与航空航天学院,吉林 长春 130025; 2.兰州大学 土木工程与力学学院,甘肃 兰州 730000; 3.长春理工大学 机电工程学院,吉林 长春 130022; 4.吉林大学 通信工程学院,吉林 长春 130012; 5.长春工业大学 人文信息学院机械工程系,吉林 长春 130122)
1 引 言
管道在传输能量和流体介质时,通过内流作用,也传递振动和噪声。 多工况液压流体管路振动严重,并伴有强烈的共鸣声。 在工况突然改变时,往往会导致水击现象。 多年来,研究者对气液两相流水击通径直管道进行了大量的研究,着重研究了两相流水击的产生、强度和传播规律以及含气率对水击压力、传播速度的影响。 目前,直管道两相水击的基本理论体系已经建立[1-3]。 实际上,管道系统除直管外,还存在弯头、变径等附件[4],本研究将对变径的水击过程进行分析。 水击波在非通径管道中传播时,壁面的反射和管道与流体的耦合作用会产生复杂的波动过程。 迄今为止对管道系统水击问题的研究,通常是将实际的非通径管道用现有的一维瞬变流直通径管理论进行计算分析[5]。 王树立等[6]通过试验对气液两相流水击波在弯管中的传播进行研究, 揭示了水击在弯管道中的传播规律及压力分布,同时水击压力在弯管外测大、内侧小且形成压力环,压力环形状衰减过程与含气率有关。近年来,大多数研究者对变径腐蚀、加工、流变振动进行了相应研究[7-10],但对直管变径的水击分布冲击、噪声理论模型及关键影响因素的探析很少有人涉及。 水管网的内流振动会严重降低薄弱原件和隔膜阀寿命[4],增加噪声,严重时造成爆管、管路支撑破坏、液压系统失效。 例如,潜艇的水平舵液压管道内流振动作为主要的噪声来源,严重的噪声会影响声呐检测距离和效果,降低潜艇的隐蔽性[11]。 本研究主要针对变径的内流振动特性和关键影响因素进行分析,其成果可用来指导变径用于多工况液压管网设计。
2 变径的振动数学模型
对于管道中的一种可以压缩的在x方向流动的水流,将水管作为一维问题来研究,其动量方程为
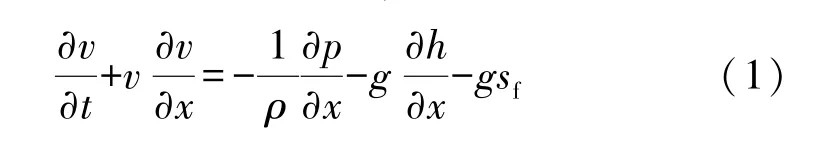
式中:v为流速;x为水流在管道x方向的位置;p为水的压力强度;ρ为水的密度;h为管道的高程;sf为摩擦坡降;g为重力加速度。
根据质量守恒可得,考虑相隔dx的两个横截面之间的空间,净的流入该空间的质量必须等于该空间内部质量的增值:

初始条件为:t=0、y=0、dy/dt=v0/N。 于是,无摩擦阻力的管道水头为

3 变径的振动AMESim 仿真
AMESim 仿真的一大优势就是其建模仿真的图形化。 利用复杂多学科、多领域系统建模仿真平台,主要运用Hydraulic Component Design 库和Hydraulic 库中的基本元件[12],构建变径AMESim 仿真模型(见图1,其中A 表示变径接头正接(前大后小)、B 表示变径接头反接(前小后大))。
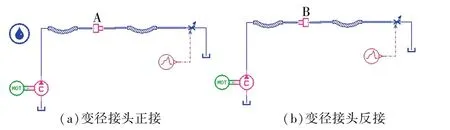
图1 变径AMESim 仿真模型
通过仿真得出图2 所示结果,由此看出变径大端(红色曲线)的压力波动和静压力均低于变径小端(绿色曲线),变径可以作为液压管道的减振滤波器。
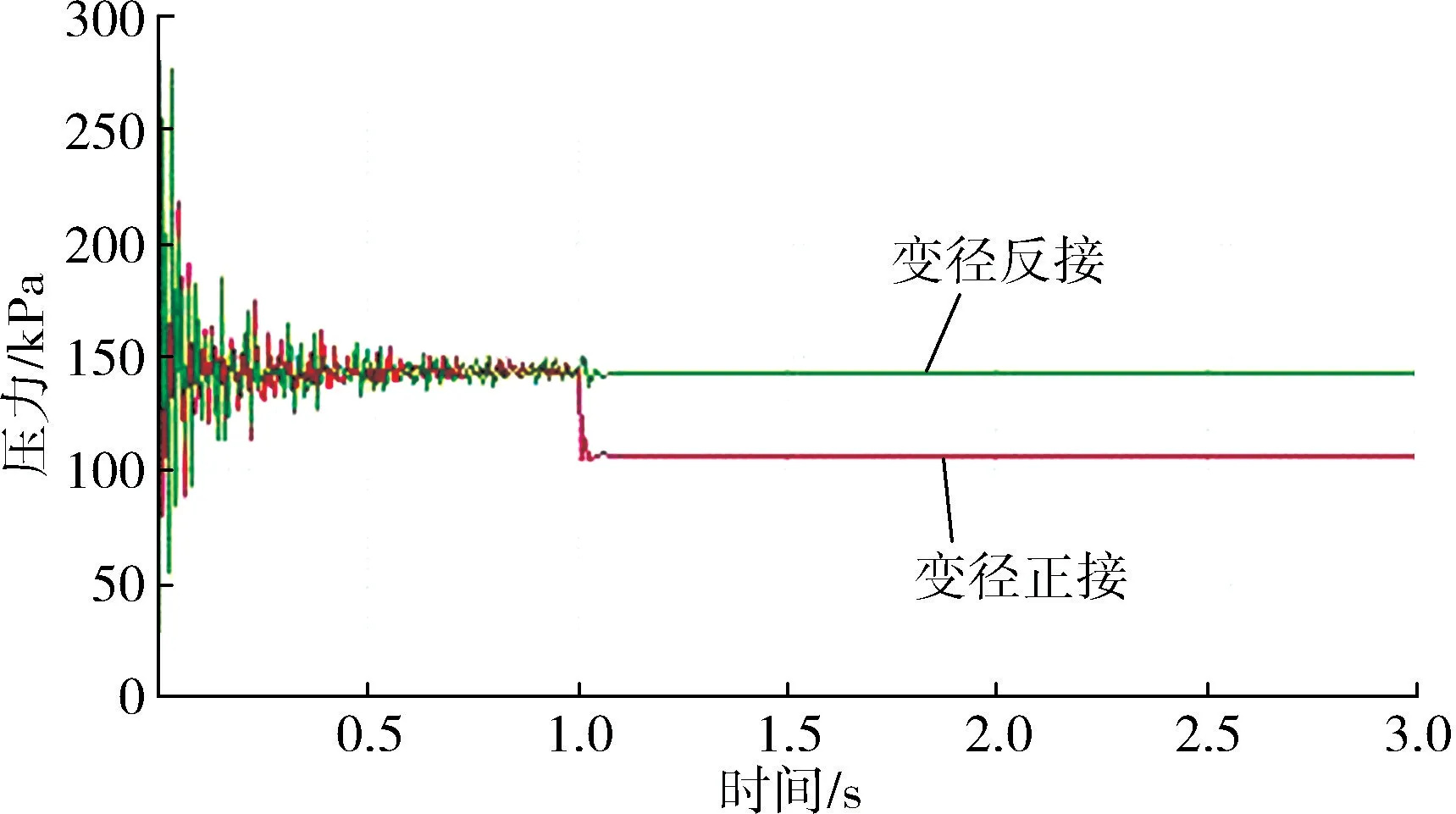
图2 变径大端与小端的压力波动对比
4 基于Modelica 的物理统一建模与仿真
基于Modelica 语 言[13]的MWorks © 2019 平 台(华中科技大学CAD 中心研发的面向多领域工业产品的系统级综合设计与仿真验证平台)对变径进行数值模拟,它具有多物理场、多变量、多目标、多约束优化的优势。 根据实际参数对变径数学模型进行数值求解,通过多目标统一建模,内置IPOPT(Internal Point OPTimzer)优化算法求解,实现多目标的非线性优化求解。 如图3 所示为无变径和变径比为1 ∶5 的线性摩阻振动分布,显然变径会在0~600 s 内降低末端振动,降低噪声。 在管网设计时,合理利用变径会削弱管道摩阻对水击振动的影响。
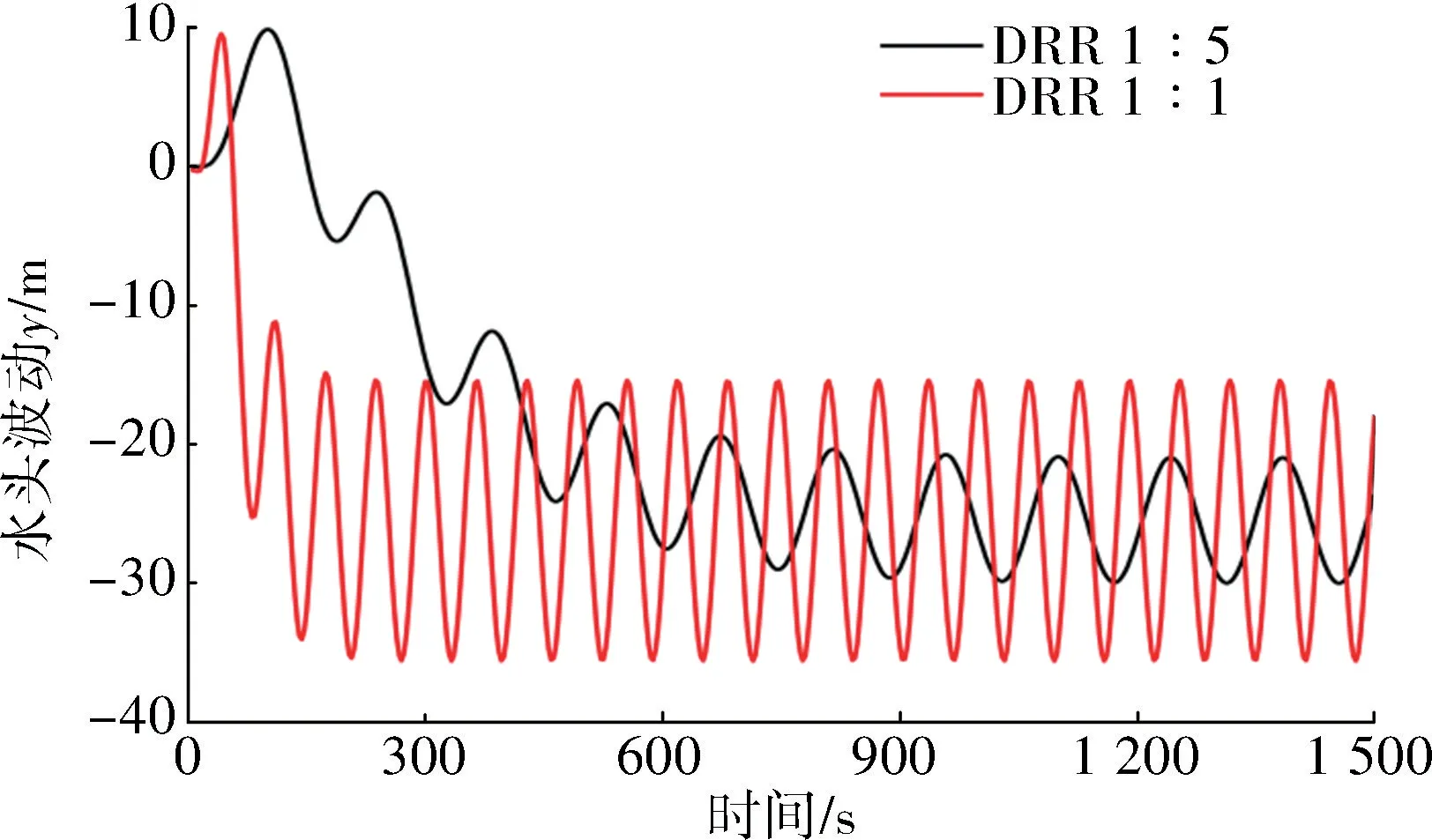
图3 DRR 为1 ∶1、1 ∶5 的线性摩阻振动对比
下面探究变径的影响因素:改变变径比对长管道脉动[14]产生影响,变径比越大影响程度越大(见图4);变径的长度对长管道振动几乎不产生影响,只是推迟振动相位(见图5);湍流状态管道介质流速越大,对长管道振动摩阻影响越大(见图6)。
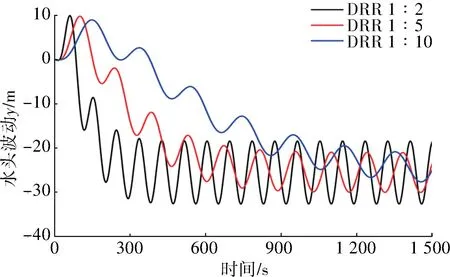
图4 DRR 为1 ∶2、1 ∶5、1 ∶10 线性摩阻振动影响
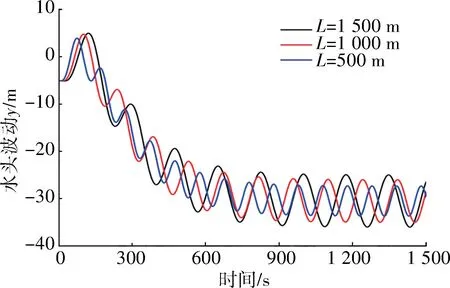
图5 DRR 为1 ∶5、变径长度为500~1 500 m 线性摩阻振动影响
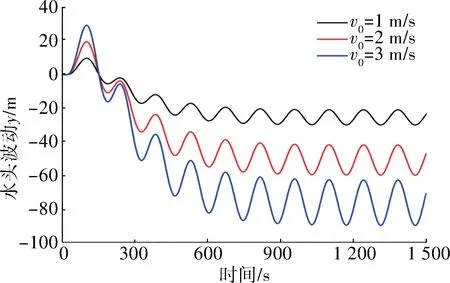
图6 DRR 为1 ∶5、末端流速为1~3 m/s 线性摩阻振动影响
对于线性摩阻的湍流长管道,改变变径比会对长管道振动分布产生影响,变径比越大改善程度越大(见图7)。
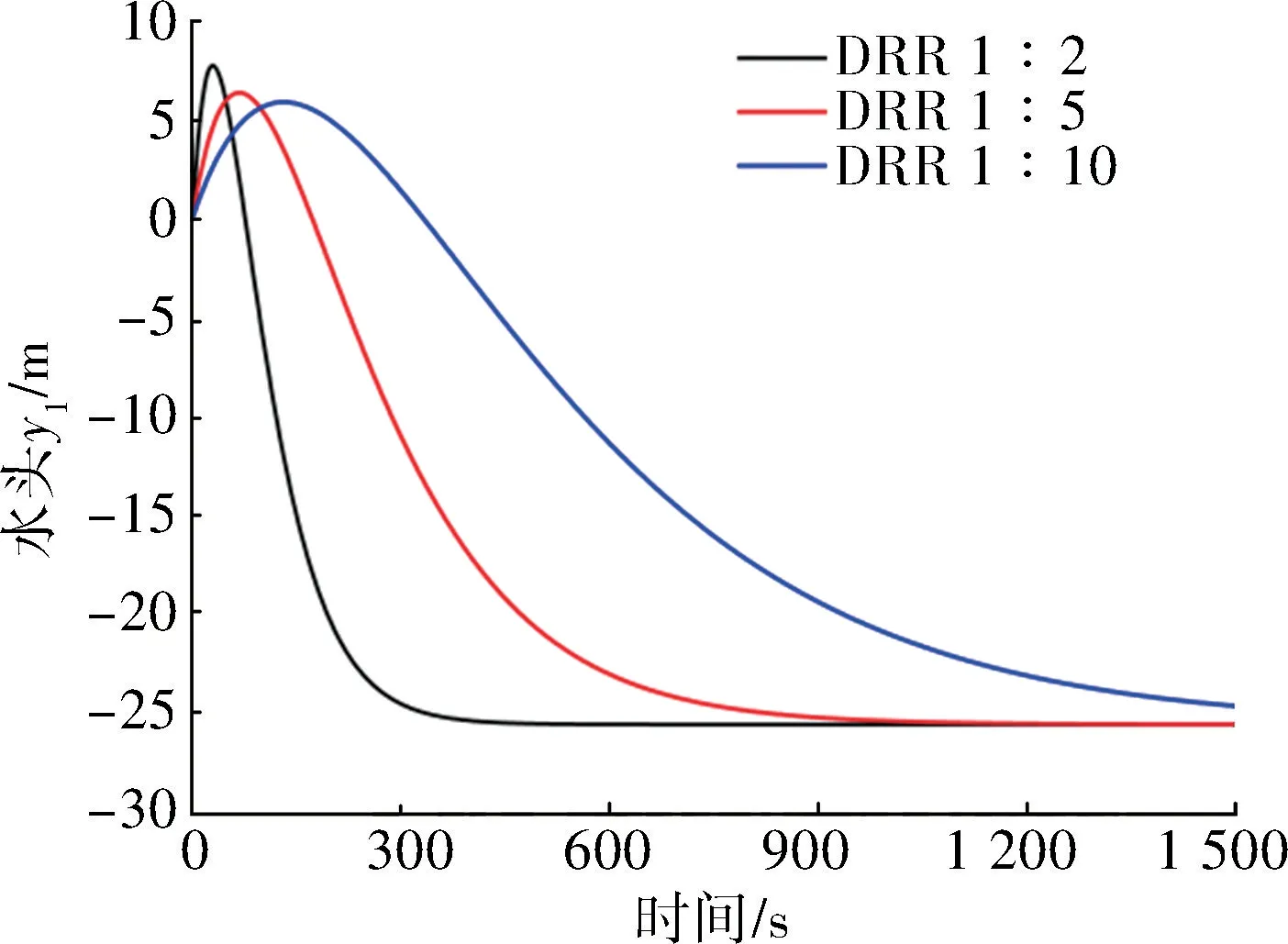
图7 DRR 为1 ∶2、1 ∶5、1 ∶10 的线性摩阻振动分布
对于线性摩阻的湍流长管道,在变径比为1 ∶5 的变径作用下,介质波转移速度越大对长管道振动分布的影响越严重,介质波转移速度越大振幅越大(见图8)。 介质波速低表明液体含气量多,介质微粒存在缓冲,能量耗散大,介质水容积模数低,介质的可压缩性大。
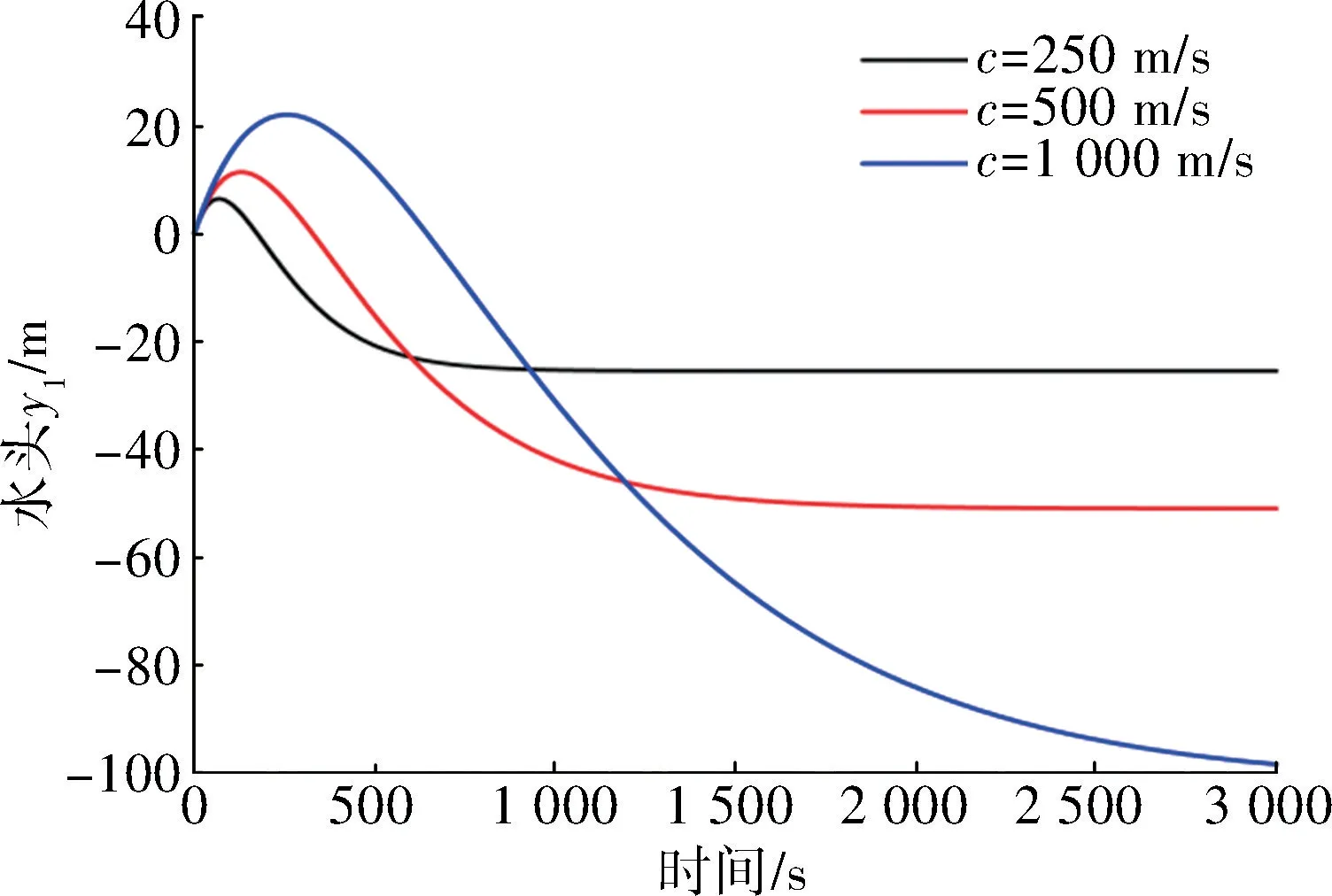
图8 DRR 为1 ∶5、介质波速250~1 000 m/s 线性摩阻振动分布
5 降噪变径的设计与性能验证
在管道设计时,为了减振降噪,试验中设计了一款隔层十字花节流孔,通过CFD 流场分析得到流速、压力和流线分布。 本研究设计出由小直径段、大直径段和十字花变径隔层3 部分构成的旋流节流孔(见图9)。
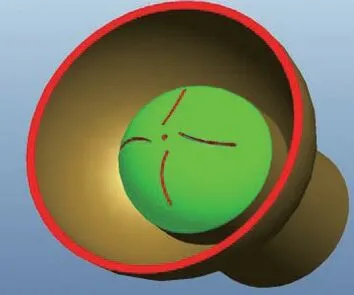
图9 十字花节流孔
小直径段上应该设计卡槽直接与其他元件相连,大直径段是图9 中所示的带红边的半球形液流罩,这里的大容腔会降低振动频率,从而降低噪声源的噪声;十字花变径隔层由中心泄流孔和4 条旋流缝隙构成。中心泄流孔的作用是泄流,防止液流流出时憋压,4 条旋流缝隙目的是为了实现液流的涡流和旋流。
为了研究该变径的内部流动情况,进行了CFD 流场仿真,设置初始条件:速度入口,流速为1 m/s;压力出口,压力设为0.01 MPa。 经过CFD 流场仿真得出降噪变径节流口速度场分布(见图10),速度的最大值为25.6 m/s、最小值为1.0 m/s。 从图10 中可以看出节流孔出现了旋流涡,这会增加能量耗散,降低介质波速,从而降低振动幅值。
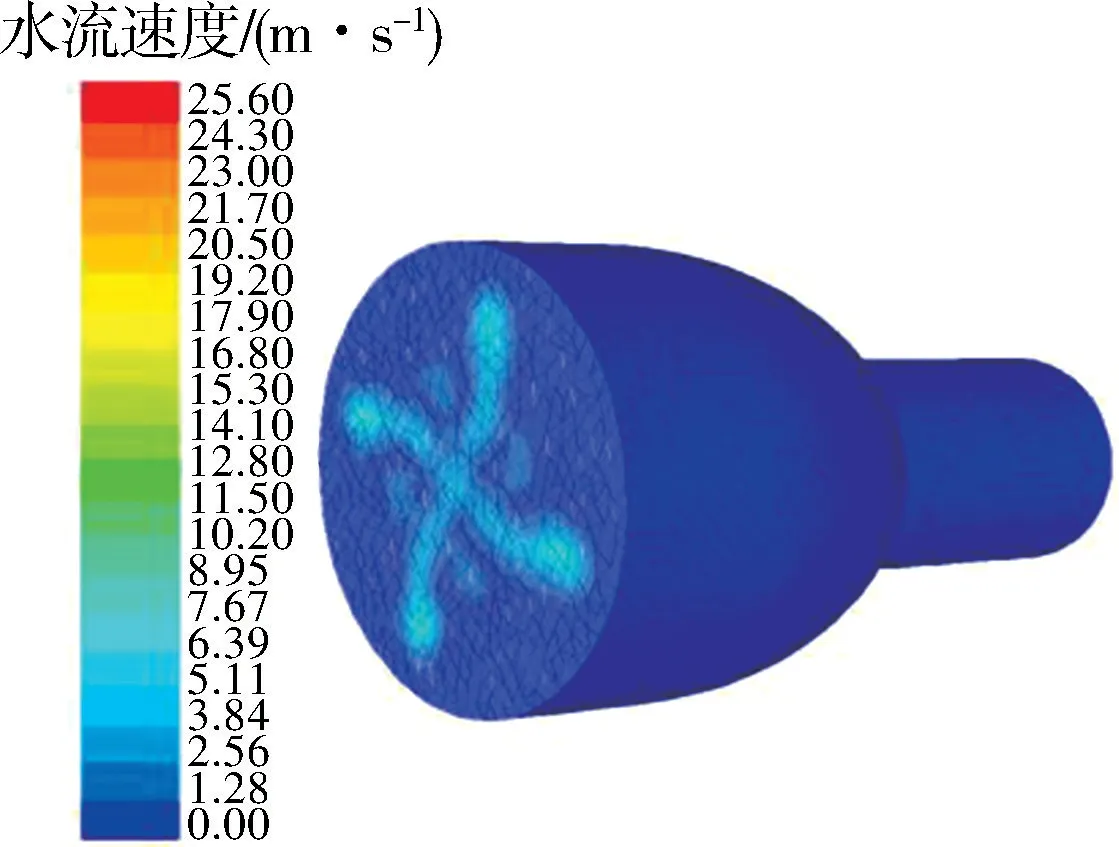
图10 十字花节流孔的整体标量速度场分布
经过CFD 流场仿真得出降噪变径节流口流线分布(见图11)。 从图11 中可以看出液体流线杂乱程度高,能量耗散严重,变径大端有利于实现减振降噪。
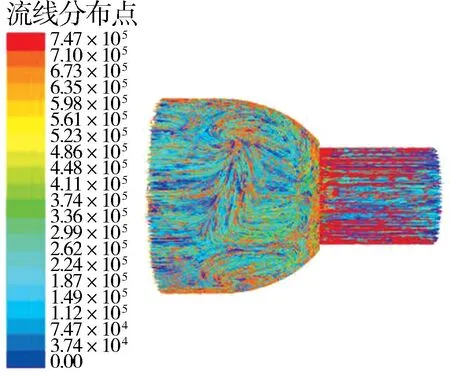
图11 十字花节流孔的整体流线分布
6 结 论
本文首先把管道流抽象为一维流体流动,建立变径的水力分布数学模型;其次,通过AMEsim 仿真平台建立变径液压管路模型,得出变径在液压系统中不但可以作为连接元件,还可作为一个多频滤波器,可以降噪减振;然后,通过基于Modelica 语言的MWorks 平台,对变径的压力、水力分布数学模型进行仿真;最后,我们设计了一款隔层十字花减振降噪节流孔,并通过CFD 流场分析得到其流速和流线分布,从而得出以下结论:
(1)弹性变径管的小径长度对振动分布影响不大,对波动相位影响大。
(2)变径比与介质流速对液流突变振动影响较大,变径比越大,水击振动改善效果越好;介质流速越小,噪声和冲击越小。
(3)介质波转移速度逐渐增大,水击传播速度滞后,这是因为介质波速增大,内摩擦也随之增大。
(4)通过合理匹配节流孔、设计节流孔格栅,会降低水击振动噪声;再通过CFD 仿真验证了其设计性能,变径十字花变径隔层造成的载流子旋流碰撞大大消耗振动能量,变径大端的大容腔从而降低振动频率,降低噪声源的噪声。
因此,管道设计中合理匹配变径可使得液压管网得到有效改进。

