圆柱体径向劈拉法检测橡胶混凝土抗拉强度试验研究

马 莹，袁 群，冯凌云，刘春丽，秦世兵

（1.河南省水利科学研究院，河南 郑州 450003；2.河南省科达水利勘测设计有限公司，河南 郑州 450003；3.河南省水利工程安全技术重点实验室，河南郑州 450003；4.华北水利水电大学地球科学与工程学院，河南郑州 450046；5.河南省水利勘测设计研究有限公司，河南 郑州 450016；6.新乡市水利科技推广中心，河南 新乡 453001）

1 引 言

混凝土的抗拉强度远低于其抗压强度，因此混凝土裂缝在受拉作用下易发生扩展，影响混凝土的使用寿命和耐久性［1］。 在GB／T 50081—2002［2］中列出了立方体劈拉法（即劈裂抗拉试验法）和圆柱体劈裂法（即巴西劈裂法）2 种混凝土抗拉强度测定方法。 以往的研究表明，从巴西劈裂法获得的混凝土抗拉强度比梁弯曲试验更接近真实的抗拉强度，由此证明巴西劈裂法比立方体劈拉法能提供更好的抗拉强度预测［3］。

当使用巴西劈裂法测量混凝土的抗拉强度时，会遇到以下限制：①在混凝土结构上钻孔取得的圆柱体芯样长度不等且端面多不平整，因此在测试之前，圆柱体芯样必须以高径比为2 进行处理。 ②抗拉强度数据较少，每个圆柱体芯样只能取得一个抗拉强度值，且混凝土结构因钻孔损伤而可取得的芯样数量有限。 ③获得完整的混凝土芯样需要具备良好的工作环境和熟练的技能，否则难以取得理想的完整芯样。 为了改善这种情况，袁群等［4］提出了圆柱体径向劈拉法来测试混凝土抗拉强度。 与巴西劈裂法不同的是，圆柱体径向劈拉法的荷载是在圆柱体截面直径方向上施加的。 圆柱体径向劈拉法具有以下优点：①增加了抗拉强度数据量（混凝土圆柱体试件可多次劈裂）；②减少混凝土芯样的处理程序（混凝土芯样的端面不需要切割找平）；③提高混凝土芯样的使用效率（测试小于JGJ／T 384—2016［5］规定的最小长度的试件）。

余江滔等［6］、肖芳等［7］从理论上验证了圆柱体径向劈拉法的合理性。 袁群等［8］利用有限元模型分析了混凝土横断面应力分布的合理性，发现横断面的拉伸破坏取决于圆柱体的轴向拉应力。

虽然圆柱体横向劈裂法在试验、数理统计、有限元建模等方面证明是可行的，但仍难以采用合理的计算式确定圆柱体横向劈裂强度。 混凝土圆柱体径向劈拉强度在前人研究中［4］用名义横向劈裂强度P／A表示（P为破坏载荷；A为表面劈裂面积）。 在本研究中，混凝土圆柱体名义径向劈拉强度与立方体劈拉强度之间有很强的相关性。 通过对大量试验数据的回归分析，建立了用圆柱体径向劈拉法测试混凝土抗拉强度的计算公式；同时，混凝土试样除了普通混凝土，新增了橡胶混凝土，以扩大圆柱径向劈裂法的应用范围，探索更广泛的混凝土组成。

2 试验材料和方法

2.1 试验材料

本研究采用普通硅酸盐水泥42.5，其性能见表1。粗骨料为石灰石碎石，细骨料为天然河砂和1 ～3 mm、3～6 mm 的橡胶颗粒（通过破碎废轮胎得到的）。 粗骨料和细骨料的特性见表2。 橡胶颗粒的表观密度为1 119 kg／m3。 粗、细骨料指标分别满足GB／T 14684—2011、GB／T 14685—2011 中的要求。

表1 普通硅酸盐水泥42.5 性能指标

表2 粗骨料和细骨料的特性

2.2 配合比

试验混凝土使用了6 个水灰比（见表3）。 橡胶混凝土配合比是在普通混凝土配合比基础上，保持其他材料不变，用体积比例分别为1%、3%、5%、10%、15%的橡胶颗粒替代相应体积的砂（见表4）。 这些配合比基本涵盖了混凝土工程中常用的混凝土强度范围。

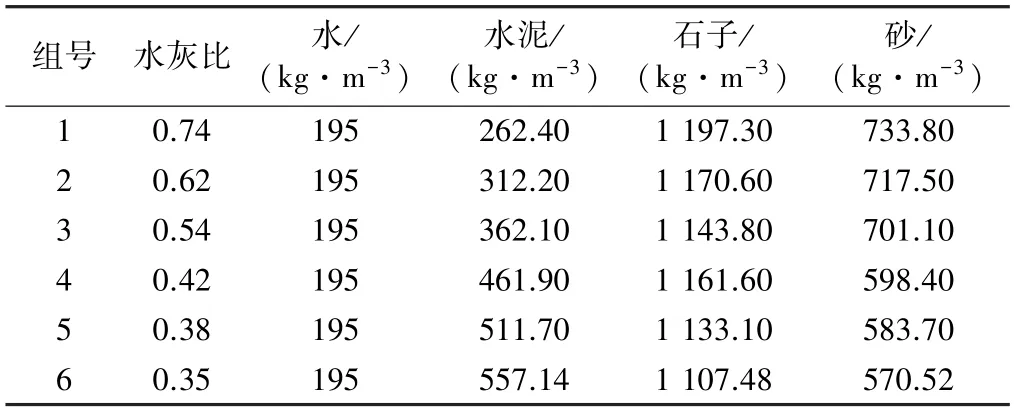
表3 普通混凝土配合比

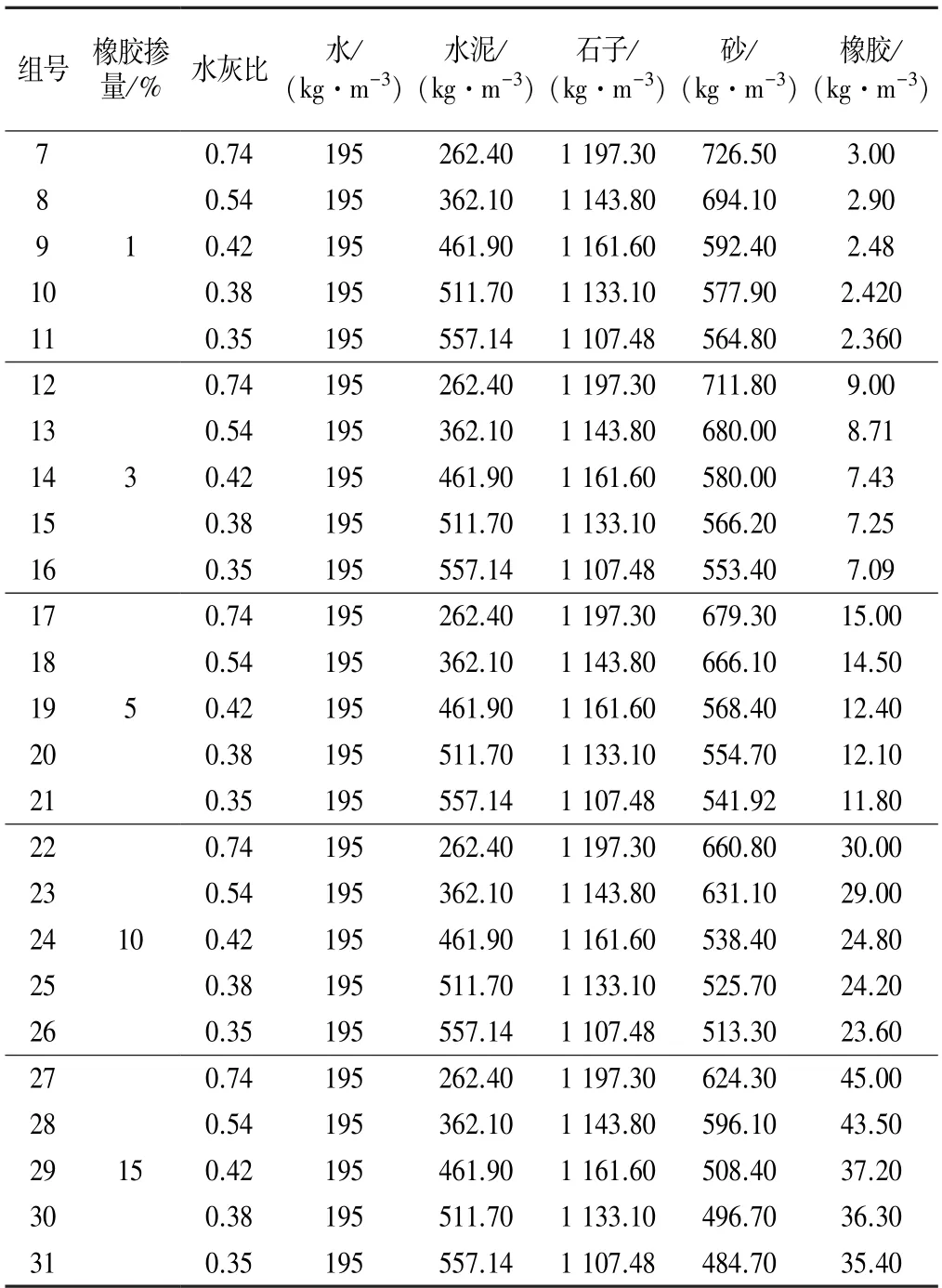
表4 橡胶混凝土配合比

2.3 混凝土试样

每种配合比混凝土包含立方体和圆柱体试样，试样根据SL 352—2020 制备，每组混凝土试样数量和尺寸见表5。

表5 每组混凝土试样数量与尺寸

2.4 试验方法

2.4.1 立方体劈拉试验

混凝土立方体劈拉试验按照规范SL 352—2020［9］进行。 试验仪器为液压万能试验机，最大试验力为2 000 kN。 为了对混凝土表面施加线性均布荷载，在混凝土表面和压板之间放置长度为200 mm 的方形钢条［10-12］，此时混凝土立方体劈拉强度按下式计算：

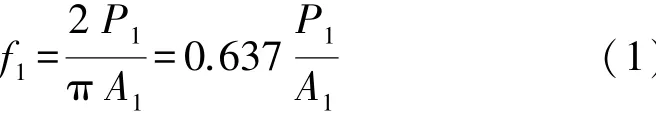
式中：f1为立方体劈拉强度，MPa；P1为破坏载荷，N；A1为横截面面积，mm2。

2.4.2 圆柱体径向劈拉法

圆柱体径向劈拉法使用的装置见图1。 使用液压伺服万能试验机的上、下压力板各1 块，测试仪器为液压万能试验机，最大试验力为1 000 kN。 与混凝土试件的接触位置为反弧型压力刀（其作用相当于立方体劈拉试验中的方形钢条），反弧型压力刀的压刀面宽为5 mm。

图1 混凝土圆柱体径向劈拉试验装置

圆柱体径向劈拉试验过程为：混凝土圆柱体试样在标准养护室中养护28 d，去除表面水分后立即进行测试。 用铅笔标记与试件横截面平行的周长，确定试样的劈拉位置（见图2）。 圆柱体试样的位移边界条件与圆柱体形状密切相关［13-15］，高径比是反映圆柱体试样特征的基本参数。 Yuan 等［16］发现当圆柱体高径比≥0.7时，径向劈拉破坏载荷随试件高度的增大变化不大，认为是稳定的。 因此，一个圆柱体试样可以均匀地劈拉3 次，在第1 次劈拉时高径比为2，在第2 次和第3 次分裂时高径比都为1。 试样按预定的劈拉位置对好放置在上、下压力刀之间，加载速率为0.04～0.06 MPa／s。

图2 混凝土圆柱体径向劈拉法劈拉位置

混凝土圆柱体名义径向劈拉强度定义为

式中：f2为圆柱体名义径向劈拉强度，MPa；P2为破坏载荷，N；A2为横截面面积，mm2。

3 试验结果分析

3.1 拉应力分布比较

立方体劈拉试验中，混凝土试件上、下表面中部施加均匀分布的压缩荷载（见图3（a））；压缩荷载使混凝土试件轴向面（与荷载同一平面）产生压应力，中部大部分区域产生均匀拉应力（见图3（b））；截面在拉应力作用下发生破坏（见图3（c））。 圆柱体径向劈拉试验与立方体劈拉试验的不同之处在于圆柱体试件沿圆周在截面曲线上均匀加载（见图4（a）），加载方向为截面直径方向；ANSYS 应力分析结果表明，混凝土试样中心区域大部分处于拉应力状态，影响了混凝土的抗拉强度（见图4（b））；试验破坏形态与应力分析结果较为一致（见图4（c）），说明圆柱体径向劈拉试验可有效地测量混凝土抗拉强度。

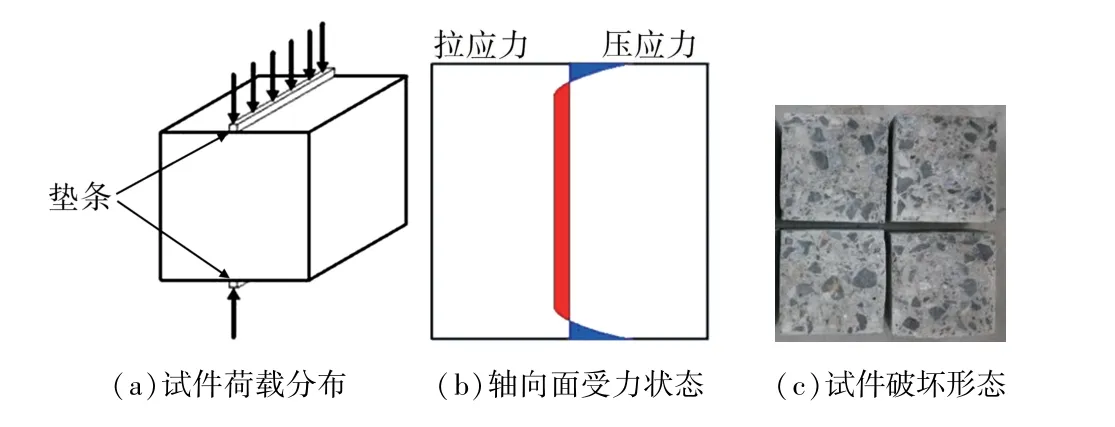
图3 立方体劈拉法的应力分布与试样破坏形态

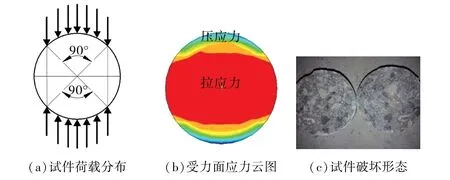
图4 混凝土圆柱体径向劈拉法的应力分布与试样破坏形态

3.2 试验数据有效性比较

标准差表示数据的离散程度，标准差越小说明数据分布越集中。 因此，试验数据的相对精度可以通过比较圆柱体径向劈拉破坏荷载与立方体劈拉破坏荷载的标准差来解释。 圆柱体径向劈拉破坏荷载标准差一般小于立方体劈拉破坏荷载标准差，说明圆柱体径向劈拉试验得到的混凝土抗拉强度值的精度不低于立方体劈拉试验（见表6）。

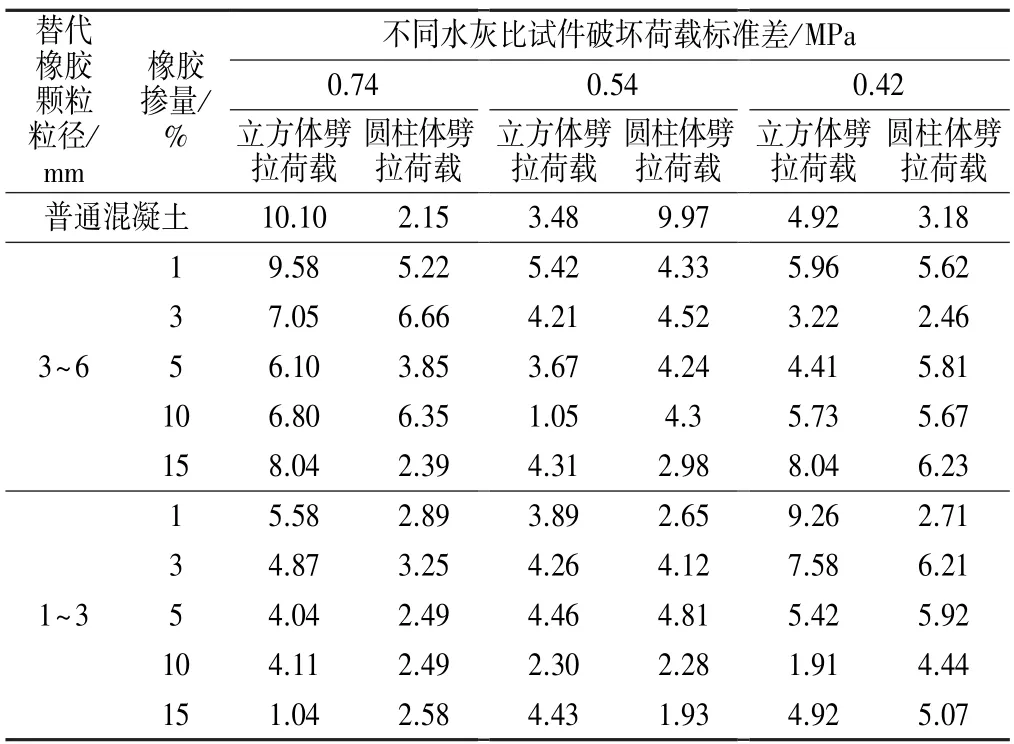
表6 立方体劈拉破坏荷载与圆柱体径向劈拉破坏荷载的标准差

3.3 普通混凝土与橡胶混凝土的劈拉强度

普通混凝土的立方体劈拉强度和圆柱体名义径向劈拉强度与水灰比呈负相关性（见图5）。 在相同水灰比条件下，圆柱体名义径向劈拉强度高于立方体劈拉强度，与他人的研究结果较为一致［17］，这主要是试样尺寸效应导致的。

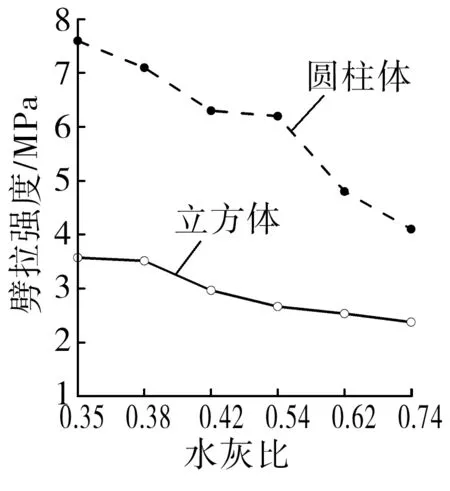
图5 普通混凝土劈拉强度与水灰比的关系

与普通混凝土相似，橡胶混凝土的立方体劈拉强度和圆柱体名义径向劈拉强度均随水灰比的增大而减小（见图6），且无论橡胶颗粒粒径大小或橡胶颗粒掺量如何，均呈相同的趋势，说明这种规律与橡胶颗粒大小和含量无关。

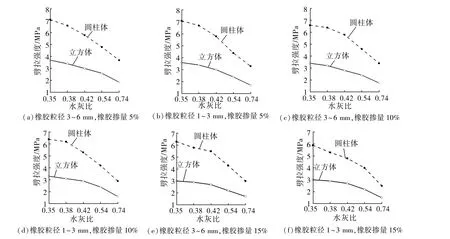
图6 橡胶混凝土劈拉强度与水灰比的关系

无论橡胶颗粒大小和水灰比水平如何，立方体劈拉强度和圆柱体名义径向劈拉强度均随着橡胶颗粒含量的增加而降低（见图7）。 原因主要是橡胶颗粒强度远低于砂体强度，橡胶与水泥之间的黏结强度远低于砂体与水泥之间的黏结强度。 橡胶颗粒含量对混凝土强度的影响与前人的试验结果相似［18-20］。

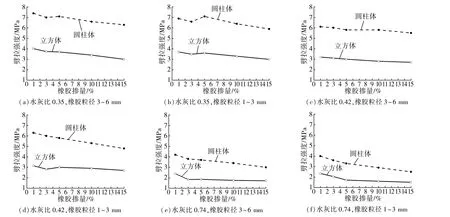
图7 橡胶混凝土劈拉强度与橡胶颗粒掺量的关系

通过以上分析可知，可以用圆柱体名义径向劈拉强度来表示混凝土的抗拉强度，在某种意义上等同于立方体劈拉强度。

3.4 立方体劈拉强度与圆柱体名义径向劈拉强度的关系

立方体劈拉强度由式（1）得出，混凝土在立方体劈拉和圆柱体径向劈拉条件下，其劈裂面的应力分布具有相似性（见图3（b）、图4（b））。 假设圆柱体径向劈拉强度与立方体劈拉强度具有相同的计算公式：（见图8（c））的差异可以看出，橡胶颗粒大小对ψ值的影响也较小。 当所有数据组合在一起时，ψ＝0.52时复相关系数R2为0.91（见图8（d））。

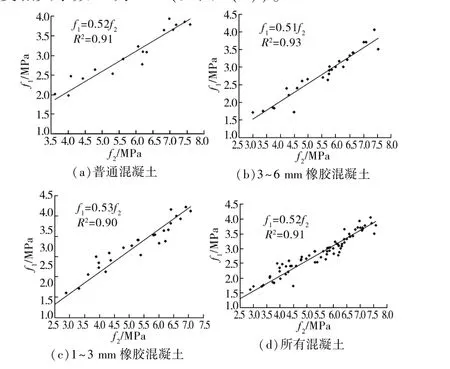
图8 式（6）的线性回归

式（6）的线性回归结果（通过原点）如图8 所示。普通混凝土的ψ值为0.52（见图8（a）），与橡胶混凝土的ψ值（0.51、0.53 见图8（b）、8（c））相差较小，说明在普通混凝土中掺入橡胶颗粒对ψ值的影响很小。从掺加3 ～6 mm 橡胶颗粒的橡胶混凝土ψ值为0.51（见图8（b））和掺加1～3 mm 橡胶混凝土ψ值为0.53

将ψ＝0.52 代入式（6）得到：

由式（7）计算得到f1值和立方体劈拉强度试验值f′1列于表7 中，共71 个数据，有17 个普通混凝土数据和54 个橡胶混凝土数据。 在71 个数据中，计算值f1与试验值f′1的比值最小值为0.80、最大值为1.34、均值为0.980、均方误差为0.080。 各比值相对集中在1.00左右（见图9）。 通过式（7）由圆柱体名义径向劈拉强度计算得到的立方体劈拉强度与立方体劈拉试验得到的结果接近。

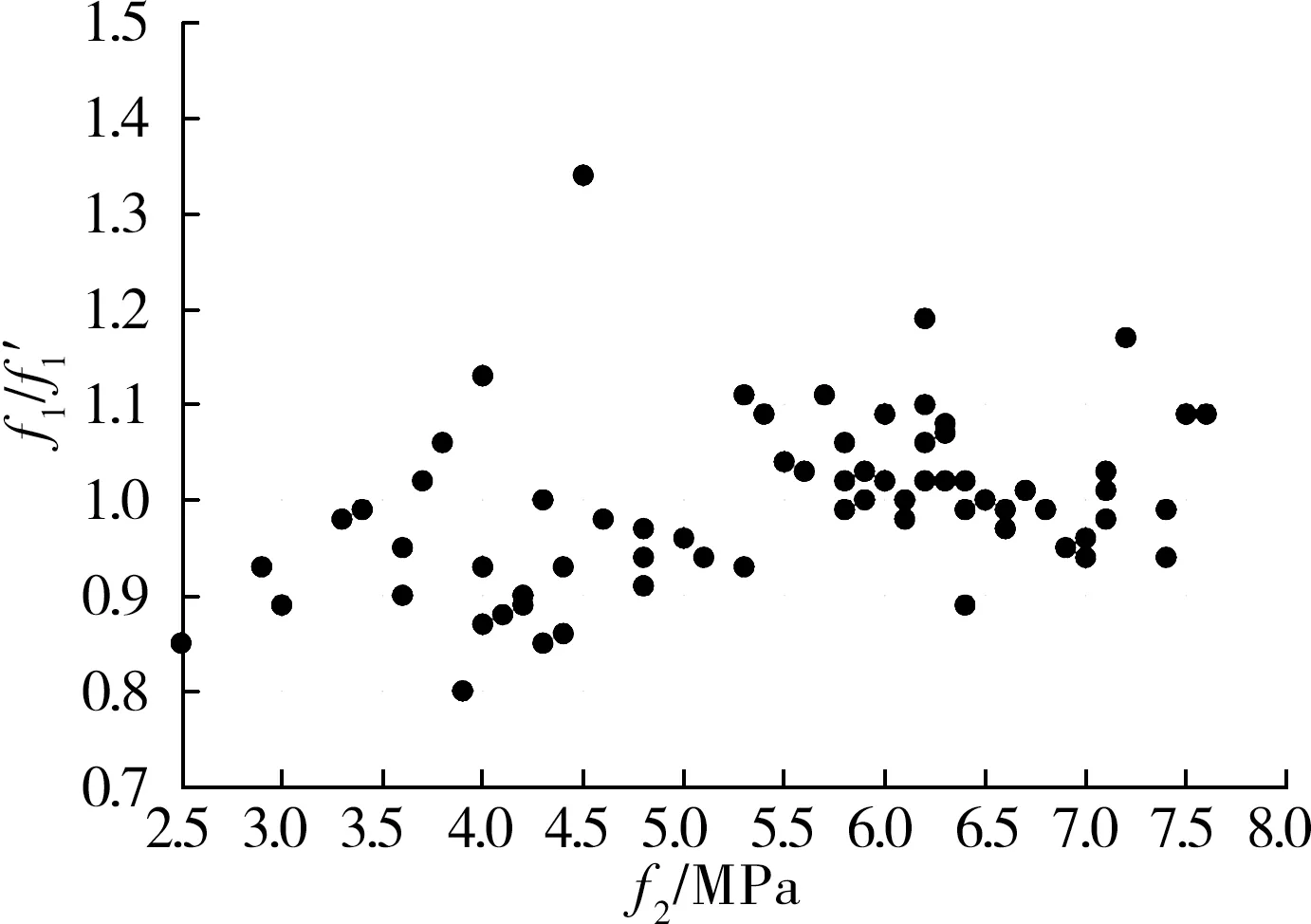
图9 立方体劈拉强度计算值与试验值的比值分布

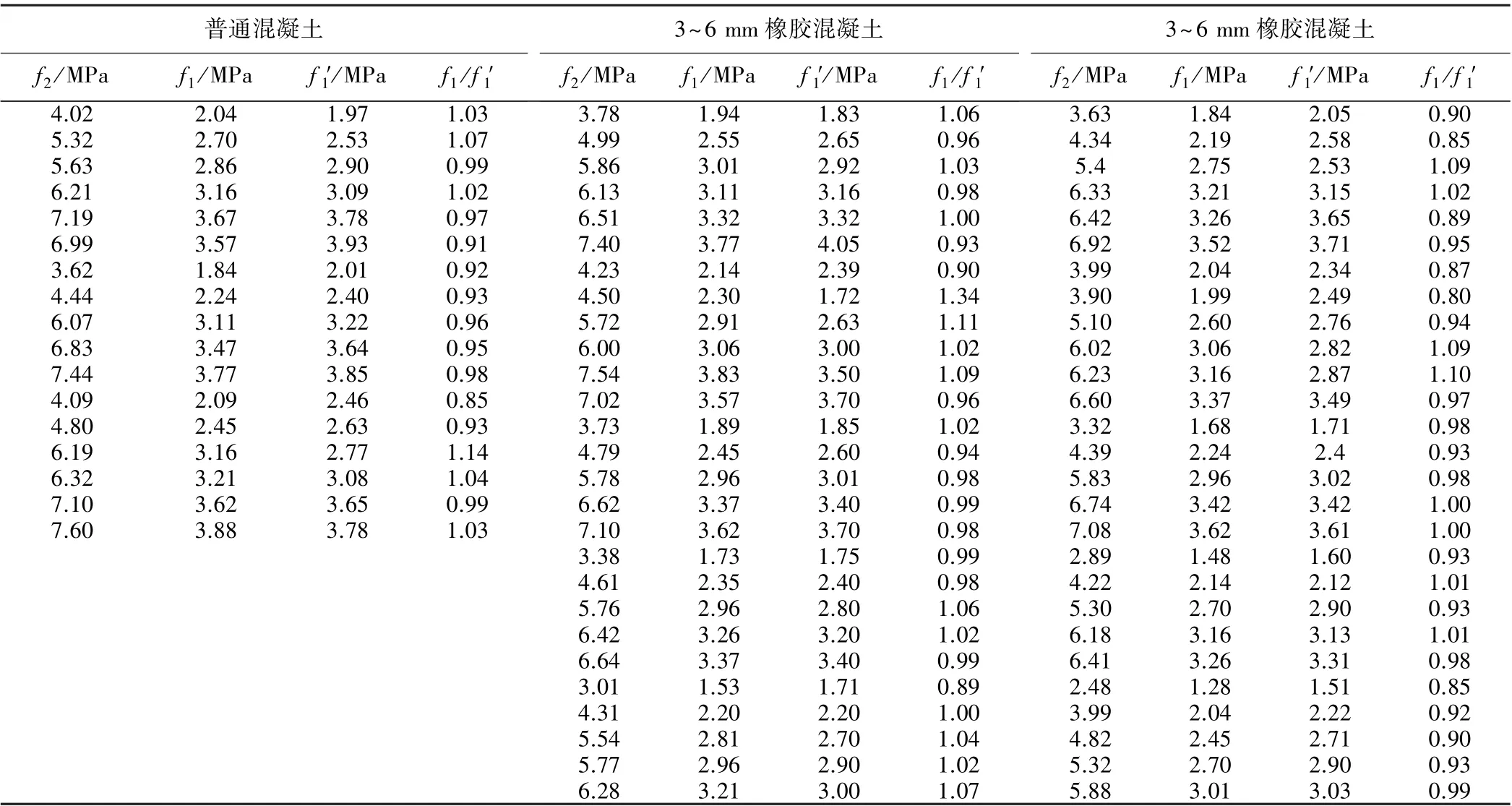
表7 混凝土劈拉强度的计算值和试验值

4 结 论

通过对普通混凝土和橡胶混凝土的立方体劈拉强度和圆柱体名义径向劈拉强度进行测定和比较，得出以下结论：

（1）利用有限元分析软件对圆柱体径向劈拉试验进行模拟，得到了混凝土受拉方向的应力分布，结果表明劈裂拉伸破坏面的拉应力分布区域较大，与立方体劈裂拉伸破坏面的应力分布相似。

（2）各组混凝土圆柱体径向劈拉破坏荷载试验的标准差略低于立方体劈拉破坏荷载试验的标准差。 这说明用圆柱体径向劈拉试验测定的混凝土抗拉强度的精度较高。

（3）普通混凝土和橡胶混凝土的立方体劈拉强度和圆柱体名义径向劈拉强度随水灰比和橡胶掺量的增加而有规律地降低，且规律相近，表明立方体劈拉强度和圆柱体名义径向劈拉强度之间存在一定的正向线性相关，可表示为f1＝0.52f2。