求解柔性作业车间调度问题的新型改进Jaya算法

裴小兵，祁文博，戴毓彤

天津理工大学 管理学院，天津 300384

在现代制造系统中，调度管理问题一直被人们认为是能够直接影响企业生产经济效益的一个关键问题，生产调度主要指通过有效合理利用现有资源来不断提高企业生产效率。柔性作业车间调度问题（flexible job shop scheduling problem，FJSP）扩展了调度问题搜索空间，增加了车间调度操作的灵活性，相较于其他传统作业生产车间，在调度管理问题方面更贴近于实际生产状况，是近年来制造生产车间调度管理领域的重要研究发展热点。为解决FJSP，许多学者采用了不同类型的智能优化算法。顾幸生等[1]在自创的问题编解码方案上建立博弈集，结合粒子群算法提出一种改进博弈粒子群算法。王家海等[2]设计了一种有效的邻域结构并讲其与进化算法结合。Li等[3]以使更优化最大求解完工后时间为目标，提出一种可以结合禁忌搜索算法的遗传算法来求解FJSP，并由此得到了几个对于基准问题相对新的最优解。Hao 等[4]提出一种可变长度的染色体编码方式，针对非支配排序遗传算法提出了自适应分层策略，仿真实验表明该改进算法可以提高生产效率。姜天华[5]首次提出了混合灰狼优化算法，将遗传算子和变邻域搜索策略相结合。田旻等[6]针对遗传算法求解FJSP的不足，设计了一种分层混合遗传算法，将种群划分为两层并结合邻域搜索进行调节。Nouri 等[7]提出了一个集成基于邻域的遗传算法和局部搜索技术的整体多智能体模型，以提高解的质量。Shen等[8]开发了一种改进的禁忌搜索算法，以解决具有序列相关设置时间的FJSP，同时考虑了最小化完工时间的性能度量。实验分析结果表明，与其他实验算法相比，该实验方法仍然具有显著的性能优越性。

从以上研究中可以看出，元启发式方法已经越来越多地被用于解决FJSP 问题，由于FJSP 的复杂性和多约束性，利用算法优化求解的时间过长成为实时调度策略的主要障碍。在不同的方法中，元启发式算法具有计算时间合理、求解质量高等优点。Rao[9]于2016 提出了一种新的元启发式算法Jaya，并将其应用于诸多领域的优化问题中。在文献[9]中，Jaya 与几种存在的mete 启发式优化算法分别进行了实验比较，实验和讨论结果验证了其中Jaya 算法的有效性。与现有的大多数元启发式算法相比，Jaya算法的优势和竞争力在于不需要调整任何特定的参数，只需要种群规模和迭代次数等常用控制参数以达到最优。并且在相对较少的函数求值次数下提供了最优结果。Jaya 算法的局限性在于无法有效地探索解空间中的区域，容易陷入局部最优解。Gao等[10]以快速最小化柔性机器工作时间负载长度为目标，采用Jaya算法快速求解柔性作业车间调度问题，与国内现有的新型启发式算法结果进行了比较，实验结果证明了该新型算法的技术优越性。Rylan等[11]在Jaya算法的基础上又引入有效的局部搜索技术，提出了一种算法I-Jaya，以最大完工时间为主要性能指标，比较了这种I-Jaya算法与其他常用元启发式算法的不同性能，验证了该类算法的性能有效性。然而，通过查阅文献可知，由于Jaya算法提出时间较晚，国内运用Jaya求解柔性作业车间调度问题的研究还较少，且运用Jaya求解调度问题仍有很大的改进空间。

综上所述，本文针对Jaya算法易陷入局部最优的缺点，提出一种结合变邻域搜索的新型改进Jaya 算法（new improved Jaya algorithm，NIJA），它有望在解决FJSP方面取得良好的性能。该算法首先用一种混沌序列与均匀分布相结合的混合策略产生初始种群，以达到保证初始种群多样性并提高初始种群质量的目的。然后结合Jaya 算法的原理提出一种更新机制实现种群进化，然后执行交叉操作持续改善种群。针对Jaya算法的缺点，结合变邻域搜索算法中有效的局部搜索机制，设计新的邻域结构强化搜索的过程，扩大搜索范围，避免算法陷入局部最优。此外，提出一种接受准则引导搜索空间的新区域，从而提高解的质量。最后经由算例与数值实验证明了所提方法的可行性和有效性。

1 柔性作业车间调度问题描述

FJSP 可以由n个工件(J1,J2,…,Jn)在m台机器(M1,M2,…,Mm)上加工，每道工序可以在一台或者多台机器上进行加工，这些工序将按预先确定的顺序在加工机器上加工，作业加工时间包括运输时间时间时间和机器设置时间[12]。对于FJSP，包含以下两个相关子问题，即确定各个工件的加工加工加工机器和确定各个机器上的加工顺序，以最小化最大完工时间为目标，其问题约束如下：

（1）同一时刻，每台机器只能加工一个工件，每个工件只能在一台机器上加工。

（2）各个工件在各台机器上的加工时间已知。

（3）各道工序一旦开始加工，中途就不能停止。

（4）每个工件只能在每台机器上进行一次加工。

（5）各工件在零时刻都可以被加工。

根据FJSP的问题假设，其模型相关符号如下所示。

公式（2）保证它们之间的优先关系，即上一个工序完成后才可进行下一道工序；公式（3）确保任一道工序的完工时间减开始时间等于其加工时间，即工序一旦开始就不能中断；公式（4）约束每台机器每次只能加工一道工序；公式（5）限定了每个工件的完工时间不可能大于总完工时间；公式（6）确定最大完工时间。

2 Jaya算法

Jaya是Rao[9]于2016年提出的一种新型元启发式算法。它的工作原理是持续改进，即解决方案趋向于朝着最优解的方向移动而远离最差解。Jaya 算法是一种单阶段算法，每次迭代只需对一个方程进行求值即可得到新解的值[13]。它还有一个优点，就是它是一种无参数算法，只需要种群规模和迭代次数两个控制参数。因此，优化参数用来获得最优解时所需的额外计算工作量被消除。与其他元启发式算法相比，Jaya算法易于理解和实现。Jaya算法的基本步骤简述如下：

步骤1 初始化种群大小，设计变量数量和终止标准。

步骤2 识别种群中最优解与最差解。

步骤3 按公式（7）在最优解和最差解的基础上得到更新解。

步骤4 将更新解与之前的解进行比较，若更新解更好则将其替换，否则保留旧方案。

步骤5 判断是否满足终止标准，若满足则报告最优解，否则返回步骤2。

3 新型改进Jaya算法

Jaya 算法的局限性在于无法有效地探索解空间中的区域，容易陷入局部最优解[14]。为了克服这一问题，本文提出一种新型改进Jaya算法。首先，该算法使用混合策略产生具有优势的初始种群，并设计了一种新的种群更新机制，对机器分配和工序排序进行了进化，向着最优解移动。然后基于相似度进行交叉操作，并运用变邻域搜索以增强挖掘邻近解的能力和保持多样性的能力，从而获得更好的解。最后提出了一种接受准则，来改善种群多样性，从而防止早期收敛。

3.1 整体算法流程框架

算法流程框架如图1所示，其基本步骤描述如下：

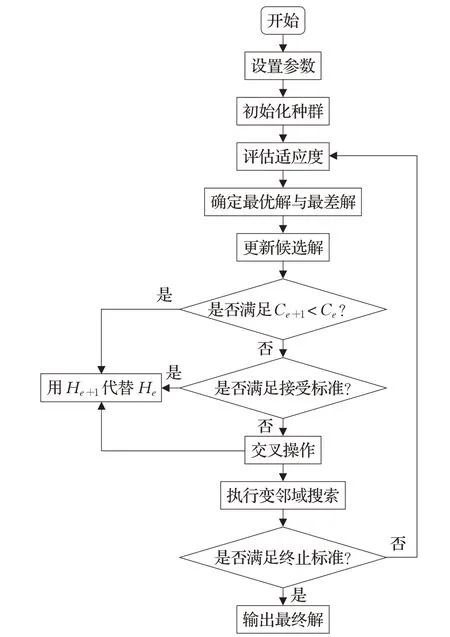
图1 算法流程框架Fig.1 Algorithm flow diagram

步骤1 设置参数，如种群大小、终止条件、工件数、机器数、工序数及相关处理时间。

步骤2 应用组合策略初始化种群。

步骤3 评估适应度，并得出所有候选解He并计算其目标函数值Ce；确定最高函数值Ce,lbest和最低函数值Ce,lworst，并将对应的两个候选解标记为Hbest和Hworst。

步骤4 使用Jaya 算法的更新机制得到新的候选解He+1并计算目标值Ce+1。

步骤5 判断是否满足Ce+1＜Ce，若满足则用He+1代替He，否则转步骤6。

步骤6 检查是否满足接受标准，若满足则用H代替He，否则保留当前解。

步骤7 计算相似度，执行交叉操作。

步骤8 将变邻域搜索机制应用于每个候选解以进一步筛选。

步骤9 判断是否满足终止标准，若满足则转到步骤11，否则转步骤10。

步骤10 返回步骤3直至满足终止标准。

步骤11 输出最优解。

3.2 编码

一个可行解应包含定义问题所涉及的所有方面，本文使用一种双层编码策略，以3个工件，9个工序，4个机器的问题为例，如图2所示。每个数组的结构长度转换为工序总数，该例中工序顺序为（O21，O31，O11，O32，O12，O22，O13，O33，O23）。工序顺序上的数组表示工件索引，机器分配数组表示分配机器的索引，所述索引来自可选机器集，相同索引表示同一工件的前后工序。

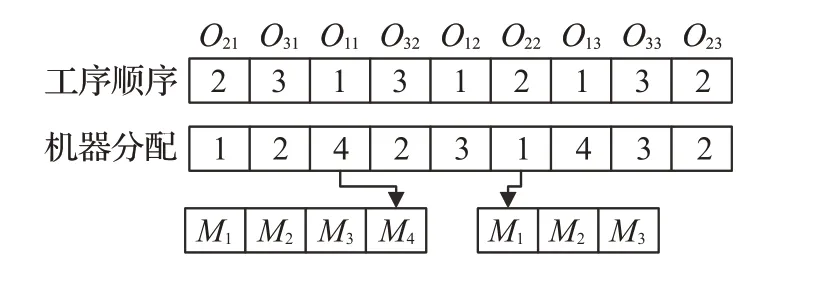
图2 编码示意图Fig.2 Coding schematic

3.3 初始化种群

初始种群的质量对算法产生最优解的过程有着很大的影响[15]，本文采用一种随机分布与混沌序列相结合的混合策略产生初试种群，使候选解随着迭代次数的增多而趋于全局均匀分布。该操作主要分为两个阶段，工序排序阶段和机器分配阶段，每一道工序的机器都采用混沌序列的方法从可选机器集中产生，根据混沌序列公式生成伪随机序列。在此过程中实时统计所有机器的被使用次数并计算使用次数均值，当某台机器的使用次数达到平均值，则优先使用其他机器处理该工序，这样可保证机器负荷平衡。不断重复上述步骤，直至生成完整初始种群。具体步骤描述如下：

步骤2 对每个工序随机产生一个rand值，其中rand∈[0,1] ，根据rand值的大小对所有工序进行升序排序，如图3所示。

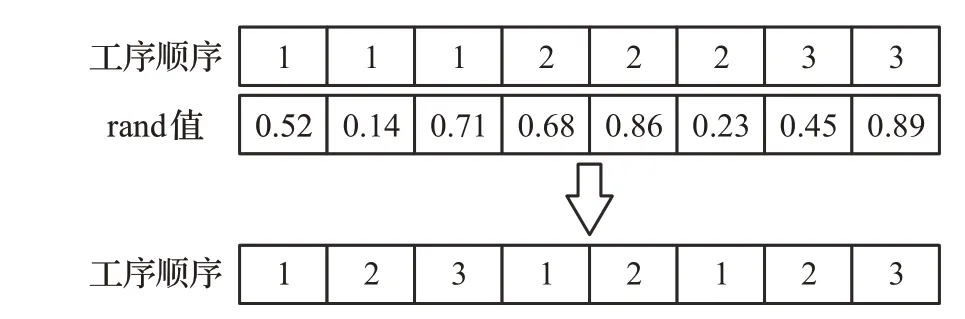
图3 工序排序Fig.3 Operation sequencing

步骤3 对机器分配随机产生一组数值，通过公式pn+1=μpn(1 -pn)，其中μ∈( 0,4],pn∈( 0,1) ，生成具有混沌特性的随机序列，依据一一映射在可选机器集中，确定机器编码。

步骤4 统计所有机器的被使用次数，若某机器已达到平均被使用次数，则该工序优先使用其他机器。

3.4 个体位置更新机制

Jaya算法基于一个原则：目标函数的解朝着最优解移动而远离最差解[16]。根据这些概念提出一种适用于FJSP 的更新机制，既通过从一组可选机器中分配适当机器，之后再确定工序顺序进行求解[17]。通过消除与最差个体对应的编码并在保持可行性的同时合并最佳个体编码来修改个体，生成更新解，实现种群进化[18]。

3.4.1 机器分配更新机制

首先计算当前种群中所有可行解的目标函数值，找出最优值Ce,lbest与最差值Ce,lworst，并找出对应的候选解决方案Hbest和Hworst，执行更新机制，如图4所示，图中数组为相应分配机器的索引，首先确定候选解He与最差解Hworst之间相同的机器并从中删除，然后将Hbest相应位置的机器放入He中，生成新的候选解He+1。以此类推，更新所有候选解。确定机器分配的Jaya更新机制主要步骤如下：

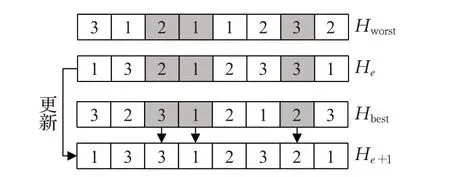
图4 机器分配更新机制Fig.4 Updating mechanism for machine assignment

步骤1 在Hbest和Hworst之间确定相同编码的加工机器并从He中删除。

步骤2 将He中剩余的机器复制到He+1相应位置中。

步骤3 复制Hbest的相应位置的机器放到He+1的空白位置中。

步骤4 根据相应可行机器集检查更新解He+1的可行性，若不可行，则在可选机器集范围内随机分配一个机器。

3.4.2 工序排序更新机制

与机器分配更新机制原理相似，提出了工序排序的Jaya更新机制，找出最优值Ce,lbest与最差值Ce,lworst以及对应的解决方案Hbest与Hworst，图5中数组为相应工件索引，确定候选解He与最差解Hworst之间相同位置的工件并从中剔除，然后将He剩余工件复制到He+1中的相应位置。剔除Hbest中He的剩余工件，最后将Hbest的剩余工件添加到He+1的空白位置中，生成新的工序顺序从而生成候选解He+1。保证了调度的可行性，从而消除了调度修复过程，减少了计算量，其主要步骤如下：

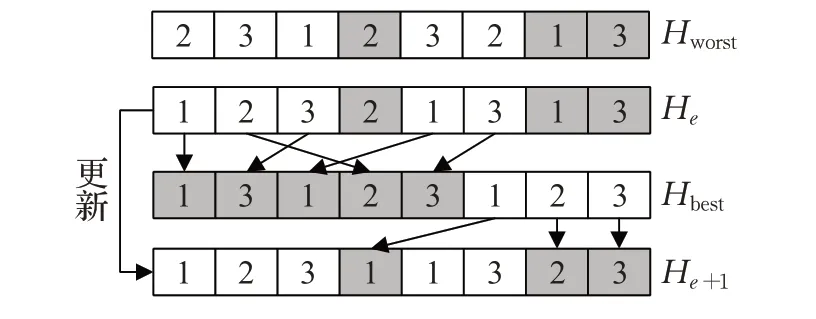
图5 工序排序更新机制Fig.5 Updating mechanism for operation sequencing

步骤1 在He和Hworst之间确定相同的分配工件并从He中删除。

步骤2 将He中剩余的工件复制到He+1中。

步骤3 从Hbest中删除He+1中的剩余工件。

步骤4 复制Hbest的相应工件放到He+1的空白位置中。

3.5 交叉操作

交叉算子本质上是通过搜索解空间中的新区域来改善候选解，一个好的交叉算子应该能够有效地在后续种群之间交换信息[19]。目前文献中广泛使用的是基于优先保持顺序的POX 交叉。但通过实验可以观察到，在搜索过程后期，工序序列向量中具有相似位置的元素，这使得交叉操作趋于无效化。为克服这一缺点，本文提出一种基于相似度的SPOX 交叉。为有助于交叉操作几件维护与父代之间的联系，基于相似性的递减值将工件分配给子代，这也有助于提高搜索过程的收敛性。每个工件相似度由公式（8）计算得到：

其中Ii表示两个工序顺序编码中具有相同工件分配的位置总数，Ji表示工件i的总工序数。如图6 所示，图中数组为相应工件的索引，工序顺序交叉操作过程如下：

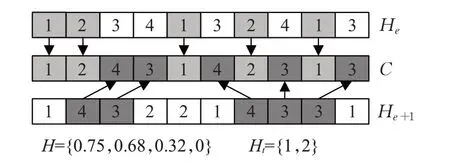
图6 工序排序交叉操作Fig.6 Operation of operation cross

步骤1 根据公式（8）计算He+1与He各工件的Xi值。

步骤2 若所有Xi都等于各工件工序数，则执行步骤3，若Xi值都等于0 则执行步骤4、6，否则执行步骤5、6。

步骤3 随机选择一个工序Oi，插入子代的第一个基因位，将受影响的工序向后移动，指导Oi的位置。

步骤4 随机分配一半的工件给子集Ht。

步骤5 根据Xi的递减值将一半的工件分配给子集Ht。

步骤6 将属于子集Ht的工件从He+1中插入子代相同位置，将子集Ht的其余工件从He中从左到右依次插入子代。

如图7 所示，图中数组为相应分配机器的索引，机器分配的交叉操作通过当前He+1与旧种群He生成新的子代，过程如下：

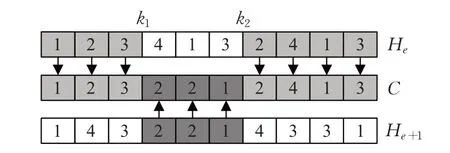
图7 机器分配交叉操作Fig.7 Machine assignment cross operation

步骤1 选择两个随机数k1和k2，使1 ≤k1＜k2＜Ji，k1和k2分别表示要交换的元素集合开始与结束的位置。

步骤2 将He中k1到k2位置上的元素复制到子代中相应位置，He+1中所有其他元素追加到相应位置。

步骤3 检查可行性，若不可行，则在可选机器集范围内随机分配一个机器。

3.6 变邻域搜索算法

变邻域搜索算法是一种有效的局部搜索算法，它在搜索过程中的基本思想为，在当前解的不同邻域之间切换来扩展搜索范围以进行局部寻优，避免陷入局部最优解[20]。

为进一步提高算法的搜索能力，每次迭代都采用变邻域搜索机制，从而达到减少计算量的同时生成质量更高的解。变邻域搜索的本质在于通过邻域的系统变化来搜索解空间。事实上，随机选择编码进行逆序操作功能允许两个领域结构中的每一个隔离自己的探索区域，而协作机制启动多个搜索，随机变化最佳解决方案信息，从而加速探索过程[21]。因此，设计几个覆盖整个解决方案空间的邻域结构是必要的[22]。考虑到解决方案表示和特定问题的特征，本文在运用传统的交换、插入邻域结构的基础上，又设计了两种邻域结构N2、N3，以实现邻域搜索。

（1）邻域结构N1：插入，在任意一个OS编码段上随机选择两个位置，将靠后位置的工件插入到靠前位置的工件前，前一位置之后的工件按顺序向后顺延，如图8中（a）所示。

（2）邻域结构N2：在任意一个OS 编码段上随机选择x个位置，其中1 ＜x≤3 ，且x个位置上的编码不完全相同，将x个编码位置上的编码顺序进行逆序操作，生成邻域解，如图8（b）所示。

（3）邻域结构N3：随机在任意一个OS 编码段内选择一个编码位置，判断该位置编码与前一相邻位置的编码是否相同，若相同，则将其与后邻编码交换，若不同则继续判断该位置的编码与后一相邻位置的编码是否相同，若相同，则将其与前邻编码交换；若不同，则将其与前后相邻位置的编码进行随机变化。变换机制如图8（c）所示。

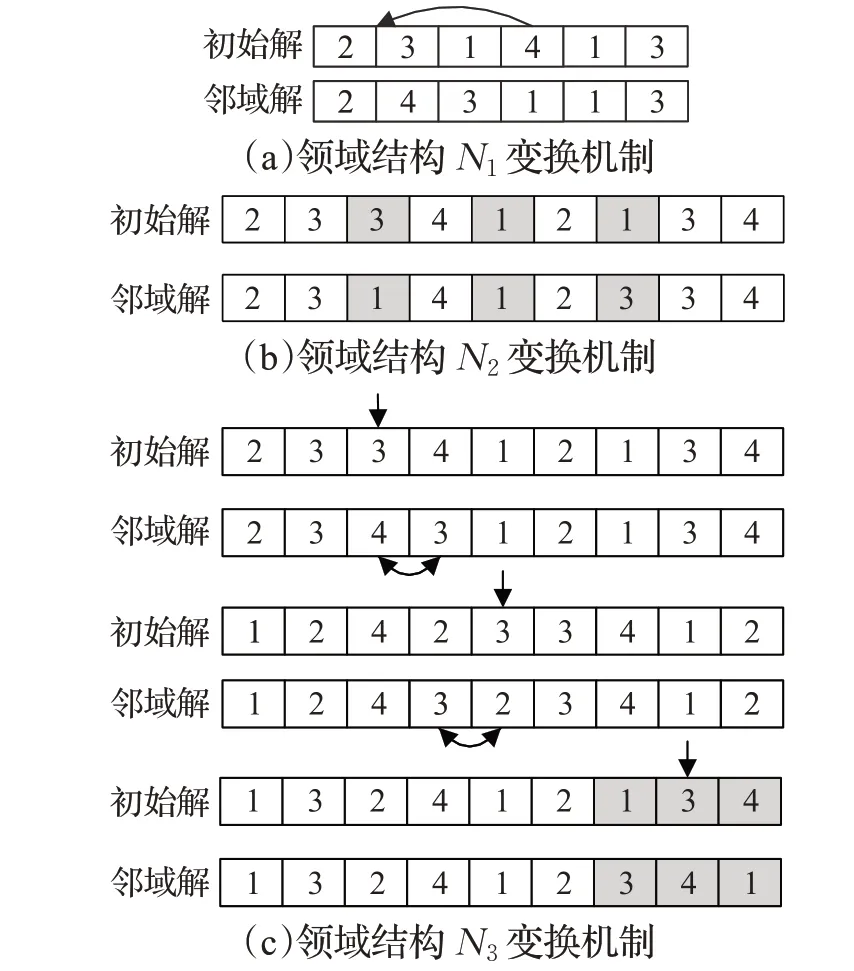
图8 邻域结构变换机制Fig.8 Transformation mechanism of neighborhood structure

3.7 接收准则

针对最大完成时间值大于当前解的生成解，给出了一个可接受准则，该接收准则与模拟退火中的准则相似，但在方程中消除了温度参数，从而消除了调整参数的过程。这一操作通过在解空间中探索新的区域搜索有希望的解，以帮助改善种群多样性，防止早期收敛[23]。建议的接受准则为：

其中Cmax是当前解的最大完工时间值，C′max是新解的最大完工时间值，rand表示[ ]0,1 中随机生成的数字。将最大完工时间值的相对偏差作为验收度量，偏差越小，接受具有更高最大完工时间值的新解的概率越高。

4 仿真实验

本研究采用MATLAB 软件实现，程序在处理器为Intel Core i5 处理器，2.11 GHz 主频，16 GB 内存，操作系统为64位Windows10的计算机上运行。将提出的方法与文献中的几种算法在makespan和计算时间方面做了详细比较。考虑参数值如表1所示。

表1 参数设置Table 1 Parameter setting

4.1 变邻域搜索有效性验证

为了验证本文所提出方法的求解过程的有效性，将本文所提算法与无局部搜索的Jaya 算法，针对算例MK09进行仿真实验，算法的收敛过程如图9所示，图中实线为NIJA，虚线为Jaya。可以注意到NIJA 在第142次迭代中收敛到最佳完工时间，而Jaya在181次迭代中收敛到最佳完工时间，收敛曲线表明，在搜索空间内执行提出的变邻域搜索，由于搜索过程的加强，最大完工时间逐渐减小。

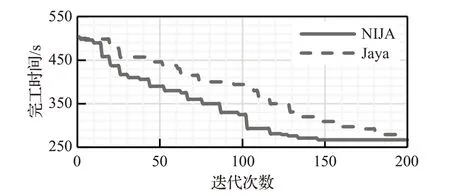
图9 MK09算例收敛图Fig.9 Convergence graph of MK09

4.2 算法有效性验证

为进一步验证本文所提出方法的求解过程的有效性，分别针对算例Kacem[24]和算例Brandimarte[25]进行验证，运用新型混合Jaya算法独立运行30次，并将取得的最优值Cmax与其他文献中算法的最优值进行对比。

首先对Kacem的8×8、10×10、15×15的3个算例进行验证比较，包括改进Jaya算法（IJA）[11]、改进变邻域算法（IVNS）[26]、MBBO[27]、IACO[28]。通过表2可知，该算法所求得的Cmax值与其他算法最优解都没有偏差，证明了该方法的有效性和稳定性，且在求解时间上，该算法明显优于其他算法。算法求解结果的各甘特图分别如图10～12。

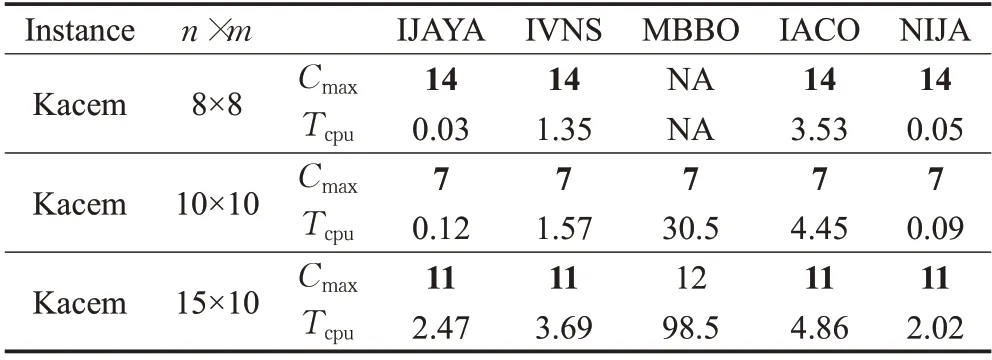
表2 Kacem算例对比结果Table 2 Comparison results of Kacem example

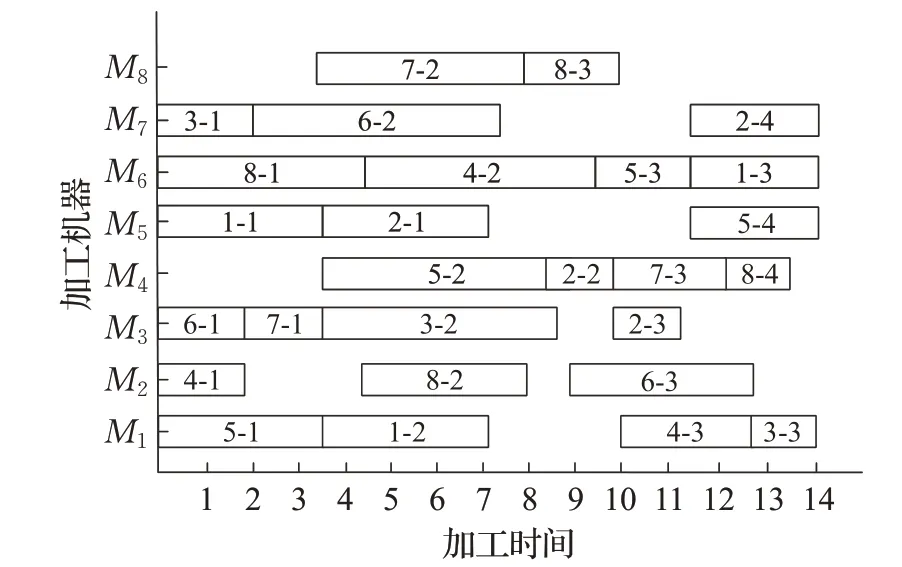
图10 8×8甘特图Fig.10 8×8 Gantt chart

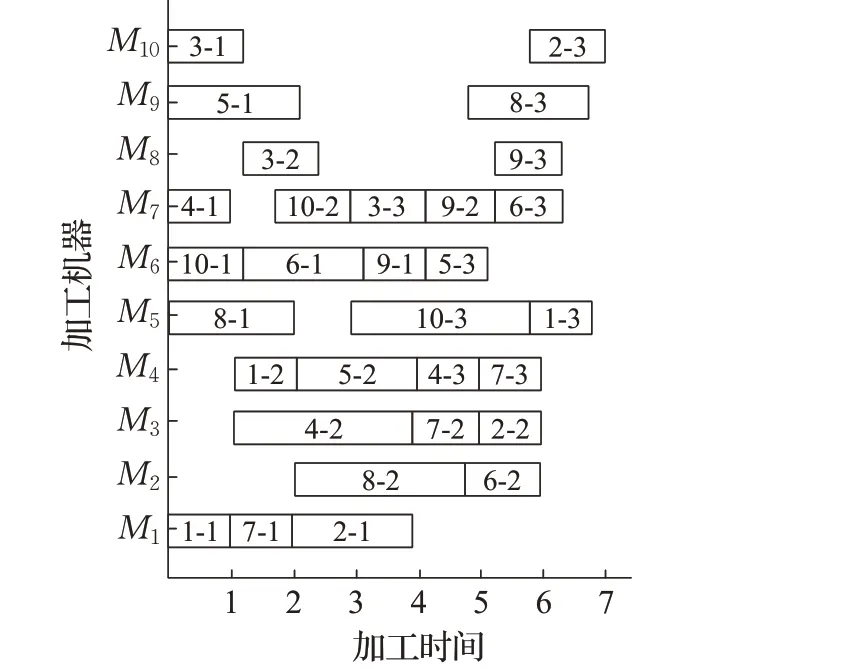
图11 8×10甘特图Fig.11 8×8 Gantt chart

图12 10×10甘特图Fig.12 10×10 Gantt chart

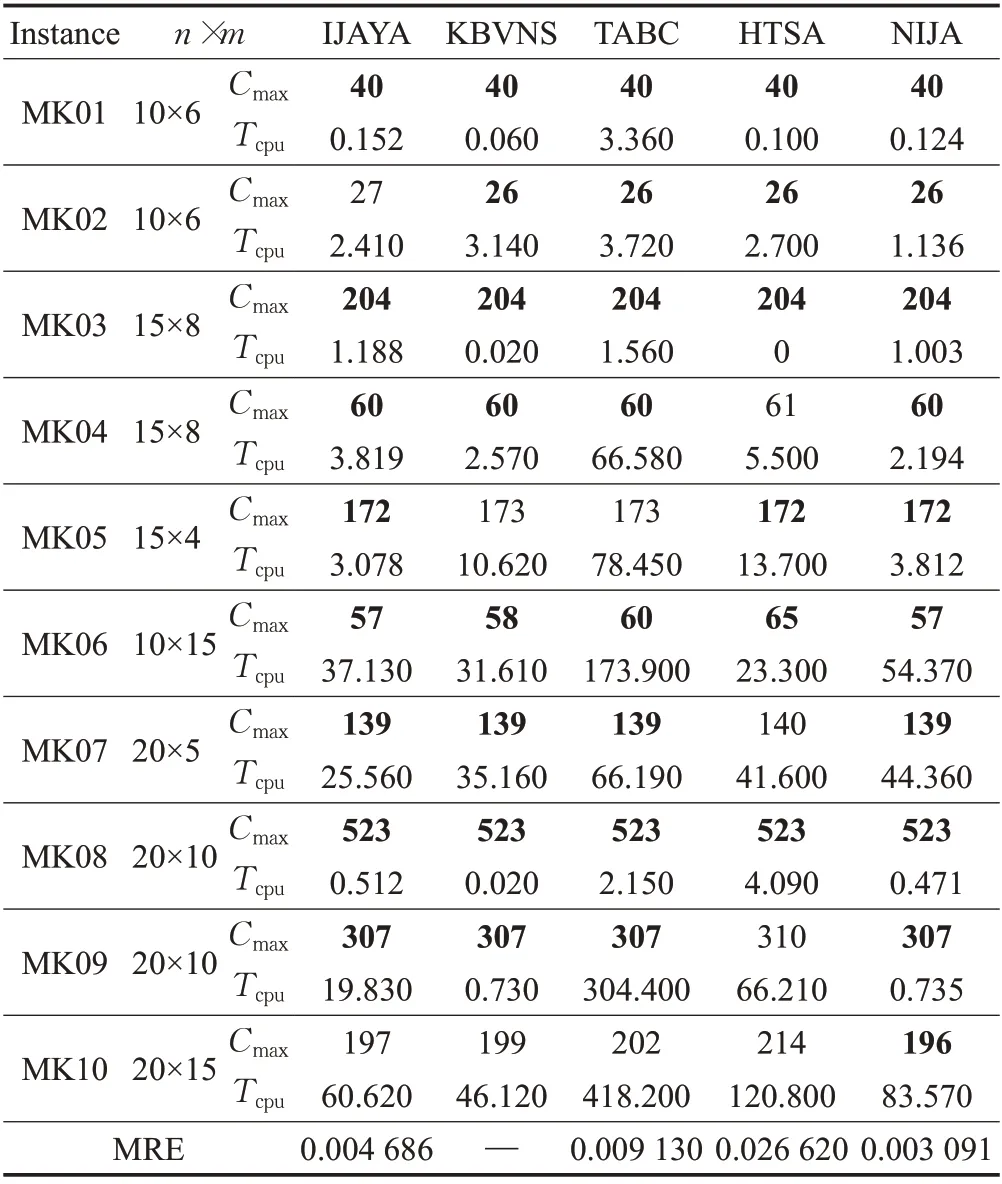
表3 Brandimarte算例对比结果Table 3 Comparison results of Brandimarte example

5 结束语

Jaya算法是一种无参数算法，其优点是算法结构简单，可应用性强，能够在较少的求解次数下提供最优结果，但容易过早收敛并陷入局部最优。由于求解FJSP的复杂性，用单一的搜索算子很难有效地解决问题。该算法将初始化与基于Jaya 的更新机制、交叉算子、变邻域搜索融合在一起，强调在寻优过程中种群的多样性。为此，本文提出了一种新型改进Jaya算法。（1）对初始解的产生方式进行了改进，以保证初始种群的多样性。（2）利用Jaya 算法的原理提出新的更新机制，找出优势基因，进化种群，降低求解复杂性。（3）提出一种基于相似度的交叉操作，改善种群多样性防止早期收敛。（4）结合变邻域搜索算法设计了一种局部搜索机制，克服了Jaya算法的缺点，使搜索过程的广度与深度得到平衡。

本文针对算例进行仿真并验证了该算法在解决FJSP上能够获得较稳定的解，同时提高了求解效率。由于Jaya算法提出时间较晚，国内运用Jaya求解柔性作业车间调度问题的研究还较少，且运用Jaya求解大规模调度问题仍有很大的改进空间。未来研究中，将考虑与其他智能优化算法相结合，并应用其他类型的组合优化问题。