基于注意力机制的点云神经网络架构搜索方法

谭台哲，黄永耀，杨 卓，刘 洋

广东工业大学 计算机学院，广州 510006

深度学习已经在图像相关的领域取得了很好的效果。其中的卷积神经网络（CNN）在图像分类任务[1]、语义分割任务[2]、目标检测任务[3]中都达到了行业领先的成果。由于三维点云处理在自动驾驶、机器人空间理解领域具有重要意义[4]，最近有许多研究致力于将神经网络应用到三维点云数据处理中，但原始的三维点云是非规则数据，每个点只包括了三维坐标(x,y,z)和RGB信息，无法用处理图像的规则卷积核进行特征提取。早期的方法通常是先将原始三维点云预处理成网格状数据，然后直接采用规则的三维卷积核进行特征提取，这种方法通常具有较高的计算复杂度。PointNet[5]的提出为基于神经网络的三维点云处理带来了一种全新的思路，它不需要额外的预处理，且通过叠加多层感知机（MLP）的方法直接对原始三维点云进行特征提取，大幅减少了计算消耗，在当时达到了比较领先的精度。从此之后，有许多面向三维点云的神经网络方法被提出，这些方法主要可以分为三种：基于图的方法[6-7]、结构化表示方法[8-9]、基于点卷积的方法[5，10-12]。

然而，在不同类型的数据集中（如经过激光雷达采集、D-RGB 摄像头采集的点云数据集），点云分布情况并不统一，所以在现实应用场景中仍需要面向不同类型的数据集进行神经网络的人工调整以达到较好的拟合度，但是这样的工作通常需要较高的人工成本，并且要求相关人员具有丰富的深度学习领域相关知识。最近得到大力发展的自动神经网络架构搜索（neural architecture search，NAS）技术，则可以最大程度地减少神经网络设计中人工介入的影响，并能高效率地优化神经网络。但是目前在计算机视觉领域中，大量的NAS 技术研究只聚集在图像数据上，面向三维点云数据的NAS技术仍处于初始阶段，本文的工作则是在这个方向上的一个探索。

NAS技术主要包括两个关键问题，即搜索空间和搜索算法。搜索空间中定义了各种用于组成搜索单元的候选操作（比如3×3 卷积、最大池化等），以及由这些候选操作结合而成的搜索单元。由多个搜索单元叠加而成的神经网络将作为搜索空间，搜索算法则是用于迭代地从搜索空间中搜索出最优的神经网络，搜索算法可以大致分为进化算法[13]、强化学习算法[14-15]。文献[14]提出的基于强化学习算法虽然表现出良好的效果，但仍然需要大量计算资源。在这之后提出的方法DARTS[16]以及其变体[17]将网络架构搜索设计为一个可微分的方式，允许搜索算法使用梯度下降进行网络架构搜索，从而大幅降低计算复杂度。2020年提出的SGAS[18]则实现了更进一步的改进，其能在少量样本的数据集中搜索出具有优秀泛化能力的神经网络。同时，SGAS 也是第一个将NAS技术应用到三维点云处理的方法，其采用了图卷积核（graph convolution）组成搜索空间，并以此搜索出图卷积神经网络（graph convolution network，GCN），这在三维点云处理方法分类中属于基于图卷积的方法。相比基于点卷积的方法，这种方法在反向传播中需要保存更多的中间变量，会占用更多的显存空间，导致这类方法难以适用于大规模点云数据中。针对这个问题以及高效的三维点云特征提取问题，本文提出了一种基于点卷积的神经网络架构搜索方法，对于搜索算法，则沿用了SGAS的工作。对于搜索空间的组成，本文提出了一种新的基于点卷积的搜索单元。

由于点云数据下采样的特殊性，不同尺度点云之间的语义信息会产生较大的差异，直接采用面向图像的搜索单元结构的方案无法获得理想的效果。为了增强不同尺度点云的信息融合，本文提出了一种基于注意力机制的多尺度融合模块，取代标准搜索单元中原有的输入节点处理模块。另外，本文采用了两个基于点卷积的特征提取器，其中包括了多层感知机形式的特征提取器（MLP点卷积核）和多层分离卷积核构成的特征提取器（shell点卷积核），并设计了特殊的面向点云的下采样模块与之相结合，用以构成候选操作并组合成一个搜索单元。本文的主要贡献如下：

（1）提出了一种基于注意力机制的多尺度融合模块，其增强了两个尺度点云的信息融合，改善了直接下采样导致不同尺度点云之间的语义信息差异过大的问题。另外，由于引入了注意力机制，增强了全局语义信息，从而提高了模型的特征提取能力。

（2）通过采用该多尺度融合模块以及设计一系列候选操作组成搜索单元，提出了一种基于点卷积的搜索空间。相比基于图卷积的搜索空间，其计算效率有较大提升。

（3）采用SGAS搜索算法在搜索空间中搜索出最优的神经网络，在ModelNet公开数据集[9]上的对比实验表明，相比于传统人工设计的神经网络，该方法可以在很短时间内自动搜索出具有很少可学习参数的神经网络，并且能获得比较领先的性能。相比基于图卷积的SGAS方法，本文提出的基于点卷积的方法搜索得到的神经网络，减少了约70%的可学习参数量，并且能维持相近的性能。消融实验也证明了采用本文提出的基于注意力机制的多尺度融合模块可以带来1.1%的精度提升。另外，本文首次提出用基于点卷积的搜索空间进行面向点云的神经网络架构搜索。

1 相关工作

1.1 面向三维点云的特征提取方法

1.1.1 结构表示方法

早期提出的三维数据处理方法是将不规则的三维点云转换成规则结构的数据，比如体素（voxel）[8]、多视图[9]、层次数据结构[19]，再用标准卷积神经网络进行特征提取。其中多视图方法将三维点云投影成多个视点的图像，对于单个目标的分类任务，这类方法有一定的效果，但对于语义分割等任务，这类方法会由于物体遮挡问题而丢失部分物体信息，导致性能不佳。层次数据结构方法通常将点云采样为层次结构数据，比如八叉树（OC-tree），再利用特殊的层次结构对这种数据进行学习，这类方法需要大量的数据预处理，通常会导致过多的计算消耗。基于体素的方法则是在预处理过程中，将三维点云等距离采样成三维网格状数据，并输入到由规则的三维卷积核构成的卷积神经网络中，这些方法通常不考虑点云数据的稀疏性，会对空间中的大量空白区域进行卷积运算，产生了大量的额外计算量。本文提出的是基于点卷积的方法，只对空间中存在的点进行卷积运算，而且不需要预处理过程，从而减少了计算量。

1.1.2 基于图的方法

通过建立三维点云中各点之间的关系，基于图的方法可以对这些图结构数据进行图卷积计算，并逐层提取高层特征。对一个图结构进行卷积，可以被定义为在其频域上的卷积，比如ChebNet[6]采用Chebyshev多项式基来模拟谱滤波器（spectral filters），从而减少图的傅里叶变换时的计算消耗。另外，文献[7]专注于研究流形曲面表征，从而避免了谱域（spectral domain）计算。虽然图卷积能够在局部曲面点集上聚集特征并维持了点云的平移不变性，但是很难合理有效地定义任意两个点之间的关系。

1.1.3 基于点卷积的方法

PointNet[5]是第一个用神经网络直接处理原始点云的方法。通过将每个点输入到一个共享权值的多层感知机（MLP），PointNet 可以维持点云的平移不变性，这是因为多层感知机具有逼近任何连续函数的能力。延续PointNet 的思想，后续的一些研究工作[10-11]专注于用多层感知机来设计对局部聚合点进行特征提取的神经网络，这些研究都获得了很好的效果。这类方法会将多个局部点集的三维坐标信息和上下文语意特征一同输入到共享权值的多层感知机中进行特征提取，实现一种类似卷积的计算，所以可以看成是一种基于点卷积的方法。为了能让神经网络更好地学习空间特征和上下文语义特征，一些最近的研究工作[12，20]则采用了空间滤波器（spatial filter）来处理点云组成的特征图。这些方法用点的三维坐标来定义一个局部空间滤波器，用这个滤波器来处理相应点的上下文语意特征。这类方法充分利用了点云的三维坐标信息，从而提高了预测精度。

1.2 网络架构搜索

人工设计的神经网络在目前已经取得了很大的成功，但人工设计神经网络的方法仍有相当大的局限性，不仅仅需要面向不同数据集重新调整神经网络，投入大量的人力成本进行迭代优化，而且这些工作都要求设计人员具有一定的深度学习研究经验。为了解决这些问题，神经网络架构搜索（neural architecture search，NAS）被提出。文献[14]最早提出用强化学习算法来自动化神经网络架构搜索过程，此后提出的NASNet[15]则是基于一个起始细胞结构的搜索空间迭代地搜索神经网络，并采用正则化和权重共享技术来提高搜索效率。最近的一些研究工作[21-22]通过训练单个具有继承或者共享权值的过度参数化（over-parameterization）网络，以此来减少计算消耗。其中比较经典的是DARTS 方法[16]，其将网络的表示松弛到连续空间中并使搜索过程变成可微分形式，允许搜索算法使用梯度下降进行网络结构搜索，从而大幅降低计算复杂度。此后提出的SGAS 方法[18]则延续了DARTS 的思想，以贪婪的方式来对候选的节点操作进行选择和剪枝，并在搜索过程中提高了训练集和测试集之间的关联度，在最终测试集中达到较好的效果。为了让提出的方法有更高的性能，本文采用了SGAS作为其中的搜索算法，但实际上本文提出的搜索空间适用于所有基于DARTS的搜索算法。

2 基于可微分的神经网络架构搜索算法

但是DARTS方法存在搜索阶段和评估阶段的最优网络有一定结构差距的问题，以及DARTS 中权值共享带来的问题，使得搜索阶段得到的最优网络无法在评估阶段中达到最优效果，这个问题被称为退化的搜索评估相关性（degenerate search-evaluation correlation）[18]。为了解决这个问题，SGAS提出在搜索阶段以贪婪的方式逐步确定和修剪每个操作o(i,j)，并加入了3个衡量指标和评估准则，使得SGAS搜索得到的神经网络能在评估数据集有更好的表现。本文方法分别采用DARTS 和SGAS 搜索算法在基于点卷积的搜索空间中进行神经网络架构搜索，并加上一个分类头（classification head）模块，最终得到一个可用于三维点云分类任务的神经网络，并在实验中对比了这两种方法在点云数据上的性能。

3 基于点卷积的搜索空间

3.1 搜索空间的构成

基于点卷积的搜索空间是由多个搜索单元（cell）叠加而成，一个简单的搜索空间如图2 所示，下采样搜索单元是在正常搜索单元的基础上增加了下采样步骤，从而输出一个尺寸缩小的特征图。对于每一个在下采样搜索单元后的正常搜索单元，都是由一个基于注意力机制的多尺度融合模块和基于点卷积的候选操作组成，下采样搜索单元则不含基于注意力机制的多尺度融合模块。

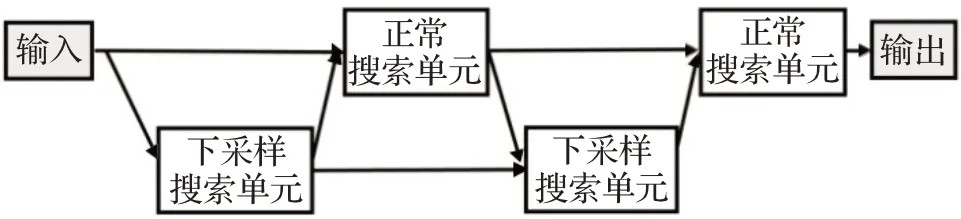
图2 一个简单的搜索空间Fig.2 A simple search space

3.2 基于注意力机制的多尺度融合模块

面向图像的搜索单元如图3 所示，具有如下结构：两个不同尺度的特征图S0 和S1 输入到搜索单元，其较大尺度的特征图S0 会直接下采样至特征图S1 的大小，从而保持两个输入特征图具有相同的分辨率，这两个经过处理后的特征图将输入到候选操作组合模块中。这个步骤在图像数据上是可行的，但根据实验观察，在点云数据中使用这种思路设计的模型效果较差。这是由于点云的下采样方式（如最远点采样、随机采样）是一种非均匀下采样，这与使用等距离采样的图像下采样方式相比更不稳定。

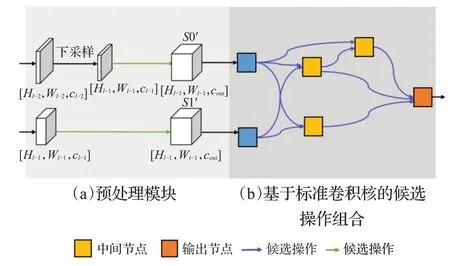
图3 面向图像的搜索单元Fig.3 Search cell for image

为了让搜索单元能更好地融合这两个不同尺度的点云数据，并使这两个不同尺度的输入数据转化成同一个尺度。受文献[23]的启发，本文提出一种基于注意力机制的多尺度融合模块。该模块具体细节如图4（a）所示，首先，较大尺度点云数据S0 作为关键点（key），较小尺度的点云数据S1作为注意力机制中的查询点（query），经过一系列的基于注意力机制的矩阵运算之后将得到一个与S1 的尺度一致的点云数据S0′，代表经过处理后的S0 的数据。给定输入的点云数据S0 和S1 的特征图分别为F0和F1，其中F0∈RNl-2×Cl-2，F1∈RNl-1×Cl-1，且Cl-2和Cl-1代表F0和F1的特征通道数。这个过程可以用如下公式表示：

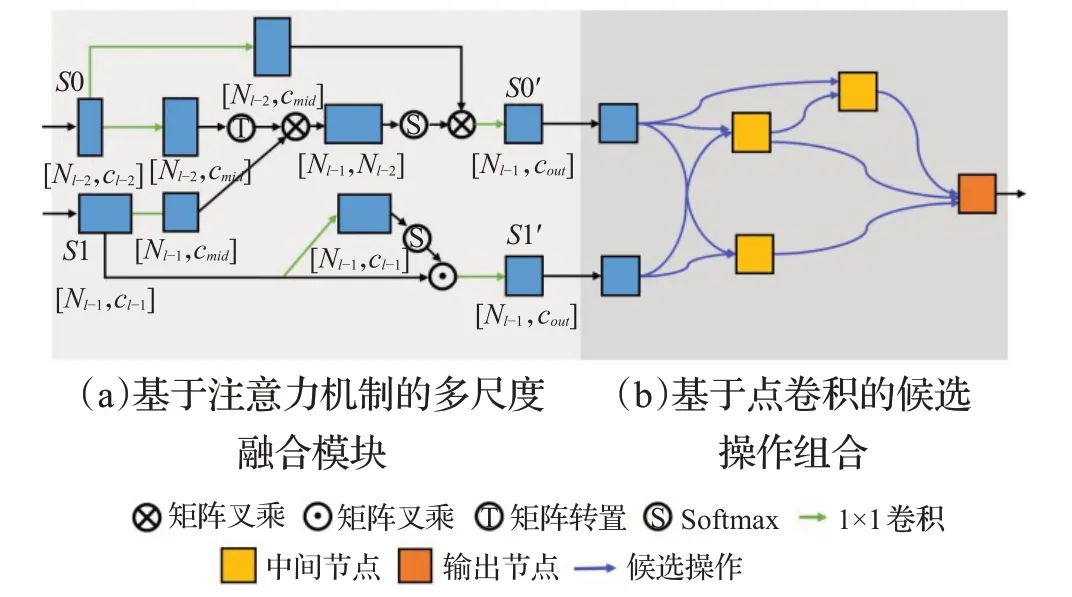
图4 具有注意力机制的搜索单元Fig.4 Search cell with attention mechanism

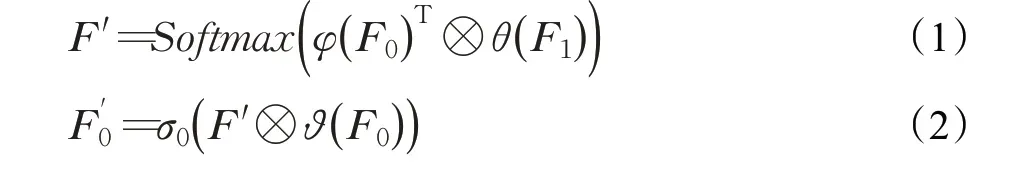
其中，⊗代表矩阵叉乘；θ、φ、ϑ、σ0都是非线性卷积层，可以采用1×1卷积代替；θ、φ、ϑ是用于生成注意力图，σ0则是用于融合全局语义信息和调整特征通道数。这个设计思想来自于自注意力结构（self-attention）[23]，在自注意力结构中，键值矩阵（key）和查询矩阵（query）由一个输入特征图经过两组1×1卷积计算得到，之后键值矩阵和查询矩阵进行点乘得到一个全局的特征图注意力权重，最后与值矩阵（value）进行点乘并输出，其中值矩阵也是由输入特征图经过1×1 卷积计算得到。而本文设计的唯一不同之处在于，键值矩阵（key）和值矩阵（value）来自一个较大尺度的点云数据，查询矩阵（query）来自一个较小尺度的点云数据。由于较小尺度点云是由较大尺度点云经过下采样得到的，其包含了原有点云的一部分几何结构信息，将这个小尺度点云作为查询矩阵来源，可以使自注意力模型更好地计算出原有点云的关键点位置，得到更好的注意力图从而提高表征能力。另外，采用不同的下采样方法也会对该注意力模块造成不同影响，在实验4.3.2 小节对比了采用不同的下采样方式在不同规模的点云上所产生的效果。

其次，为了让S1 实现同样的全局上下文信息聚合，采用了一种简单的注意力机制来处理点云数据S1。首先，S1 将输入到一个非线性卷积层并进行softmax 计算，得到的数据再与原始S1 进行点乘计算，得到的输出数据S1′代表经过处理后的S1 数据。这个过程可以用如下公式表示：

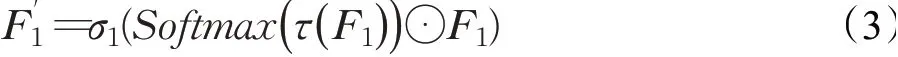
其中，⊙代表矩阵点乘，τ是用于生成注意力图的非线性卷积层，σ1的作用与σ0类似。这个结构设计思想来自于通道空间注意力模块（CBAM）[24]中的空间注意力模块，其能在空间维度上重新校准点云特征图，突出关键点信息。采用这个结构也能避免S0′和S1 两个点云数据之间的关键点信息差距过大导致难收敛的问题，从而提升预测精度。

这个模块增强了两个尺度点云数据的融合，解决了直接下采样导致点云数据之间的语义信息差异过大的问题，另外，由于对两个尺度的点云数据中都采用了注意力机制，增强了全局语义信息，从而提高了模型精度。在消融实验中也讨论了这个模块所带来的效果。一个完整的具有注意力机制的搜索单元如图4所示，经过基于注意力机制的多尺度融合模块处理后，得到新的S0 和S1 点云数据将作为两个输入节点传递到基于点卷积的候选操作组合模块，并输出最终数据。

3.3 基于点卷积的候选操作

为了解决点云处理效率问题，本文采用了基于点卷积的特征提取器组成候选操作（operations）。每个搜索单元中都包含以下5 种候选操作：MLP 点卷积核（相邻点数量设置为16、32、64），shell 点卷积核（层数设置为2、4，其中每层包含点数设置为16），恒同连接（skipconnect），空置操作（zero），1×1卷积。MLP点卷积核和shell 点卷积核是本文采用的面向三维点云的特征提取器，其他候选操作的功能则与面向图像数据方法中的类似。

不同于图像这种网格状的规则数据，三维点云是稀疏分布的，其中每个点包括了三维坐标( )x,y,z和语义特征值（比如RGB 值），在本文中用x∈RN×3表示每个点的三维坐标信息，用f∈RN×C代表上下文语意特征。为了减少一个深层神经网络的计算量，需要逐层地减少点云的数量。在本文中采用最远点采样（farthest point sample，FPS）[25]和随机采样（random point sample，RPS）来逐层减少点云数量，这类似于图像卷积神经网络中采用最大池化（max-pooling）等操作来逐层减少特征图的分辨率。FPS 算法会迭代地寻找与当前选择点相离最远的点，其计算复杂度为O(N2)。采用FPS 算法得到的下采样点云能保留更多的几何结构信息。RPS算法则是随机选择一定数量的点，其计算复杂度为O(N)，但对点云密度分布不平衡的情况十分敏感，适用于点数量较多的点云数据。这两种下采样算法将作为一个在搜索过程中的超参数，搜索算法将使用其中一种方式进行神经网络架构搜索。在实验4.3.2小节也对这个超参数进行了对比实验。

为了能让点卷积核更好地学习点云的局部特征，点云中的点需要聚合成多个点集，每个点集都会被输入到点卷积核中。由于点云数据通常规模较大，对近邻点聚合方法的计算效率有较高要求，目前点云处理领域中比较主流的近邻点聚合方法有K-最近邻点搜索（K-nearest neighbors，KNN）和球搜索（ball-query），文献[20]证明了采用球搜索方法会导致输入到卷积核中点的数量不稳定，从而影响模型收敛，而采用KNN能维持固定的点数量，使得模型能够获得更好的预测精度，而且KNN有更快的计算速度，因此在本文中也采用KNN 算法实现该近邻点聚合过程。

对于点卷积核，采用了基于多层感知机（MLP）的MLP点卷积核和基于可分离卷积的shell点卷积核两种。

MLP 点卷积核具有计算效率高的特点，而且由于MLP 能够拟合任意连续函数，所以这种点卷积核被证明有一定的特征提取能力[12]。借鉴了这个思路，本文重新设计了一种简单的MLP 点卷积核，其中包含了一个三层的全连接神经网络，输入层节点数和输出层节点数分别等于输入特征图和输出特征图的通道数。一个支持点p和其K-1个近邻点所构成点集为{x1,x2,…,xk},xi∈R3+C，则一个MLP 点卷积运算可以描述成如下的公式：

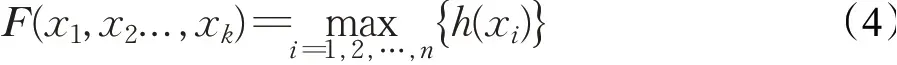
其中h代表全连接神经网络。具体流程如图5所示，对于第l层的点云中的某一个点集，将这个点集中所有点的上下文特征矩阵与对应的点云三维坐标矩阵（形状为[Nl+1,K,3]）进行拼接（concatenate），得到形状如[Nl+1,K,3+Cin]的矩阵，并将其输入到MLP 点卷积核中，得到形状如[Nl+1,Cout]的特征图矩阵，作为第l+1层的输入。由于点云的三维坐标与上下文信息是结合起来输入到MLP 点卷积核，所以MLP 点卷积核能够从中学习到三维坐标与上下文之间的关系。

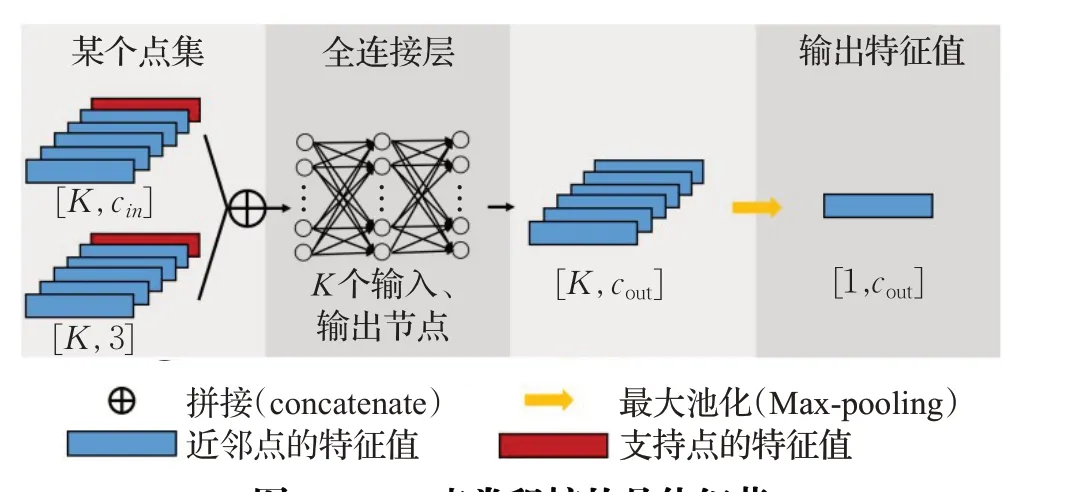
图5 MLP点卷积核的具体细节Fig.5 Details of MLP point convolution kernel

shell点卷积核则是使用了ShellNet[20]中的设计。在深层的卷积神经网络中通常会逐层地减少特征图分辨率，同时增加特征图的通道数，通过使用叠加卷积核的方法来获得足够大的感受野，MLP 点卷积核就是延续了这种想法，而shell点卷积核则是利用多个同心环区域划分不同权值，从而使用少量卷积核叠加即可获得足够大的感受野，具有一定的计算效率优势。

每个搜索单元中都包括了6 个节点（图4（b）），即3个中间节点，2个输入节点（输入数据为S0′和S1′）和1个输出节点，一个节点的数据会经过候选操作处理后输出给下一个节点。一个搜索单元的2 个输入节点的输入数据来自前两个搜索单元的输出，输出节点则是由所有中间节点的最终输出经过拼接得到的。

4 实验

4.1 在ModelNet10上进行神经网络架构搜索

4.1.1 实验数据集

ModelNet[9]系列数据集是一种三维点云分类任务数据集，其包括两个子数据集，即含有10个类别的Model-Net10 和含有40 个类别的ModelNet40。ModelNet10 含有4 899个物体模型的三维点云数据，其中包括3 991个测试样本和908个训练样本，对于每个模型的点云都将采样出固定的1 024个点。ModelNet40含有12 311个物体模型的三维点云数据，其中包括9 843 个训练样本和2 468个测试样本，同样对每个模型的点云都采样出固定的1 024个点。这里面的每个点都只包含了三维坐标。

本文延续了SGAS的搜索阶段的思路，即首先在小型数据集ModelNet10中搜索出一个包含正常单元和下采样单元的小型神经网络。然后采用增加通道数量和叠加多个单元的方式得到一个大型神经网络，作为面向大型数据集ModelNet40的模型。

4.1.2 参数设置

一个小型的神经网络有4个单元叠加而成，其中会在第1/3和2/3层的位置（即第1和第3层）使用下采样单元。正常单元中的点卷积核不会进行下采样计算，而下采样单元中的点卷积核则会进行下采样计算，经过下采样步骤之后，点数量减少至Nl，其中Nl=Nl-1/4，并且每个点的特征通道数将扩展成2 倍。这样设计的小型的神经网络相当于有4个层，而且第一层的特征通道数设定为32。

首先用ModelNet10小型数据集对这个小型神经网络进行训练。采用16 的批大小（batch size）训练40 遍（epochs），采用随机梯度下降（SGD）优化器来优化模型的权重W。采用Adam 优化器来优化网络参数A，A={α(i,j)}。需要注意的是对于SGAS搜索算法，本文只采用了第一种准则（Criterion 1）来选择操作o(i,j)，对于DARTS 搜索算法则延续文献[16]中的标准。本文的全部实验都在一个有11 GB显存的NVIDIA GTX 1080Ti显卡上进行。

4.1.3 实验结果

对于每一个搜索算法，都完成了10个独立的搜索过程，得到10个不同的小型神经网络，然后分别对小型神经网络中的单元进行叠加，得到10个大型神经网络，其中每个大型神经网络的单元数都由4个正常单元和2个下采样单元组成，并且第一层的特征通道数设定为48。批大小设定为16，并使用Adam 优化器训练80 epochs，且初始学习率为0.001，权值衰减（weight decay）为1×10-4。10 个大型神经网络在ModelNet10 数据集上的平均精度、最高精度以及与其他方法对比如表1 所示。相比一些经典的人工设计神经网络，本文提出的方法在这个小型数据集上有领先的准确率，而且采用SGAS 搜索算法在本文提出的搜索空间中搜索效果更好，相比用DARTS搜索算法的准确率提升了约0.6个百分点。

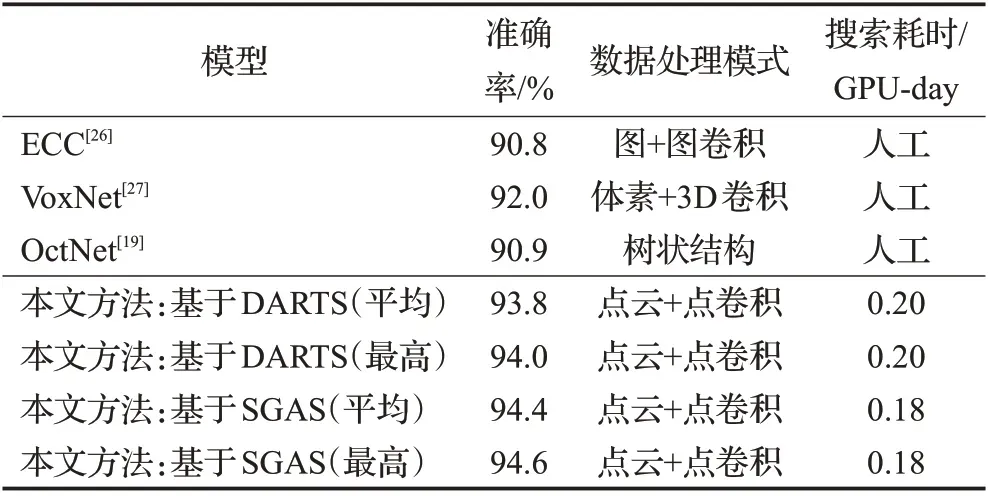
表1 分类任务数据集ModelNet10上的模型结果对比Table 1 Comparison of model results on classification task ModelNet10 dataset

4.2 在ModelNet40 上对搜索得到的神经网络进行验证

4.2.1 参数设置

这里只选择前面10个大型神经网络中最高精度的3个，并重新进行训练。批大小设定为16，使用Adam优化器训练150 epochs，且初始学习率为0.001，权值衰减（weight decay）为1×10-4。

4.2.2 实验结果

训练结果对比如表2所示，其中列出了4.2.1小节中选定的3 个大型神经网络在ModelNet40 数据集的测试样本集上的最高准确率和平均准确率，可以看到本文提出的基于SGAS搜索算法或者基于DARTS搜索算法都比其他一些人工设计的神经网络有更高的精度，说明本文提出的基于点卷积的搜索空间有一定的效果。同时，这些表现良好的大型神经网络都只用了0.18～0.20 个GPU-day（约4 h）即完成了神经网络构建的过程，相比人工设计和微调神经网络的方式，大幅减少了人力和时间成本。

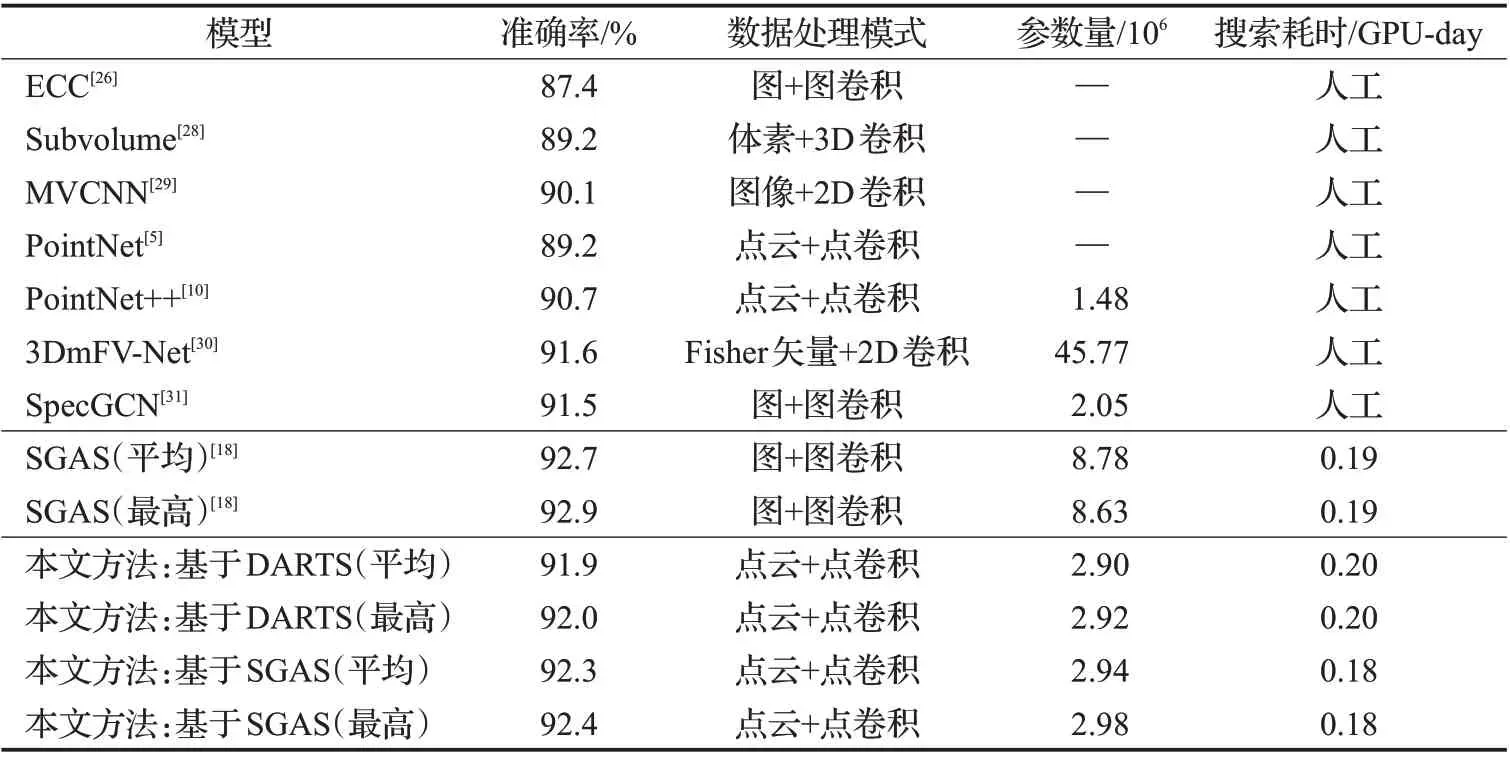
表2 分类任务数据集ModelNet40上的模型结果对比Table 2 Comparison of model results on classification task ModelNet40 dataset

采用SGAS 搜索算法在本文提出的基于点卷积的搜索空间进行搜索，相比基于图卷积的搜索空间（SGAS原文方法），其搜索耗时减少0.01个GPU-day（约0.24 h），搜索得到的网络可学习参数数量减少约70%，但准确率相比略低，可能的原因是本文使用的一些超参数（比如近邻点数量K、叠加的单元数量等）没有做详细的优化挑选。

本文提出了一种基于点卷积的搜索空间，可以采用任意基于可微分的搜索算法对其进行神经网络架构搜索，且采用不同的搜索算法得到的神经网络通常具有不同的收敛性。如图6和图7所展示的分别是采用两种搜索算法在ModelNet10和ModelNet40数据集上的训练验证曲线。从图6（b）和图7（b）可以看出，采用SGAS搜索算法得到的神经网络在两个数据集的验证集上均获得较低的误差，而且通过图6 和图7 可看出SGAS 得到的神经网络具有更快的收敛速度，即误差更早地降至最低水平。这是因为DARTS比较容易搜索出有较差表征能力的网络结构，而SGAS中以贪婪的方式逐步确定每个候选操作的方案则可以改善这种情况，而且根据在实验中的观察发现，采用SGAS得到的神经网络通常有更多的参数量，由于较复杂的网络结构通常有更好的泛化能力，所以采用SGAS得到的神经网络会有更高的准确率。另外，采用这两种搜索算法得到的神经网络都可以较好地收敛，表明本文提出的搜索空间具有一定的可行性。

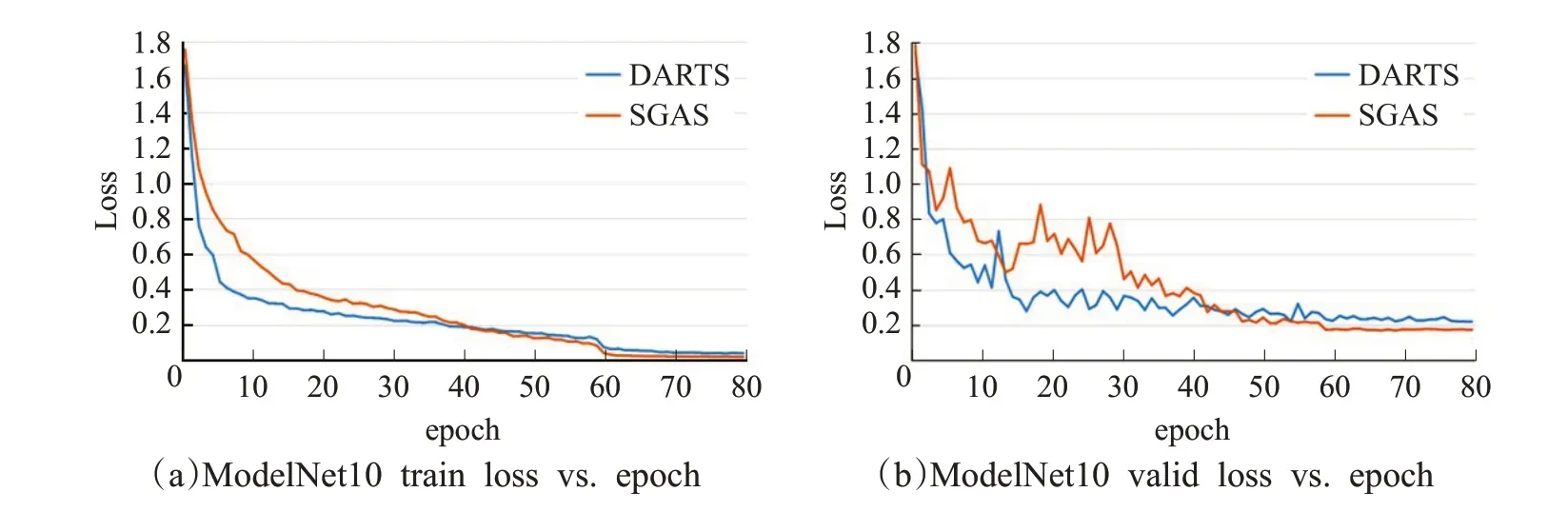
图6 在ModelNet10数据集上的训练和验证误差Fig.6 Train and valid loss on ModelNet10 dataset

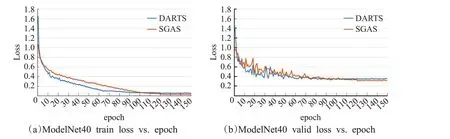
图7 在ModelNet40数据集上的训练和验证误差Fig.7 Train and valid loss on ModelNet40 dataset

4.3 在ModelNet40上进行消融实验

4.3.1 分析不同单元数和特征通道数的影响

由于构成一个神经网络的单元（cell）数和第一层特征通道数是人工设定的，为了观察这个设定对实验结果的影响，本文针对这两个超参数进行了消融实验。即是在搜索阶段，使用不同的单元数和第一层特征通道数组成小型神经网络，并使用SGAS搜索算法进行搜索。如表3 所示的是采用不同的单元数和第一层特征通道数进行神经网络搜索，最终得到的神经网络在Model-Net40数据集上的预测精度。可以看到随着单元数和通道数增加，搜索耗时也会随之增加，而且通道数对搜索耗时有更大的影响。其次，采用更多的单元和更多的特征通道数，搜索得到的神经网络具有更好的准确率，但需要留意的是，当通道数达到64时，准确率提升相比通道数为32 时变化不大，这表明小型神经网络的最优通道数是32。

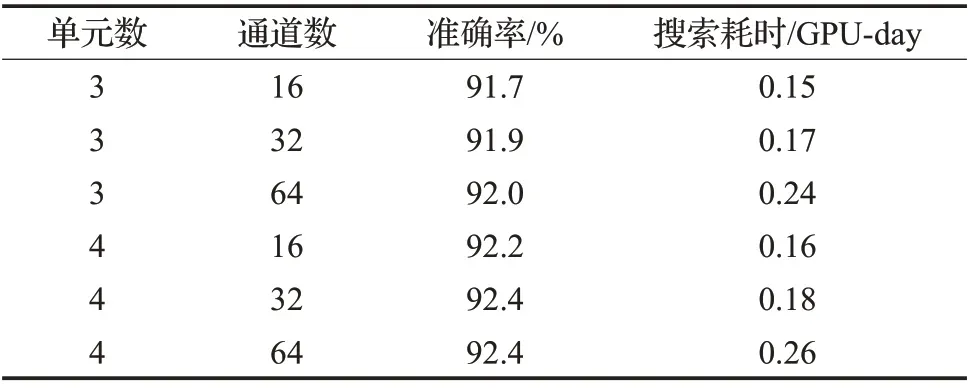
表3 由不同单元数和特征通道数搜索得到的神经网络对比Table 3 Comparison of neural networks searched by different number of cells and feature channels

4.3.2 不同的下采样方法效果对比

对于下采样方法，本文采用了最远点采样（FPS）和随机采样（RPS）两种，为了对比这两种下采样方法对模型的影响，在本实验中分别采用FPS和RPS组合成两种搜索空间，然后分别在不同点云数量的数据集中进行神经网络架构搜索，其他实验设定与4.1节和4.2节中的一致。最后验证搜索得到的神经网络性能，并对比其推断时间。

性能对比结果如图8 所示，在1 024 个点数量的点云数据中，采用RPS 方式得到的神经网络准确率为91.9%，而采用FPS 方式的准确率相比略高，为92.4%。随着点数量减少，采用RPS方式得到的神经网络准确率下降幅度不断增大，而采用FPS方式的准确率则是平稳下降。这是因为采用RPS 方式得到的点云很容易丢失几何信息，下采样率越大，对准确率影响也会不断加大。而经过FPS 得到的下采样点云仍能保留较准确的几何信息，采用这种下采样点云作为查询点（query），使得本文3.2节节中的注意力模块能更好地计算出原有点云中关键点的位置，从而更好地融合多尺度点云信息，提高预测精度。

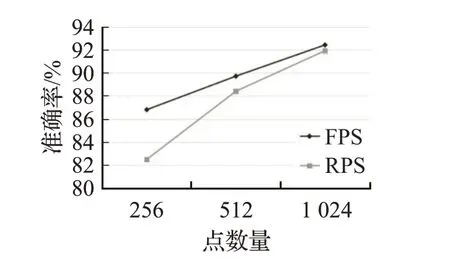
图8 采用RPS和FPS搜索到的神经网络性能对比Fig.8 Comparison of networks performance searched with RPS and FPS

推断时间对比如图9所示，相比采用RPS下采样的方式，采用FPS 的神经网络单个样本的推断时间多了4 ms，随着点数量减少，采用FPS 和RPS 两种方式之间的推断时间没有拉开较大差距，这是因为在整个神经网络中下采样的计算量占比不大，所以这两种方式没有表现出明显差距。

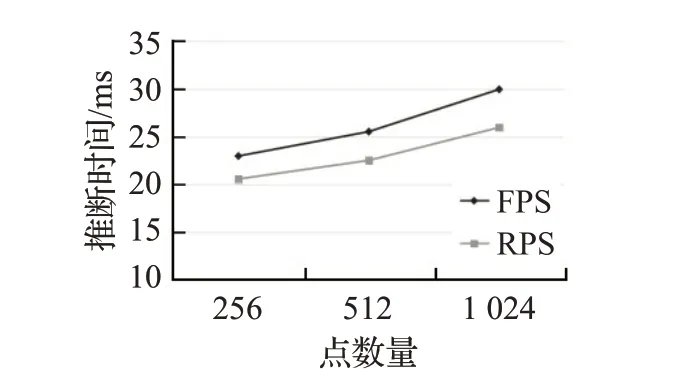
图9 采用RPS和FPS搜索到的神经网络推断时间对比Fig.9 Comparison of networks inference time searched with RPS and FPS

4.3.3 基于注意力机制的多尺度融合模块对比

为了让搜索单元能更好地融合两个不同尺度的输入点云数据，提出了一种基于注意力机制的多尺度融合模块。为了对比这个模块带来的性能提升，本文同样在ModelNet40 数据集上进行了消融实验，其中的基线模型采用类似于面向图像的搜索单元（图3），其结果如表4所示，相对于基线模型，加入了多尺度融合模块之后，可学习参数量增加了0.22×106，推断时间增加3 ms，准确率提升了1.1 个百分点，由此证明这个模块能带来一定的精度提升，同时不会增加过多的计算消耗。因为在一个神经网络中，只有下采样单元后面的一个普通单元中会采用多尺度融合模块，而整个神经网络只包含了两个下采样单元，所以多尺度融合模块也只计算了两次。另外，在多尺度融合模块中只有6个1×1 卷积具有可学习参数，总参数量与一个shell点卷积接近，所以加入多尺度融合模块所增加的计算消耗十分有限。

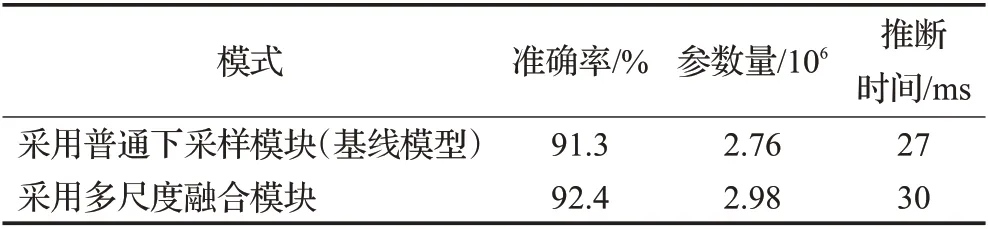
表4 基于注意力机制的多尺度融合模块的对比结果Table 4 Comparison results of attention mechanism-based multi-scale fusion module

4.3.4 采用不同候选操作的对比

本文采用了shell点卷积核和MLP点卷积核作为主要的特征提取器加入到候选操作组合中，为了对比这两个候选操作带来的性能提升，本文采用不同的候选操作组合重新进行网络架构搜索和训练验证过程，结果如表5 所示，其中基线模型是由恒同连接（skip-connect），空置操作（zero），1×1 卷积作为候选操作搜索得到的神经网络。可以看到基线模型的准确率很低，因为只有1×1卷积导致模型缺乏足够的特征提取能力。单独加入MLP点卷积核或者shell点卷积核都能带来一定的准确率提升，同时也能看出MLP 点卷积核的可学习参数量比shell点卷积核少。另外值得注意的是，单独加入shell点卷积核的可学习参数量比同时加入MLP点卷积核和shell 点卷积核的多，但准确率却有所下降，这是因为在神经网络中加入MLP点卷积核来替换一部分shell点卷积核，可以在减少神经网络参数量的同时增加网络结构的复杂度，一定程度上缓解过拟合的问题，从而提升准确率，这也证明了同时采用shell 点卷积核和MLP 点卷积核作为候选操作的必要性。

表5 由不同候选操作组合搜索得到的神经网络对比Table 5 Comparison of neural networks searched by different combinations of candidate operations

4.3.5 搜索结果可视化

经过搜索得到的神经网络由多个搜索单元叠加而成，其中搜索得到效果最优的搜索单元中的候选操作组合如图10 和图11 所示，需要注意的是因为基于注意力机制的多尺度融合模块是固定的结构，所以图中没有画出这一部分。mlpconv_k32 代表近邻点设置为32 的MLP 点卷积，shellconv_s2 代表近邻点为32 且含有2 层的shell 点卷积，shellconv_s4 代表近邻点为64 且含有4层的shell 点卷积，skip_connect 代表恒同连接。可以看到在下采样搜索单元中，shell 点卷积的数量占比较多，这是因为下采样过程通常需要更大的感受野，而shell点卷积相比MLP 点卷积拥有更大的感受野。另外，在一个神经网络中正常搜索单元数量更多，所以在正常搜索单元中具有更多的恒同连接（skip-connect）和1×1 卷积，这样能够在维持一定学习能力的同时减少神经网络参数量。

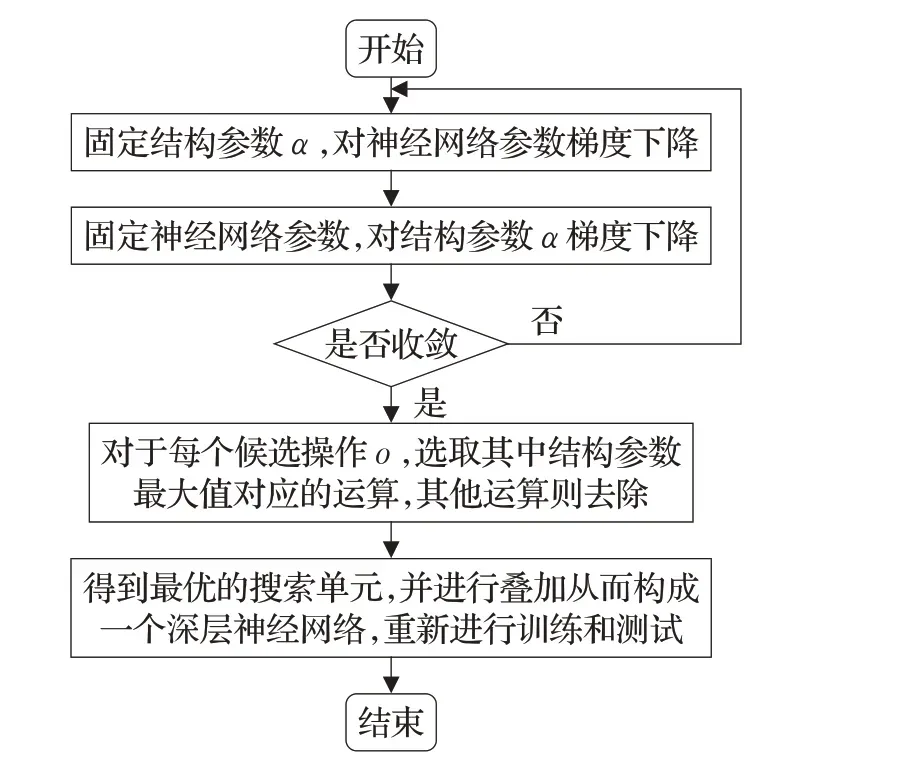
图1 DARTS搜索算法流程Fig.1 Process of DARTS search algorithm

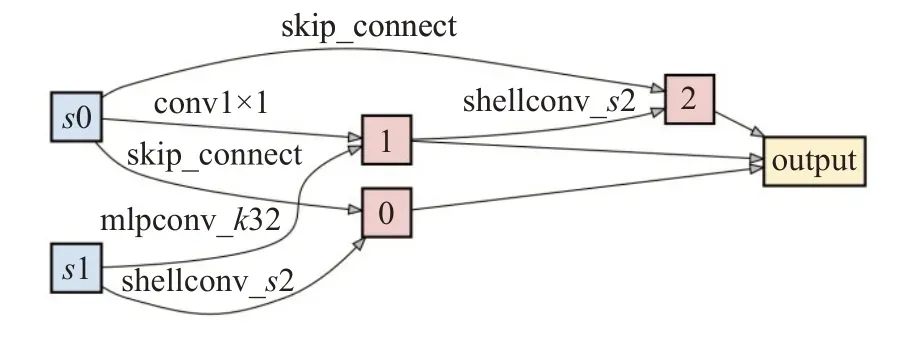
图10 正常搜索单元中的候选操作Fig.10 Candidate operations in normal search cell

图11 下采样搜索单元中的候选操作Fig.11 Candidate operations in subsample search cell

5 结束语

本文提出了一种面向三维点云的基于点卷积的搜索空间，组成该搜索空间的搜索单元中，包含了由MLP点卷积核和shell点卷积核构成的候选操作和一种基于注意力机制的多尺度点云融合模块。使用任意基于DARTS的搜索算法对这个搜索空间进行神经网络架构搜索，即可得到能直接处理原始三维点云的点卷积神经网络。本文借助了基于DARTS的搜索算法SGAS在一个小型三维点云数据集ModelNet10上进行神经网络架构搜索，最终得到基于点卷积的神经网络可以在大型三维点云数据集ModelNet40上获得比较领先的精度。同时在消融实验中证明了提出的多尺度融合模块能在基线模型上带来一定的精度提升。同样采用SGAS 搜索算法，相比在图卷积搜索空间中搜索神经网络的方式，在本文提出的点卷积搜索空间中搜索神经网络的方式能在维持相近精度的同时有更快的网络搜索速度，且搜索出的神经网络具有更少的可学习参数。由于整个搜索过程是全自动的，相比于人工设计神经网络的方法，本文提出的方法可以在很少的人工介入情况下，自动搜索出性能优秀的神经网络。关于后续的工作，计划是设计出更多的具有高计算效率的三维点云特征提取器，并作为候选操作加入到搜索空间中，以求搜索出的神经网络具有更高的特征提取能力，以及针对点云数据的特性继续对搜索空间进行优化。