基于多尺度特征和注意力的金融时序预测方法

詹 熙，潘志松，黎 维，张艳艳，白 玮，王彩玲

中国人民解放军陆军工程大学 指挥控制工程学院，南京 210007

股票市场被认为是一个国家或地区经济和金融活动的晴雨表，研究股票预测可以引导投资者进行有益的投资，这不仅可以为个人提供利润，还能对国民经济的发展做出贡献。然而，由于股票市场具有噪声和波动性的特点，准确地预测股价涨跌通常被认为是时间序列预测中最具挑战性的问题之一[1]。

近年来，金融领域广泛应用机器学习模型进行时间序列预测，支持向量回归（support vector regression，SVR）[2]和人工神经网络（artificial neural network，ANN）[3]在该领域取得了一定的效果。随着计算能力的发展，深度学习（deep learning，DL）技术成为了许多问题的最流行的解决方法。随着深度学习在计算机视觉[4-5]、语音识别[6-7]、自然语言处理[8-9]等领域取得的巨大成功，将深度学习运用在时间序列预测[10-11]等领域也逐渐受到关注。不像传统的基于统计的模型只能建模数据中的线性关系，深度神经网络在映射复杂的非线性特征交互方面有着巨大的潜力[12]。在过去的十几年里，计算能力的增加使得创建更深层次的模型成为可能。与浅层网络相比，模型层次的加深能提高它们的学习能力。与传统方法相比，深度学习方法无需任何预先假设就能直接适应数据，在处理只有少量统计信息的时间序列数据时具有显著优势，因此，深度学习与金融的结合具有非常广阔的前景。

长短时记忆（LSTM）网络和卷积神经网络（CNN）是当前最广泛使用的深度学习技术，LSTM模型的特殊结构设计使其可以有效地捕获序列模式信息，CNN 模型的特性使可以过滤掉输入数据中的噪声，提取对最终预测有价值的特征。因此，利用这两种深度学习技术优点的时间序列模型可以提高金融时间序列的预测性能。已经有研究表明，混合CNN 和LSTM 模型比单独使用CNN和LSTM更好[13]，但缺点是随着序列长度的增加，它们变得不再鲁棒，因为LSTM 难以捕捉长期依赖关系。金融时间序列预测面临的另一个问题是，在动态多变的环境下，当前存在的方法所提取的特征尺度较为单一，而在金融市场中，股价既会受到短期波动的影响，也会受到中期和长期趋势的影响，因此，仅使用单时间尺度的特征进行预测，会限制模型生成更加准确的预测结果。

为了解决上述问题，提高金融时间序列的预测精度，本文提出了一种新的融合扩张卷积网络DCNN和带注意力机制AT的基于长短期记忆网络LSTM的混合模型DCNN_LSTM_AT，该模型通过DCNN 和LSTM 从多时间序列中提取多尺度特征，并在此基础上使用注意力机制使模型聚焦于更重要的特征以提高预测精度。为了证明本文提出的DCNN_LSTM_AT模型的有效性，在来自国内外的多个股指数据集和个股数据集上进行了实验。实验结果表明，该模型能够有效提取和利用来自金融时间序列不同尺度的信息，从而达到提高金融时间序列预测精度的目的。

1 相关工作

自回归（auto-regression，AR）模型是由英国统计学家尤勒（Yule）提出的一个经典的时间序列预测模型，其输出值与历史值以及随机条件线性相关。后来，人们在这一经典模型的基础上，提出了其他改进的AR模型，如移动平均模型（moving average，MA）和自回归移动平均模型（auto-regression moving average，ARMA），虽然MA 和ARMA 模型有效地提高了在序列平稳假设条件下模型的预测精度，但由于现实世界中存在的时间序列主要是非平稳的，而上述模型不适用于非平稳时间序列数据，因此Box 等人[14]提出了差分自回归移动平均模型（auto-regression integrated moving average，ARIMA）。ARIMA通过差分使时间序列数据变得平稳，但差分运算通常会放大时间序列数据中的高频噪声，从而影响预测精度，为了缓解这一缺陷，Peter 等人[15]基于ARIMA 提出了具有外部输入的ARIMA 模型来处理时间序列数据，以达到提高时间序列预测精度的目的。

另一些流行的时间序列预测模型是基于神经网络的模型，根据通用逼近定理，神经网络可以以任意精度将任意波雷尔（Borel）可测函数从一个有限维空间逼近到另一个有限维空间[16]，因而神经网络模型在解决非线性问题方面具有很大的优势。Hamzaçebi 等人[17]提出了一种基于神经网络的时间序列预测方法，取得了比ARIMA 等模型更好的效果，但精度仍有待提高。Naduvil 等人[18]提出了一种ARIMA 模型与神经网络相结合的混合时间序列预测模型，该混合模型利用ARIMA 模型对线性数据的优秀拟合能力和神经网络对非线性数据的优秀拟合能力，使其在时间序列数据上获得了较好的预测精度。

近年来，随着计算能力的提升，深度模型逐渐被用于时间序列预测任务中，Connor等人[19]提出了递归神经网络（recurrent neural network，RNN），它利用时间序列的历史信息来预测未来的结果，但随着序列的增长，其在训练的过程中会遇到梯度消失和爆炸的问题。Hochreiter等人[20]提出了一种改进的RNN模型LSTM用于时间序列预测，通过多个门机制缓解梯度消失和爆炸问题，使其成为了时间序列预测中最常见的基础模型之一。在此基础上，Yan 等人[21]建立了基于LSTM 深度神经网络的金融市场时间序列高精度短期预测模型，并与神经网络、传统RNN 和改进的LSTM 深度神经网络进行了比较，实验结果表明，LSTM 深度神经网络具有较高的预测精度，能够有效预测股票市场的时间序列。卷积神经网络（convolutional neural network，CNN）最初是为计算机视觉任务而设计的网络结构，CNN 使用卷积运算从原始数据中提取有意义的特征，卷积运算是一种滑动滤波器，用于创建特征映射，旨在捕获数据不同区域的重复模式，这种特征提取过程为CNN 提供了一种重要的特性，即失真不变性，这意味着无论特征在数据中的位置如何，都可以提取特征。这些特性使得CNN同样适合处理时序数据。Shen等人[22]利用CNN对金融时间序列进行预测，通过实验证明了CNN 也可以预测时间序列。Lu等人[23]结合CNN和LSTM提出了一种混合模型对金融时间序列进行预测，相比于单个模型，其预测精度有一定的提升，但该方法主要提取时间序列中相对单一的尺度特征进行预测，而在金融市场中，股价既会受到短期波动的影响，也会受到中期和长期趋势的影响，因此，仅使用单时间尺度的特征进行预测，会限制模型生成更加准确的预测结果。

与上述方法相比，本文所提方法不使用固定的时间间隔来建模时间序列，相反，该方法使用LSTM 和DCNN从时间序列中提取具有不同时间尺度的特征，并基于注意力机制使模型聚焦于重要特征，通过充分利用金融时间序列中的有效特征，达到提高模型的预测精度的目的。

2 DCNN_LSTM_AT模型原理

在具体的介绍DCNN_LSTM_AT模型之前，本文首先形式化地介绍所研究的股指收盘价预测问题，接着系统地介绍一下DCNN_LSTM_AT 模型，最后再介绍DCNN_LSTM_AT模型所包含的各个组成部分。

2.1 股市收盘价预测问题

2.2 DCNN_LSTM_AT模型总体框架

本文所提出的DCNN_LSTM_AT 模型如图1 所示，从功能上，该模型可以分为两部分：第一部分是扩张卷积网DCNN 与LSTM 组成的Encoder，其功能在于提取时间序列不同尺度的信息；第二部分是基于LSTM和注意力机制AT的Decoder，其功能在于有效利用第一部分提取的信息进行预测。从结构上看，该模型可以分为三个部分：第一部分是扩张卷积模块；第二部分是LSTM编码模块；第三部分由注意力机制AT 和LSTM 解码器构成解码模块。

由图1 可以看出，对于给定的序列数据x1,x2,…,xt-1,xt，其分别被输入到基于DCNN 的编码器和基于LSTM的编码器中，提取来自原始时间序列数据不同时间尺度的隐藏特征H1 和H2，接着H1 和H2 被合并为H，以备后续基于注意力机制和LSTM 的解码过程使用。接下来本文从结构上详细介绍DCNN_LSTM_AT模型。

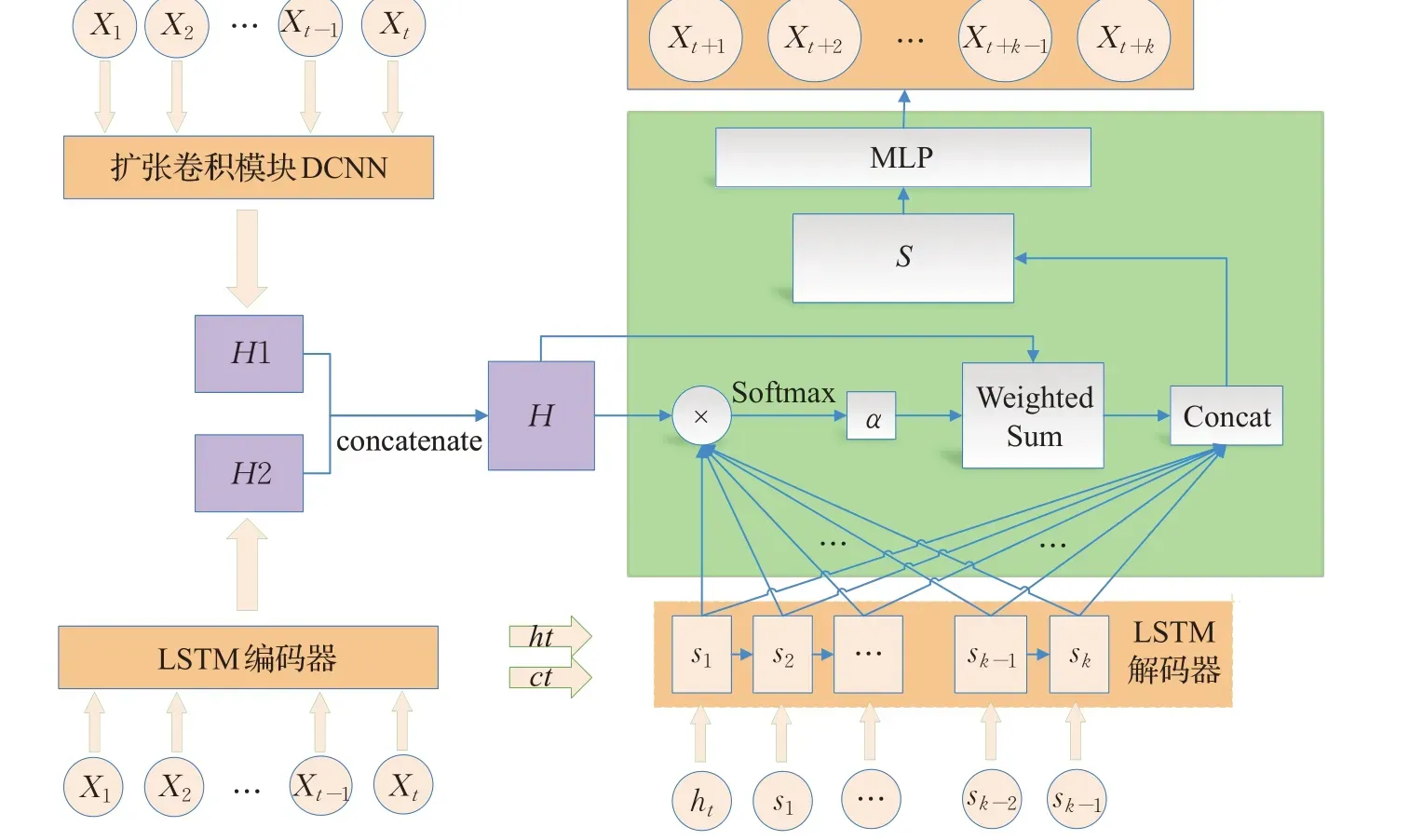
图1 DCNN_LSTM_AT模型的整体结构图Fig.1 Overall structure of DCNN_LSTM_AT model

2.3 DCNN_LSTM_AT模型组成

2.3.1 扩张卷积神经网络模块（DCNN）

DCNN模块是由多个扩张卷积网络堆叠而成的，扩张卷积是文献[24]中提出的卷积模块。有研究表明，在处理时间序列预测任务时，使用了池化操作的CNN 会降低预测的性能[25]，这是因为在池化操作的过程中，虽然扩大了对于原始输入序列数据的感受野，但与此同时也会导致相当一部分特征的损失。而对于普通的CNN来说，倘若其不使用池化层，其想要达到感受野大小与使用了池化层的CNN 的相同，需要更多的卷积层或者扩大卷积核，这样势必会造成计算负担，同时前者也将更容易导致梯度消失或梯度爆炸等问题。因此为了能够增加感受野的同时不损失信息，扩张卷积是一个很好的选择。扩张卷积通过增加扩张率来扩大感受野，感受野随着扩张率的增加而增大的示意图如图2所示。

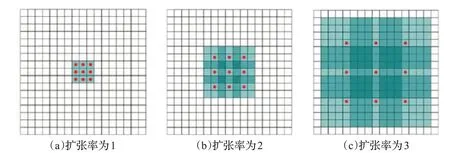
图2 扩张卷积在不同卷积率下的示意图Fig.2 Schematic diagram of dilated convolution at different convolution rates

本文中使用的DCNN模块的具体结构如图3所示，由图3可以看出DCNN由K个残差块连接而成，其中每个残差块都包括了一个扩张卷积层和一个1×1卷积层，在每个残差块中，加入了Batch Norm层，目的是为了加快模型的收敛速度，此外还使用了残差连接和跳跃连接；在网络构建过程中，本文通过堆叠残差块和增加扩张卷积的扩张率使得模型逐渐拥有更大的感受野，其中对于第K个残差块而言，其扩张率为2K-1，这样每个残差块将能提取不同时间尺度的序列特征，图3所示的模型最终将提取K条具有不同时间尺度的序列特征，最后合并成H1。

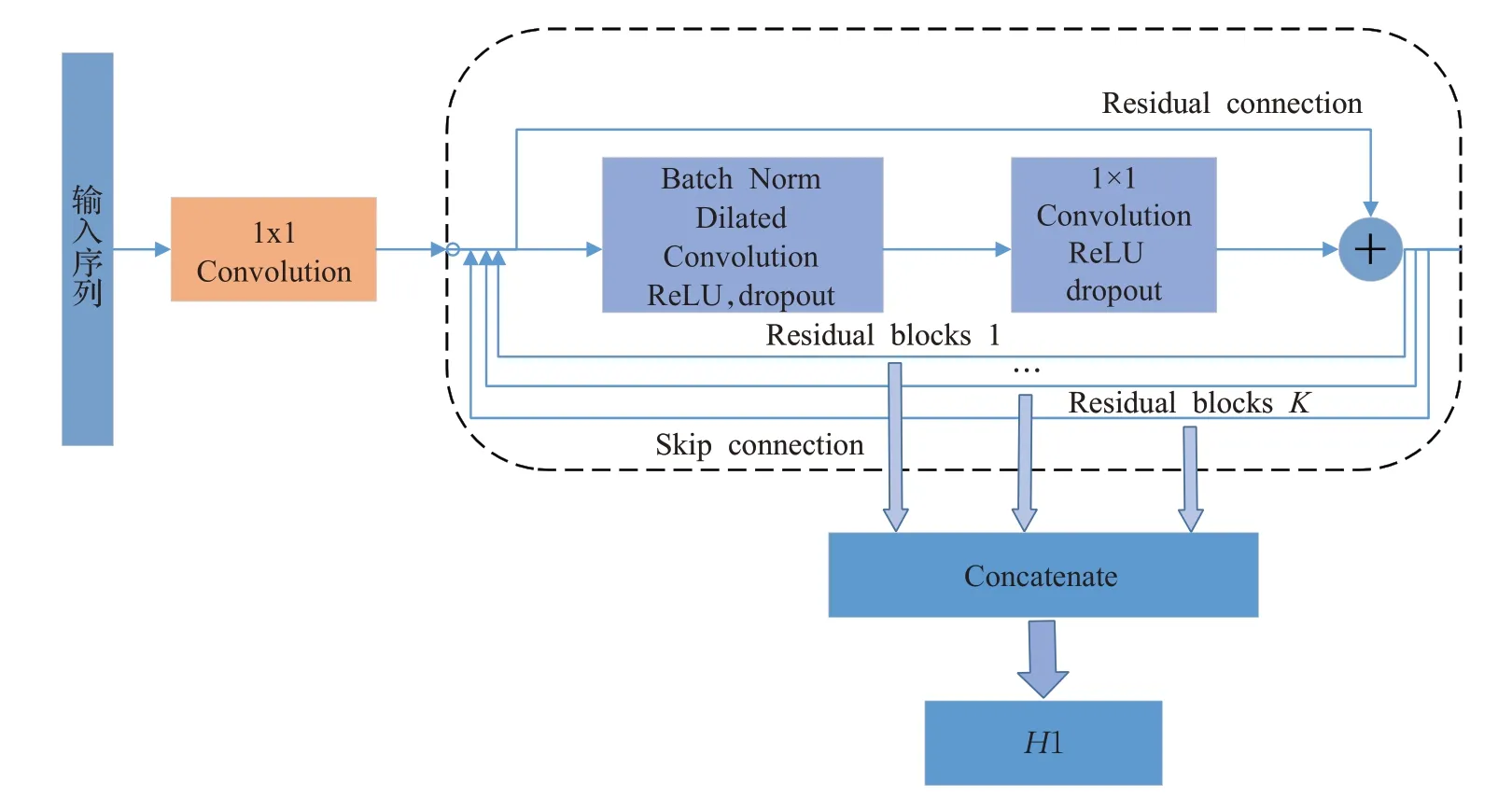
图3 扩张卷积网络模块的具体结构图Fig.3 Specific structure diagram of dilated convolutional network module

2.3.2 LSTM编码模块

与传统的人工神经网络相比，递归神经网络可以利用时间序列数据的历史信息来构造特殊的网络结构。RNN 能够根据当前和过去的输入生成输出数据。然而，当使用梯度下降算法来训练RNN 网络时，容易出现梯度消失或梯度爆炸现象[26]。序列越长，可能性越大，这使得很难对RNN 进行长时间间隔的有效训练。为了解决这个问题，人们提出了递归神经网络的其他变体，以便容易地捕获长期依赖性，如LSTM和GRU。

LSTM 是学习原始时间序列数据的长时间相关性特征的一种流行的RNN变体，LSTM的单元结构如图4所示。

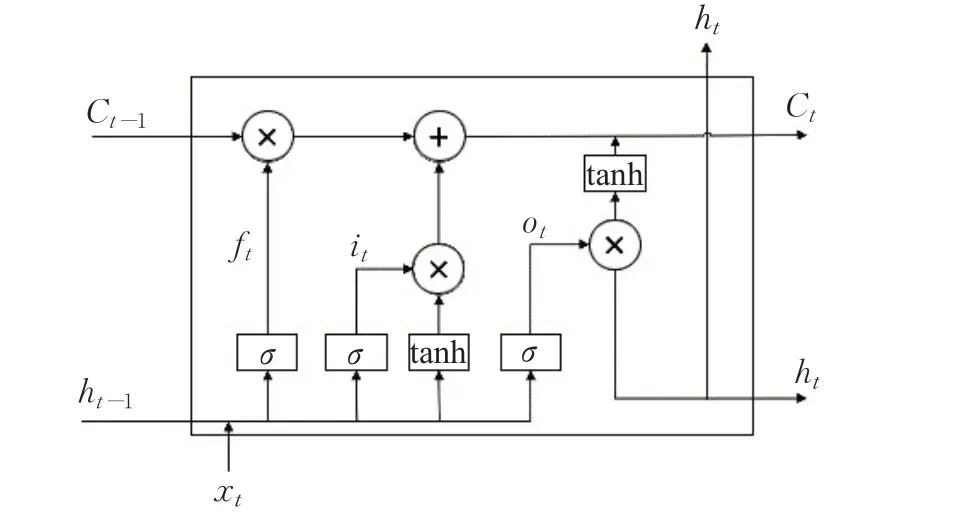
图4 LSTM Cell内部结构图Fig.4 Internal structure diagram of LSTM Cell

LSTM 单元使用3 个门：遗忘门、输入门和输出门，来控制隐藏层存储的历史信息，LSTM 单元在时间点t的公式如下所示：

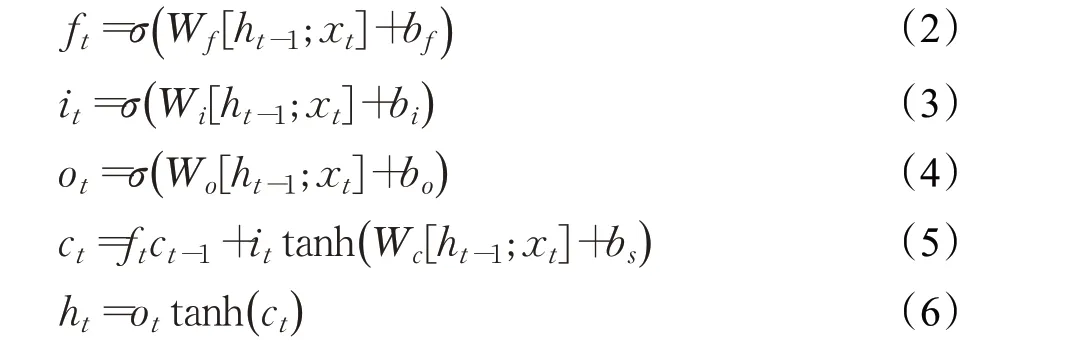
本文结合LSTM 对序列数据建模和捕获长期依赖性的优点，使用LSTM为基本单元构成的编码器提取输入序列的整体特征。

2.3.3 注意力机制和LSTM解码器构成的解码模块

注意力机制是从认知心理学中引入的一种模拟人脑注意的模型，从概念上讲，注意力机制在原理上与人类的视觉注意机制非常相似，是一种从海量信息中快速锁定关键信息，消除无用信息，更高效地完成任务的方法。如图5所示，注意力机制主要通过计算输入和目标状态之间的相似性来完成上述功能，相似度越高，当前输入的权重就越大。在图5 中，Z是目标状态，ht是LSTM单元的隐藏状态，at定义为每个输出应考虑多少输入状态的权重。Match是一个函数，用于计算向量Z和ht之间的相似性，Match可以使用任何理论上计算相似性的方法，例如余弦相似性，或矩阵变换at=ht*W*Z，或以ht作为输入，at作为输出的简单神经网络。

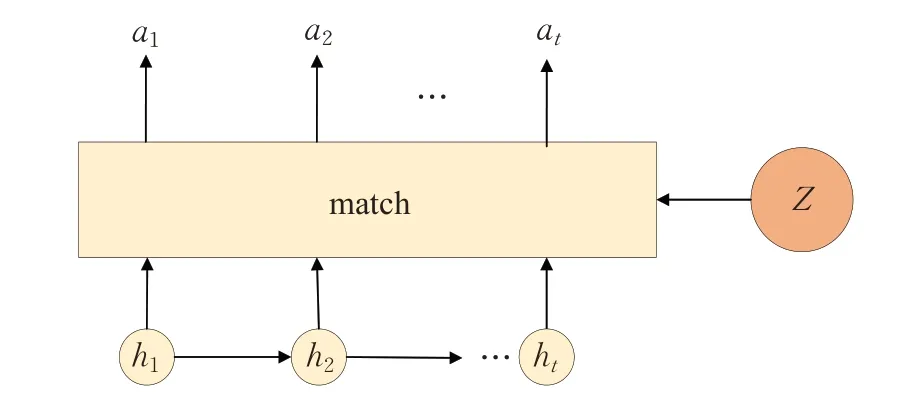
图5 注意力机制示意图Fig.5 Schematic diagram of attention mechanism

具体的，本文所使用的注意力机制如图1中的绿色区域所示，在本文所使用的注意力机制中，通过将扩张卷积网络模块所提取的多尺度特征H1 同基于LSTM的编码器所提取的整体特征H2 合并成H后，将H同基于LSTM 的解码器第i个单元所输出的第i条特征Si,i=1,2,…,k进行乘积运算得到重要性得分Score，接着对得到的Score 使用Softmax 函数进行归一化得到归一化后的重要性权重α，然后令α与H相乘之后按列求和，再将得到的结果同Si合并，一同送入到全连接层中，最后输出预测结果，上述过程的公式化描述如下所示：

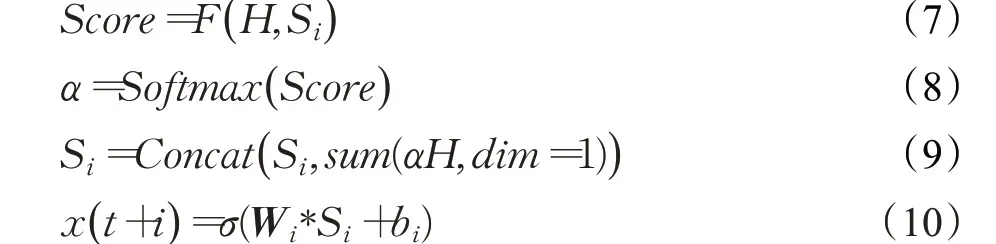
其中，式（9）中的Concat代表合并操作，sum(αH,dim=1)代表对αH在维度1上进行求和，式（10）中的σ、Wi和bi分别代表全连接层的激活函数、权重向量以及偏置值。

3 实验

3.1 实验数据集

为了评估所提模型的性能，本文分别在沪深300、标普500 以及富时100 等指数数据集，以及茅台、Apple 和中信银行等国内外上市公司的个股数据集上进行了实验，其中股指数据集包含了截止到2021 年5 月10 日为止的2 500 个交易日的数据，个股数据集包含了截止到2021年5月28日为止的2 500个交易日的数据，此外，本文选取了开盘价、最高价、最低价、交易量和收盘价这5个指标作为模型的输入特征，并使用包含这5个特征的历史数据来预测未来的收盘价。

3.2 数据处理

为了评估本文所提出的模型，将所有数据集分为训练集和测试集，其中训练集包含2 200个交易日的数据，测试集包含300 个交易日的数据。不同数据集划分情况如表1所示。

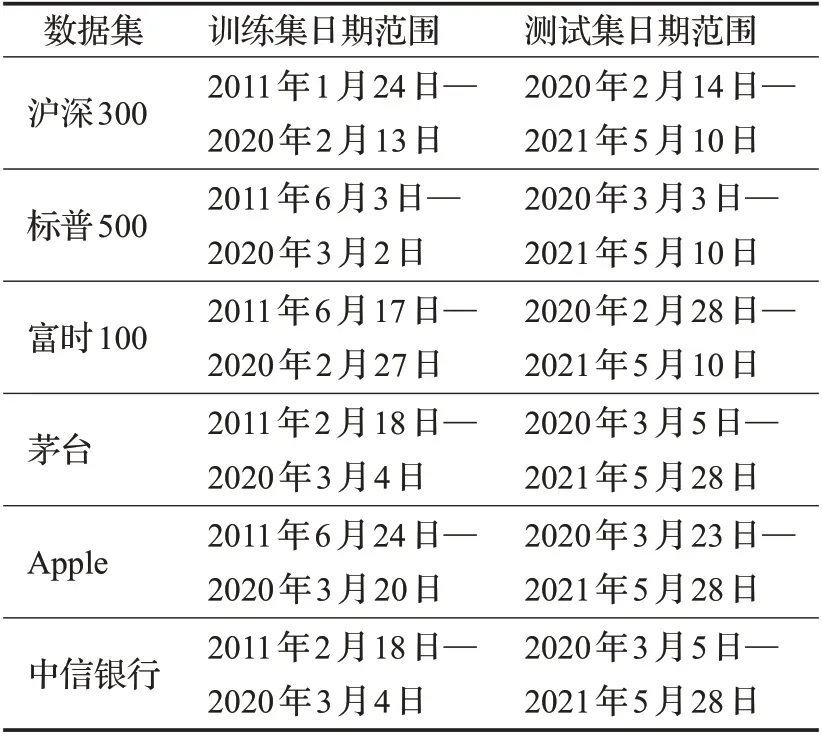
表1 不同数据集中训练集和测试集的时间范围Table 1 Time range of train and test sets in different datasets

需要说明的是，由于各个国家的节假日不相同，这会导致股市的开市时间不一致，因此相同数量交易日的间隔日期也不一样。时间序列划分被为训练集和测试集之后，将执行以下预处理操作：首先，使用滑动窗口法将时间序列分割为一个个的训练样本以供模型训练，这个过程通过滑动一个固定大小的窗口，滑动窗移动的过程中在每个位置产生一个输入-输出样本；其次，使用MinMax归一化法，将划窗后训练集中的每个输入-输出样本对的值映射到0 和1 之间，这样有助于加快网络的收敛速度。

如图6展示了滑动窗口确定输入-输出样本的过程，这里取4作为输出窗口的长度，也就是预测范围，取5作为输入窗口的长度，这样截取下来的输入输出窗口对就成了一个带标签的样本对，输出窗口中的值为标签，输入窗口中的值为输入特征。

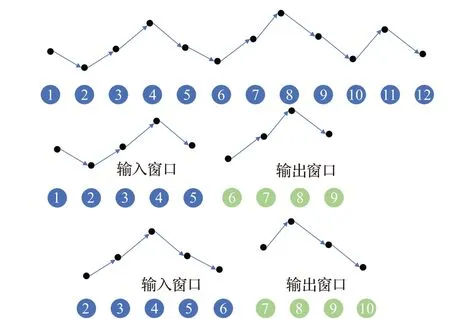
图6 样本滑窗示意图Fig.6 Schematic diagram of sample sliding window

3.3 评价指标

本文使用了3 个评价指标来评估本文所提出的模型，分别是平均绝对误差（mean absolute error，MAE）和平均绝对百分比误差（mean absolute percentage error，MAPE）和决定系数（coefficient of determination，R2），其中MAPE因其在尺度独立性上的优势，是预测精度最广泛使用的指标之一[25]；MAE 是相对较经典的一种度量指标，该指标对于预测的离群值比较敏感，能够有效衡量模型的稳定性；R2 反映了因变量的全部变异能通过回归关系被自变量解释的比例，是回归任务中常见的一种评价指标。上述3种指标的公式如下所示：

3.4 实验结果与分析

DCNN_LSTM_AT 模型在训练过程中，batch_size、残差块的数量以及学习率分别被设置为64、8 以及0.001，本文选择使用Adam优化器对网络参数进行优化和均方误差损失函数训练模型，均方误差损失函数公式如下所示：

为了验证本文所提模型DCNN_LSTM_AT的性能，本文在沪深300、标普500 以及富时100 等股指数据集和茅台、Apple以及中信银行等个股数据集上测试了DCNN_LSTM_AT模型，并与LSTM、ESN[27]、CNN、Transformer[28]、LSTNet[29]等基准模型在上述6 个金融时间序列数据集上进行了对比实验，其中LSTM、ESN、CNN等模型的参数设置参考了文献[25]中总结的各个模型在相同数据集上表现最好的参数设置，Transformer 和LSTNet 模型的参数设置分别参考了文献[28]和[29]中的设置，上述基准模型的训练轮数、学习率等超参数的设置均与DCNN_LSTM_AT 模型的设置保持一致。各个模型的对比实验效果如图7～12 所示，相关评价指标的详细结果见表2和表3所示。从预测效果的对比图和评价指标可以看出，本文所提模型DCNN_LSTM_AT 的表现在6个数据集中均超过了其他方法，整体上预测误差最小、预测值与真实值最为接近，这表明本文所提方法有效提高了金融时间序列的预测精度，且DCNN_LSTM_AT模型在金融时间序列领域具有一定的可扩展性。

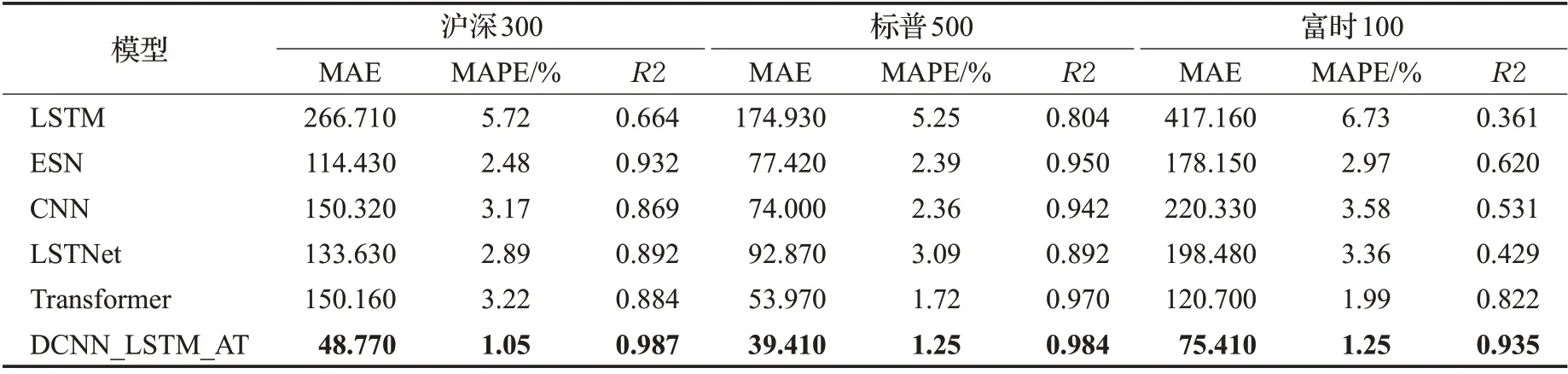
表2 DCNN_LSTM_AT与其他基准模型在股指数据集上的表现Table 2 Performance of DCNN_LSTM_AT and other benchmark models on stock index datasets

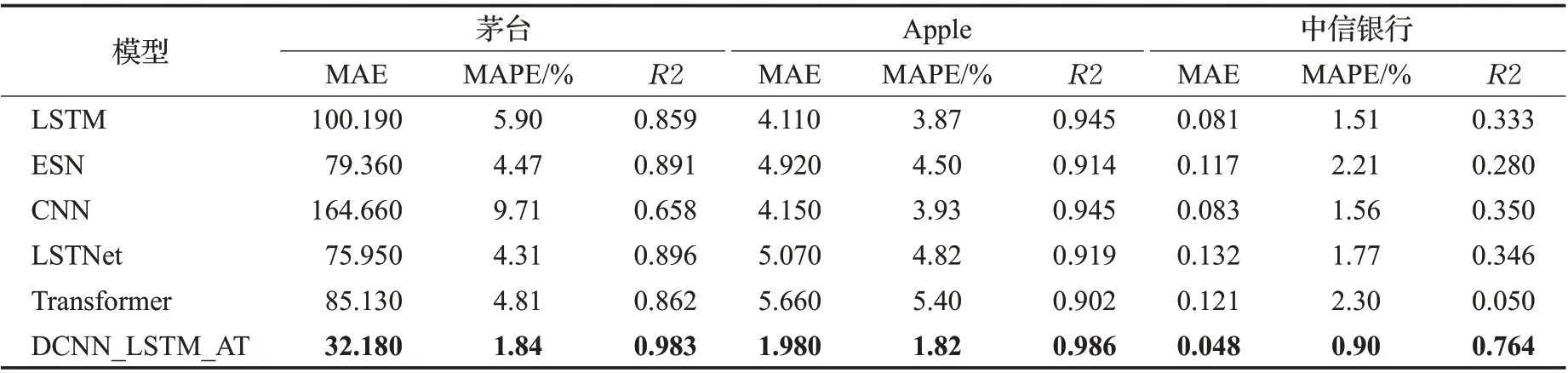
表3 DCNN_LSTM_AT与其他基准模型在个股数据集上的表现Table 3 Performance of DCNN_LSTM_AT and other benchmark models on datasets of individual stocks

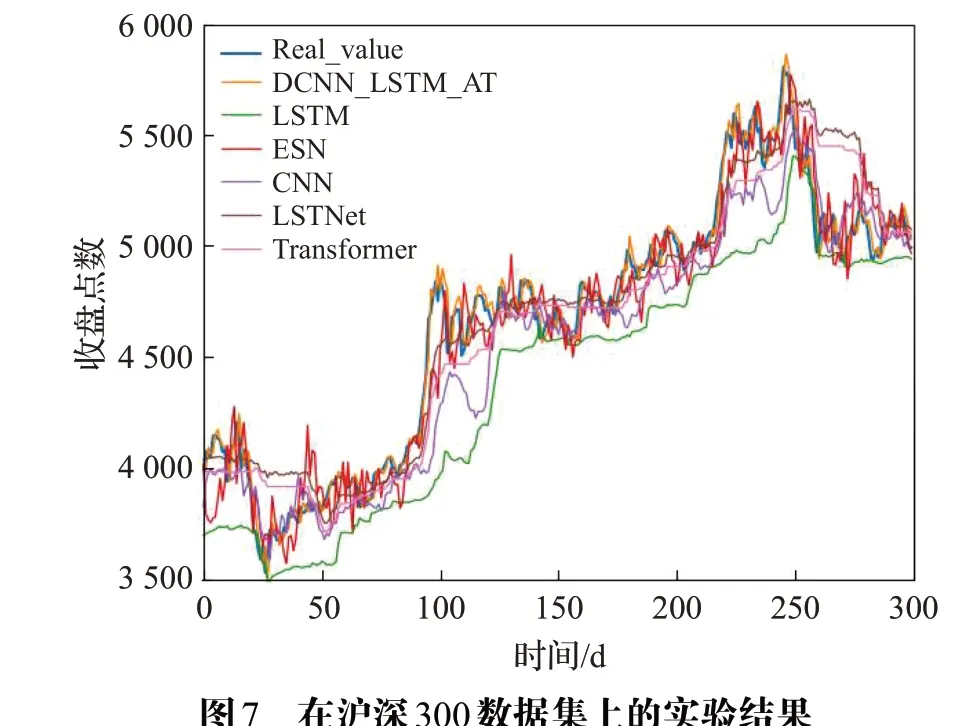
图7 在沪深300数据集上的实验结果Fig.7 Experimental results on CSI 300 dataset

为了验证本文提出的模型DCNN_LSTM_AT 所使用的扩张卷积神经网络的有效性，本文构造了LSTM_AT模型，与DCNN_LSTM_AT 模型的不同之处在于没有使用DCNN 提取时间序列的多尺度特征；为了验证所提出模型使用的注意力机制的有效性，本文构造了DCNN_LSTM模型，与DCNN_LSTM_AT的不同之处在于，其没有使用注意力机制；为了验证本文所提出的使用不同卷积率的扩张卷积的有效性，本文构造了模型CNN_LSTM_AT，其与DCNN_LSTM_AT的不同之处在于其在每个残差块中使用了同一大小的卷积核。随后本文分别比较了DCNN_LSTM_AT 与其他三个模型在沪深300、标普500 以及富时100 股指数据集上的预测表现，在实验过程中，所有对比模型的超参数均与DCNN_LSTM_AT模型的设置保持一致，最终的实验结果如图13～15所示。

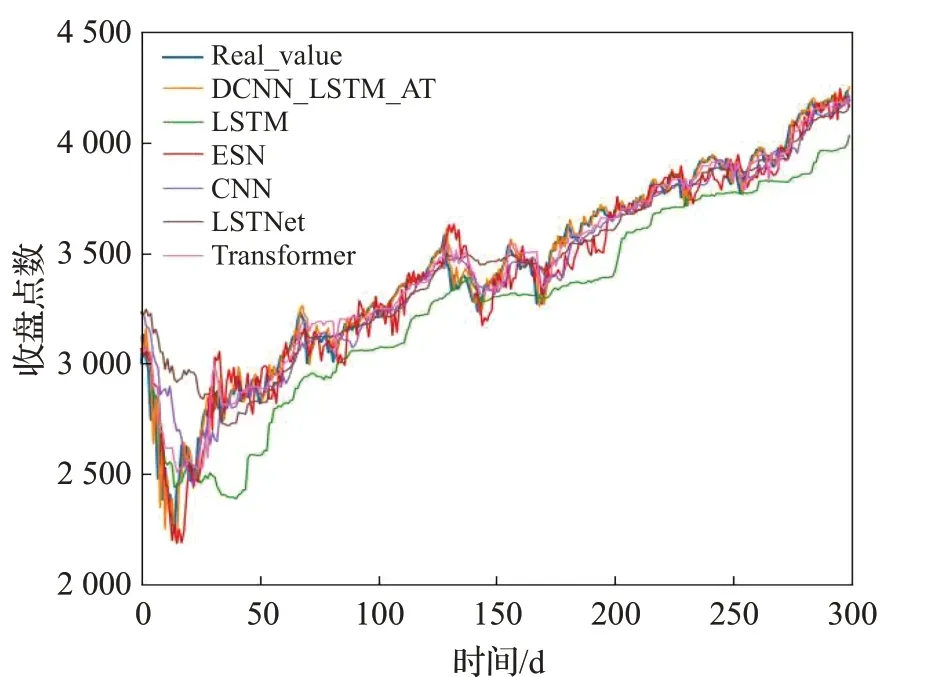
图8 在标普500数据集上的实验结果Fig.8 Experimental results on S&P 500 dataset

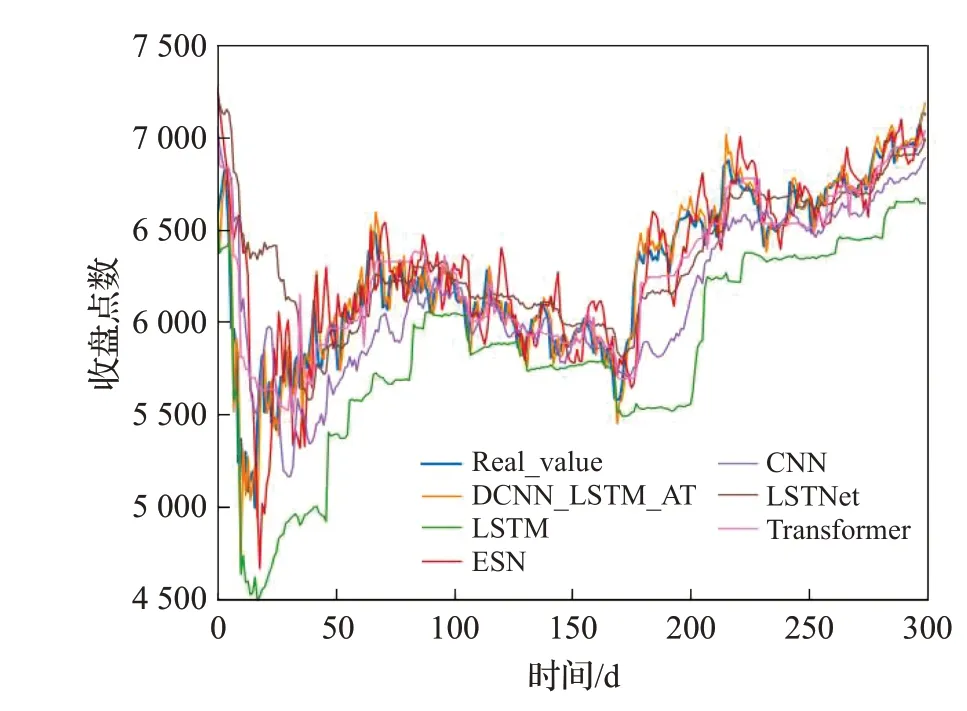
图9 在富时100数据集上的结果Fig.9 Experimental results on FTSE 100 dataset

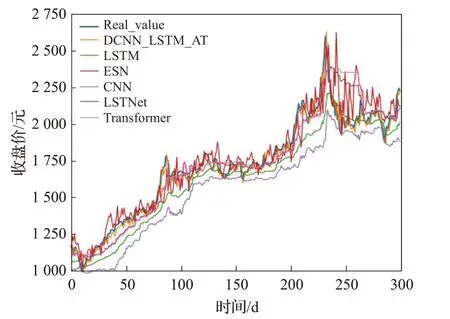
图10 在茅台数据集上的实验结果Fig.10 Experimental results on Maotai dataset

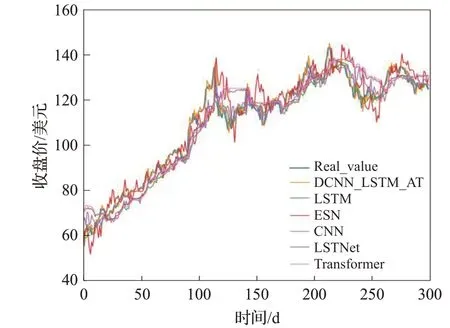
图11 在Apple数据集上的实验结果Fig.11 Experimental results on Apple dataset

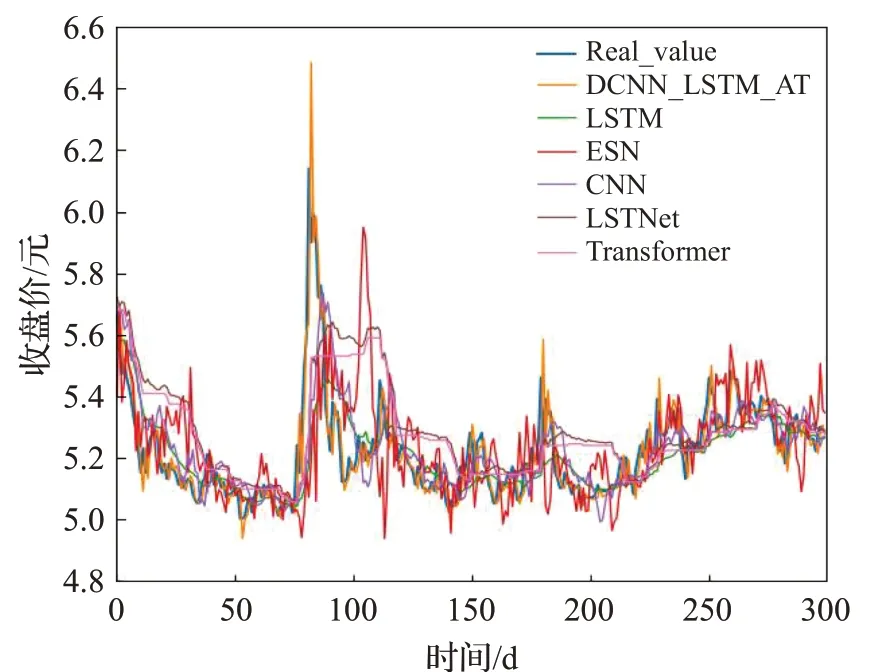
图12 在中信银行数据集上的实验结果Fig.12 Experimental results on CITIC Bank dataset

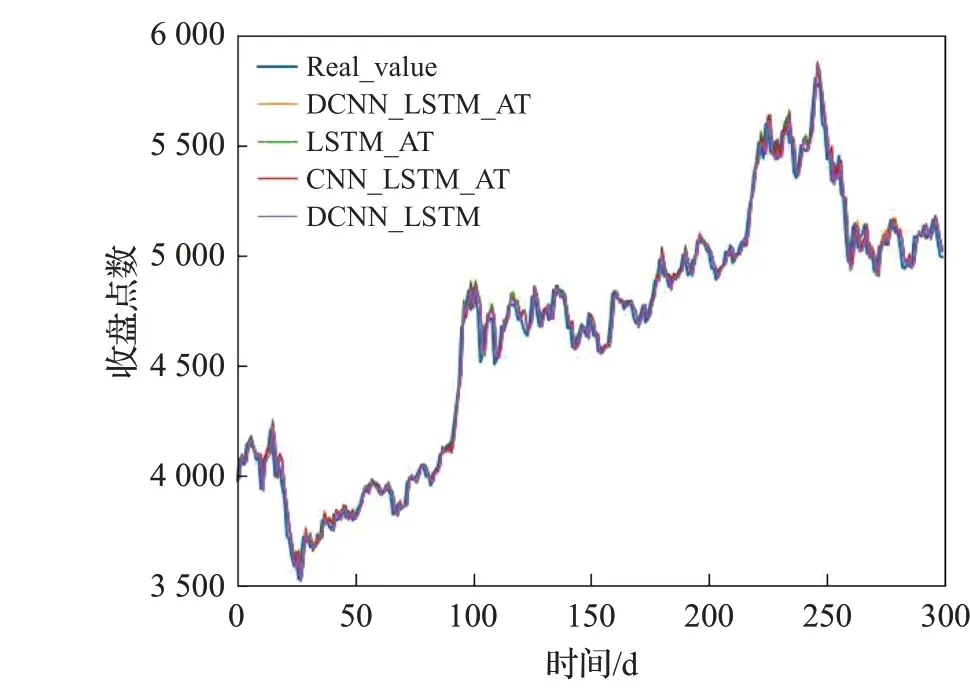
图13 构造模型在沪深300数据集上的实验结果Fig.13 Experimental results of constructed model on CSI 300 dataset

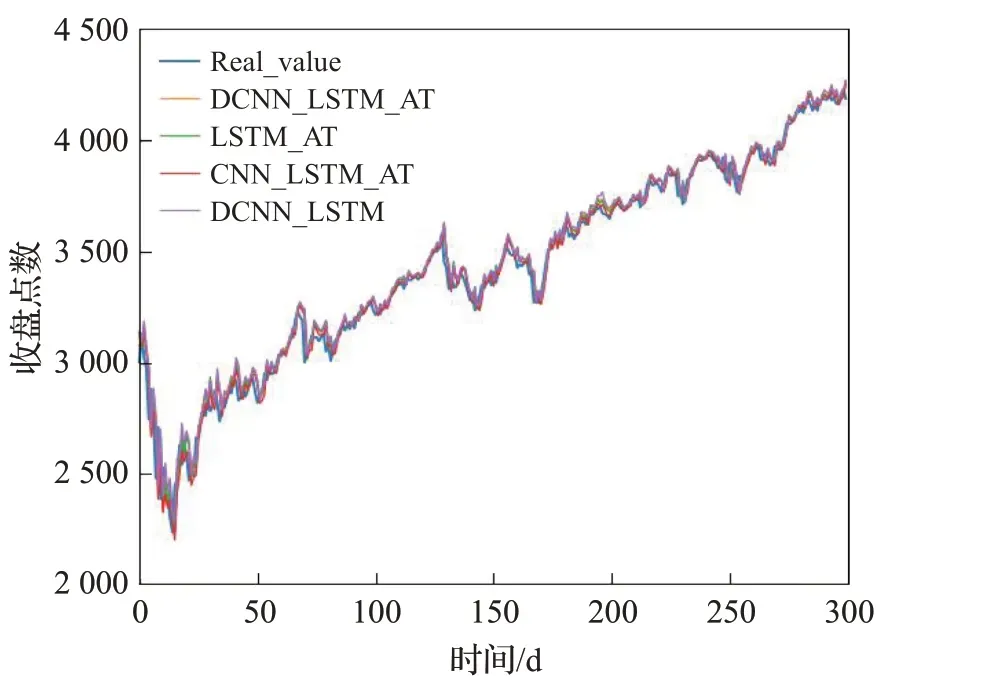
图14 构造模型在标普500数据集上的实验结果Fig.14 Experimental results of constructed model on S&P 500 dataset

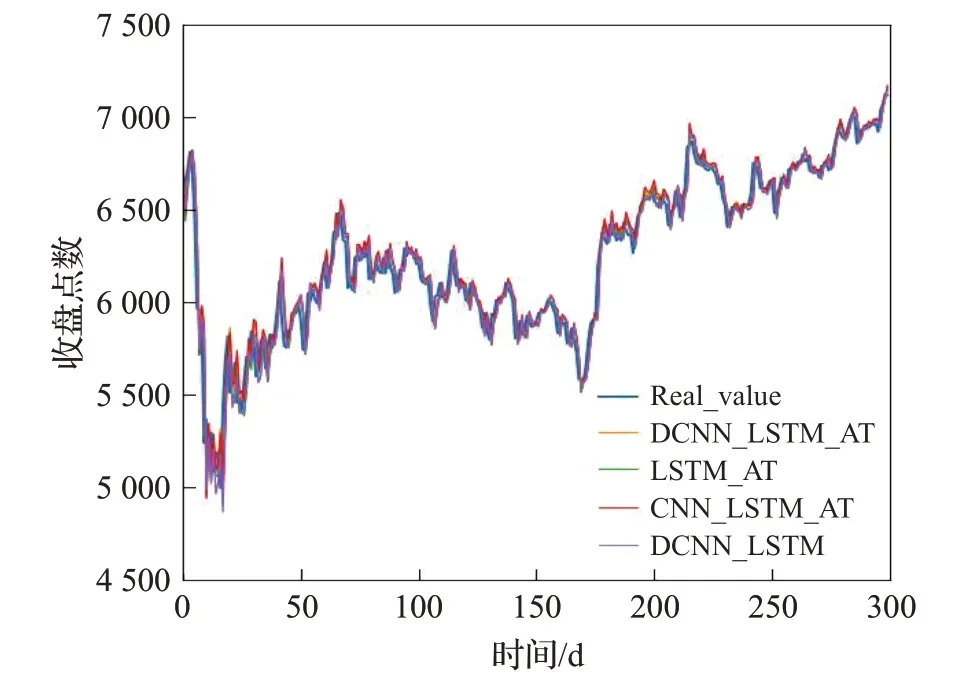
图15 构造模型在富时100数据集上的实验结果Fig.15 Experimental results of constructed model on FTSE 100 dataset

表4给出了上述4个模型在沪深300、标普500以及富时100 等3 个股指数据集上评价指标的详细结果。根据实验结果可以发现：相比于前文使用单一模型对时间序列进行预测，混合的模型使用有效提高了模型的预测表现，这与前人的研究结论一致；相比于未使用扩张卷积神经网络的对比方法而言，扩张卷积神经网络的使用的确有效提高了模型的预测表现；使用了注意力机制的模型较未使用注意力机制的模型拥有更高的预测精度，且提升效果较为明显，这表明虽然使用扩张卷积神经网络有利于提取多时间尺度的序列信息，但是其提取的信息有一定的冗余性，注意力机制的使用能让模型去除冗余信息和提取有效信息，从而提高模型的预测精度。

表4 DCNN_LSTM_AT与本文构造的基准模型在股指数据集上的表现Table 4 Performance of DCNN_LSTM_AT and benchmark model constructed in this paper on stock index datasets

4 结论

为了提高金融时间序列的预测精度，本文设计了一种新的时间序列预测模型DCNN_LSTM_AT。该模型先通过使用基于扩张卷积和LSTM 的编码器提取原始序列数据中不同尺度的有效信息，再通过使用带注意力机制的LSTM解码器有效利用提取的信息进行预测，从而达到提高模型的预测精度的目的，在多个股指数据集和个股数据集上的实验结果表明，该模型具有较好的预测精度和稳定性。由于本文模型的输入数据只考虑了历史数据中的开盘价、收盘价、交易量、交易金额、最高价、最低价等特征，而金融市场的表现实际上会受到很多因素的影响，故本文模型的性能还有进一步提升的空间。未来的工作将从这一方面入手，考虑将更多可能影响股票指数的影响因素如市场上股民的情绪、不同股市股指的表现，以及个股对应企业的财务指标等特征加入到模型的预测中，从而提高模型的精度。