多维联想，实现学生解题层次的提升——对一道几何题的探究与思考

王 伟

(浙江省宁波市象山县大目湾实验学校，浙江宁波，315700)

学生常说“不会的问题老师一讲就懂，但自己碰到就不知如何下手.”这反映出学生解题存在的一个普遍问题，即如何探寻解题思路.解题时，应当想些什么，怎么想.波利亚告诉我们：“你以前见过它吗？你是否知道与此有关的问题？你是否知道一个可能用得上的定理？”这说明解决问题离不开联想.教师如何引导学生发现问题所包含的有用信息，联想与之相关的内容，帮助学生解题？本文以一道中考改编题的解法探究为例，谈谈自己的实践与思考.

1 题目呈现

图1

2 解法探究

课程标准指出：“数学知识的教学需让学生体会对于某些数学知识可以从不同的角度加以分析、从不同的层次进行理解.”同时不同思维层次水平的学生思考问题的出发点不同，有的学生喜欢从已知条件入手，由因导果；有的学生喜欢从图形特征出发，从整体结构去寻找思路；也有学生习惯从结论出发，执果索因.观察本题，从已知条件来看有菱形、平行、线段倍长关系、角倍分关系，两条线段长，隐含条件是相似三角形；从图形特征来看有菱形、等腰三角形、隐含图形是平行四边形、全等三角形、相似三角形；从待求结论来看求的是菱形的边长即求线段长度的计算型问题.

2.1 转化已知条件，合理联想

解法1(截长+平行四边形+共边共角相似)

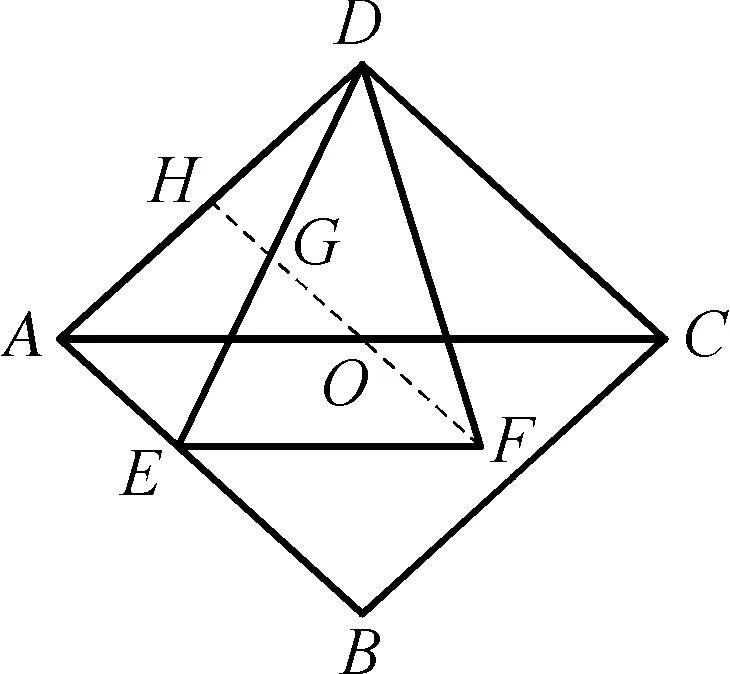
图2

如图2，在AC上截取AO=EF，连接FO并延长分别交DE，AD于点G，H.

∵EF∥AC，AO=EF.

∴四边形AEFO是平行四边形.

∴FH∥AB.

∵点O是AC中点.

∴点G，H分别是ED，AD的中点.

设CD=2t，则OH=t，GF=t+2-1=t+1.

∵FH∥AB.

又∵∠FEG=∠DEF.

∴△EFG∽△EDF.

解法2(补短+平行四边形+共边共角相似)

如图3延长EF，使EM=2EF，连接CM.

图3

∵AC∥EF，又∵AC=EM=2EF.

∴四边形AEMC是平行四边形.

∴AE=CM，∠EAC=∠M，∠EAC+∠ACM=180°.

∵∠EAC=∠ACD.

∴∠ACD+∠ACM=180°，即D，C，M三点共线.

∴△EFD∽△EDM.

解法3(平行四边形+共边共角相似+全等三角形)

如图4，连接BO交AC于点O，过点E画EF垂线与FO延长线交于点H，FH交DE于点G.同解法1可知，四边形AEFO是平行四边形，G是DE的中点.

图4

∴∠1=∠2=∠EDF，∠GEF=∠FED.

∴△GEF∽△FED.

∵EH⊥EF，DO⊥AC，EF∥AC.

∴EH∥DO.∴∠4=∠5而∠6=∠7.

∴△EGH≌△DGO.

∵∠2=∠1=∠3，EF=AO，∠HEF=∠DOA=90°.

∴△HEF≌△DOA.

2.2 应用图形特征，整体联想

任何一道数学问题都是有结构的，组成问题的各要素相互关联、相互制约，形成一个整体.从整体结构上去全面理解题意，可以寻得总体思路.菱形是图形的整体结构，联想到菱形的重要性质：中心对称.图形的中心对称也是用来解决与菱形以及平行四边形有关问题的重要方法.

解法4(中心对称+相似三角形)

图5

如图5，延长EF，使EM=2EF，连接CM，延长DF，交AB的延长线于点G.

同解法2得四边形AEMC是平行四边形.

∵AB∥CD.

∴∠M=∠GEF，∠MDF=∠G.

∴△MDF≌△EGF.

∴DF=FG=5，MD=EG.

∴△GEF∽△GDE.

解法5(中位线+全等三角形+共边共角相似)

如图6，连接CF并延长交AB于点N，延长DF，交AB的延长线于点M.

图6

∵EF∥AC，AC=2EF.

∴AE=EN=2，CF=FN.

∵AM∥CD.

∴∠M=∠MDC，∠MNF=

∠DCF.

∴△MNF≌△DCF.

∴DF=FM=5，MN=CD.

∴△MEF∽△MDE.

2.3 综合待求结论，合情联想

“结论也是已知信息”，由结论寻找条件，由条件推算结论，综合看条件与结论之间的联系是常用的解题手段.这是一道求线段长度的几何计算型试题.结合已知条件，联想到求线段的长度的常见的方法：勾股定理、相似三角形三边对应成比例.题中虽有菱形的对角线互相垂直这一性质可以构造直角三角形，但是不具备其他条件.题中存在相似三角形：△AEG∽△DGH∽△DEF∽△CGD，从中选取合适的相似三角形利用其对应边成比例建立方程求解.

解法6(AGE∽△DEF+△CDG∽△DFE+方程)

设AG=2x，GE=2y.

图7

∵EF∥AC.∴∠3=∠4.

∴△AGE∽△DEF.

∴DE=5x，EF=5y.

∴GD=5x-2y.

∵AC=2EF=10y.

∴CG=10y-2x.

∵∠EDF=∠2，∠5=∠3=∠4.

∴△CDG∽△DFE.

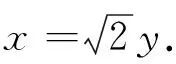
解法7(△AGE∽△DEF+△AGE∽△CGD+方程)

如图7，设AG=2x，GE=2y.

同解法6可得DE=5x，EF=5y，AC=2EF=10y.

∵∠1=∠2，∠3=∠5.

∴△AGE∽△CGD.

3 解后反思

3.1 多角度观察促进多维联想——发散思维

3.2 建立结构化的知识结构框图——关联思考

题目的信息开始是孤立的、零散的、杂乱的.首先经过思考，判定哪些是有用的，哪些是暂时用不着的，再考虑将有用的信息按怎样的先后顺序加以串联和组织，最后在头脑中形成解决问题的知识结构框图.如本题有序思考后解法2的知识结构框图如下图.

解法8解题关键是由已知条件AC=2EF，即F是EM的中点联想到构造平行四边形，解后再进一步思考该条件还可联想中线倍长得到解法4，还可联想中位线得到解法3，将这些解法整合在一起就形成本题解法的“关联性”结构链，促进学生解题思维的深层次发展.

数学教学的本质是“教会学生思考”，解题教学的重心需从传授现成的“数学结论”转向“数学思维”的培养.学生通过观察联想获得多种解法，经历了思维的发散，拓宽了思维的广度；通过有序思考形成解法的结构链，经历了思维的聚合，拓展了思维的深度，最终切实提高数学解题能力.