空间黏附足式爬行机器人的稳定性判据及蠕动步态
唐 玲,王克鹏,张 彬,魏世民
(北京邮电大学人工智能学院,北京 100083)
0 引 言
随着人类对太空探索、研究、开发和应用的能力不断提高与扩展,针对空间设备的建造、维护、维修、燃料加注以及轨道垃圾清理等在轨服务任务的需求也变得越来越迫切。空间环境复杂多变,为了降低风险和成本,减少航天员舱外作业,提高空间作业效率,空间机器人成为执行在轨服务任务的重要载体和辅助工具。其中,足式爬行机器人具有空间大范围行走与操作能力,但在空间微重力环境下没有重力锁和,黏附力成为机器人足端与航天器稳定接触的关键。工业中常使用的真空吸附、电磁吸附、湿黏附等接触方式均无法在空间中使用,而基于范德华力的干黏附材料适用于真空条件和多种材质的表面,因此,干黏附足式爬行机器人在空间应用方面得到了广泛关注。
2000年Autumn等发现壁虎能够在各种表面上稳定黏附是其脚掌上数百万根长度为30~130 μm的刚毛产生范德华力累积的结果。2014年,俄罗斯Barabanov等使用“Foton-M4”科学实验卫星搭载了5只壁虎进入外太空,验证了壁虎能够在失重环境下稳定黏附。因此,基于壁虎黏附机制发展的仿生干黏附材料和机构是微重力下实现固体间稳定黏附接触的最有效手段之一。
基于黏附机制,国内外不少团队、学者研发了各种黏附机构和机器人。2015年美国喷气推进实验室Hao等研制了手持式抓附机构,实现了在微重力环境下对目标物体的黏附抓取。同年,美国斯坦福大学的Bualat等为国际空间站中的Astrobee机器人设计了一款受壁虎启发的黏性抓手,采用微楔形粘合剂实现了在空间环境下的快速附着和分离。2021年李龙等提出了一种空间缓冲黏附机构,实现了黏附机构减小碰撞力且不发生回弹的效果。但黏附机构只是机器人的一部分,灵活度有限。在爬行机器人方面,2010年美国卡耐基梅隆大学的Unve和Seo等研发了履带式爬壁机器人Tank Bot,用聚二甲基硅氧烷(PDMS) 为黏附材料,实现了在竖直壁墙面上爬行。南京航空航天大学的李宏凯等使用复合聚合聚乙烯醇(PVS)按照蘑菇状柱阵列制作仿生干胶材料,并将其应用于履带轮式爬壁机器人,可以在竖直表面进行稳定附着和移动。但是黏附爬行的履带机器人具有转弯困难,转弯过程黏附力迅速下降的缺点。2020年韩国岭南大学Liu等使用带有弹性体的干黏附系统研发了一款连杆式爬壁机器人,机器人使用了一种连接内外车架的并联四连杆机构,通过连杆单一旋转实现机器人的行走运动,但机器人灵活性受限,仅适用于无障碍的平面。2021年Bian等设计了一款可折叠的六足攀爬机器人,能够在不同粗糙度和形状的表面进行稳定攀爬,但是该机器人需要机器人重力与攀爬爪的勾爪锁合,难以适用于无重力的空间环境。此外,六足机器人对于机器人的爬行运动自由度过于冗余,而四足机器人具有与六足机器人相同的运动灵活性,但机械系统简单,重量上具有较大的优势。
近年来国内外四足机器人发展迅速,一系列四足仿生机器人被开发出来,如麻省理工学院的Cheetah 3机器人、Boston Dynamic的Dog系列机器人、宇树科技的Laikago四足机器人等。四足机器人步态规划研究主要着力于步态最优适应性和深度强化学习控制两个方面。2018年McClain等提出了一个由能量项和稳定性项的成本函数,通过对其评估来确定四足机器人在存在预期干扰的情况下行走的最佳静态稳定步态。2021年Saraf等在波士顿动力的Webots模拟器上使用模型预测控制器(MPC)实现了四足机器人步态规划的自动校正。同济大学的刘成菊等于2021年提出了一套在线调制和融合多传感器信息的仿人机器人自适应行走控制,搭建自学习CPG模型,提高了四足机器人行走步态的适应性。2020年Tsounis等使用动态可行性标准制定马尔科夫决策过程,使用本体感知和外部传感信息进行策略制定,使得四足机器人能够在窄桥、间隙和碎石等环境下稳定运动。2021年燕山大学吴晓光等利用一种Ape-X DPG算法学习双足机器人步态,实现了四足机器人较大斜坡范围内的稳定行走。但空间和地面环境力学环境差别较大,地面与空间环境下,四足式机器人的稳定性原理与完全不同,因此,以上地面四足机器人的控制策略无法适用于空间零重力环境。2020年哈尔滨工业大学的游斌弟等设计了应用于空间细胞机器人的攀爬步态,用于解决面向空间桁架的攀爬维修问题,但机器人操控复杂,足端与目标为刚性连接,不适用于黏附爬行机器人。
本文针对空间在轨服务任务中黏附足式爬行机器人应用需求和现有研究的不足,提出一种通过足端和腹部黏附实现爬行的机器人构型,分析空间机器人黏附爬行的稳定性原理,推导一种空间环境下黏附足式爬行机器人行走的稳定性判据,使用该判据,分析空间黏附足式爬行机器人3+1步态的不稳定性,并规划适用于空间微重力环境的稳定爬行的蠕动步态。最后,通过仿真验证空间黏附足式爬行机器人稳定性理论及蠕动步态的有效性。
1 黏附足式爬行机器人构型设计
面向空间微重力环境下足式爬行机器人稳定行走应用需求,在传统足式机器人构型的基础上,提出了一种新式黏附足式爬行机器人构型,机器人由本体、四条腿、腿部足和腹部足组成,腿在本体两侧对称分布,机器人整体结构如图1所示,其中表示左前腿部足,表示左后腿部足,表示右前腿部足,表示右后腿部足,表示腹部足。
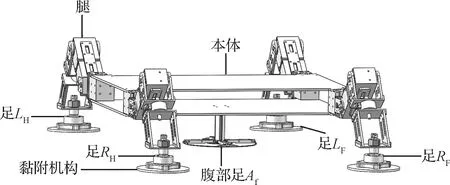
图1 黏附足式爬行机器人整体结构Fig.1 Overall structure of the adhesive-feet crawling robot
机器人每条腿的结构相同,为串联结构,包含3个转动关节,腿部与足部的连接为三自由度的被动球铰。腿部足和腹部足底部安装有仿干黏性吸附材料,可黏附在空间表面行走。
机器人简化结构如图2所示,机器人本体坐标系原点位于机器人身体上板几何中心,轴正方向指向身体长边,轴正方向指向身体短边,轴方向为机器人的前进方向,为机器人躯干宽度,为躯干长度,为躯干高度,,,依次为腿部臂1、臂 2和臂3的长度。
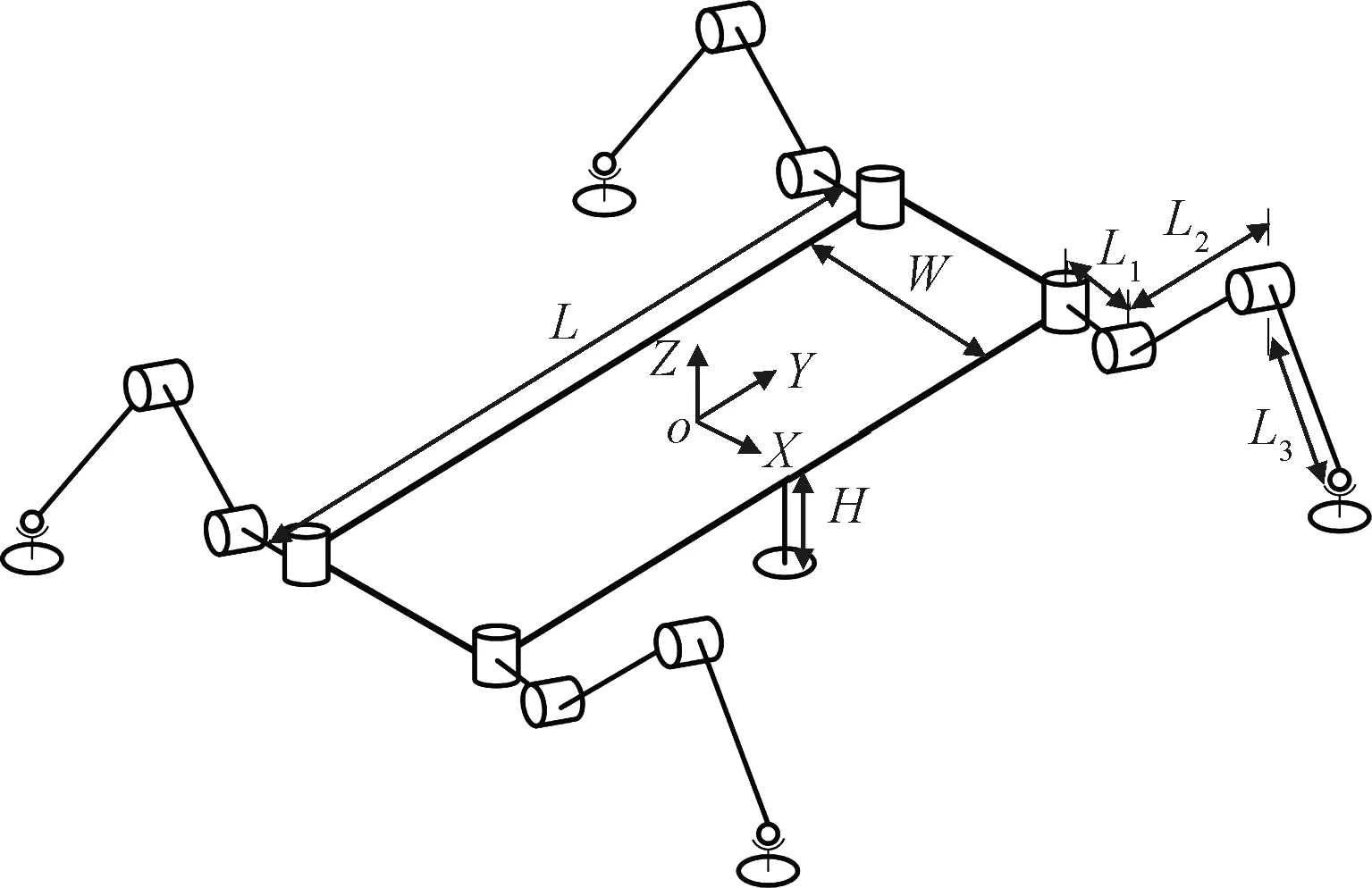
图2 黏附足式机器人简化结构Fig.2 Simplified structure of the adhesive-feet crawling robot
机器人结构参数如表1所示。
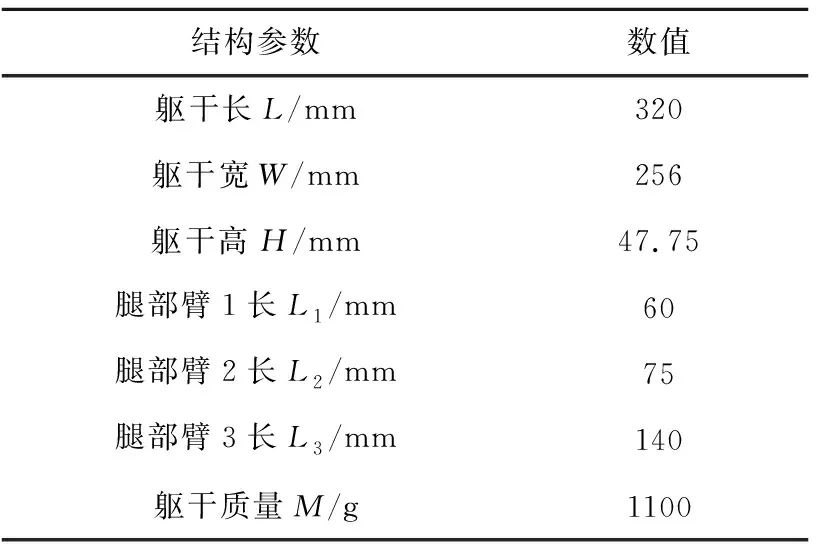
表1 机器人结构参数Table 1 Structural parameters of the robot
2 空间黏附足式爬行机器人稳定性判据
在空间微重力环境下,黏附足式爬行机器人主要受到足端黏附力和脱附力的作用。在机器人行走过程中,若足端与地面有接触,则称该足为支撑足,若足端与地面无接触,则称该足为摆动足。
本文提出一种面向空间黏附足式爬行机器人的稳定性判据,其基本思想为:在机器人行走过程中,对其四条腿的足端向地面进行投影,若对角支撑足沿支撑对角线的黏附力矩大于摆动足沿支撑对角线的脱附力矩,则机器人处于稳定状态,反之则会发生倾倒。
以左前足抬起为例,上述判据的原理如图3所示,图中空心圆点表示足为摆动状态,实心圆点表示足,和为支撑状态,其中支撑足与的连线称为支撑对角线,支撑足与摆动足在支撑对角线的两侧。
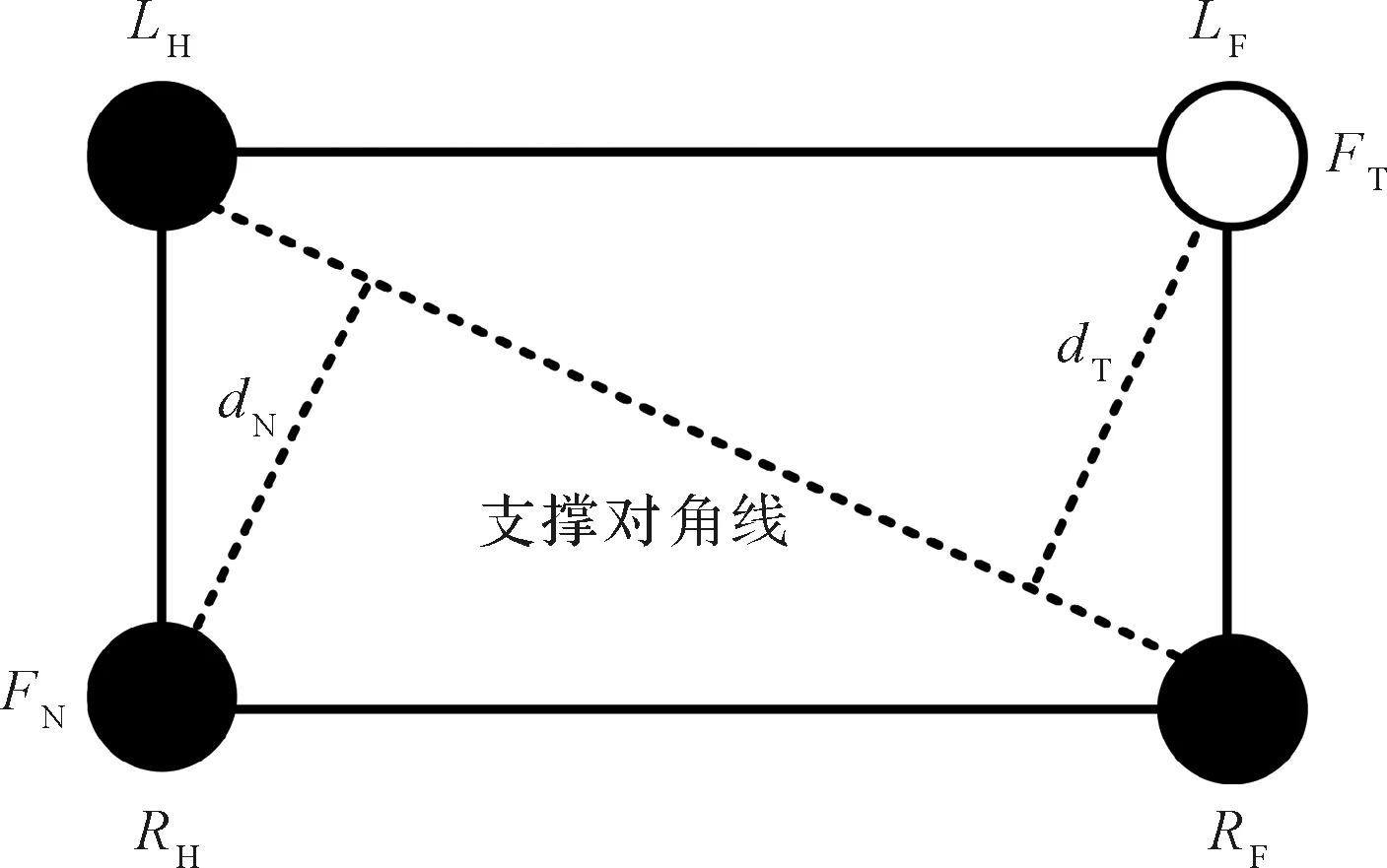
图3 机器人稳定性判定原理Fig.3 Stability determination principle of the robot
为摆动足的最大脱附力,为摆动足到支撑对角线的投影距离,为支撑足的最大黏附力,为支撑足到支撑对角线的投影距离。
定义稳定裕度值:
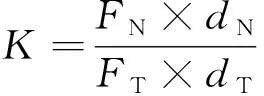
(1)
由于机器人足端采用相同的黏附装置,因此,当机器人迈腿时,=,式(1)简化为:
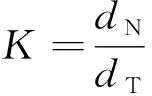
(2)
若黏附足式爬行机器人处于平衡状态,则值为正且大于1,且值越大,四足黏附足式爬行机器人的稳定性越好。当小于1时,机器人为不稳定状态。
3 机器人稳定性分析及步态规划
基于上述稳定性判定方法,分析黏附足式爬行机器人3+1步态的不稳定性,并规划适用于空间微重力环境的蠕动稳定步态。
3.1 3+1步态规划及步态稳定性分析
黏附足式爬行机器人的3+1步态要求任意时刻至少有三条腿支撑地面,因此每次只能抬起一条腿,共有6种迈腿顺序:1234、1243、1324、1342、1423和1432,如图4所示,其中1表示左前足,2表示右前足,3表示左后足,4表示右后足。
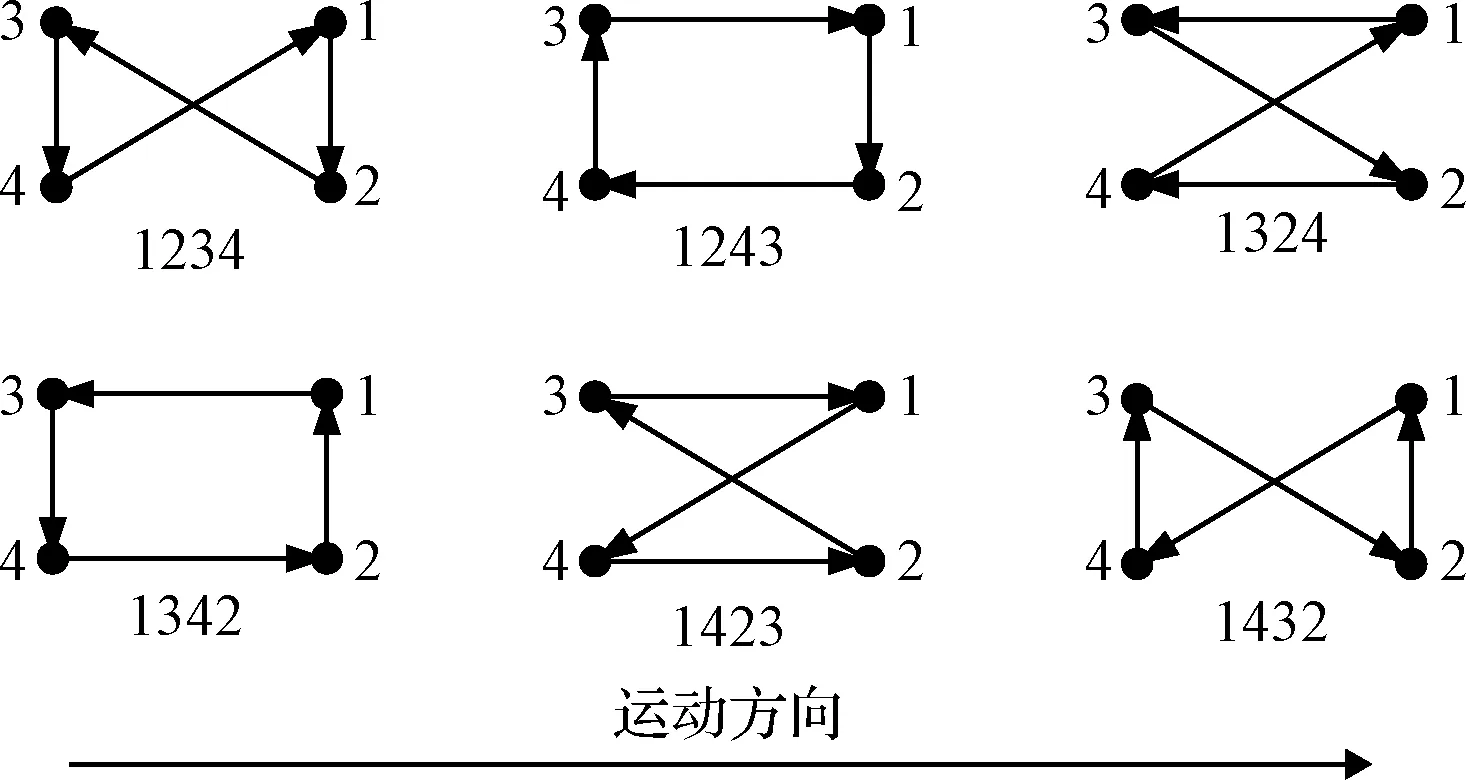
图4 3+1步态6种迈腿顺序Fig.4 6 steps in the 3+1 gait
当机器人步距为时,以1234迈腿顺序为例,四足机器人3+1步态的稳定裕度值变化如图5所示。
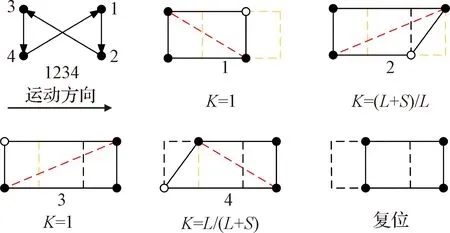
图5 3+1步态稳定裕度K值Fig.5 Stability margin K in the 3+1 gait
3+1步态6种迈腿顺序的最大稳定裕度值如表2所示:

表2 3+1步态最大稳定裕度K值Table 2 Maximum stability margin K in the 3+1 gait
由表可知,不管采用何种3+1步态,机器人稳定裕度值均会出现小于1的情况,不满足空间微重力环境下黏附足式爬行机器人行走稳定性要求,因此,3+1步态并不适应于黏附足式爬行机器人空间行走。
3.2 蠕动步态规划及步态稳定性分析
本文规划了一种适用于空间微重力环境的黏附足式爬行机器人蠕动步态,运动简图如图6所示,当机器人迈腿时,支撑足端与地面保持贴合,在完成四条腿依次摆动后将本体抬起向前移动。
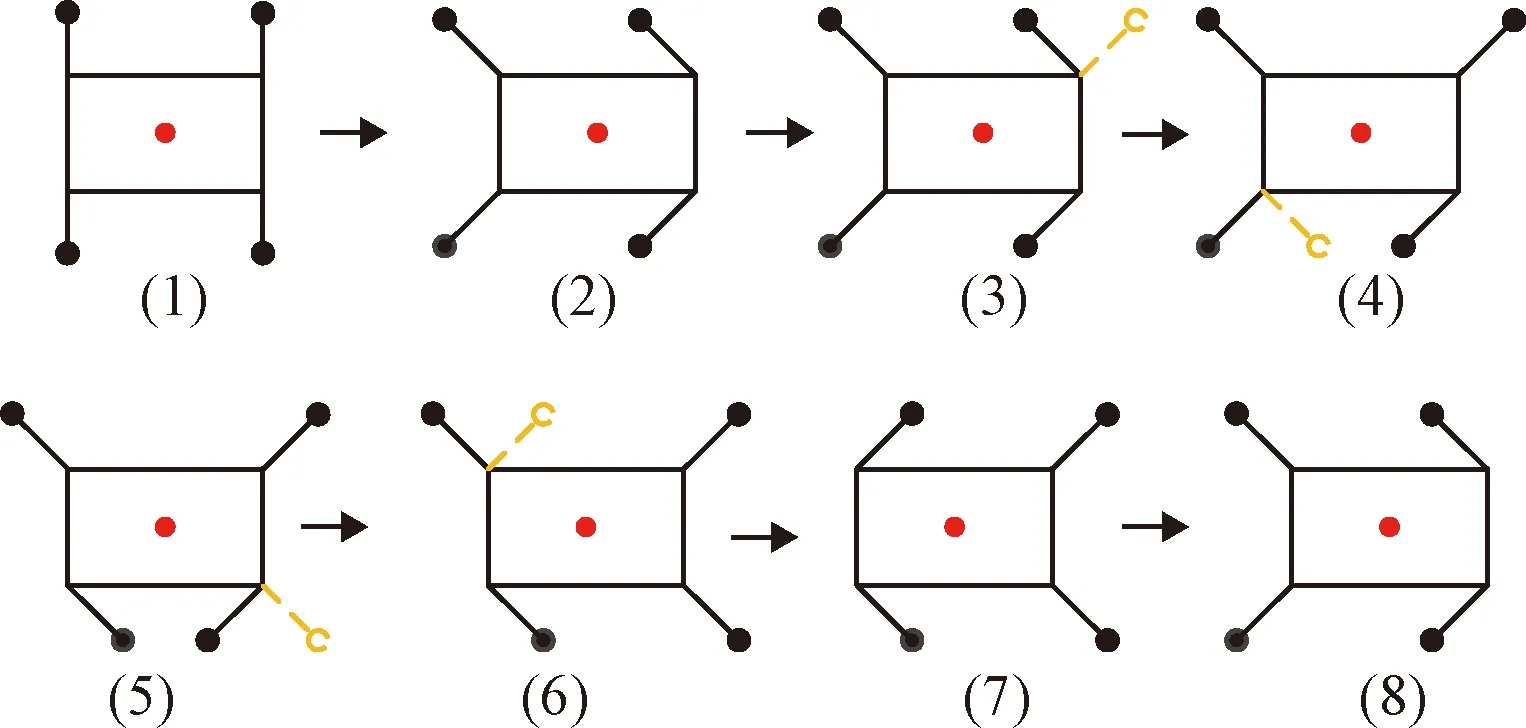
图6 蠕动步态运动简图Fig.6 Schematic diagram of the creep gait movement
当腿部足端处于支撑相时,足端与地面接触点用实心圆点表示,当腿部足端处于摆动相时,落地足端则用空心圆圈表示,红色圆点为机体质心,蠕动步态对应的机器人状态描述如下:
(1)起始状态,四条腿对称分布在机体两侧,====0;
(2)本体在四条腿的支撑下向前移动半个步距,Δ=/2,到达一个周期内的起始状态;
(3)完成一次抬放动作,跨距,耗时0.2;
(4)完成一次抬放动作,跨距,耗时0.2;
(5)完成一次抬放动作,跨距,耗时0.2;
(6)完成一次抬放动作,跨距,耗时0.2;
(7)本体在四条腿的支撑下向前移动一个步距,Δ=,耗时0.2;
(8)回到一个周期内的起始状态,至此,一个步态周期内所有机械腿和足端运动规划结束。
其中,表示机器人步态的一个周期时间。蠕动步态的时序图如图7所示,当腿部足端为支撑相时,用黑色块表示,摆动相为空白表示。
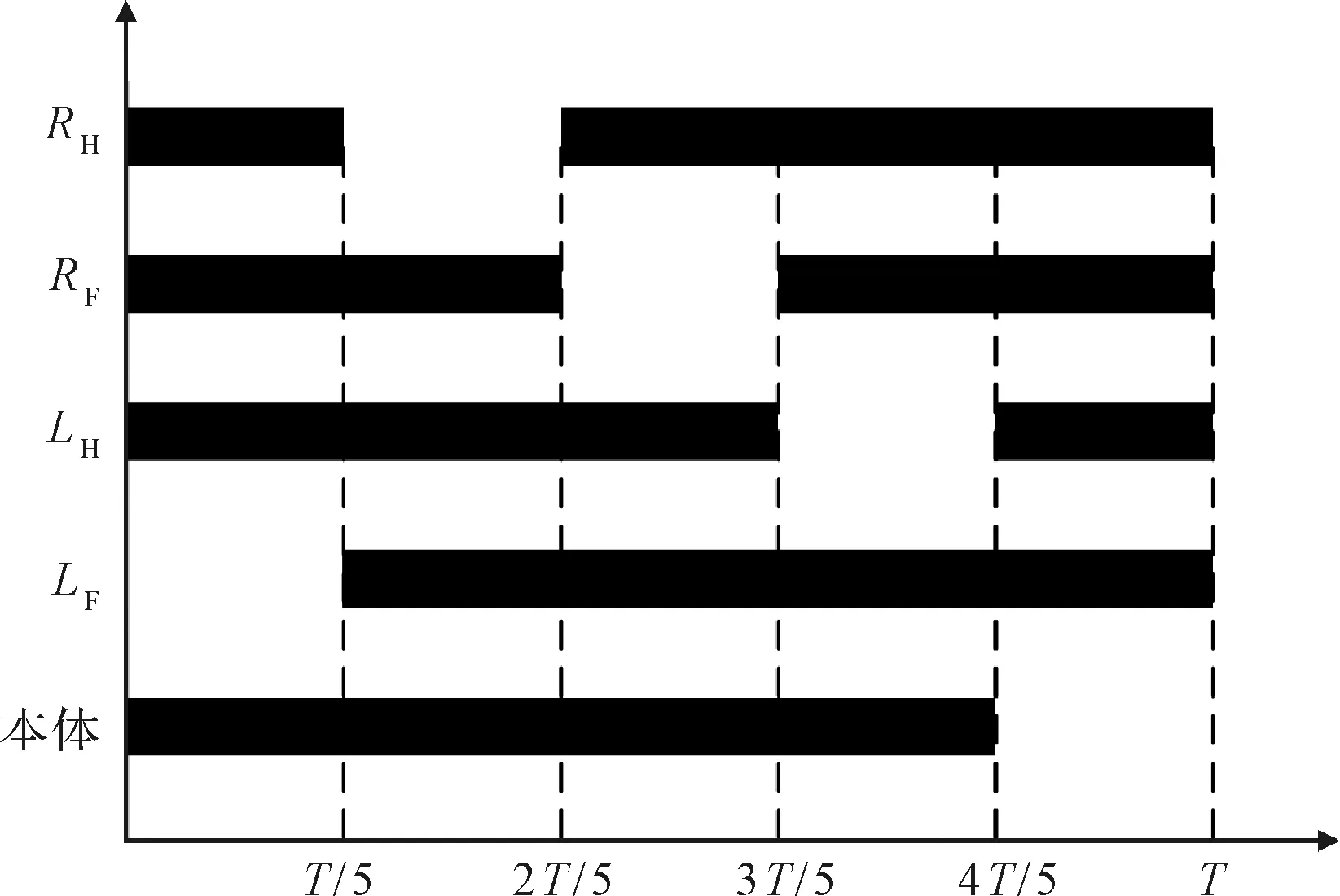
图7 蠕动步态时序图Fig.7 Time sequence diagram of the creep gait
为了计算出机器人的稳定裕度值变化情况,先画出四足机器人运动关键点坐标图,如图8所示:
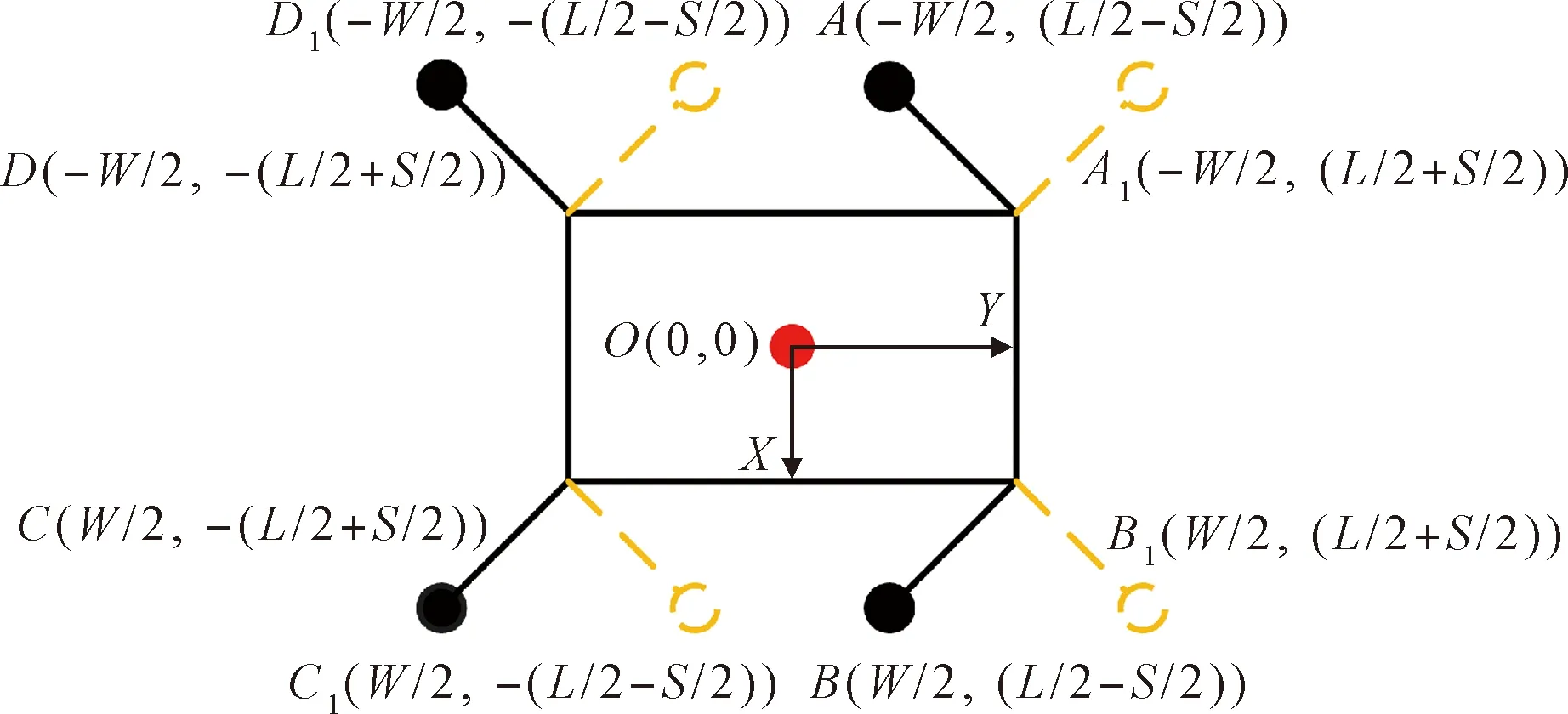
图8 机器人关键点坐标Fig.8 Coordinates of robot key points
设本体质心位置为坐标系原点,前进方向为坐标,则关键点坐标为:
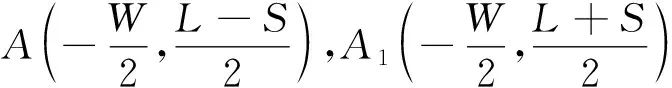
(3)
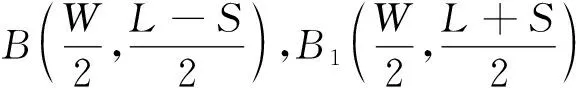
(4)
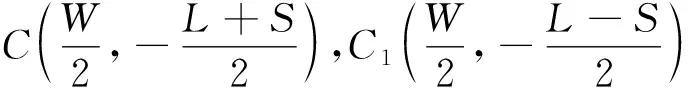
(5)
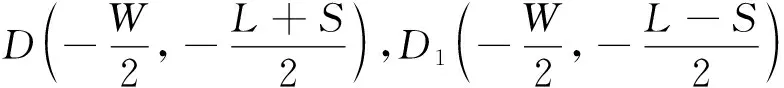
(6)
1)当摆动足为左前足时:
(1)假设支撑对角线为:
摆动足为,支撑对角线为时,机器人各足端位置几何关系如图9所示。
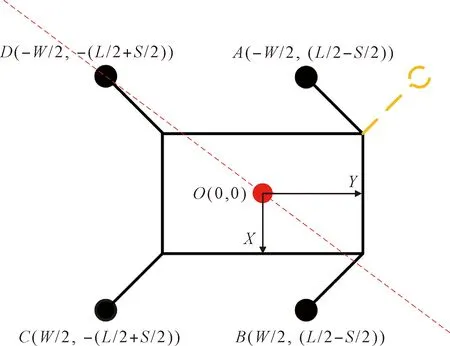
图9 支撑对角线为OD时足端几何关系示意图Fig.9 The geometric relation diagram of the feet when the supporting diagonal is OD
点到直线的距离:
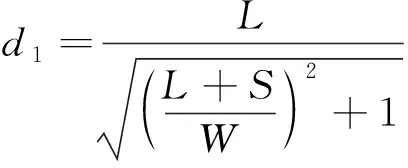
(7)
点到直线的距离:
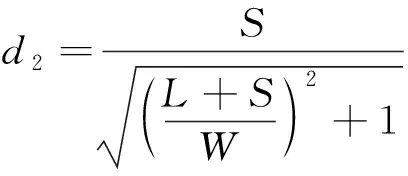
(8)
点到直线的距离:
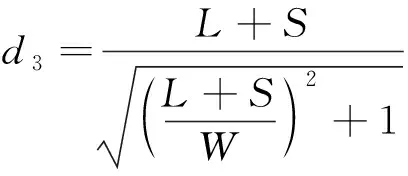
(9)
稳定裕度值:
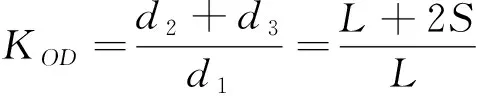
(10)
(2)假设支撑对角线为
点到直线的距离:
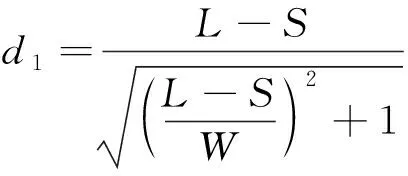
(11)
点到直线的距离:
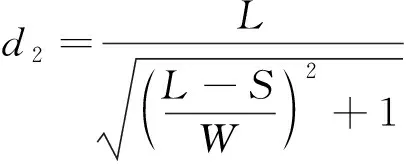
(12)
点到直线的距离:
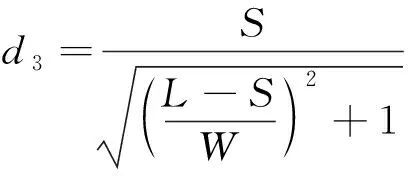
(13)
稳定裕度值:
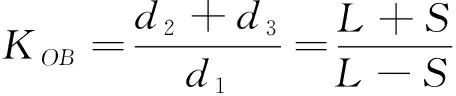
(14)
由于:
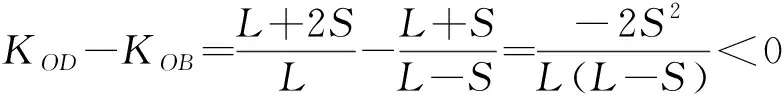
(15)
所以:
<
(16)
取较小值:
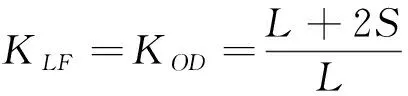
(17)
2)当摆动足为右后足R时,支撑对角线为
点到直线的距离:
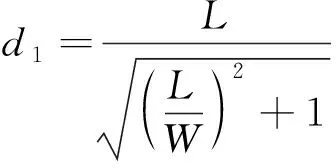
(18)
点到直线的距离:
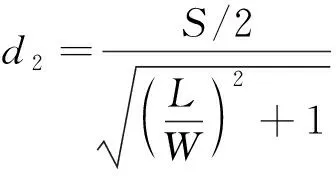
(19)
点到直线的距离:
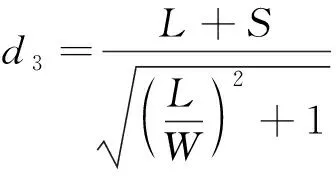
(20)
稳定裕度值:
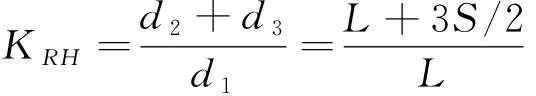
(21)
3)当摆动足为右前足时,支撑对角线为
点到直线的距离:
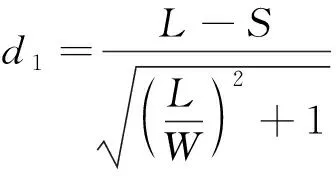
(22)
点到直线的距离:
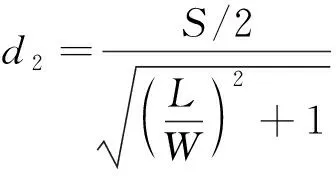
(23)
点到直线的距离:
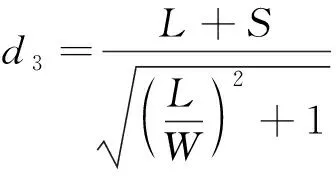
(24)
稳定裕度值:
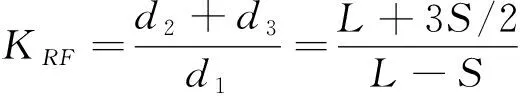
(25)
4)当摆动足为左后足时:
(1)假设支撑对角线为:
摆动足为,支撑对角线为时,机器人各足端位置几何关系如图10所示。
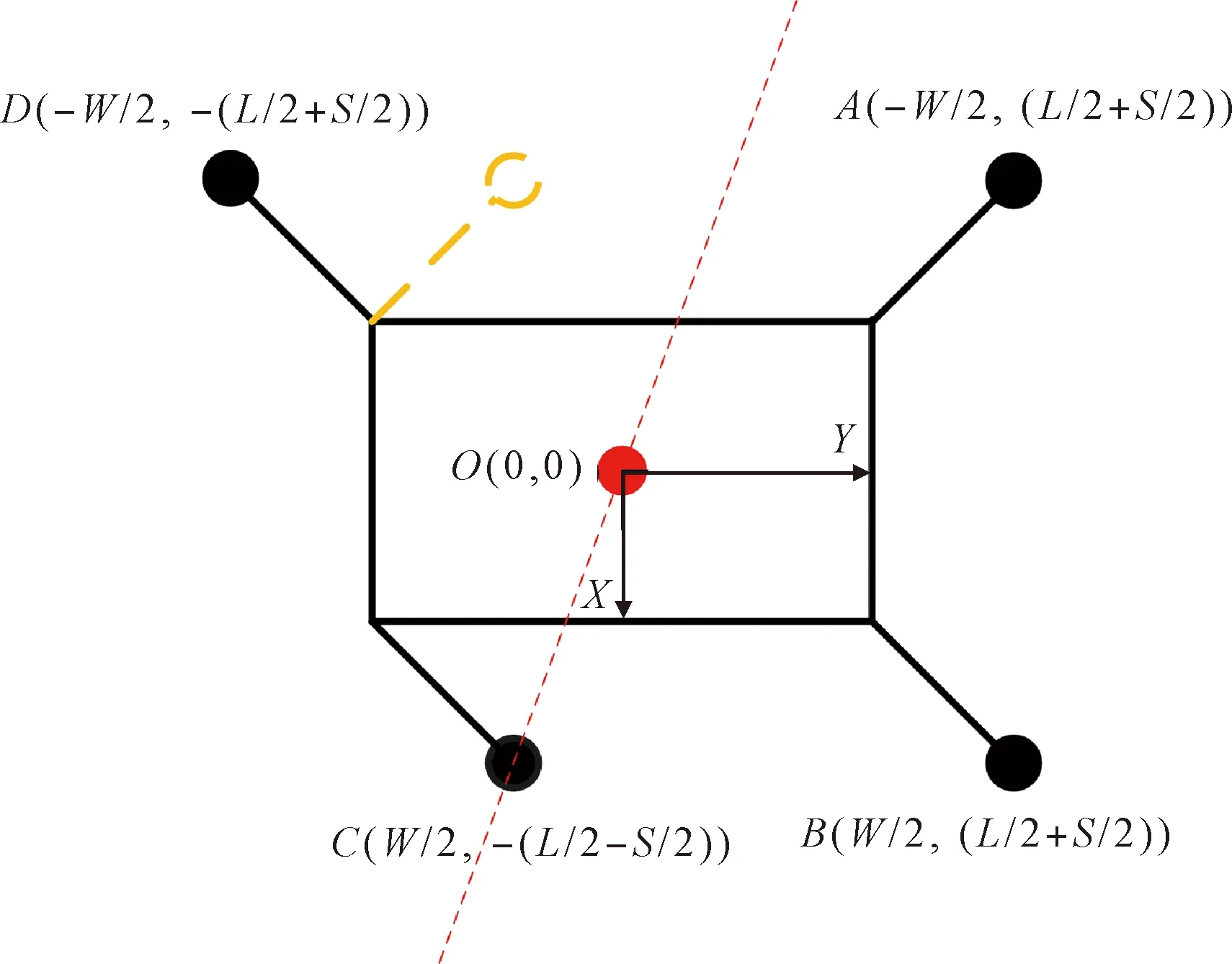
图10 支撑对角线为OC时足端位置几何关系示意图Fig.10 The geometric relation diagram of the feet when the supporting diagonal is OC
点到直线的距离:
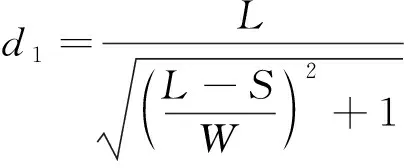
(26)
点到直线的距离:
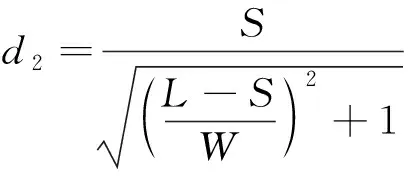
(27)
点到直线的距离:
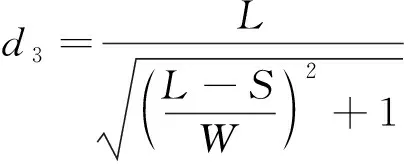
(28)
稳定裕度值:
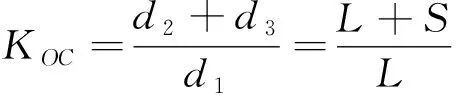
(29)
(2)假设支撑对角线为
点到直线的距离:
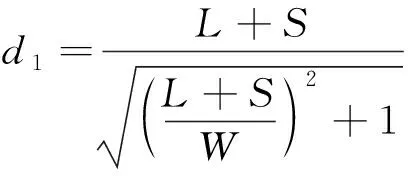
(30)
点到直线的距离:
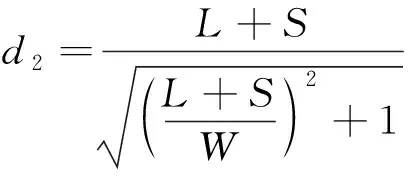
(31)
点到直线的距离:
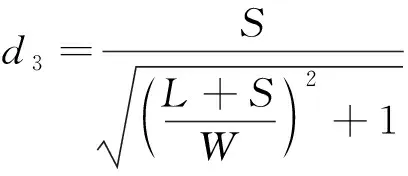
(32)
稳定裕度值:
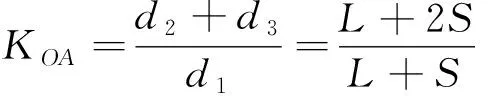
(33)
由于:
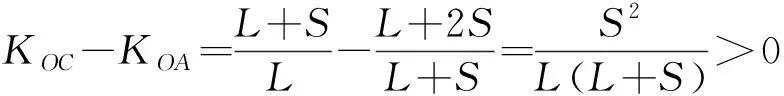
(34)
所以:
<
(35)
取较小值:
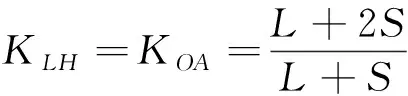
(36)
在一个蠕动步态周期内,左前足、右后足、右前足、左后足的稳定裕度值变化如表3所示:

表3 动步态稳定裕度K值Table 3 K value of peristaltic gait stability margin
由表可知,黏附足式爬行机器人采用蠕动步态时,稳定裕度值与和有关,与无关,且当一定时,越大,值越大。当取最大值时,=32;当=1时,=0;只要0<<,均满足稳定裕度要求,因此,蠕动步态满足空间稳定性要求。
4 动力学仿真分析
为了验证机器人稳定性理论以及蠕动步态规划的合理性,分别对3+1步态和蠕动步态进行动力学仿真,分析两种步态的稳定性能。
4.1 机器人仿真模型
在ADAMS中建立机器人虚拟样机模型,重力加速度设置为0 m/s,机器人足底、腹部与平面接触参数设置相同,如表4所示。

表4 接触力属性Table 4 Properties of the contact force
机器人黏附力采用如图11所示的黏附力与距离曲线关系模型,关系式为:
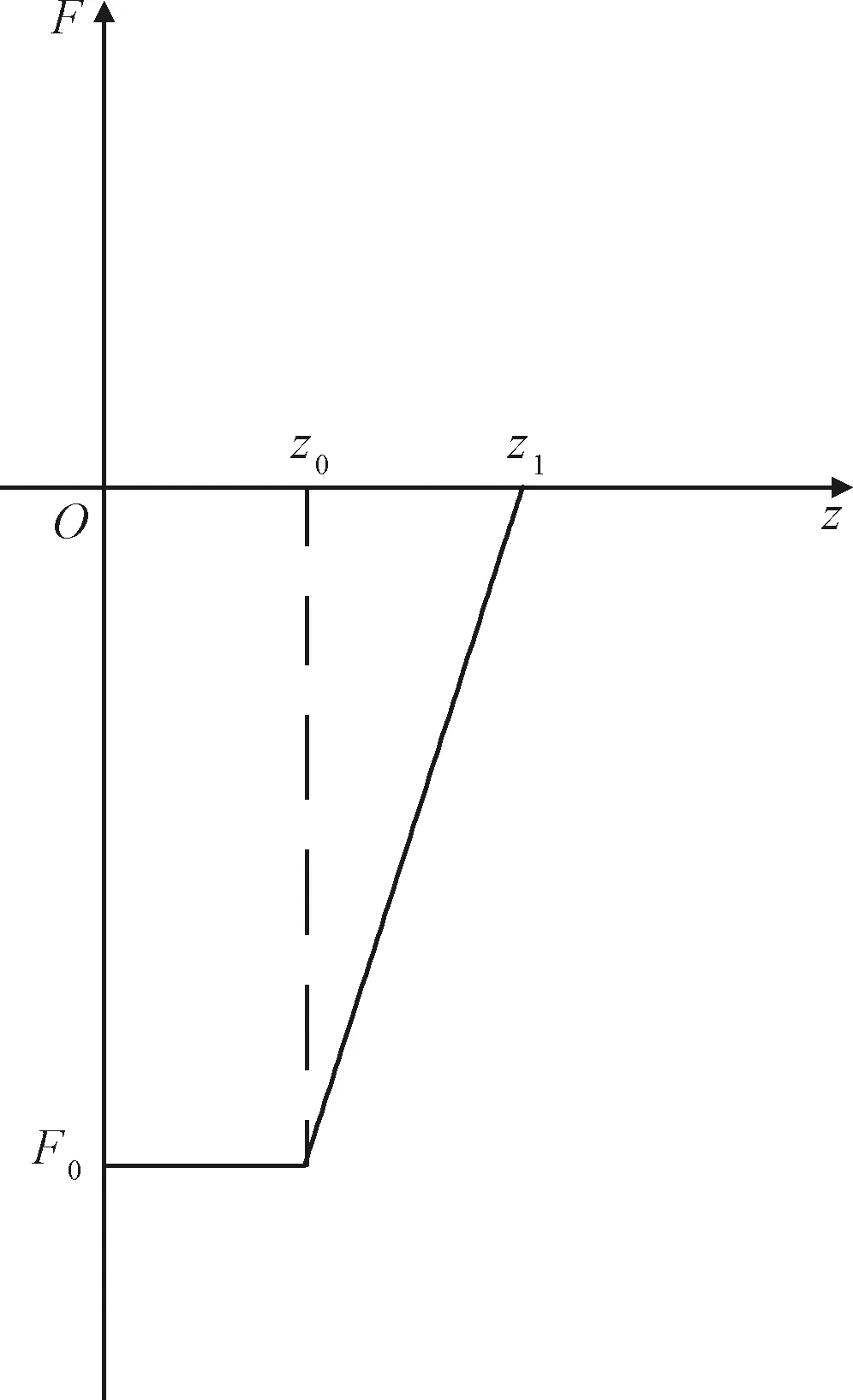
图11 机器人黏附力大小Fig.11 Adhesion force of the robot
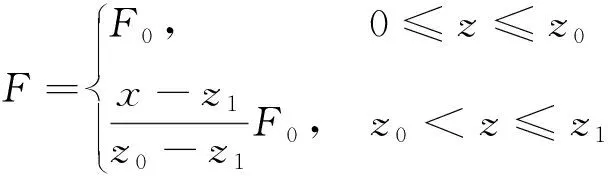
(37)
式中:为黏附力大小,为足底与接触面的距离。该曲线模拟了机器人足端和腹部机构黏附和脱附的作用力变化过程,在仿真中=-10 N,=2 mm,=4 mm。
机器人足端的运动轨迹规划如图12所示,图中为抬腿高度,为跨步距离。迈腿时先将足端沿垂直于接触面的方向抬起,然后与接触面保持一定距离向前移动,最后沿垂直于接触面的方向落下。在仿真中=20 mm,=60 mm。
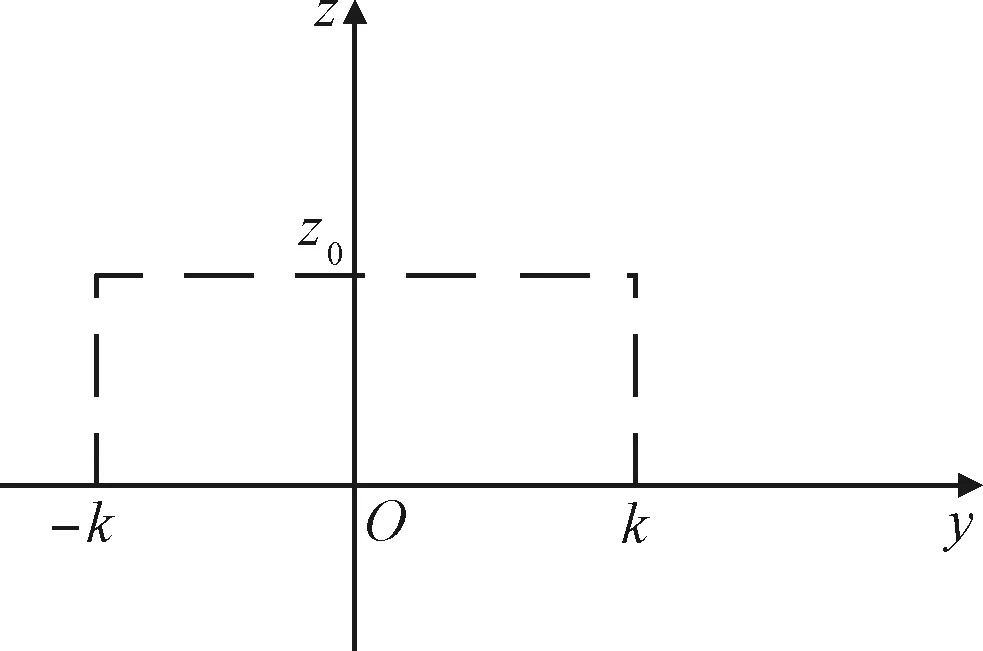
图12 足端运动轨迹Fig.12 Foot movement track
在ADAMS/view仿真环境下,黏附足式爬行机器人首先由零位构型运动至初始构型,之后完成1个周期(40 s)的黏附爬行运动,仿真步长设置为0.01 s,仿真时间为48 s。
4.2 蠕动步态仿真分析
仿真动画视图
蠕动步态仿真动画视图如图13所示,从图中可以看出,机器人以所规划的蠕动步态稳定行走。
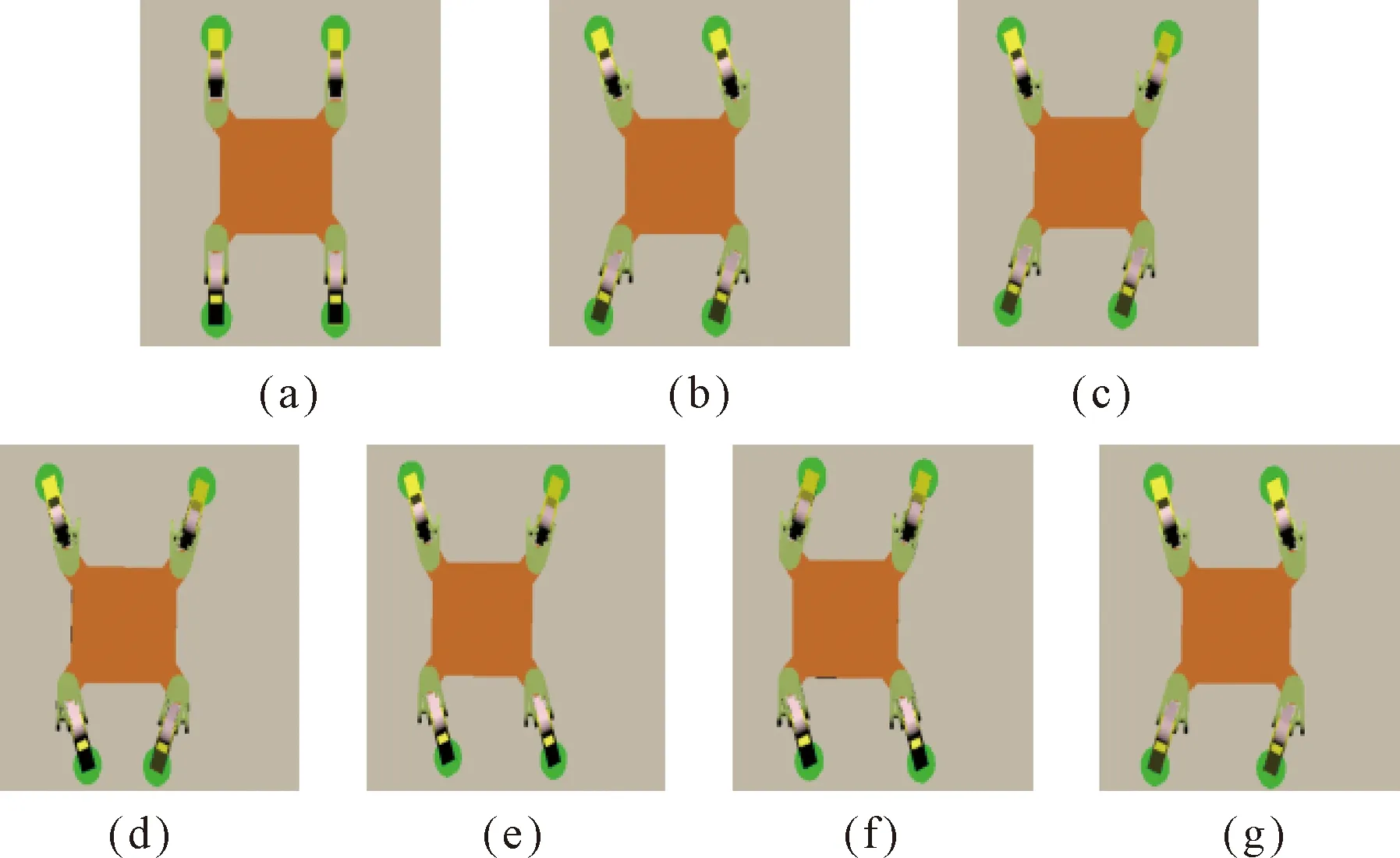
图13 蠕动步态仿真动画Fig.13 Creep gait simulation animation
本体质心位移
蠕动步态本体质心在,,方向上的位移曲线如图14所示,图中表示位移,表示时间,三条曲线依图例顺序为轴、轴和轴方向上的质心位移。
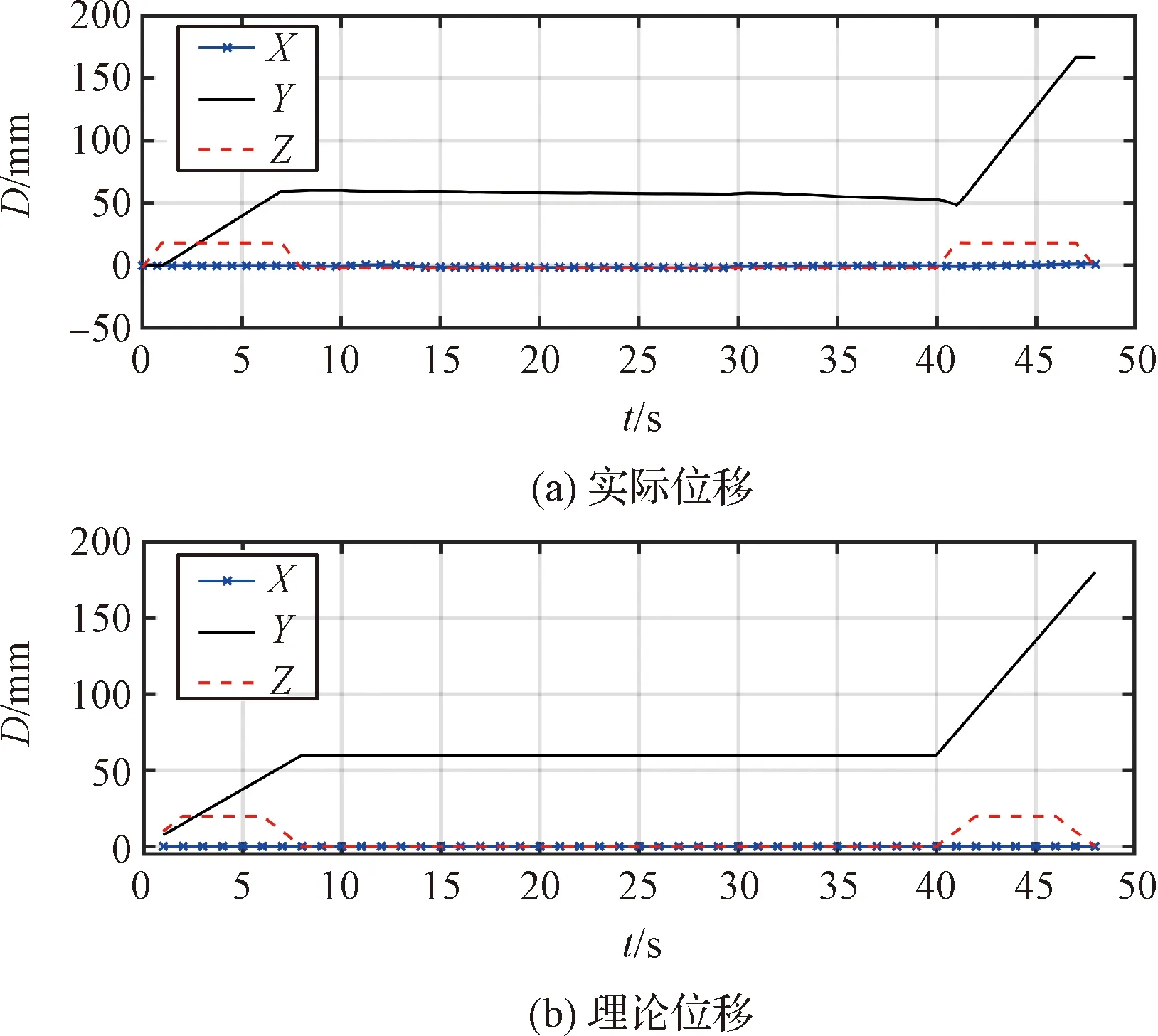
图14 蠕动步态本体质心位移Fig.14 Center of mass shift of the body in the creep gait
从图14中可以看出,机器人质心在方向上的实际位移与理论位移相比最大偏差仅为1.3 mm,方向上最大偏差为3 mm,方向上为0.7 mm,说明机器人能够在所设计的蠕动步态下沿着预定的方向平稳地运动,质心运动偏差较小,未出现黏附足式爬行机器人静步态常见的质心间歇不平稳运动。
足端抬起位移
蠕动步态机器人足端在方向抬起的位移曲线如图15所示,图中表示位移,表示时间,四条曲线依图例顺序为左前足、左后足、右前足和右后足在方向上的足端位移。
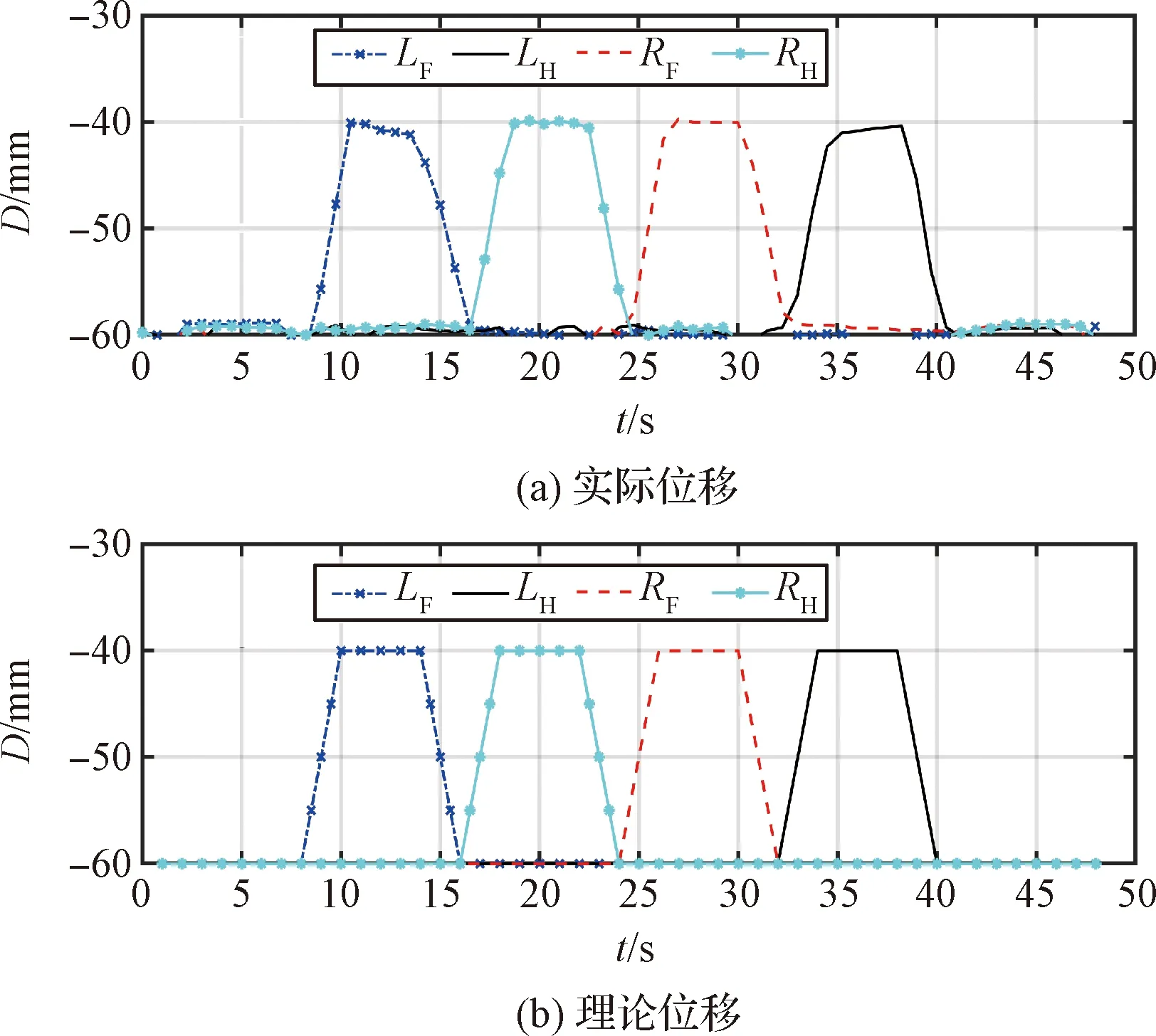
图15 蠕动步态足端抬起位移Fig.15 Foot lifting displacement in the creep gait
从图15中可以看出,各个足端的抬起位移基本无偏差,左前足和左后足在方向的位移最大偏差为1 mm,右后足和右前足最大偏差为0.2 mm,说明机器人腿部运动符合预期设计。
4.3 3+1步态仿真分析
仿真动画视图
3+1步态仿真动画视图如图16所示,从图中可以看出,机器人未能以本文所规划的3+1步态稳定行走,行走过程发生较大偏航。此外在动画中可以观察到机器人爬行过程中震动较剧烈。
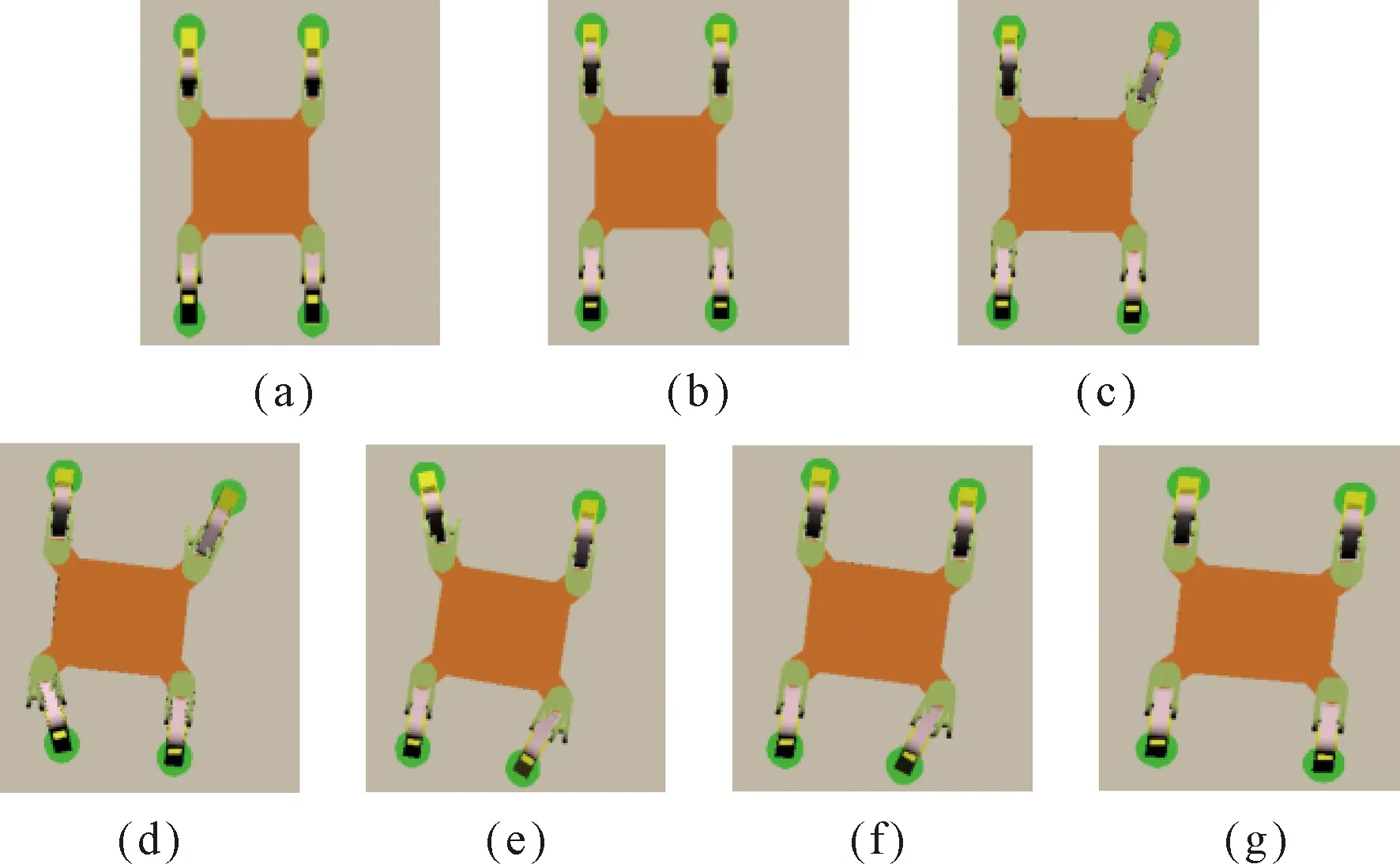
图16 3+1步态仿真动画Fig.16 3+1 gait simulation animation
本体质心位移
3+1步态本体质心在,,方向上的位移曲线如图17所示,图中表示位移,表示时间,三条曲线依图例顺序为轴、轴和轴方向上的质心位移。
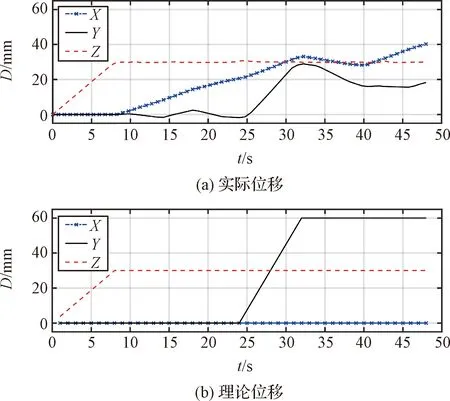
图17 3+1步态本体质心位移Fig.17 Center of mass shift of the body in 3+1 gait
从图中可以看出,机器人质心在方向上的实际位移与理论位移相比偏差最大值为37.5 mm,方向上位移偏差最大值为45 mm,方向上为2 mm,运动结束时偏航角为16.5 °,说明机器人未能在所设计的3+1步态下沿着预定的方向平稳地运动,质心运动偏差极大,出现严重的质心间歇不平稳运动。
足端抬起轨迹
3+1步态机器人足端在轴方向抬起的位移曲线如图18所示,图中表示位移,表示时间,四条曲线依图例顺序为左前足、左后足、右前足和右后足在方向上的足端位移。

图18 3+1步态足端抬起位移Fig.18 Foot lifting displacement in 3+1 gait
从图中可以看出,各个腿的足端位移均发生较大偏差,在方向上,左前足的位移最大偏差为7.5 mm,右后足为6.4 mm,左后足为11 mm,右前足为5 mm,与规划数据差别较大。
4.4 两种步态稳定性比较
蠕动步态与3+1步态行走过程质心稳定性参数对比结果如表5所示:
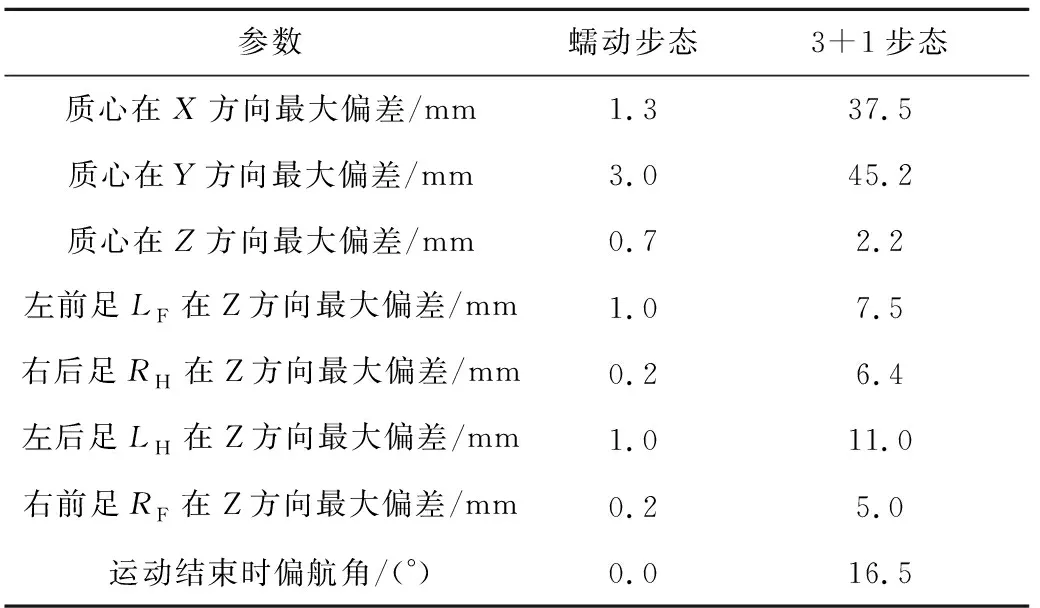
表5 两种步态关键参数对比Table 5 Key parameters comparison of the two gaits
由表可知,3+1步态质心位移偏差和各个足端的偏差均远大于蠕动步态,3+1步态偏航角为16.5°,而蠕动步态无偏航。因此得出:黏附足式爬行机器人蠕动步态各项稳定性指标均优于3+1步态,可以实现空间微重力环境下稳定行走,而3+1步态并不适用于空间行走。
5 结 论
本文提出了一种通过足端和腹部黏附实现爬行的机器人构型,研究了空间机器人黏附爬行的稳定性原理,推导了一种空间环境下黏附足式爬行机器人行走的稳定性判据,规划适用于空间微重力环境的稳定爬行的蠕动步态,并对其进行仿真验证,得出以下结论:
1)根据推导的空间黏附足式爬行机器人稳定性判据得出:空间黏附足式爬行机器人3+1步态的稳定裕度值均会出现小于1的情况,不满足机器人行走稳定性要求;蠕动步态的稳定裕度值与和有关,与无关,当0<<,即可满足机器人行走稳定性要求。
2)通过仿真得出:机器人采用常规的3+1步态,行走过程中误差较大,机器人爬行60 mm,机器人质心X运动偏差为45 mm,足端运动偏差为11 mm,偏航角度16.5 °。因此,黏附足式爬行机器人在空间环境中,常规的3+1步态不符合稳定性要求,与理论推导结果一致。
3)通过仿真得出:机器人采用蠕动步态爬行150 mm,运动过程中机器人质心运动偏差小于3 mm,足端位移偏差小于1 mm,偏航角度为0.0°。结果表明基于所设计的改进机器人构型依靠其足底和腹部黏附,机器人使用蠕动步态爬行稳定性较高,验证了机器人结构改进设计和蠕动步态的合理性,与理论推导结果一致,满足空间稳定行走要求。
本文提出的空间黏附足式爬行机器人的稳定性判据及蠕动步态,对未来黏附足式爬行机器人在轨服务的应用具有一定的参考意义。

