高超声速机动目标天基跟踪鲁棒性滤波方法

魏世君，翟 光，孙一勇，毕幸子，汪宏昇

(1. 北京理工大学宇航学院，北京 100081；2. 中国科学院微小卫星创新研究院，上海 201203；3. 中国运载火箭技术研究院研究发展部，北京 100076)

0 引 言

高超声速滑翔飞行器(Hypersonic glide vehicle, HGV)可在临近空间内实现5倍以上声速的机动突防飞行。为了实现对HGV的有效拦截，需首先完成对HGV飞行轨迹的准确跟踪。受地球曲率、大气散射等因素影响，地基雷达难以对HGV进行持续稳定的探测跟踪。由于HGV飞行过程中红外特性显著，天基红外传感器在未来将成为HGV的有效探测手段。然而，HGV在高速飞行过程中不断实施轨迹机动，由于机动幅值及起始时间等信息未知，采用传统卡尔曼滤波等方法进行轨迹估计跟踪时，极易导致滤波误差发散并丢失目标。因此仍需基于天基红外探测信息，设计针对目标未知机动的鲁棒性滤波跟踪算法，实现对目标飞行状态的准确估计。

当前，针对HGV轨迹跟踪问题，大部分研究工作采用的方法为强跟踪、扩维卡尔曼滤波以及交互多模型滤波。文献[10]采用多模型交互滤波，对Singer,CA,CT等运动学模型的跟踪结果进行融合；文献[11]在Singer模型和扩维卡尔曼滤波的基础上，基于多个具有不同时间常数的子滤波器构建交互多模型滤波器，以适应目标的不同机动频率；文献[12-14]根据气动特性和制导律推导了机动模型的参数取值，适用于特定的气动外形以及制导律，但对于不同型号或采用不同制导律的目标需要重新进行推导；文献[15]研究了与HGV类似的机动再入飞行器(MaRV)跟踪问题，为弹道系数构建维纳过程模型，通过动力学反解得到弹道系数的伪量测，从而对其进行最优估计，但该方法对动力学模型进行了高度简化，难以应用于复杂模型。总之，在HGV的跟踪问题中，通常采用维纳过程、马尔可夫过程等统计模型对机动加速度进行建模，并采用扩维卡尔曼滤波进行状态估计，通过强跟踪或交互多模型方法增强滤波器的鲁棒性。然而，单一跟踪模型往往存在选参问题；若采用交互多模型手段增强鲁棒性，则又会产生较大的计算开销，不利于实时跟踪。此外，已有研究工作多基于传统雷达测量，涉及天基观测的研究工作尚为少见。

针对现有工作的不足，本文研究了天基红外观测背景下存在未知时变机动的HGV目标跟踪问题，提出了一种基于机动观测器补偿的鲁棒扩展卡尔曼滤波(Maneuver observer compensated robust extended Kalman filter, MOCREKF)。构造机动观测器，对HGV目标气动加速度进行实时估计，并推导了该机动观测器的误差界；利用机动观测器的输出信息修正扩展卡尔曼滤波的动力学预测步骤，解决模型失配的问题；为克服机动观测器中低通环节带来的时延误差，在扩展卡尔曼滤波的更新步骤引入次优渐消因子，增强滤波器的鲁棒性。通过HGV典型跟踪场景进行仿真对比，验证了MOCREKF相对于现有算法在跟踪精度、鲁棒性和实时性上的优势。

1 HGV滑翔段动力学模型

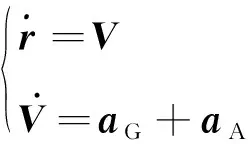
(1)

式中：为引力加速度向量；为气动加速度向量。

HGV滑翔飞行时间相对较短(约500～3000 s)，在引力加速度中仅考虑二体引力和摄动项，则有

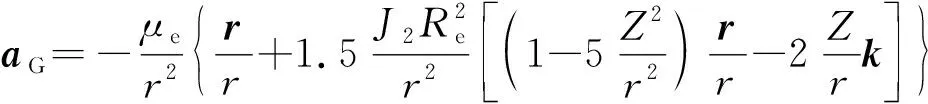
(2)

在速度系下对气动加速度进行解算，HGV的地球相对速度向量为

(3)

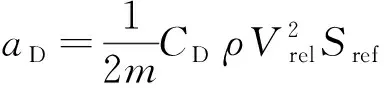
(4)

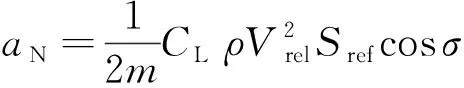
(5)

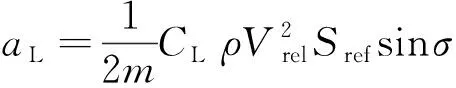
(6)

式中：为HGV质量；,分别为阻力系数和升力系数；为当地大气密度；为地球相对速度的模长；为HGV参考面积；为HGV倾侧角。记气动加速度在J2000惯性系下的坐标分量为A,A,A，则有

(7)

式中：为速度系到惯性系的变换矩阵，根据HGV的位置向量和地球相对速度计算得到。至此，已得到式(1)中和的表达式。

气动加速度向量即为HGV目标根据制导和控制指令生成的机动加速度，通过调整，可产生不同类型的滑翔弹道。对于非合作HGV目标，未知，在目标跟踪过程中必须予以相应的处理。

2 天基红外立体观测模型

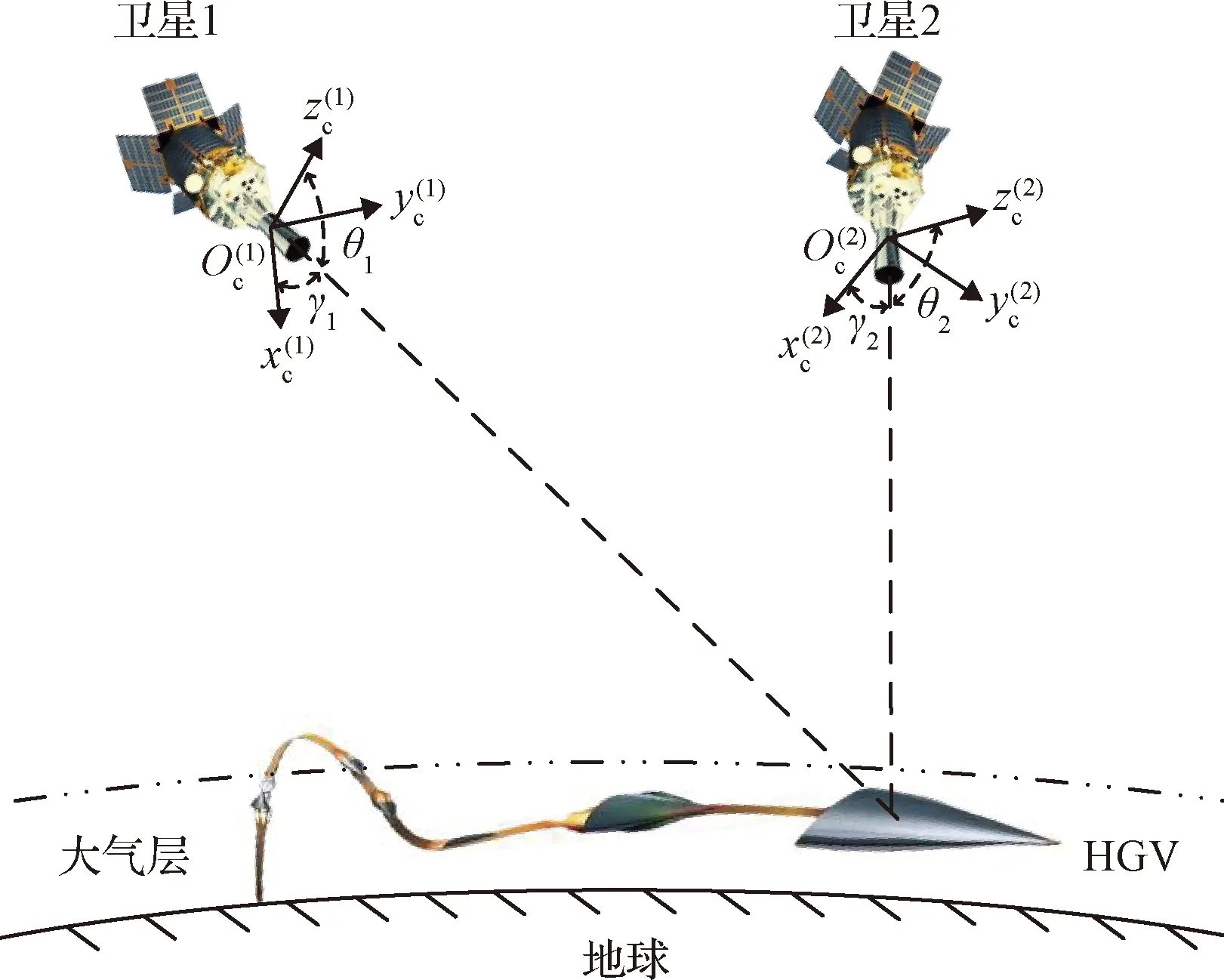
图1 天基红外观测模型Fig.1 Model of space-based infrared measurement

2.1 量测方程

在不影响结论的前提下进行简化，假定各卫星对视线角度,(=1,…,，为协同观测的卫星数目，后文假定≥2)的测量信息被转换至J2000惯性系下，则卫星的视线角度量测方程为

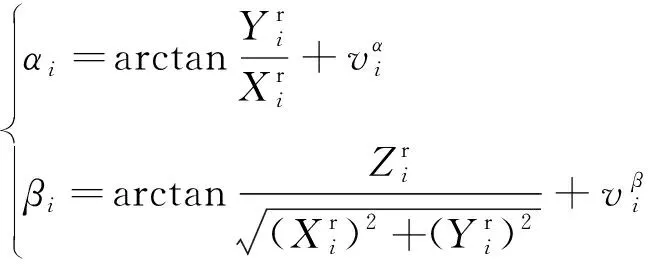
(8)

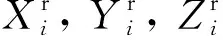
(9)

(10)

式(8)右侧第一项对时间求导，可得到卫星的视线角度变化率量测方程

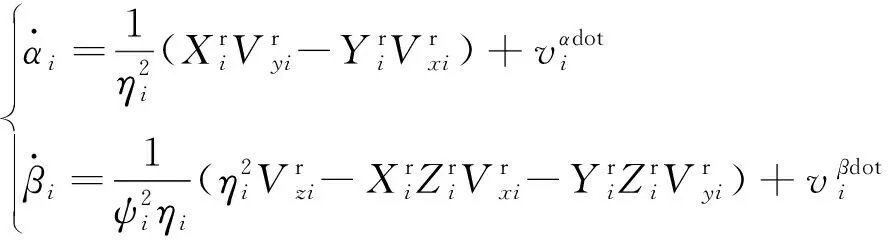
(11)

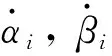
2.2 目标位置速度反解

为便于后续机动观测器的设计，需根据测角信息反解目标的位置及速度。忽略式(8)右侧的量测噪声，不考虑卫星自身星历误差，综合颗卫星的测量信息，可整理得到关于目标位置的方程组

·=

(12)

式中：系数矩阵及列矩阵的表达式为

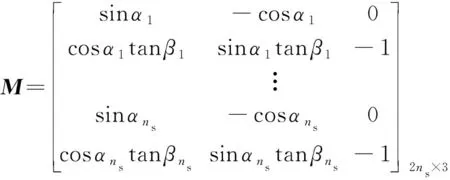
(13)

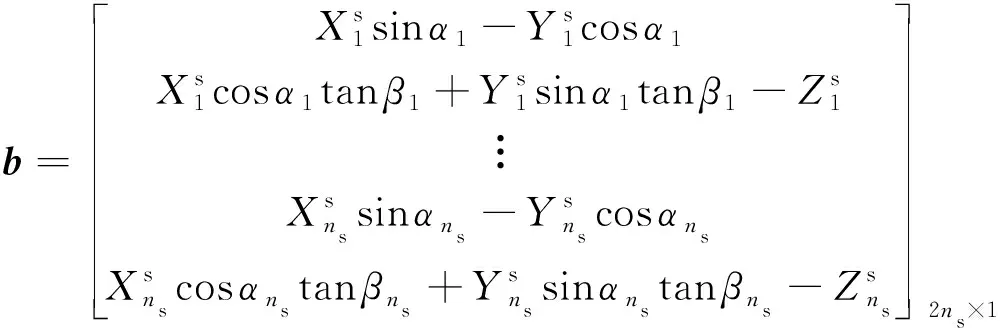
(14)

方程组(12)中存在冗余测量信息，采用最小二乘法可求解得到受噪声污染的目标位置

(15)

忽略量测方程(11)右侧的噪声项，同样不考虑卫星自身星历误差，综合颗卫星的视线角变化率测量信息，可整理得到关于目标速度的方程组

·=

(16)

式中：系数矩阵及列矩阵的表达式为

(17)

(18)

(19)

受量测噪声的影响，从角度和角度变化率量测信息中求解出的目标位置和速度精度较差，仅用于构建机动观测器。为了结合动力学模型对目标位置和速度进行最优估计，应当将式(8)和(11)给出的量测信息输入至滤波器。

3 机动观测器

目标实施机动时，若机动信息已知，则常规滤波器即可达到较好效果；若机动信息未知，跟踪模型与目标实际运动模型的失配将导致滤波器跟踪发散。针对目标的未知机动，本节设计一种机动观测器，从量测中提取目标的机动估计信息，从而抑制滤波发散、提高跟踪精度。

3.1 模型离散化

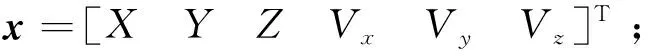
+1=()++

(20)

=()+

(21)

记为自然数集，为实数空间，以上两式中：∈为时间步数；,,分别为时刻的状态向量、量测向量及未知输入向量；∈为输入驱动矩阵；∈为噪声驱动矩阵，取值与相同；∈为零均值高斯过程噪声，反映建模及离散化误差；∈为零均值高斯量测噪声；()由动力学方程(1)离散化得到；()联立了两颗卫星如式(8)、(11)所示的量测方程。在此情况下，任意时刻的均趋近于常值=[05T]，其中为单位阵，为采样周期。后文在必要时以常值代替，并省略单位阵的维度下标。后续机动观测器和滤波器的设计及误差分析均基于离散化的状态空间模型(20)、(21)展开。

“放心吧，现在什么事情也不会有。”他说。“这房子是租下的，签着租赁合同。在租赁合同期满之前，从法律上讲这房子是属于咱们的。”

3.2 机动观测器迭代步骤

为对目标的未知机动进行估计，构造机动观测器

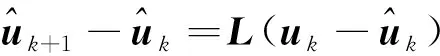
(22)

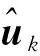
(23)

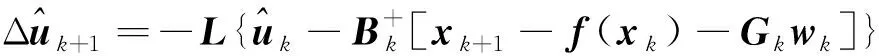
(24)

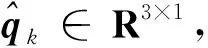
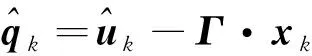
(25)

式中：∈为待定矩阵。将式(25)代入式(24)，合并和+1的同类项，整理得到

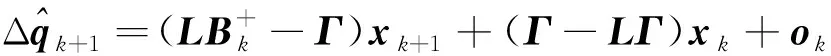
(26)

式中：

(27)

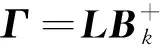
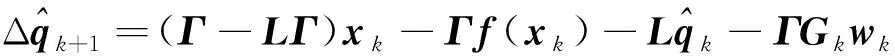
(28)

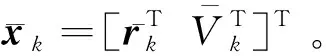
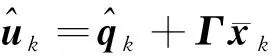
(29)

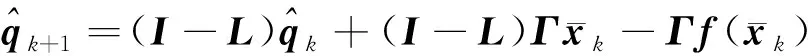
(30)

在递推过程中，该机动观测器仅依赖于当前量测。获取后，等式右侧的各个量均为已知，即可给出目标的未知输入估计。此外，上述推导过程中不存在针对未知输入的假设，因此该机动观测器在使用中无需获取目标机动模式的先验信息，理论上可对目标的各类机动模式进行自适应估计。

3.3 机动观测器误差分析

本节将对机动观测器的误差传播特性进行分析，确定增益矩阵的取值范围，并给出机动观测器的误差界。将机动观测器的误差定义为

(31)

将式(29)代入上式，得到

(32)

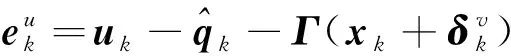
(33)

结合式(20)和式(30)，上式可展开为

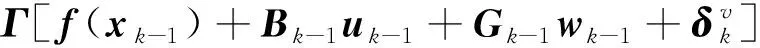
(34)

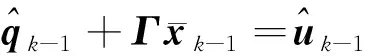
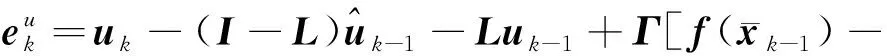
(35)

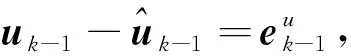
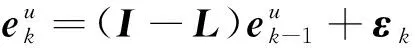
(36)

式中：

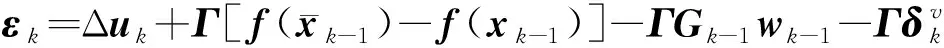
(37)

式(36)描述了机动观测器的误差传播特性，易知项有界。故机动观测器误差收敛的必要条件为

|1-|<1 (=1,2,3)

(38)

上式给出了机动观测器增益矩阵的取值范围。

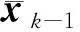
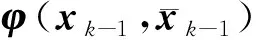
(39)

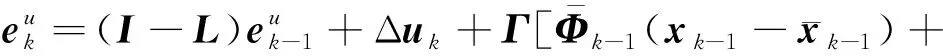
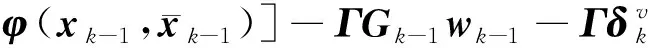
(40)

在式(38)的前提下，当→∞时，有

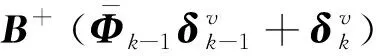
(41)

对于本文研究的问题，有以下条件成立：

(1) HGV在滑翔飞行过程中，其气动加速度连续，未知输入的变化率存在上界，即

(42)

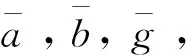
(3) 存在正实数,，使得

(43)

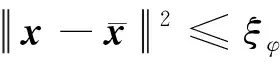
依据条件(1)，对于式(41)右侧第一项，有

(44)

因此

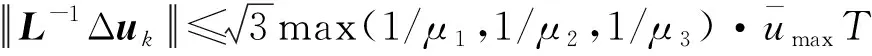
(45)

依据条件(2)和(3)，对于式(41)右侧第二项，有

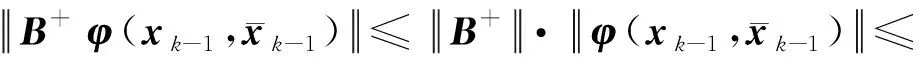
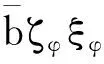
(46)

对于式(41)右侧第三项，有

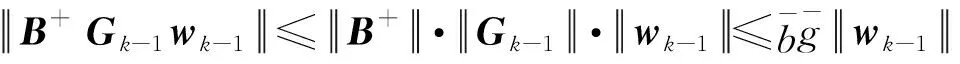
(47)

由于假定-1服从高斯分布，取其3上界，则

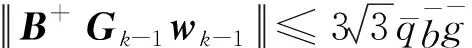
(48)

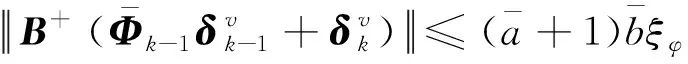
(49)

据此，由矩阵范数性质

(50)

可知，对于式(41)所示的机动观测误差，有

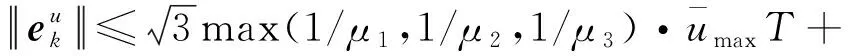
(51)

上式给出了机动观测器的误差界。

3.4 噪声抑制

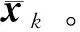
(52)

式中：为时间常数，决定了该环节的通频带宽=1。当过小时，惯性环节对噪声分量的抑制作用不明显；当过大时，该环节会产生较强的时滞，有可能导致滤波发散。受结构强度、热防护等条件约束，HGV的机动频率无法产生较大变化。在实际应用中，可根据HGV的常规机动频率选取。

4 基于机动观测器的鲁棒扩展卡尔曼滤波

将机动观测器的输出作为未知机动估计补偿至扩展卡尔曼滤波的预测步骤中，即可对式(20)、(21)所示的非线性系统进行状态估计。当目标进行快速时变机动时，低通环节(52)将会产生不可忽略的时延误差。为克服时延误差、进一步提高滤波算法的鲁棒性，在扩展卡尔曼滤波的更新步骤中引入次优渐消因子。MOCREKF主要分为初始化、状态预测、渐消因子计算、状态更新和观测器更新五个步骤。

(1)初始化

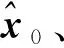
(2)状态预测

计算状态预测

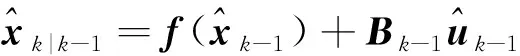
(53)

(3)渐消因子计算

计算渐消因子

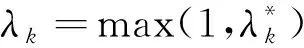
(54)

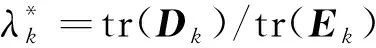
(55)

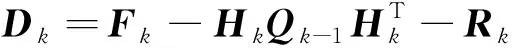
(56)

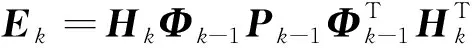
(57)

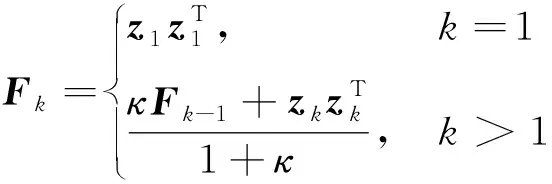
(58)

(4)状态更新

利用渐消因子对先验方差进行调整，有

(59)

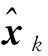
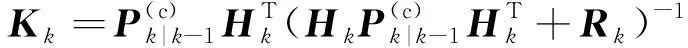
(60)

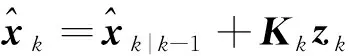
(61)

(62)

式中：为MOCREKF的滤波增益矩阵。

(5)观测器更新

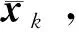
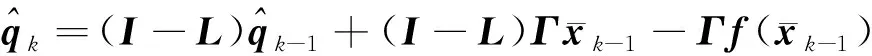
(63)

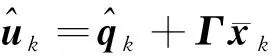
(64)

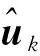
式(53)～(64)构成了MOCREKF的迭代流程，算法结构如图2所示。初始化完毕后，重复执行步骤(2)～(5)，即可实现对HGV目标的轨迹跟踪。不同于扩维卡尔曼滤波、交互多模型滤波等方法，MOCREKF无需使用目标机动的先验信息，理论上对各类机动模式均具备良好的自适应能力，渐消因子的引入也使滤波器具备了较强的鲁棒性。此外，MOCREKF仅在单个扩展卡尔曼滤波器的基础上添加了观测器更新步骤和渐消因子计算步骤，与多模型滤波方法相比具有更低的计算负担。

图2 MOCREKF算法流程Fig.2 Algorithm flowchart of MOCREKF

5 仿真校验

现构建HGV目标的天基观测仿真场景，对本文提出的MOCREKF算法进行性能验证。根据HTV-2相关参数设计跳跃滑翔弹道和拟平衡滑翔弹道，如图3所示，代表两类典型机动模式。目标在(121°E, 52°N)上空约60 km高度处进入滑翔段，初始速度设置为6.5 km/s，在30～60 km高度范围内向西南方向飞行。构建搭载高精度凝视红外传感器的低轨星座，采用Walker构型，卫星总数为200颗，均匀分布在20个500 km高度轨道上。由于单个卫星观测时长受限，仿真过程中采用星间接力的方式进行持续跟踪。协同观测的卫星数目为=2，始终选取对目标可见且基线最佳的观测组合，忽略目标捕获过程中的误差以及卫星自身的定轨误差。依据现阶段传感器精度水平，单星方位角和俯仰角测量标准差选取为5×10rad，角度变化率测量标准差选取为5×10rad/s。滤波跟踪总时长为1400 s，离散周期为=1 s，滤波器过程噪声标准差置为0.01 m/s。

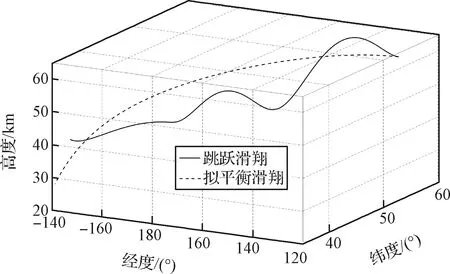
图3 HGV滑翔段弹道Fig.3 Trajectory of HGV in glide phase

作为对比，采用强跟踪滤波(Strong tracking filter, STF)、扩维卡尔曼滤波(Augmented state Kalman filter, ASKF)、交互多模型(Interactive multiple model, IMM)滤波以及本文提出的MOCREKF分别对HGV目标进行跟踪。文献[9]对标准卡尔曼滤波跟踪机动目标时出现的发散现象进行了详细的仿真和分析，故此处不再采用标准卡尔曼滤波进行对比。各跟踪算法中，ASKF的加速度分量采用一阶马尔可夫模型描述，在不使用先验信息的情况下将机动频率参数设定为0.3和1，分别记为ASKF1和ASKF2。在交互多模型滤波中，设计五个扩维子模型，机动频率参数在区间[0,1]内等间隔选取。在MOCREKF中，根据式(38)将观测器增益矩阵选取为=diag(1, 1, 1)，低通环节时间常数选取为=20。各个滤波器的位置、速度初值根据初始时刻的测量信息求解得到，机动估计初值置为零。

5.1 场景一：拟平衡滑翔弹道跟踪

在拟平衡滑翔过程中，目标机动加速度变化较为平缓。分别采用STF, ASKF1, ASKF2, IMM, MOCREKF对图3中的拟平衡滑翔弹道进行跟踪，在i7-1185G7, 32G RAM, MATLAB环境下执行1000次蒙特卡洛仿真，得到位置、速度、加速度估计的均方根误差(RMSE)曲线，分别如图4～图6所示。绘制单次仿真中的观测器输出曲线，如图7所示。统计各算法平均单步RMSE及平均单步运行耗时，见表1。

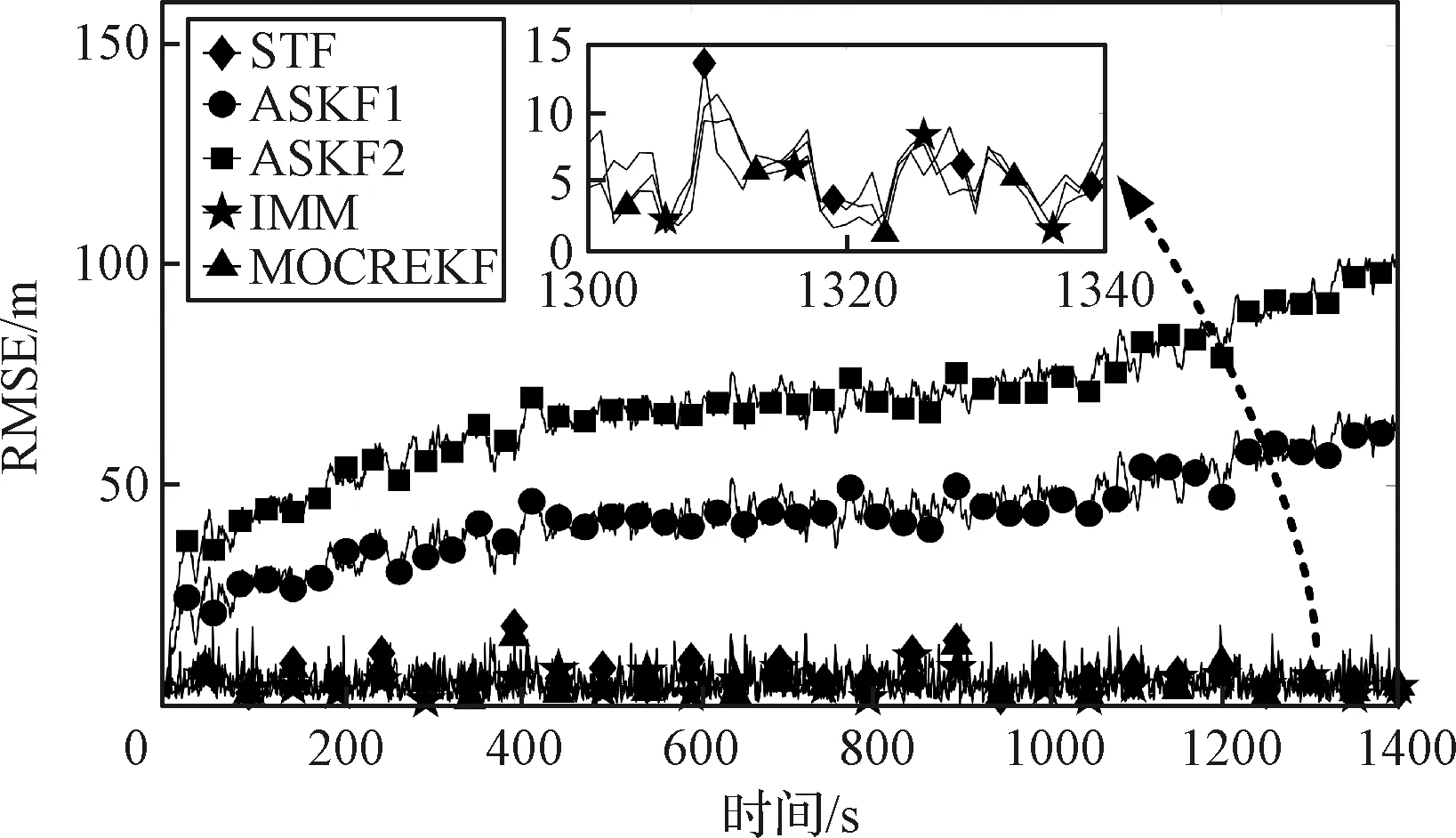
图4 位置RMSE(场景一)Fig.4 Position RMSE (Scenario 1)

图5 速度RMSE(场景一)Fig.5 Velocity RMSE (Scenario 1)

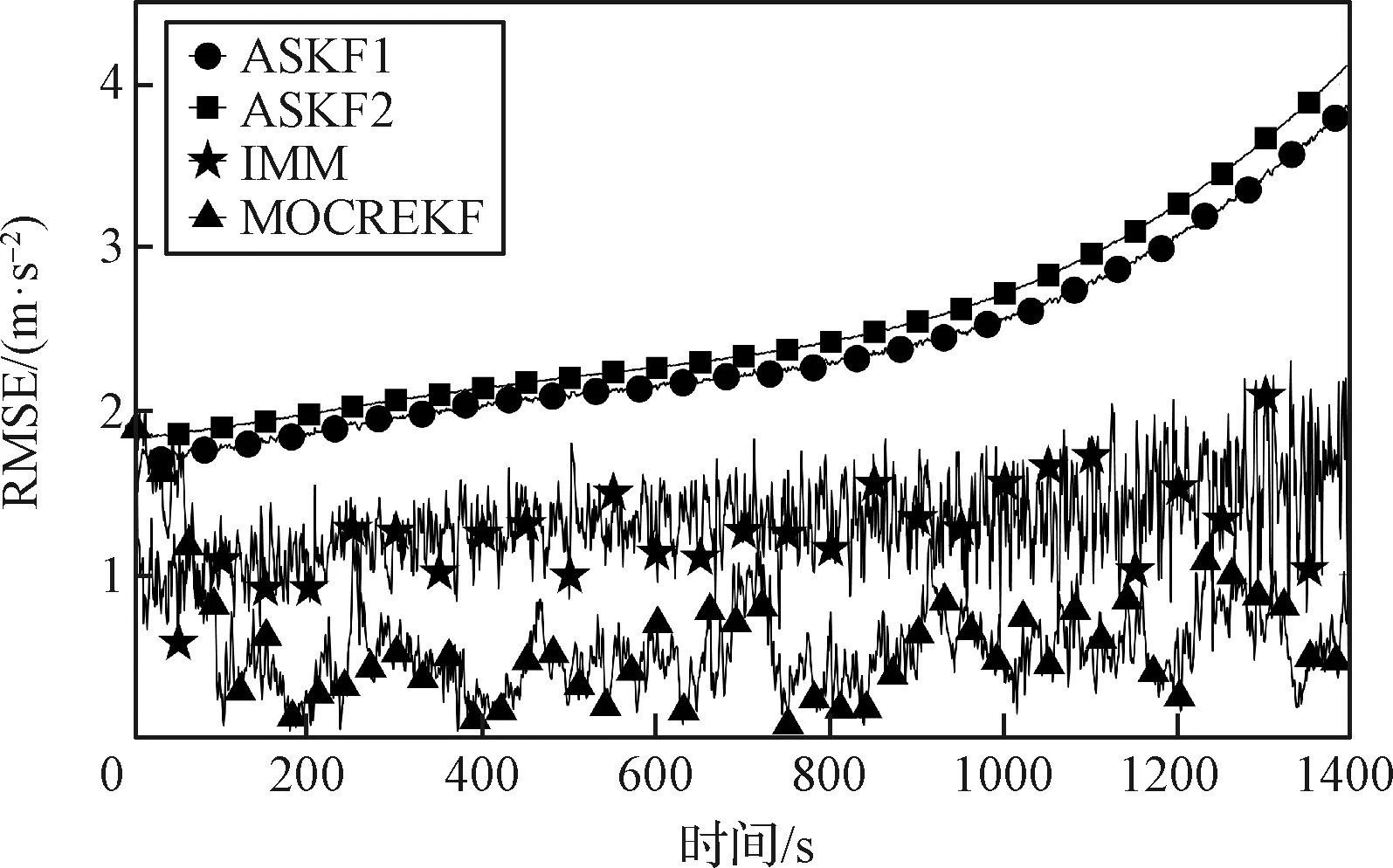
图6 机动加速度RMSE(场景一)Fig.6 Maneuver acceleration RMSE (Scenario 1)

图7 观测器机动加速度估计(场景一)Fig.7 Maneuver acceleration estimation of the observer (Scenario 1)

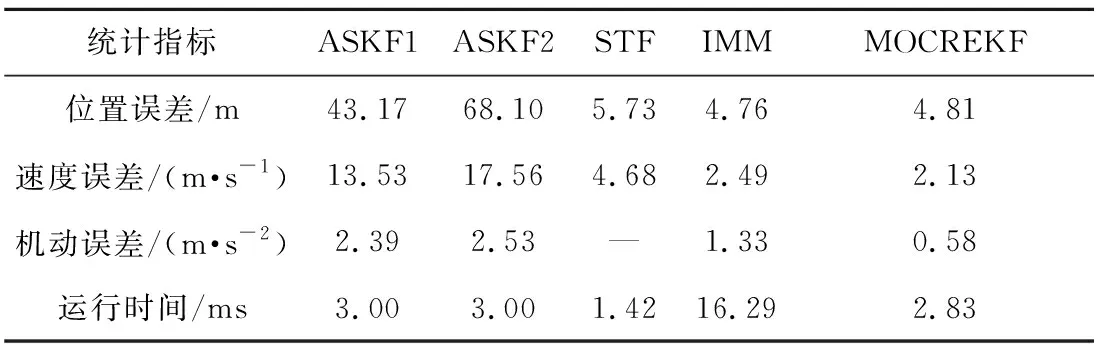
表1 各滤波器平均RMSE及耗时(场景一)Table 1 Average RMSE and computing time of filters (Scenario 1)

观察图4、图5可知，在不使用目标机动先验信息时，难以对扩维卡尔曼滤波中的机动模型参数(机动频率)进行合理取值，致使单模型ASKF1, ASKF2跟踪发散。在对目标机动规律进行充分分析的前提下，方能在马尔可夫过程、维纳过程等机动模型中给出合理的参数取值，但在多数情况下目标的机动信息难以事先获取。STF根据渐消因子对方差进行修正，强迫滤波器收敛；IMM滤波对多个机动模型的输出结果进行融合，利用模型集对目标可能的机动模式进行覆盖；MOCREKF在使用机动观测器修正跟踪模型的同时，进一步利用渐消因子增强滤波器的鲁棒性。在图4和图5中，STF, IMM, MOCREKF均取得了良好的效果，收敛到了相似的误差下界。但STF的速度估计误差略高于IMM和MOCREKF。

观察图6可知，ASKF1, ASKF2在机动加速度方面也无法给出准确的估计。STF仅通过方差膨胀迫使滤波器收敛，不具备机动加速度估计的能力。尽管IMM的加速度估计误差显著低于ASKF1和ASKF2，但受模型集中失配模型的影响，其加速度的估计误差仍然较高，且存在轻微的发散趋势。与IMM相比，MOCREKF能够给出精度更高、收敛性更为良好的加速度估计。观察图7可知，本文所设计的机动观测器能够较好地逼近机动加速度真值。

由表1可知，本文提出的MOCREKF在精度上优于ASKF和STF，与IMM相近。然而MOCREKF在计算耗时上远低于IMM，这是因为MOCREKF未进行扩维处理，仅在标准EKF的基础上添加了观测器和渐消因子递推步骤，其运行耗时与单模型扩维卡尔曼滤波器相近。IMM中包含五个扩维子模型以及模型交互步骤，故其运行耗时约为单模型扩维卡尔曼滤波器的五倍。

5.2 场景二：跳跃滑翔弹道跟踪

与拟平衡滑翔相比，HGV在跳跃滑翔过程中的机动加速度变化较为频繁。各滤波器配置同场景一，采用STF, ASKF1, ASKF2, IMM及MOCREKF对图3中的跳跃滑翔弹道进行跟踪，执行1000次蒙特卡洛仿真，得到位置、速度、加速度的RMSE曲线，分别如图8～图10所示。绘制单次仿真中的观测器输出曲线，如图11所示。统计各算法平均单步RMSE，见表2。

观察图8、图9可知，单模型滤波器ASKF1和ASKF2均由于模型失配而产生发散，无法给出准确的状态及机动加速度估计。STF, IMM及本文提出的MOCREKF在位置和速度估计上具备较好的收敛性。观察图10可知，MOCREKF具有比IMM更高的机动加速度估计精度，这与场景一的结论具有一致性。观察图11可知，MOCREKF中的机动观测器在跳跃滑翔机动模式下同样能够较好地逼近目标加速度真值。由表2数据可知，在场景二中MOCREKF的精度仍然高于STF，且与IMM保持在相同水平。

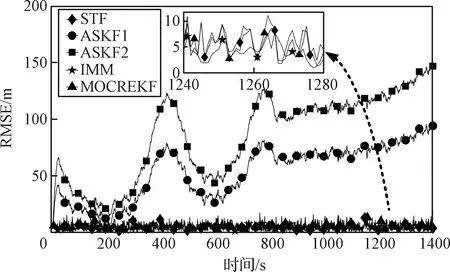
图8 位置RMSE(场景二)Fig.8 Position RMSE (Scenario 2)

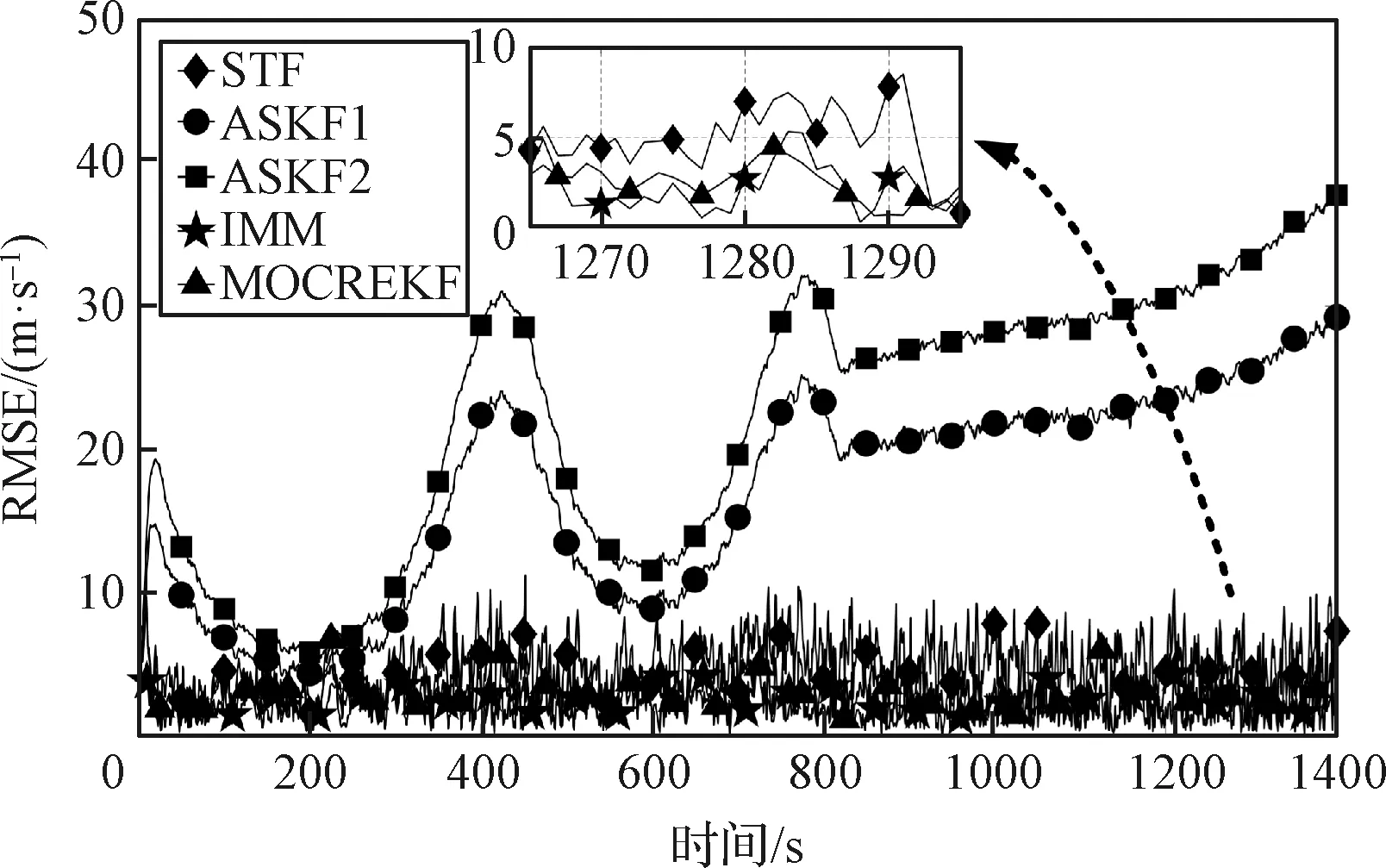
图9 速度RMSE(场景二)Fig.9 Velocity RMSE (Scenario 2)

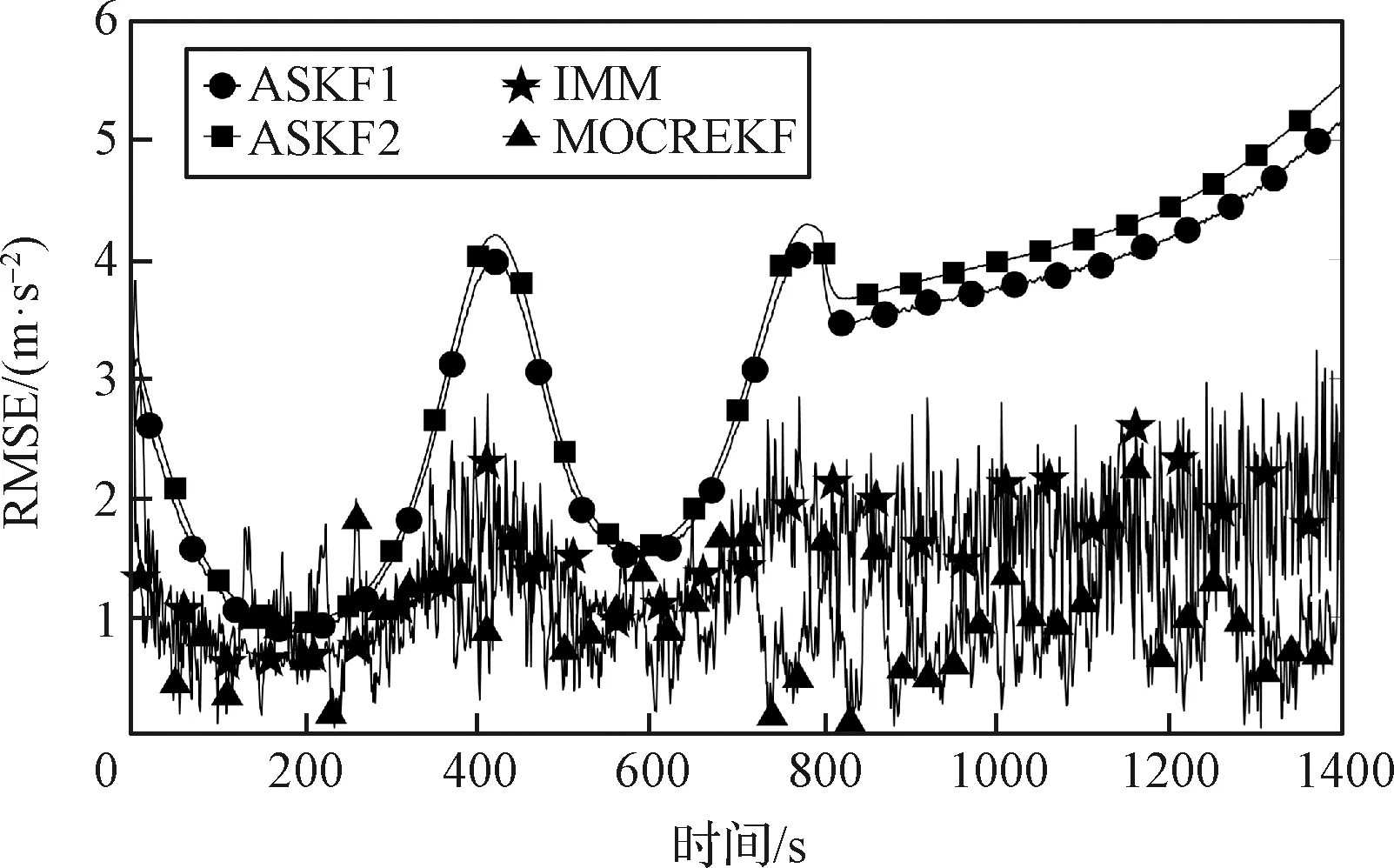
图10 机动加速度RMSE(场景二)Fig.10 Maneuver acceleration RMSE (Scenario 2)

图11 观测器机动加速度估计(场景二)Fig.11 Maneuver acceleration estimation of the observer (Scenario 2)

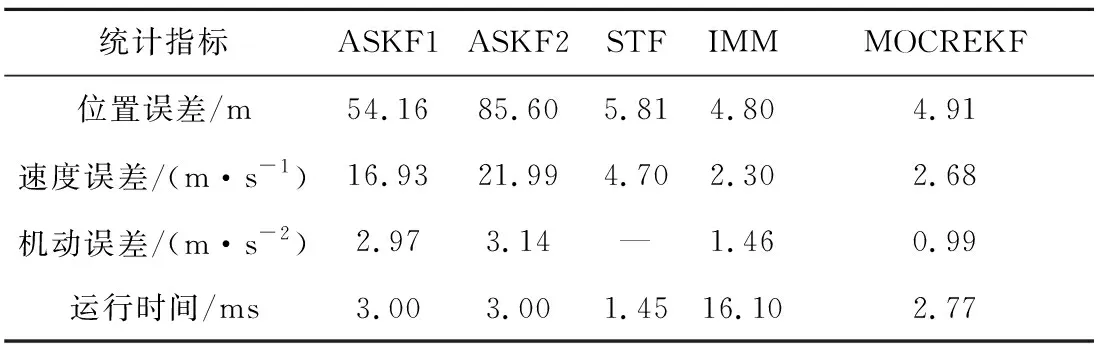
表2 各滤波器平均RMSE及耗时(场景二)Table 2 Average RMSE and computing time of filters (Scenario 2)

前文机动观测器设计过程中未使用HGV目标机动的任何先验信息，其机动估计能够自适应地逼近目标机动真值，故MOCREKF对HGV目标的机动模式不敏感。在场景一和场景二所代表的两类典型机动模式下，MOCREKF无需调整滤波器结构及参数，均能够以较低的计算开销取得收敛性良好、精度较高的HGV目标状态及机动加速度估计。

6 结 论

为解决存在未知时变机动的HGV目标轨迹跟踪问题，设计机动观测器估计目标的未知机动，并提出了一种MOCREKF。拟平衡滑翔和跳跃滑翔两类典型机动场景的仿真分析表明：

(1) 本文所提MOCREKF中的机动观测器可根据测量信息有效提取出目标的机动估计，与强跟踪滤波、扩维卡尔曼滤波相比，MOCREKF在HGV目标跟踪问题中具有更优的稳定性和精度；

(2) MOCREKF设计过程中未使用目标机动规律的先验信息，在场景一和场景二中均表现出良好的性能，对目标的机动模式具有较强的鲁棒性；

(3) MOCREKF的实时性良好，其计算负担大致与单模型扩维卡尔曼滤波相同，远低于相同精度水平的交互多模型滤波。