索式火箭回收着陆系统缓冲装置设计与分析

张 欢,张 成,宋晓东

(1. 北京理工大学宇航学院,北京 100081； 2. 北京理工大学飞行器动力学与控制教育部重点实验室,北京 100081)

0 引 言

发展可重复使用火箭具有满足未来空间开发、降低发射成本等重要意义,一直是国内外航天领域的热点和焦点。目前,在众多的可重复使用火箭回收技术方案中,着陆腿式垂直动力回收火箭是发展最迅速的回收方式。特别是在美国的商业航天公司SpaceX和蓝色起源分别多次成功回收猎鹰9火箭和New Shepard火箭的一级后,着陆腿式垂直动力回收方案成为世界各大航天大国争先发展的技术途径。然而,这种回收方式需要严格限制火箭着陆状态的偏差范围及与之对应的技术问题,制约了中国可重复使用火箭技术快速发展。

火箭若以着陆腿式垂直动力回收方式着陆,需要以接近零的速度和垂直姿态到达着陆平面,才能保证回收的成功。这样严格的火箭着陆状态偏差限制需要箭上的软硬件技术来支持。具体来说,发动机的推力需要具有大范围的调节能力和多次启动的能力,使得火箭到达着陆平台时趋近于静止,以实现软着陆。大范围调节发动机的推力,对发动机燃烧、涡轮泵、阀门等组件要求较高,需要具有较宽范围推力调节的发动机系统配置。火箭在返回过程中,需要对其姿态不断进行控制调整,并在着陆前调整为垂直状态,在着陆末段减少大气、尾流等干扰对着陆过程造成的影响,使其精准到达着陆点,着陆过程的垂直姿态和高精准落点需要火箭的导航制导控制系统的技术支持。另外,着陆腿具备缓冲着陆冲击的能力和对倾斜姿态与横向速度偏差的纠正能力的要求,同样需要着陆腿相应技术支持。国内外相关领域的专家就着陆腿式回收着陆技术进行了深入的研究,积累了大量的理论和试验技术。除了用于可重复使用火箭回收着陆外,着陆腿亦被用于火星着陆器和月球着陆器的着陆,着陆腿着陆的设计与优化经历了近半个世纪探索与研究,中国在此方面也取得了非凡的成就,成为了第二个在火星上登陆并运行航天器的国家。然而,自2015年末SpaceX第一次成功回收猎鹰9火箭子级以来,仍然只有SpaceX和蓝色起源两家航天公司能够回收并重复使用火箭,采用着陆腿式火箭回收着陆方式的多家航天机构的研究进度仍然处于立项或试验阶段。

近两年,国内外航天科研人员相继提出一些新型的火箭回收着陆方式。一种转换的思想是：将火箭着陆状态偏差范围的限制放宽,箭上的回收着陆技术难度转移到地面,利用地面回收着陆装置回收火箭。2020年,作者和清华大学任革学教授等提出了一种地面火箭回收索系统。该系统在地面搭建的塔架上布置可移动回收索,主动跟随捕获具有较大的着陆位置偏差和姿态偏差的着陆火箭；将挂钩设置在火箭中部,弹性挂钩挂在回收索后,带动回收索继续向下减速缓冲,由于火箭级段的燃料在着陆阶段几近消耗殆尽,着陆火箭重心偏下使得减速缓冲过程火箭呈现单摆稳定构型,保证了着陆的稳定性；系统的减速缓冲装置由配重和摩擦滑道组成,能够对重量为2.5×10kg和着陆垂直速度为20 m/s的火箭级段进行减速缓冲,火箭减速为零时配重与滑道的静摩擦保证了火箭的最终静止稳定。然而这种减速缓冲方式的缓冲能力和火箭减速运动学特性调节能力有限,回收不同的着陆火箭需要重新配置减速缓冲装置。随着火箭子级逐渐增大的发展趋势,有必要设计一种具有自动调节能力和强缓冲能力的火箭回收着陆系统。采用同样的转换思想的还有SpaceX的星舰回收,数十次的回收试验表明着陆腿的缓冲能力明显不足以回收大型的星舰,因此SpaceX摒弃箭上着陆腿,提出了利用发射架上机械臂直接捕获着陆火箭的回收着陆方案,以此来降低箭上着陆腿等回收装置质量和获得更大的缓冲能力。

本文在文献[21]的火箭回收索系统基础上进行优化设计,借鉴舰载机拦阻索系统的液压减速缓冲装置,以火箭减速缓冲的目标运动学特性为给定参数,基于最小二乘法反问题设计思路设计液压减速装置的控制阀凸轮外形,使火箭在给定的缓冲位移限制下安全稳定的着陆。最后,基于ALE(Arbitrary Lagrangian Eulerian formulation)索描述建立了系统的精准高效多体动力学模型,并通过仿真计算对所设计索式火箭回收着陆系统的动力学特性进行校验,分析系统对不同质量和着陆速度的着陆火箭的减速缓冲能力和自动调节能力。

1 索式火箭回收着陆系统总体设计

文献[21]中的地面火箭回收索系统利用配重和配重与滑道之间的摩擦力作为火箭减速缓冲过程的主要阻力,然而这种减速缓冲装置是针对特定的着陆火箭设计的。针对不同质量和着陆速度的着陆火箭,该减速缓冲装置需要重新配置配重与滑道之间的法向力来调节配重与滑道之间的摩擦力,同时调整配重质量,实现系统对不同着陆火箭的减速缓冲能力的调节。针对特定的系统,若火箭着陆时的质量超过设计值时,减速缓冲装置的缓冲能力不足,极有可能发生火箭与地面碰撞导致回收失败。为了实现对不同质量和着陆速度的着陆火箭的自动调节缓冲能力,同时为了适用大型火箭子级的回收着陆,本文将文献[21]中火箭回收索系统改进设计为索式火箭回收着陆系统,重点设计减速缓冲装置实现系统的可自动调节的大缓冲能力。

索式火箭回收着陆系统,如图1所示,由塔架、导轨、滑块、滑轮、一根回收索、一根传递索和减速缓冲装置组成。四个导轨围成正方形回收区域,边长为2=50 m。在塔架的上方,一根回收索绕过若干滑轮形成一个网状的捕获框(图1中紫色区域)。在其中一个塔架上引出回收索,通过滑轮组与地面的减速缓冲装置中的连接索连接,减速缓冲装置采用液压式。与文献[21]中的地面火箭回收索系统相比,本文将系统回收索由4根改为1根并简化了布线方式,将减速缓冲装置由4个改为1个,使得捕获框的索张力在减速缓冲过程中基本一致,避免火箭发生倾斜,并减速缓冲装置改为液压式,用来提高缓冲能力和自动调节能力。

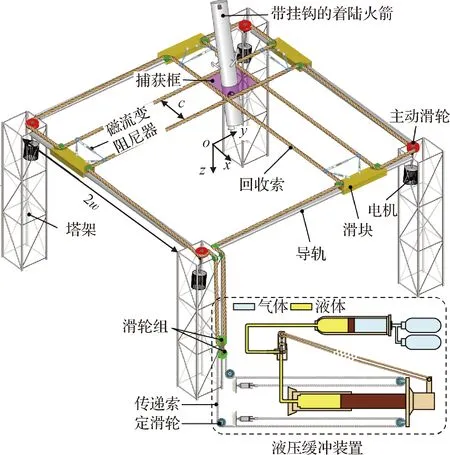
图1 索式火箭回收着陆系统Fig.1 Cable system for rocket recovery landing

索式火箭回收着陆系统回收着陆火箭可分为主动跟随捕获阶段和被动减速阶段,如图2所示。在主动跟随捕获阶段,电机驱动主动滑轮带动滑块在导轨上滑动,进而实现捕获框在平面移动,图3为四个电机驱动的主动滑轮的转向和捕获框的位移的关系。直到火箭进入捕获框并将挂在捕获框上,电机关机,回收着陆流程进入被动减速阶段。具有垂直速度的火箭带动回收索继续向下运动,进而拖拽传递索向上运动,液压减速缓冲装置中的柱塞向主液缸内滑动产生阻力,从而实现对火箭的减速缓冲。在着陆火箭上,由于火箭重心偏下,在火箭中部周向安装四个弹性挂钩。在被动减速阶段,火箭的挂钩挂在回收索上呈现单摆稳定构型,保证减速过程中的稳定性。

图2 火箭回收着陆时序Fig.2 Time sequence of rocket recovery landing

借鉴舰载机拦阻索系统的液压减速缓冲装置设计,本文所设计的索式火箭回收着陆系统的减速缓冲装置亦采用液压式。液压减速缓冲装置具有较强的缓冲能力和自动调节能力,地面火箭着陆减速缓冲装置代替箭上着陆腿缓冲装置,减小了箭上回收装置的质量和实现火箭垂直速度小偏差限制的相关技术难度。液压减速缓冲装置由主液缸、柱塞、动滑轮组、控制阀系统、储能器、冷气瓶组成,如图4所示。传递索绕过柱塞端部的动滑轮和导向滑轮与支架上的滑块连接。主液缸内充满油液,一端与控制阀连接,另一端的开口由柱塞封闭,柱塞可沿着主液缸的轴向滑动。储能器中间由浮动活塞分成两个腔,一端与控制阀连接,腔内充满了油液。另一端与冷气瓶相连,腔内充满了高压空气。控制阀系统由凸轮、活塞、摇臂、节流阀和传动机构组成,如图3所示。凸轮通过传动装置与柱塞相连,柱塞运动带动凸轮转动。凸轮压在摇臂上,带动活塞移动,改变节流阀开口面积,调节流经节流阀的油液流量,改变主液缸的压强,进而调节回收所索张力大小。凸轮的外形与火箭减速缓冲过程的运动学特性直接相关。

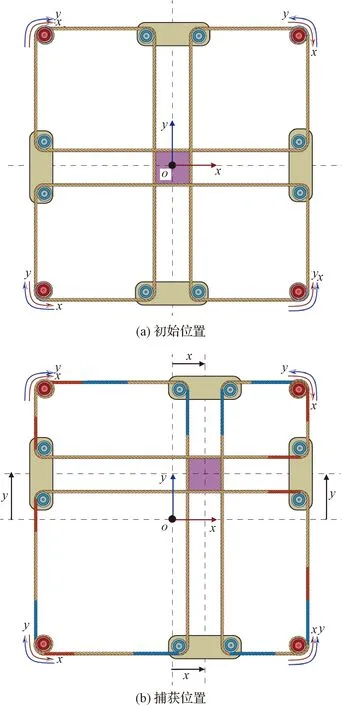
图3 主动滑轮与捕获框的运动学关系Fig.3 Kinematic relation between active pulley and capture frame

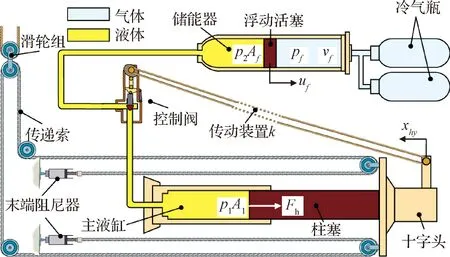
图4 液压减速缓冲装置Fig.4 Hydraulic buffer device

在火箭减速缓冲过程的运动学特性中,火箭减速缓冲阶段的位移不宜过大,以避免其超过挂在回收索上的火箭与地面的距离发生火箭发动机触地爆炸事故；火箭在减速缓冲过程中的加速度也不宜过大,以减少火箭的结构损伤和降低维修费用。为了实现安全回收着陆火箭级段,需要设计满足上述要求的目标火箭减速缓冲运动学响应。然后,在已知运动学特性的前提下,对液压减速缓冲装置的阻力,即对控制阀凸轮的外形进行设计,这是一个典型的反问题设计。

2 火箭减速缓冲运动学特性反问题设计

以火箭减速缓冲过程的目标运动学特性作为给定参数,对索式火箭回收系统的液压减速缓冲装置进行反问题设计的步骤为：(1)设计满足火箭安全回收的减速缓冲运动学响应特性及柱塞的运动学特性；(2)基于索式火箭回收着陆系统和着陆火箭的简化动力学模型求解火箭减速缓冲过程中的反问题目标液压阻力；(3)根据图4和图5中液压减速缓冲装置和控制阀系统的力学模型计算节流阀阀芯位置曲线,基于最小二乘法求解控制阀中凸轮外形的曲线。

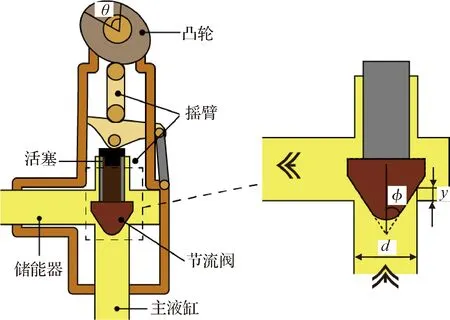
图5 控制阀系统Fig.5 Control valve system

2.1 火箭减速缓冲过程的目标运动学特性

(1)

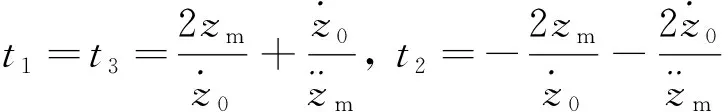
(2)

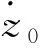
由图4可知,液压减速缓冲装置的阻力与柱塞的运动学特性相关。为了获得火箭与柱塞的运动学关系,建立图6所示的系统简化动力学模型,忽略回收索和传递索的弹性变形并考虑火箭在回收区域中心被捕获。火箭下降距离与柱塞位移之间的关系为

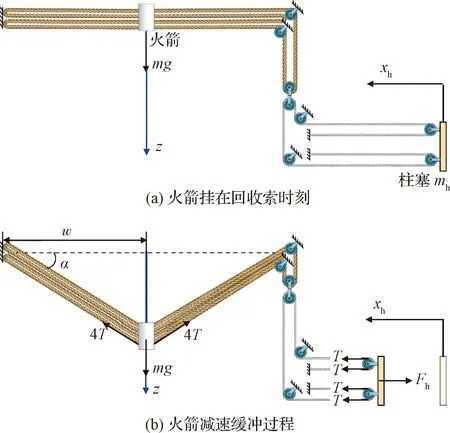
图6 索式火箭回收着陆系统简化动力学模型Fig.6 Simplified dynamic model of the cable system for rocket landing

(3)

式中：为回收区域边长的一半。

对式(3)求导,得到柱塞的速度和加速度分别为

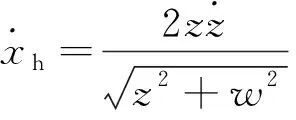
(4)

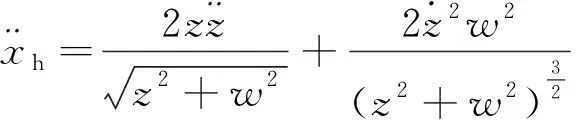
(5)

设计火箭减速缓冲过程的目标加速度、速度和位移由式(1)及其积分和式(2)确定,柱塞的位移、速度和加速度则由式(3)～(5)确定。

2.2 液压减速缓冲装置的目标液压阻力

索式火箭回收着陆系统的动力学模型如图6所示,当忽略回收索和传递索与各滑轮之间的摩擦和滑轮的惯量,各段回收索和传递索的张力相同,令回收索和传递索张力均表示为,作用在柱塞上传递索张力大小为4,则火箭和柱塞的动力学方程为

(6)

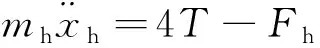
(7)

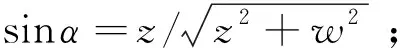
由于回收索布局的对称性,整个系统只有一个自由度。由式(6)和式(7)可得单自由度系统的动力学方程为

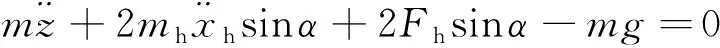
(8)

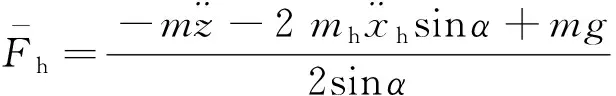
(9)

2.3 基于最小二乘法的控制阀凸轮外形设计

图4中液压减速缓冲装置的柱塞的液压阻力由三部分组成

(10)

式中：,和分别为油液阻力、主液缸与储能器压力差和储能器压力；Δ=-为主液缸与储能器的压强差,为主液缸的压强,为储能器的压强；为油液的阻尼系数；为柱塞的横截面积。

主液缸的油液在柱塞推动下流入储能器的过程中,主液缸的油液压强与流过节流阀的油液流量有关,则主液缸与储能器的压力差可表示为

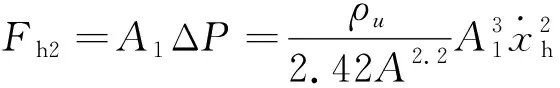
(11)

式中：为油液密度；为节流阀横截面积。

储能器的压强与空气压缩瓶中的气体压强相等,由于气体被压缩过程的时间较短,视为绝热过程,则

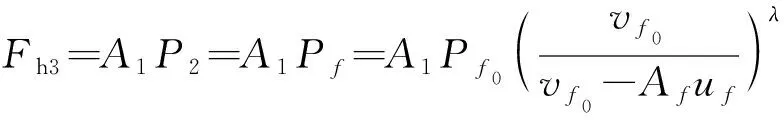
(12)

式中：0为空气压缩瓶的初始压强；0为空气压缩瓶的初始体积；为压缩气体的绝热系数；为储能器活塞的有效面积；这里储能器活塞的位移等于主液缸活塞的位移。

对于确定的柱塞位移和速度,式(3)和式(4),式(5)中的油液阻力和储能器压力也是确定的。主液缸与储能器压力差中,液体密度和柱塞的横截面积为常量,柱塞的速度已知,则柱塞的液压阻力由节流阀的横截面积来控制,对比式(3)和式(4),并考虑式(10),确定目标节流阀横截面积为

(13)

在火箭减速缓冲过程中,柱塞向主液缸内滑移,通过传动机构带动控制阀系统中的凸轮转动,凸轮推动活塞使节流阀的阀芯运动,调节节流阀的开口面积,从而控制油液流量,实现主液缸压强的改变。图5中节流阀小孔的截面积与节流阀的阀芯位置的关系为

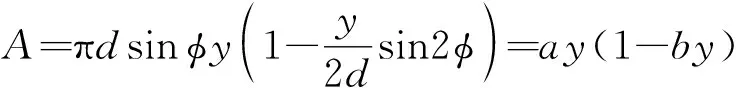
(14)

式中：是节流阀顶角的半角；为主液缸和节流阀的连接处的阀口直径；简化参数分别为=πsin和=sin2(2)。

由式(14)得知,节流阀小孔的截面积只与节流阀阀芯的位置有关。为了简化分析,整合凸轮转角与摇臂长度,阀芯的位置只受到凸轮转角控制

=(1----)

(15)

式中：=10为阀芯的初始位置；,,和是凸轮曲面位形的函数系数。

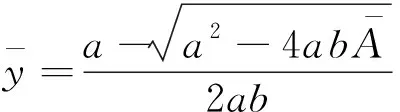
(16)

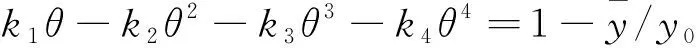
(17)

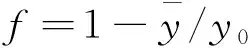
(18)

将式(18)对(=1,2,3,4)求导,得

(19)

将上式整理为未知量(=1,2,3,4)的线性方程组

=

(20)

求解上式(20)线性代数微分方程,求得凸轮的形状系数为

(21)

式中：

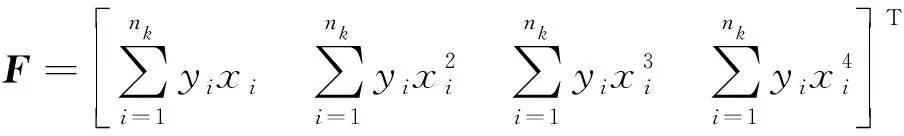
为实现火箭在减速缓冲段按照既定的运动特性运动,液压减速缓冲装置中的凸轮目标形状系数由式(21)确定。

2sin-=0

(22)

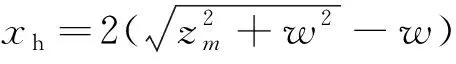
(23)

时,液压减速缓冲装置能保证火箭在减速为零后稳定且不发生反弹脱钩。

(24)

当凸轮转角在1186°≤≤23805°范围内时,凸轮形状曲线系数为

(25)

凸轮的外形轮廓线如图7所示。油液阻力、主液缸与储能器压力差和储能器压力如图8所示。在减速缓冲阶段油液阻力和主液缸与储能器压力差是火箭减速的主要减速缓冲力,而储能器压力用于火箭减速降为零后保持稳定。

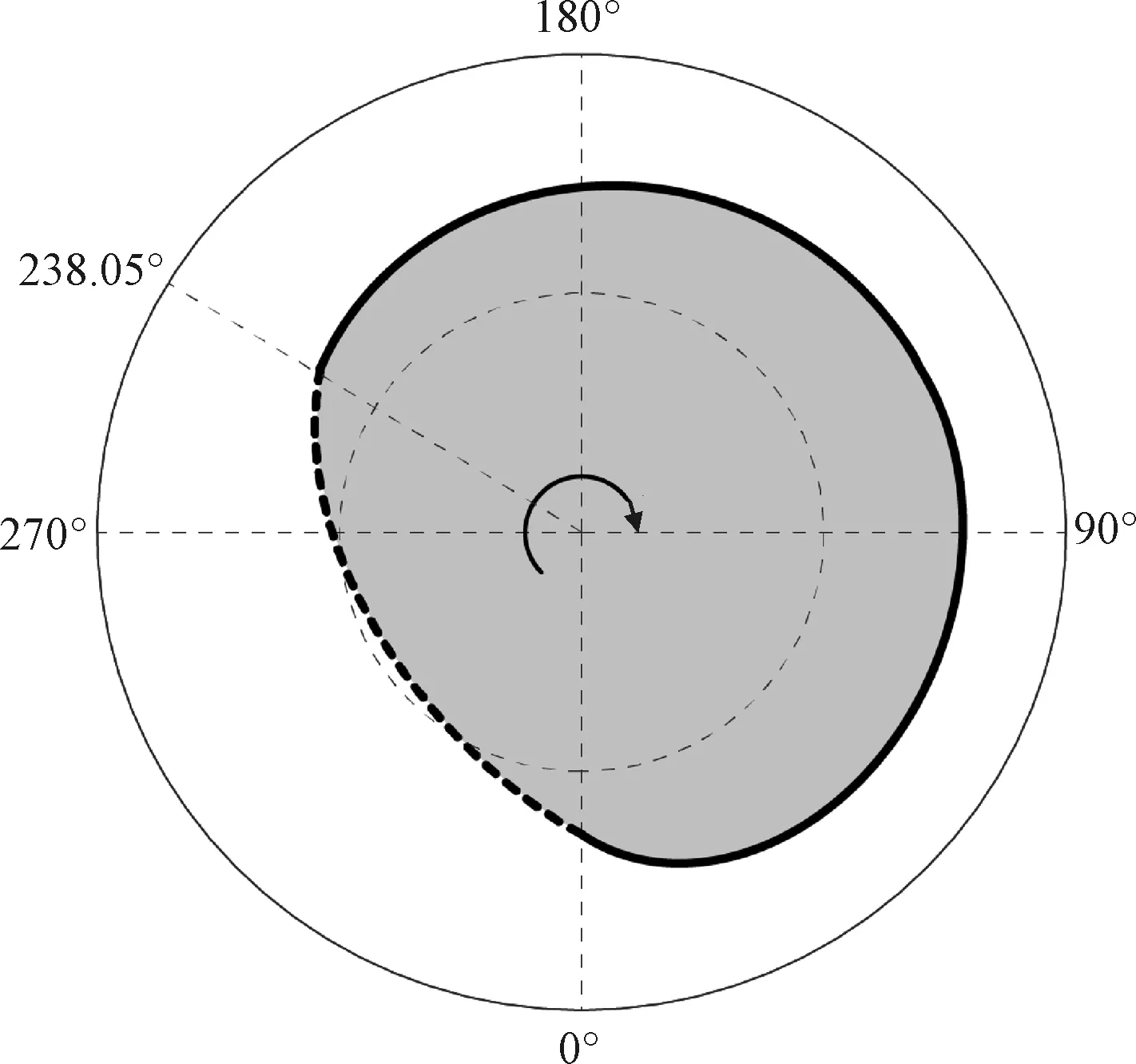
图7 凸轮外形轮廓线Fig.7 Cam profile

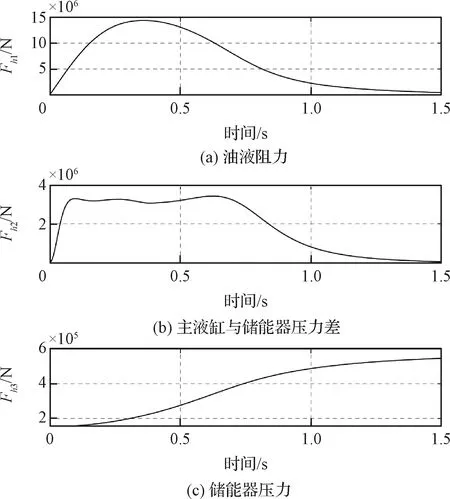
图8 液压减速缓冲装置柱塞的液压力Fig.8 Hydraulic pressure on the hydraulic buffer’s piston

3 多体动力学仿真校验

航天系统设计面临着复杂的动力学耦合问题,采用多体动力学仿真是一种行之有效的方法。索式火箭回收着陆系统在捕获和减速缓冲火箭的过程中,索是主要的承力部件,而索具有典型的几何非线性特性,减速缓冲过程索的振动直接影响整个系统的动力学特性。而液压减速缓冲装置的反问题设计过程中采用的简化动力学模型忽略了索的柔性,并限制了火箭在回收区域的中心着陆。为了校验所设计的液压减速缓冲装置的减速缓冲特性的准确性,有必要建立系统精准的多体动力学模型并进行仿真计算,分析索式火箭回收着陆系统的动力学特性。

3.1 系统多体动力学模型

索式火箭回收着陆系统是一个复杂的刚柔耦合系统。火箭、索、滑轮和滑块相互连接的拓扑形式复杂,又包含大量的索过滑轮接触和挂钩与索的碰撞。为了在保证模型准确性的前提下提高计算效率,本文利用ALE索单元对回收索和传递索进行建模,利用刚体模型对滑块、柱塞和火箭进行建模,对滑块和柱塞建立滑移副约束限制其只有一个平动自由度,重力和液压阻力则建立为系统的广义外力,系统的多体动力学模型如图9所示。

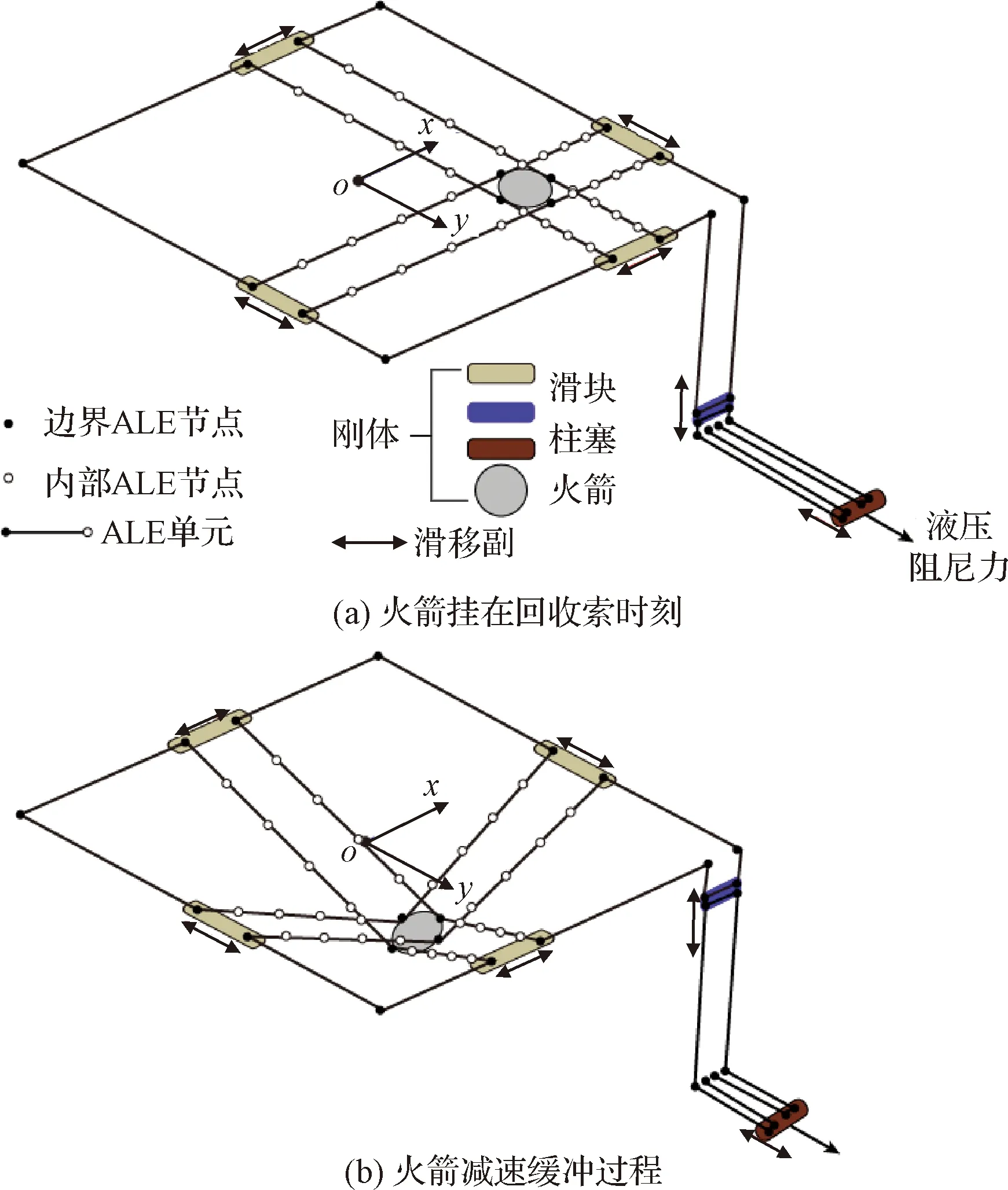
图9 索式火箭回收着陆系统多体动力学模型Fig.9 Multibody dynamics model of the cable system for rocket landing

利用ALE索节点的物质坐标与空间网格坐标的独立性,将索过滑轮的接触和挂钩与索的接触均由一个ALE索节点来建模,约束ALE索节点与对应刚体位置保持一致,并允许索过ALE索节点的物质流动,由约束代替接触,能够提高系统仿真计算的效率。为了能够模拟回收索在减速缓冲过程的应力传播反射和振动特性,将回收索在滑轮和挂钩接触位置的ALE索节点设为边界ALE索节点,在两个边界ALE索节点之间均匀布置若干个内部ALE索节点,约束内部ALE索节点的物质坐标与边界ALE索节点的物质坐标成比例的增长或缩短,由此保证减速缓冲过程中索变长度时系统的拓扑结构和自由度保持不变。基于ALE索描述的索式火箭回收着陆系统多体动力学模型是一个保拓扑的高效刚柔耦合多体动力学模型。

3.2 系统动力学分析

索式火箭回收着陆系统中的回收索和传递索采用相同材质的钢索,钢索的弹性模量为210 GPa,材料密度为7800 kg/m,截面半径为0.02 m和阻尼比为0.0001。利用上一节设计的液压减速缓冲装置凸轮外形曲线参数,对表1中的6种工况进行仿真计算。工况1为上一节的设计工况,在回收平面的中心捕获质量为5×10kg的火箭级段,液压减速缓冲装置的凸轮外形参数为式(24)和式(25),柱塞质量为=5×10kg,由式(23)确定储能器初始压强为0=869.37 kPa,其余的参数见文献[21]。工况2为着陆位置偏差(,)=(15 m, 15 m)处捕获质量为5×10kg的着陆火箭,液压减速缓冲装置的参数不变。其余4种工况为在中心位置分别捕获质量为3×10kg和7×10kg的着陆火箭,且液压减速缓冲装置中柱塞质量和储能器初始压强与工况1相同或根据对应回收火箭质量调整的情况。6种工况的着陆火箭着陆垂直速度均为30 m/s。

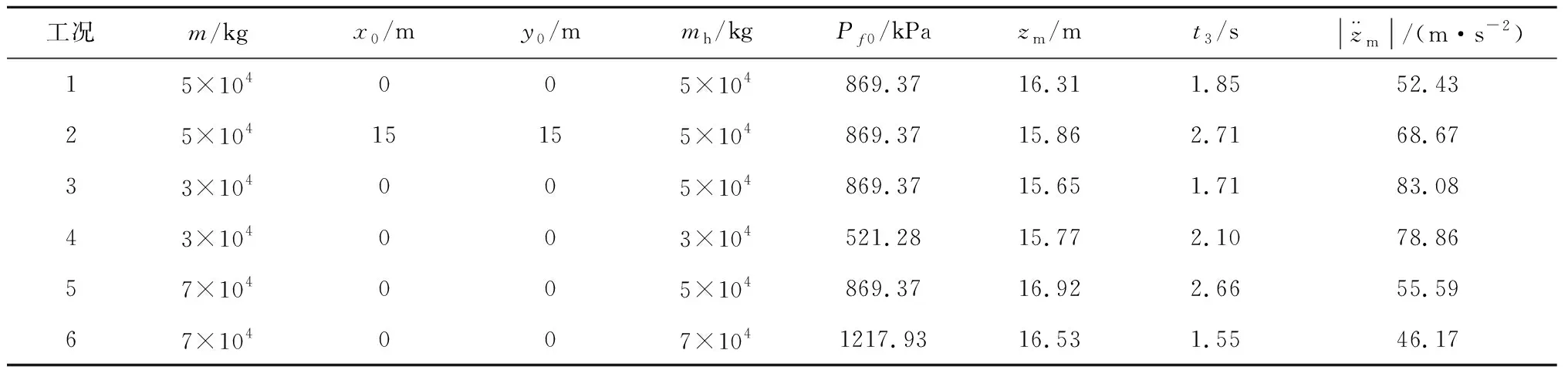
表1 仿真校验算例参数Table 1 Parameters of simulation verification cases

火箭减速缓冲过程的运动学特性目标值由式(1)和式(2)确定,理论值由MATLAB中采用四阶-五阶Runge-Kutta算法的求解器ode45计算式(8)获得,没有考虑索的柔性和质量的影响。工况1-6的仿真结果为基于系统的精准多体动力学模型,并利用清华大学多体动力学软件INSIDES向后差分积分器仿真计算获得。

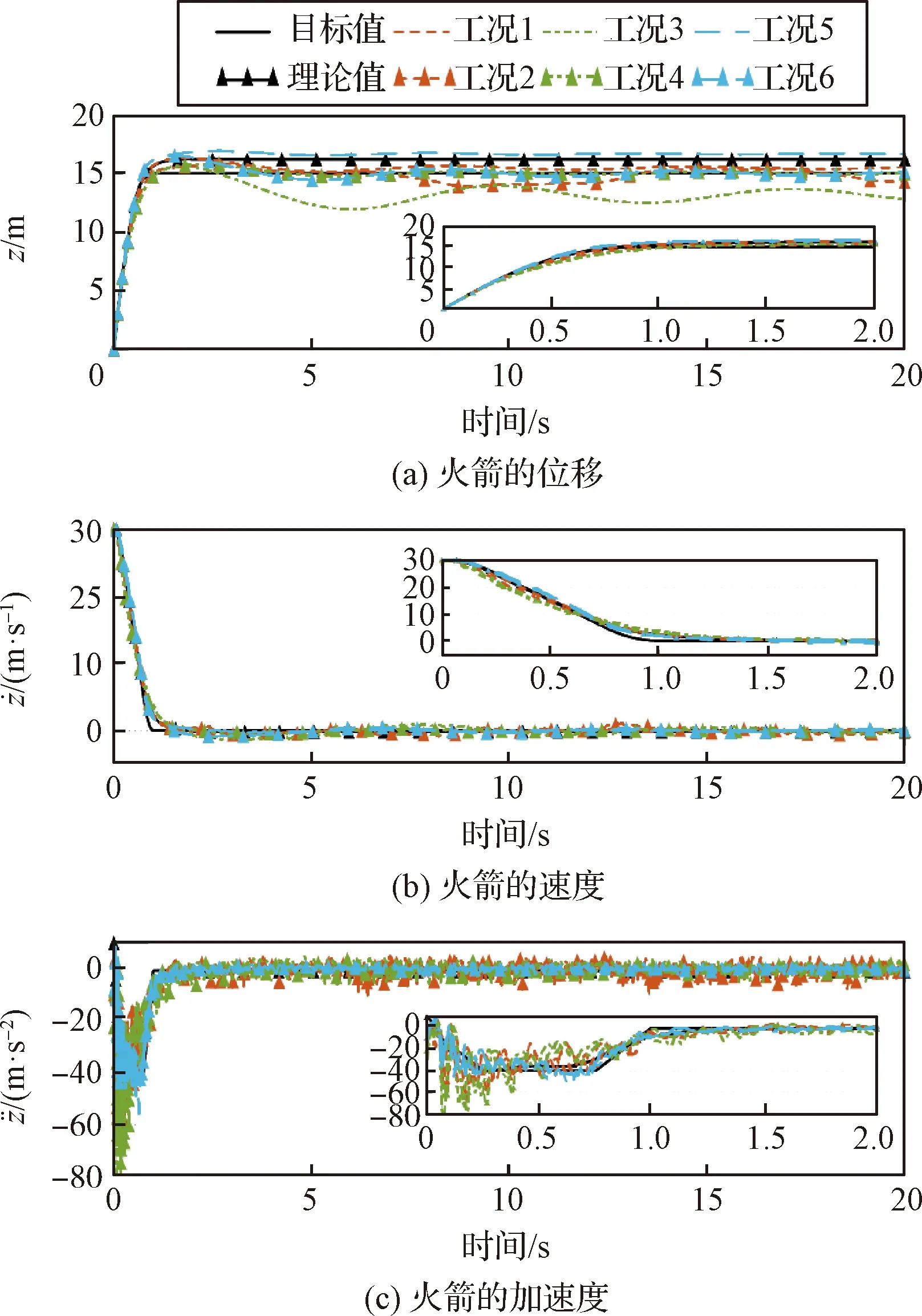
图10 火箭运动学特性Fig.10 Kinematic characteristics of the rocket

如图11所示,索的张力在减速缓冲的初始阶段剧烈的变动,这是由于索内的应力在火箭挂钩和滑块上的滑轮之间传播发生了反射叠加现象引起的。而索的张力变动随着时间增大而减弱,这是因为随着柱塞的滑移速度增大,液压阻尼的作用增大减弱了索的波动和振动。对比张力峰值可以看出,火箭的质量增大索的张力峰值明显增大。火箭在偏离中心位置着陆,工况2的索张力与工况1接近。系统减速缓冲不同质量的着陆火箭的索张力不同。针对相同质量的着陆火箭,更改液压减速缓冲装置配重和储能器初始体积对索张力的影响不大。

图11 回收索的张力Fig.11 Tension of the recovery cable

图12对比了不同工况的液压减速缓冲装置液压阻力,理论值和工况1的液压力仿真结果基本吻合。在初始阶段,6种工况的垂直速度相同,液压力相近,之后对不同的火箭质量液压减速缓冲装置产生不同的液压阻力。针对相同质量的着陆火箭,更改液压缓冲装置的柱塞配重和储能器初始体积对液压力的影响较小。火箭稳定时刻,液压阻尼力主要来源于储能器的压力,其大小也与火箭的质量相关。由此可以看出,当着陆火箭的质量大于或小于设计工况的着陆火箭质量,液压减速缓冲装置能够自动调整液压力使不同质量的着陆火箭减速稳定。与文献[21]相比,本文所设计的索式火箭回收着陆系统具有更大的缓冲能力,针对不同质量和着陆位置偏差的火箭具有自动调整液压阻力的能力。

图12 液压力Fig.12 Hydraulic pressure

4 结 论

本文提出了一种用于索式火箭回收着陆系统的地面液压缓冲装置,用来提高对着陆火箭的减速缓冲能力和实现对不同着陆质量和着陆位置的着陆火箭的自动调整液压阻力的能力。针对特定的火箭减速缓冲运动学特性,基于最小二乘法和系统的动力学特性对凸轮外形进行反问题设计,并建立系统的多体动力学模型进行仿真校验。仿真结果表明：系统能够对质量为5×10kg和垂直着陆速度为30 m/s的着陆火箭进行减速缓冲,并且能够针对不同质量和着陆位置的火箭自动调节液压阻力,火箭的减速缓冲运动学特性符合所提反问题设计方法的目标值。本文所提索式火箭回收着陆系统具有较强的减速缓冲能力和自动调整减速缓冲液压阻力的能力,适用于未来大型火箭和未知质量的火箭回收着陆减速缓冲。