神经网络修正的速度约束辅助车载SINS定位算法
李正帅,缪玲娟,周志强,吴子昊
(北京理工大学自动化学院,北京 100081)
0 引 言
车载全球导航卫星系统(GNSS)/捷联惯性导航系统(SINS)组合导航系统中的GNSS信号不可用时,仅使用SINS导航定位精度逐渐下降,难以满足要求。速度约束辅助SINS定位假设车辆在行驶过程中没有发生侧滑和跳跃,利用车辆横向和竖向速度为零的约束条件修正SINS的误差,可以在不增加成本的前提下,提高定位精度。付强文等利用速度约束辅助SINS定位,将其作为里程计失效的备选方案,定位精度优于仅使用SINS定位。为了进一步提高速度约束辅助SINS的定位精度,胡杰等在速度约束辅助SINS的基础上,引入模糊推理系统自适应调节量测噪声方差阵,通过试验验证了速度约束和自适应滤波对于提高SINS位置精度的有效性。
车辆长时间朝某一固定方向行驶时,使用速度约束辅助SINS其纵向位置误差会逐渐累积增大。韩勇强等结合高阶曲线拟合的方法对车辆纵(前)向速度残差导致的定位误差进行补偿,能够有效弥补仅使用速度约束的不足,但是该算法需要停车观测纵向速度残差才能对纵向位置误差进行补偿,不能在连续行驶过程中在线修正,这对于一般情况下不能随意停车的城市隧道场景具有一定的局限性。陈映秋等将微机电系统(Micro-elector-mechanical system, MEMS)惯性测量单元(Inertial measurement unit, IMU)安装在载体车轮中心,提取出纵向速度信息,相比于仅使用速度约束增加了一维纵向速度约束,提高了自主导航性能,但是考虑到实际载车安装和布线等因素该方案不易实现。李博文等将车辆瞬时运动看作不同曲率半径的圆周运动,根据纵向速度、竖向角速度和比力测量值构造向心加速度差值误差作为新量测量,将其与速度约束一同辅助车载SINS定位,新量测量提高了横向加速度计偏值的可观测性,理论上会因此提高定位精度,但是引入的新量测量中的比力没有考虑杆臂加速度补偿,杆臂加速度误差等效为加速度计测量误差,动态情况下角加速度通过角速度微分得到,会引入较大噪声,对杆臂加速度难以实现精确补偿。
随着人工智能技术的发展,大量专家学者将神经网络算法用于预测修正导航误差。目前常用的神经网络算法有卷积神经网络(Convolutional neural networks, CNN)、BP(Back propagation)神经网络、径向基函数(Radial basis function,RBF)神经网络等。CNN主要用于识别位移、缩放及其他形式扭曲不变的二维图形,在图像识别、图像分类等领域应用广泛;BP神经网络是一种全局逼近网络,结构简单且适用于非线性函数逼近,但是易陷入局部极小值,学习速度较慢,对于对实时性要求高的应用场景具有一定的局限性;RBF神经网络是一种局部逼近网络,相较于全局逼近网络(如BP神经网络),局部逼近可以简化计算量,并且它只有一个隐含层,因此RBF神经网络的训练速度更快,能够满足对实时性有要求的应用场景。RBF神经网络的突出优点是具有很强的非线性映射能力和很快的学习收敛速度。研究表明,RBF神经网络是连续函数的最佳逼近。
为了提高GNSS失效时车载SINS的导航精度,本文在不增加额外传感器的情况下利用速度约束辅助SINS定位,提出一种限定记忆指数加权的自适应滤波算法,实时估计量测噪声,以提高滤波器对新近量测数据的利用权重以及对外界环境的适应能力;在此基础上,针对车辆长时间朝某一固定方向行驶时仅使用速度约束辅助SINS其纵向位置误差发散较严重的问题,提出一种基于神经网络的纵向位置误差修正算法,引入RBF神经网络算法在线预测纵向位置误差修正系数,对定位结果进一步修正。在人为设置GNSS失效和真实隧道场景下进行车载试验,验证了本文算法的有效性与可行性。
1 车载GNSS/SINS组合导航系统数学模型
1.1 状态方程
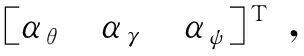

(1)

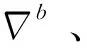
=
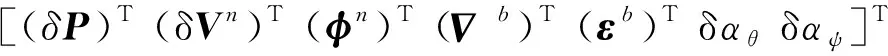
(2)
滤波器状态方程为:

(3)
式中:为SINS误差方程和安装误差角误差方程构造的状态转移矩阵;为系统噪声输入矩阵;为系统噪声。
1.2 量测方程
GNSS有效时,将SINS解算的位置、速度信息与GNSS输出的位置、速度信息分别求差作为滤波器量测值,此时量测方程为:
=+
(4)
式中:表示量测量;表示量测噪声;表示量测矩阵,表达式为:

(5)
GNSS失效时,采用速度约束构造量测方程。车体坐标系系下速度分量为:

(6)
根据速度约束构成量测量:

(7)

对式(6)进行全微分,并考虑式(1)则有:


(8)
式中:δ表示系下速度误差;[()]表示取的反对称矩阵。
由式(7)和式(8)可得量测方程:
=+
(9)
式中:为量测矩阵。
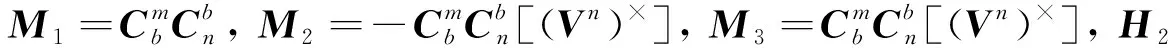
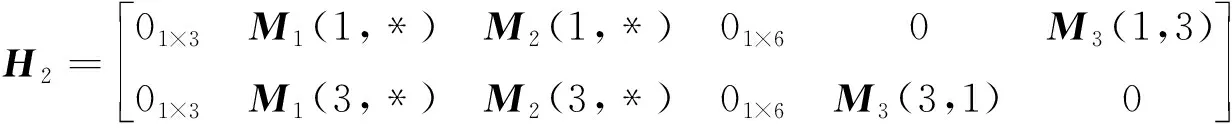
(10)
式中:(1,*)表示取的第1行,其余符号含义类似;表示量测噪声。
2 限定记忆指数加权的自适应滤波算法
标准卡尔曼滤波要求系统的数学模型、系统噪声和量测噪声统计特性准确已知。但是在实际工程应用中,量测噪声受外界环境因素影响,具有较大的不确定性,卡尔曼滤波器使用不准确的量测噪声统计特性会产生较大的状态估计误差,甚至可能使滤波发散。本文对量测噪声协方差阵进行自适应调整。
理想情况下滤波残差满足零均值高斯白噪声分布的条件,其理论协方差为:

(11)
一般根据区间长度为的滤波残差序列对进行极大似然最优估计,对滑动窗口内的数据求取算术平均。为了提高滤波残差协方差的估计精度和滤波器对新近量测数据的利用权重,本文对滑动窗口内的数据进行指数加权。
时刻的滤波残差协方差的估计值为:

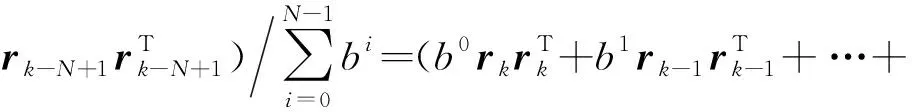
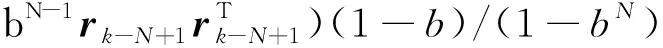
(12)
式中:为窗口大小;为指数因子,0<<1。历史时刻的残差数据离当前时刻越远,在求残差协方差的估计值时所占比重越小。
根据文献[13]中极大似然法的证明方法,可以证明本文算法提出的式(12)仍是的极大似然最优估计。
为了减小计算量和存储空间,对式(12)进一步化简,得到递推公式:
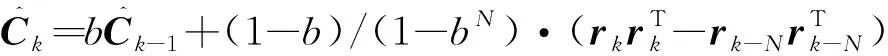
(13)
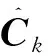


(14)
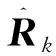

(15)
3 基于神经网络的SINS纵向位置误差修正算法
RBF神经网络是一种三层前馈网络模型,由输入层、隐含层和输出层组成。从输入层到隐含层的变换是非线性的,从隐含层到输出层的变换是线性的。网络的参数主要有三种:径向基函数的中心、方差和隐含层到输出层的权值,对网络的训练过程即为求解这三种参数的过程。
假设城市环境中GNSS有效时的训练样本包括了车辆多种机动状态下的数据,通过GNSS有效场景下的样本数据训练神经网络,利用神经网络的预测功能估计GNSS失效场景下SINS纵向位置误差的修正系数。
车辆的运动状态可由速度和姿态描述,其中姿态可由四元数表示。由于该四元数为规范化四元数,所以可以选取四元数的3个虚部作为神经网络输入量的一部分,从而减小计算量。对于神经网络的训练样本,本文选取GNSS有效时SINS解算的3个速度、3个四元数虚部共6个量作为神经网络的输入量,输出量为修正系数∘表示使用速度约束辅助SINS定位滤波周期内,纵向行驶的距离修正后与修正前的比值;通过在GNSS有效时的滤波周期内进行GNSS/SINS组合导航的同时,并行使用速度约束辅助SINS定位来求取。
输出量求解过程中车辆的位置示意图如图1所示。
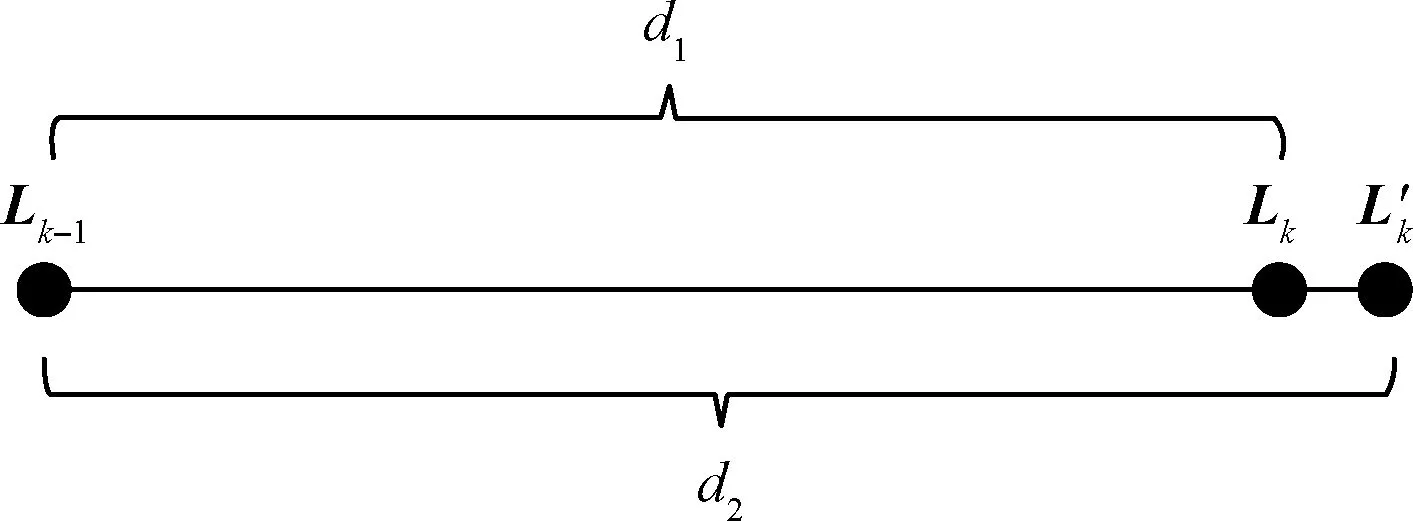
图1 输出量s求解过程中车辆的位置示意图Fig.1 Schematic diagram of vehicle position in the process of output s solution
图1中,-1与分别表示-1时刻与时刻GNSS/SINS组合导航定位的车辆位置;′表示GNSS有效时使用速度约束辅助SINS定位的车辆位置;表示-1与间的距离;表示-1与′间的距离。的大小为:

(16)
在GNSS有效时输出的导航结果为GNSS/SINS组合导航的位置,速度约束辅助SINS定位的位置仅用于计算和。
当GNSS有效时记录样本数据(6个输入量,1个输出量),在GNSS失效时的第一时刻利用GNSS失效前记录的最新的组样本数据进行训练。可设置为500或适当调整。训练过程包括读取样本数据、初始化神经网络、训练神经网络、存储网络参数。
在GNSS失效的后续时间里,读取网络参数,以当前时刻惯导解算的3个速度、3个四元数虚部作为输入量,预测修正系数′,′表示神经网络预测的SINS纵向位置误差修正系数。
时刻神经网络修正位置示意图如图2所示。

图2 位置修正示意图Fig.2 Schematic diagram of position correction
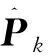
时刻经过神经网络修正后的车辆纬度、经度分别为:

(17)
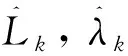
本文算法流程图如图3所示,实现步骤如下:

图3 本文算法流程图Fig.3 Flow chart of the proposed algorithm
1)首先建立状态方程,当GNSS有效时,进行GNSS/SINS组合导航,并存储用于RBF神经网络训练的样本数据。
2)当GNSS失效时,采用速度约束和自适应滤波辅助SINS,在GNSS失效的第一时刻对神经网络进行初始化,通过已存储的样本数据对神经网络进行训练,并存储网络参数。
3)在GNSS失效的后续时间里,将SINS解算的速度、四元数信息作为神经网络的输入量预测纵向位置误差修正系数′。
4)根据式(17)对速度约束辅助SINS定位后的位置进行修正。
4 试验结果与分析
基于所设计的神经网络修正的速度约束辅助车载SINS定位算法,在人为设置GNSS失效和真实隧道场景下进行了车载试验,对采集的原始MEMS惯导数据和GNSS数据进行离线仿真,验证了算法的有效性与可用性。
4.1 试验条件
车载试验通过LaneTo-3低成本GNSS/MEMS SINS组合导航设备实现对MEMS惯导数据和卫星数据的采集。测试的同时搭载Mars-D高精度GNSS/SINS组合导航定位系统,该系统采用紧组合的方式将惯导与双天线差分GNSS定位进行组合,开放天空下定位精度可至厘米级;结合地图数据库信息和反向平滑技术,卫星信号中断120 s位置精度(1)小于1 m。将Mars-D处理后的导航结果作为基准用于统计本文算法的误差。
车载试验系统如图4~6所示。

图4 天线安装位置Fig.4 Position of antenna installation

图5 LaneTo-3组合导航设备Fig.5 LaneTo-3 integrated navigation device

图6 Mars-D高精度组合导航定位系统Fig.6 Mars-D high precision integrated navigation positioning system
用于采集试验数据的LaneTo-3组合导航设备中陀螺仪和加速度计的基本参数如表1所示。

表1 陀螺仪和加速度计基本参数Table 1 Basic parameters of the gyroscope and accelerometer
试验场景主要测试直线行驶和隧道情况。试验路线如图7~9所示,选取路段1~3:
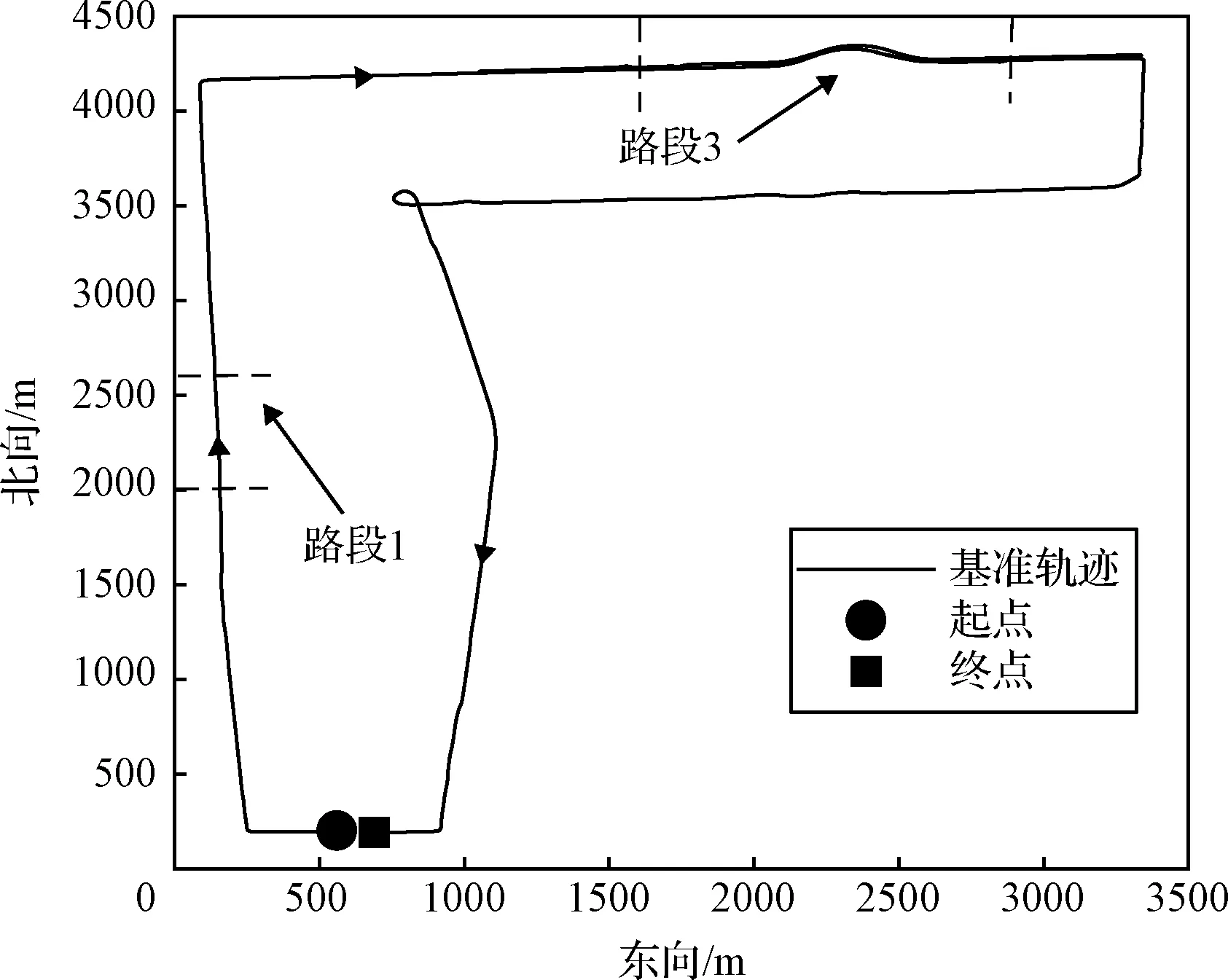
图7 路段1与路段3车辆轨迹Fig.7 Vehicle tracks on Route 1 and Route 3

图8 路段2车辆轨迹Fig.8 Vehicle track on Route 2

图9 路段3车辆轨迹Fig.9 Vehicle track on Route 3
1)路段1如图7所示,选在北京市牡丹园站所在的南北直线路段,将GNSS数据断开60 s,模拟直线隧道场景,卫星断开时间内载车直线行驶约600 m,车辆先加速再减速,速度范围是14.4~50.4 km/h。
2)路段2如图8所示,选在北京市北四环中路的东西直线路段,将GNSS数据断开60 s,模拟直线隧道场景,卫星断开时间内载车直线行驶约1020 m,车辆先加速再减速,再加速,速度范围是47.5~70.6 km/h。由于车辆长时间朝某一固定方向行驶时使用速度约束辅助SINS其纵向位置误差发散较严重,因此路段1和路段2用于测试本文算法在直线路段的性能。
3)路段3如图7、图9所示,选在北京市慧忠路隧道附近,该隧道卫星失效路段单向全长约1.2 km,由小角度弧形弯道和直线路段组成,用于测试本文算法在真实隧道场景下的整体性能。行驶轨迹为自西向东进入隧道,调头自东向西第二次进入隧道后再次调头自西向东进入隧道,即进入隧道共三次。车辆机动主要是航向转弯和直线行驶等动作,车速约45 km/h。
图7~9中两条虚线中间的路段为卫星失效路段,箭头表示行驶方向,图9中的序号表示箭头的先后次序。
4.2 算法校验
本文算法使用提出的限定记忆指数加权的自适应滤波实现速度约束辅助SINS定位,并通过RBF神经网络预测系数对滤波后的位置进一步修正。
为了检验本文算法中提出的自适应滤波算法及神经网络修正的效果,将使用标准卡尔曼滤波的速度约束辅助SINS的算法(简记为“KF-VC”)、只使用本文提出的自适应滤波的速度约束辅助SINS算法(简记为“AKF-VC”)与完整的本文算法(简记为“RBF-AKF-VC”)进行了对比。
KF-VC算法、AKF-VC算法与RBF-AKF-VC在处理三个路段的试验数据后的位置误差、速度误差对比如图10~15所示,三个路段均为GNSS失效路段。

图10 路段1位置误差对比Fig.10 Comparison of position errors on Route 1
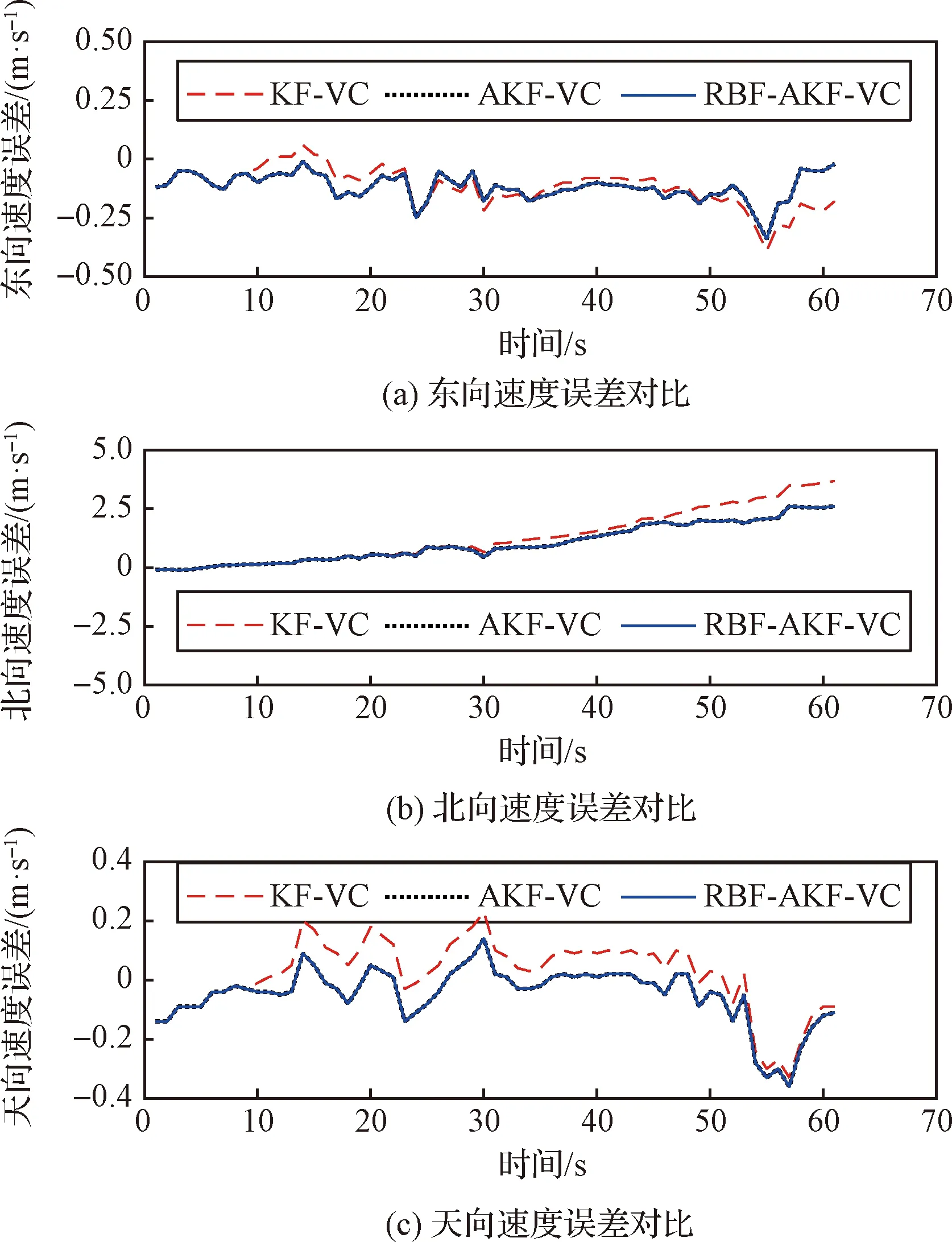
图11 路段1速度误差对比Fig.11 Comparison of velocity errors on Route 1

图12 路段2位置误差对比Fig.12 Comparison of position errors on Route 2
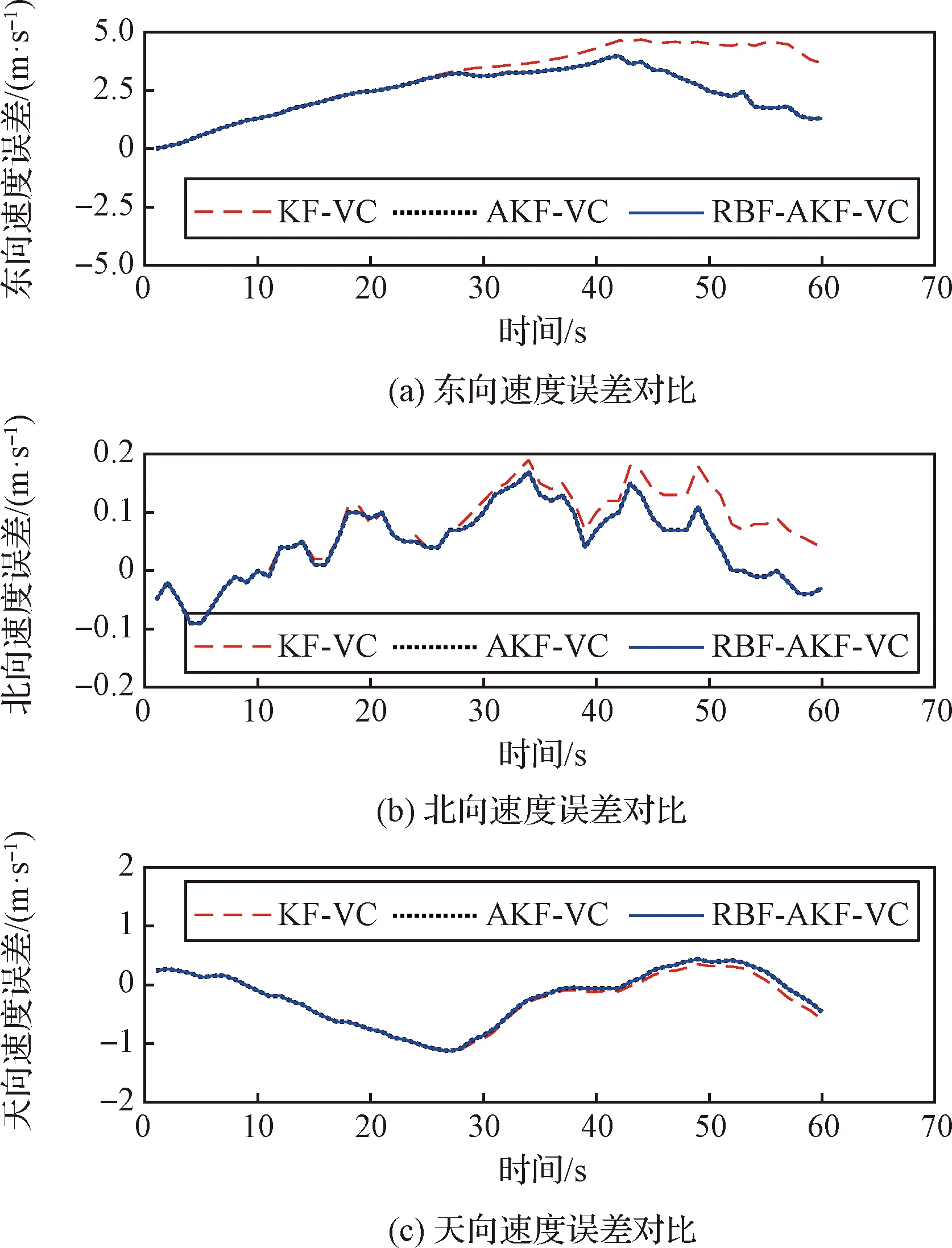
图13 路段2速度误差对比Fig.13 Comparison of velocity errors on Route 2
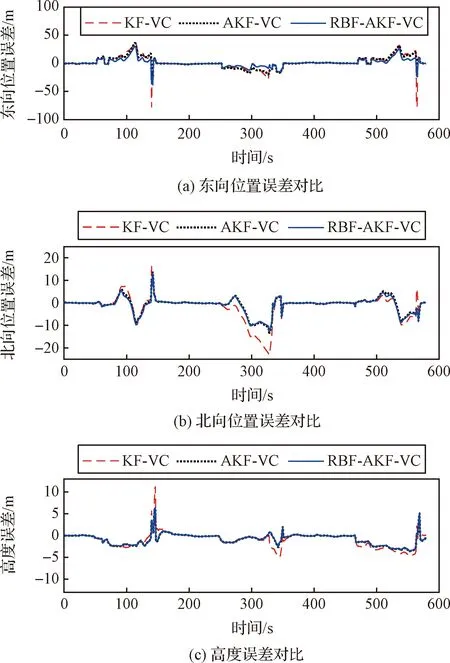
图14 路段3位置误差对比Fig.14 Comparison of position errors on Route 3
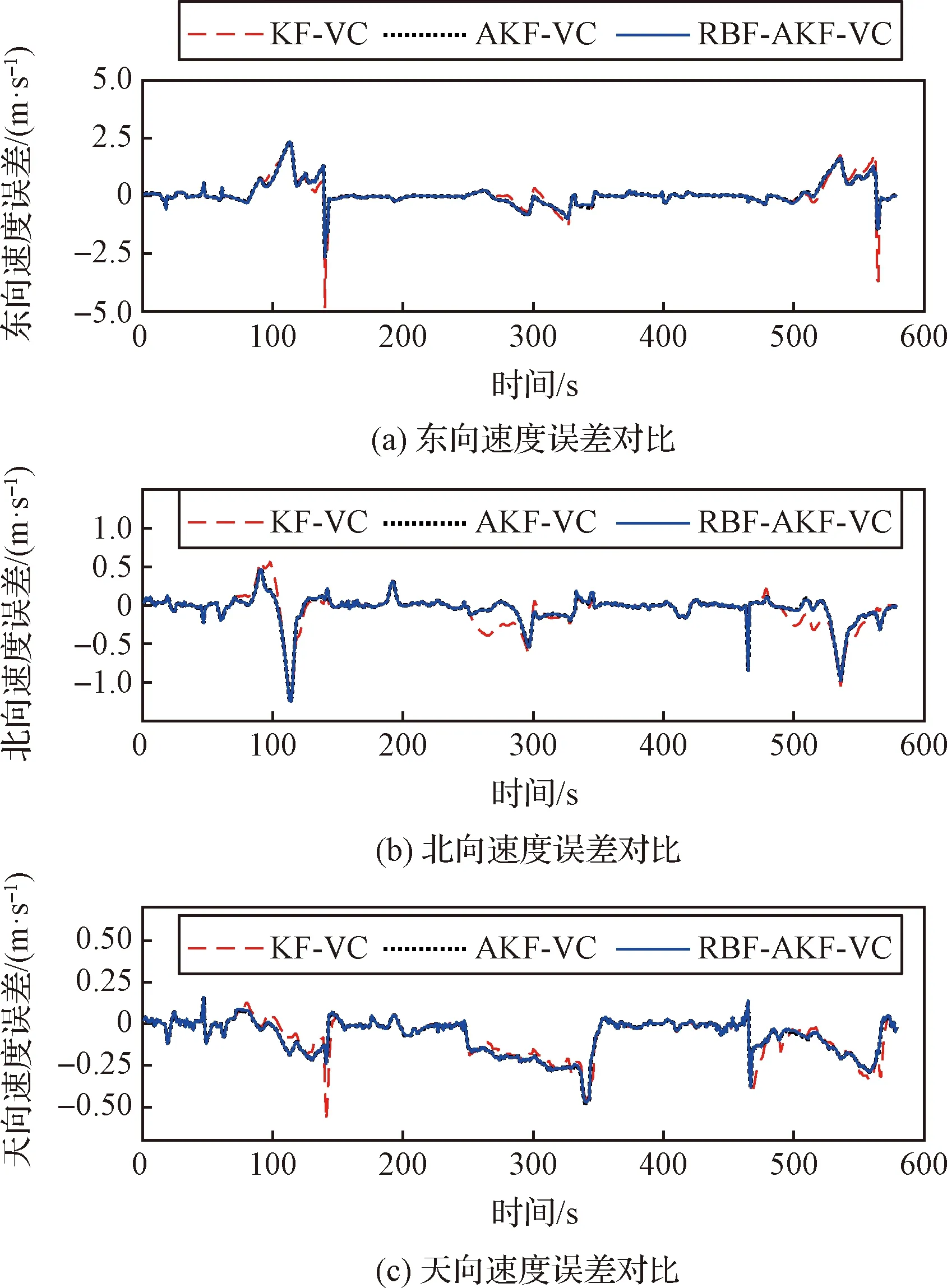
图15 路段3速度误差对比Fig.15 Comparison of velocity errors on Route 3
图10~15中实线表示RBF-AKF-VC算法处理试验数据后的位置误差、速度误差,虚线、点线分别为KF-VC算法、AKF-VC算法对应的误差曲线。从图10~15中可以看出,对于GNSS失效的场景,RBF-AKF-VC算法的导航精度最高;AKF-VC算法相对于KF-VC算法,位置误差与速度误差均减小;从图10、图12和图14可以看出,利用神经网络修正位置误差,能够进一步提高SINS的位置精度。
为了定量表示本文算法中提出的自适应滤波算法与神经网络修正的效果,分别统计KF-VC算法、AKF-VC算法与RBF-AKF-VC算法在三个路段上的均方根误差(RMSE),路段3先、后三次进入隧道依次统计。结果如表2~表4所示。

表2 路段1三种算法的均方根误差对比Table 2 RMSE comparison of the three algorithms of Route 1

表3 路段2三种算法的均方根误差对比Table 3 RMSE comparison of the three algorithms of Route 2
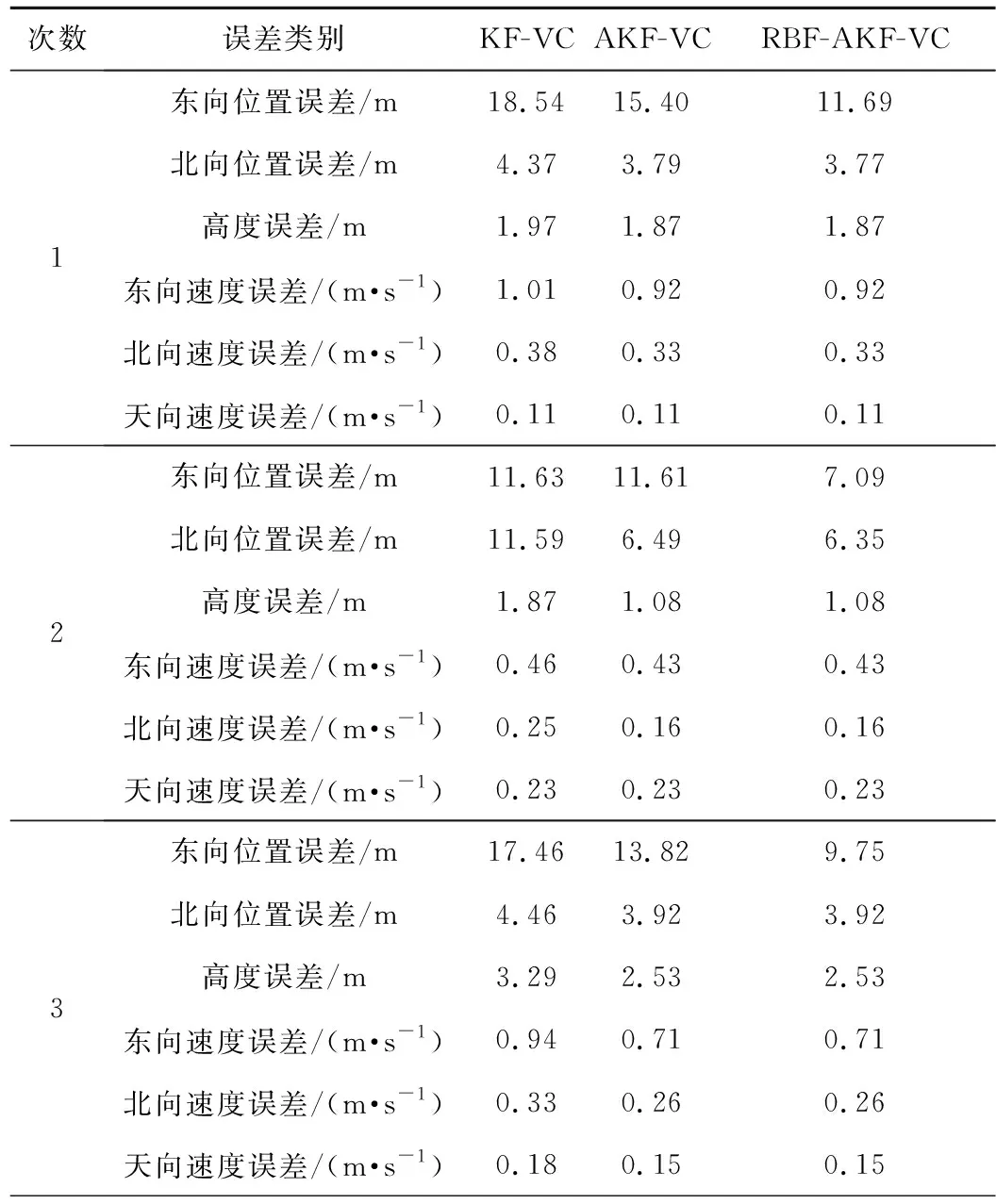
表4 路段3隧道场景三种算法的均方根误差对比Table 4 RMSE comparison of the three algorithms in tunnel scene of route 3
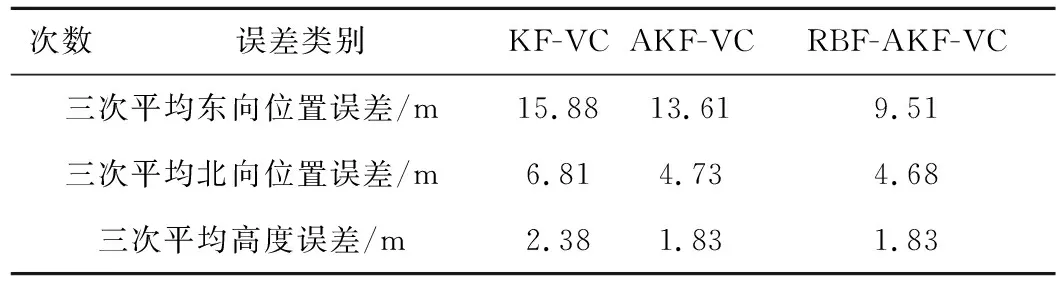
续表4
由表2、表3可知,由于路段1主要是南北向直线行驶路段,路段2主要是东西向直线行驶路段,缺少转弯机动过程,仅有横向和竖向的速度约束,纵向速度误差逐渐增大。表2中,北向速度误差明显大于东向速度误差,导致路段1的北向位置误差明显比东向位置误差大;而表3中,东向速度误差明显大于北向速度误差,进而导致路段2的东向位置误差明显比北向位置误差大。相比于KF-VC算法,RBF-AKF-VC算法在路段1上的东向位置误差减小了35.66%,北向位置误差减小了74.20%,高度误差减小了7.34%,三个方向的速度误差均减小,北向速度误差减小得最多(减小了0.42 m/s);在路段2上的东向位置误差减小了59.14%,北向位置误差减小了66.47%,高度误差减小了15.21%,三个方向的速度误差均减小,东向速度误差减小得最多(减小了0.81 m/s)。AKF-VC算法提高了滤波器对新近量测数据的利用权重与滤波精度,使定位精度得到了一定的提升;RBF-AKF-VC算法使用神经网络预测系数修正了SINS纵向位置误差,相比于AKF-VC算法,在路段1上东向位置误差进一步减小了16.27%,北向位置误差进一步减小了61.96%;在路段2上东向位置误差进一步减小了43.21%,北向位置误差进一步减小了46.15%。
表4中三次的试验结果中,相对于北向位置误差,东向位置误差较大,这是由于车辆在路段3上的整体行驶轨迹是东西方向的,采用速度约束缺少对纵向速度的量测更新,长时间在一个方向行驶该方向位置误差会逐渐积累。其中第2次的行驶方向与第1、3次相反,转弯方向也相反。相比于KF-VC算法,RBF-AKF-VC算法在路段3先、后三次往返进入隧道的车辆定位精度均得到了提高,东向位置误差平均减小了40.11%,北向位置误差平均减小了31.28%,高度误差平均减小了23.11%,三个方向的速度误差均减小,东向速度误差减小得最多(平均减小了0.12 m/s)。RBF-AKF-VC算法使用神经网络预测修正系数对SINS纵向位置误差进行修正后,相比于AKF-VC算法,位置误差可进一步减小,尤其是东向位置误差减小了30.35%。
5 结 论
车载GNSS/SINS组合导航在GNSS失效SINS单独工作时误差会逐渐增大,本文在不增加额外传感器的前提下利用速度约束辅助SINS定位。提出一种限定记忆指数加权的自适应滤波算法实时估计量测噪声,提高了滤波器的适应能力;与此同时,针对仅使用速度约束辅助SINS其纵向位置误差会逐渐发散的问题,提出一种基于RBF神经网络的纵向位置误差修正算法,通过神经网络训练预测系数进一步修正滤波后的定位结果。在人为设置GNSS失效和真实隧道场景下进行车载试验,结果表明,本文算法对于位置误差的修正效果优于标准卡尔曼滤波和速度约束辅助SINS相结合的常规算法,具有较高的定位精度;其中RBF神经网络预测的修正系数对于纵向位置误差具有较好的修正效果,为解决速度约束辅助SINS定位其纵向位置误差发散的问题提供了一种新思路和新方法。本文算法不增加硬件成本,对提高低成本车载导航在卫星信号丢失时的定位精度具有重要意义。

