目标加速度未知下的导弹自适应滑模拦截制导
梁小辉,贾坤浩,田煜辉,许 斌
(西北工业大学自动化学院,西安 710129)
0 引 言
随着当代军事武器的快速发展,为了保障国家安全,导弹作为空间防御的尖端武器,得到了重点攻关与研究。制导系统作为导弹武器的核心,直接影响着空间拦截任务的成功与否。但是,随着航空航天技术的不断发展,拦截目标的速度越来越高、机动性越来越强、干扰措施越来越多,传统导引方法难以满足现代战争的反导拦截要求,因而想要更好地发挥导弹拦截性能,就需考虑设计具有更高精度和适应性的制导控制方法。
比例导引作为一种典型的传统制导方式,其主要思想是:整个制导过程中,导弹速度矢量的转动角速度与弹-目连线的旋转角速度成特定比例。文献[2]在传统比例制导的基础上引入了碰撞角约束,整个制导控制律由比例导引和碰撞角偏差控制项组成,目的是使碰撞角偏差在终点时刻收敛至极小值。文献[3]设计了一种基于DDPG算法的末制导方法,通过对拦截环境状态和动作(控制量)进行设计,实现了从仿真环境交互数据中学习回报最优的制导律。文献[4]针对常用比例导弹导引律制导命中率低的问题,分析了比例导引律、偏置比例导引律、修正比例导引律的制导性能,提出了一种基于扩展比例导引律的制导模型。因为其简单、易于实现的特点,比例导引方法得到了广泛应用,但是针对大机动目标、速度/加速度信息难以捕获等情况,其制导效果将大打折扣甚至脱靶。
为了提高导弹制导系统的鲁棒性能,滑模变结构控制被广泛应用于导弹武器系统的制导设计中。针对空-空导弹的目标拦截问题,文献[6]在比例导引的基础上设计了一种变结构制导控制方法。文献[7]针对传统制导和控制分开设计在拦截高速机动目标时的缺陷,设计了一种自适应最优滑模制导与控制一体化算法。文献[8]利用积分滑模和自适应控制技术,保证了多颗导弹能够在有限时间内同时拦截机动目标。针对不机动目标,文献[9]利用自适应时变滑模控制技术设计了一种带碰撞角约束的拦截制导律。针对具有加速度机动的目标拦截问题,文献[10]提出了一种时变全局滑模制导控制方法,通过线性扩张状态观测器估计了目标的加速度,设计了一种带攻击角约束的制导控制方法。考虑导弹自动驾驶仪的动态特性,结合滑模控制理论,文献[11]研究了反临近空间高超声速目标拦截导弹的制导律及滤波器设计问题,完成了临近空间拦截导弹的制导律辨识和飞行轨迹预报。文献[12]提出一种基于滑模理论的导弹制导方法,在设计趋近律时考虑到弹-目距离的变化,使得系统状态轨迹快速收敛到滑模面,并通过饱和函数替代符号函数抑制了状态轨迹在到达滑模面时的抖动。文献[13]利用Hopfield神经网络在线实时求解最优制导问题,克服了实际中最优制导难于求解的问题。文献[14]基于抑制弹目视线旋转的原则,设计了一种视线转率收敛速率可调的跟踪剖面,选取跟踪误差与其积分为状态变量,基于有限时间收敛的积分滑模面与快速趋近律推导得到了积分滑模制导律。文献[15]在弹-目运动方程存在参数不确定性情况下,提出一种基于自适应PID滑模扰动观测器技术的鲁棒最优末制导律。文献[16]针对攻击角度存在约束的拦截制导问题,提出了一种基于RBF神经网络的带末端角约束的滑模制导律。虽然导弹拦截制导已经取得了很大的成就,但是由于实际飞行环境复杂,导弹制导控制系统会受到外界未知扰动的影响,特别是随着拦截目标机动方式多样化、机动能力的增强,导引头无法精确获得机动信息,因而有必要研究能准确对目标机动信息进行在线估计、具有鲁棒性的末制导方法。
基于上述分析讨论,本文设计了一种基于RBF神经网络的自适应滑模制导控制设计方法,有效提高了导弹拦截制导算法的自适应能力。首先,给出了弹-目三维运动关系,构建了面向制导设计的运动模型;然后,利用RBF神经网络的任意逼近能力,估计了目标加速度信息,并在此基础上设计了自适应滑模制导律;同时利用连续高增益法削减了滑模抖振影响,结合零化视线角的设计思想,证明了所提方法的收敛性;最后,通过三种不同拦截场景下的仿真试验,验证了所提滑模制导律对目标机动有较高的自适应性和鲁棒性。
1 弹-目模型与问题描述
1.1 弹-目模型
在三维空间中,构建导弹-拦截目标的运动模型,如图1所示,其中,-和-分别表示地面坐标系和视线坐标系,∈为弹-目相对加速度,∈为弹-目相对速度,∈弹-目相对位置,∈表示坐标系-相对于坐标系-的角速度,为向量扩张成的斜对角矩阵。根据弹-目运动学关系有,
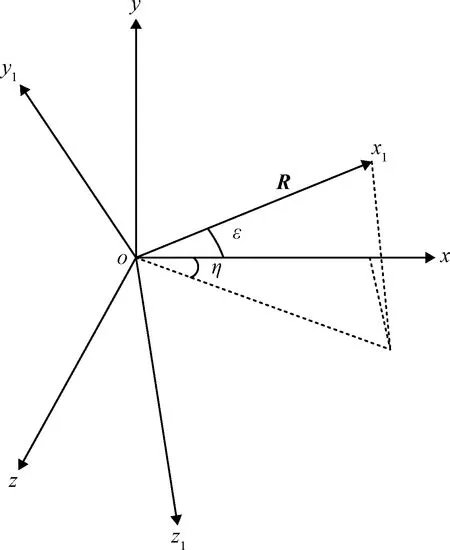
图1 三维拦截示意图Fig.1 Three-dimensional interception

(1)


(2)


(3)
整理上式可得:
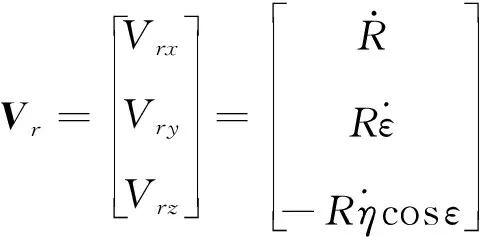
(4)
根据式(1)、(3)和(5)可知,
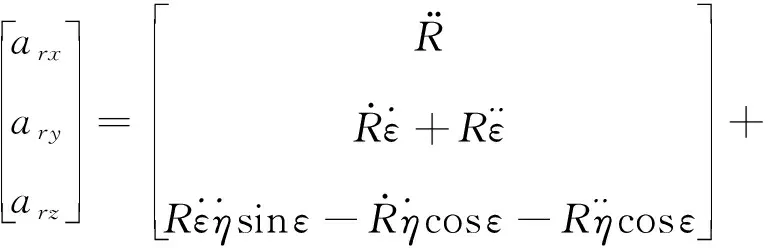
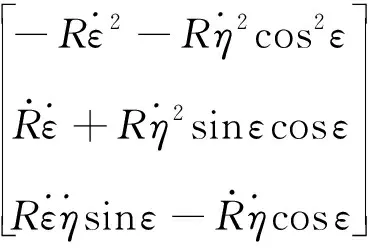
(5)
整理上式可得:
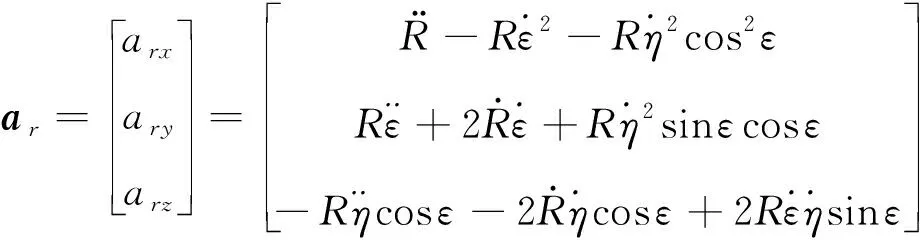
(6)
定义=[],=[]分别表示导弹和拦截目标的加速度,此时弹-目相对运动模型可表示为

(7)
1.2 问题描述
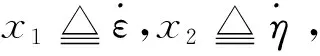

(8)

(9)
式(8)和(9)分别表示视线角在俯仰平面和偏航平面的角速率变化动态,即式(7)构建的导弹三维运动被转化为两个二维平面的制导控制问题。根据导弹拦截的实际情况,一般导弹速度大于目标速度,只对导弹俯仰和偏航平面的运动方向进行控制,通过零化视线角速率的方式来实现最终的制导拦截,即实现→0和→0。
综上所述,本文的主要目的是:针对式(7)构建弹-目三维相对运动模型,在拦截目标加速度未知的情况下,基于RBF神经网络对其估计补偿,设计权重自适应律;基于零化视线角速率的设计思路,构建俯仰平面和偏航平面的滑模制导律,使得导弹可以高精度瞄准目标,完成目标拦截任务,提高了导弹的整体拦截性能。
2 基于自适应神经网络的滑模制导律设计
本节针对导弹俯仰平面和偏航平面的弹-目运动关系,分别设计了对应的神经自适应滑模制导律,其结构框图如图2所示。在制导控制律设计中,充分考虑目标加速度不能精确获得的实际情况,将目标加速度视作制导系统的外部干扰,基于RBF神经网络对其进行估计补偿,在此基础上设计了自适应滑模制导律,保证了方位视线角和高低视线角收敛到零。
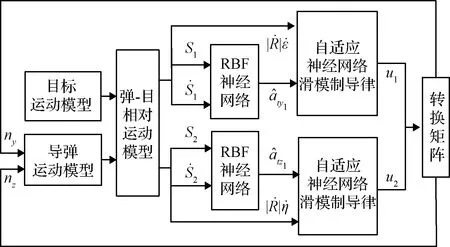
图2 基于RBF神经网络的滑模制导律框图Fig.2 Block diagram of the sliding mode guidance law based on RBF neural network
利用RBF神经网络的任意逼近能力估计目标加速度信息,此时将目标的未知加速度视为制导系统的未知有界扰动,令()=,()=,则弹-目运动关系式(8)~(9)可改写为:
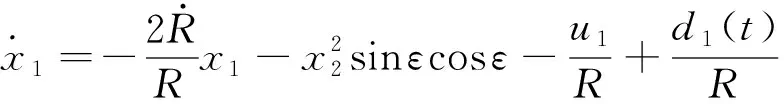
(10)
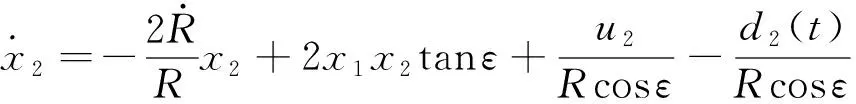
(11)
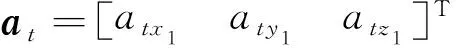
根据零化弹-目视线角速率的制导设计理念,结合滑模控制理论,对式(10)和(11)设计下述的滑模面:
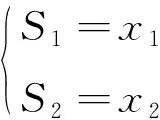
(12)
利用RBF网络去估计()和(),则有:
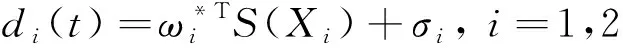
(13)
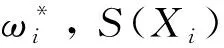

(14)
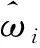
权重估计误差为
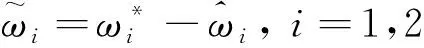
(15)
2.1 俯仰平面制导律设计
针对式(10)所示的俯仰平面弹-目运动关系,设计如下所示的制导律和权重更新律,


(16)
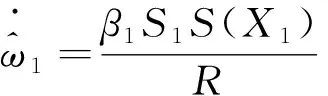
(17)
式中:>0,>0为消除俯仰平面系统不确定性的增益系数。

. 构造如下所示的Lyapunov候选函数

(18)
对式(18)求导可得
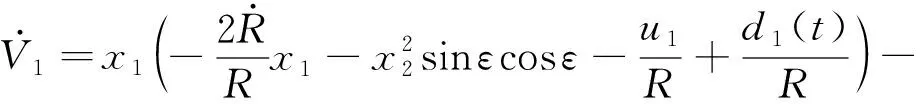
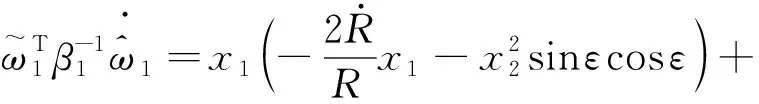
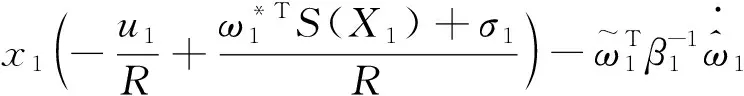
(19)
将式(16)~(17)代入式(19)可得,


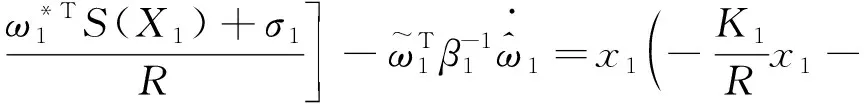
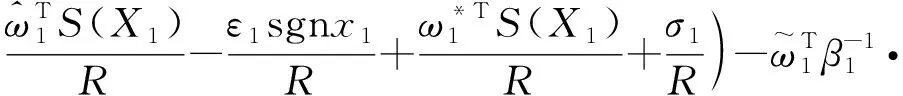
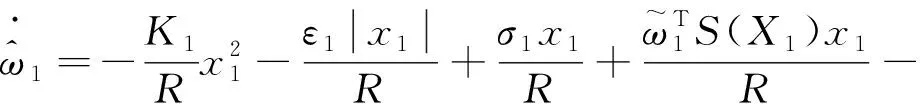
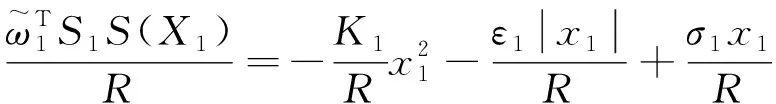
(20)
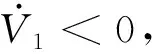
式(19)~(20)分母中含有的弹-目相对距离,在实际应用中,当制导精度达到要求,对进行固化处理以避免自适应参数增速过大的问题。
2.2 偏航平面制导律设计
针对式(11)所示的偏航平面弹-目运动关系,设计如下所示的制导律和权重更新律,
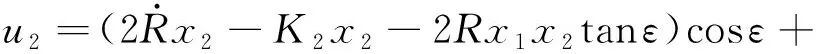

(21)

(22)
式中:控制参数和均大于零,此时可得到如下所示的定理。
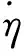
构造下述的Lyapunov候选函数
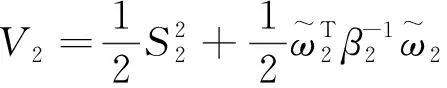
(23)
对上式求导有
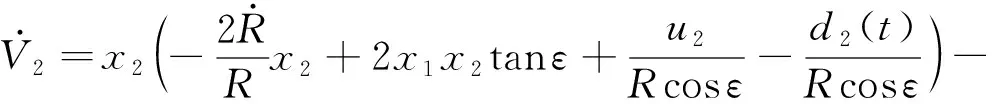
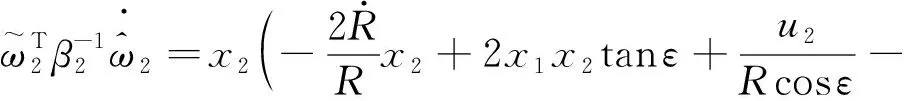
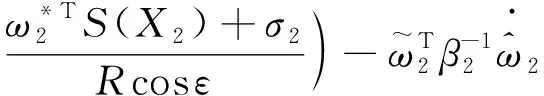
(24)
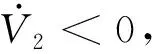
将式(21)~(22)代入上式可得,

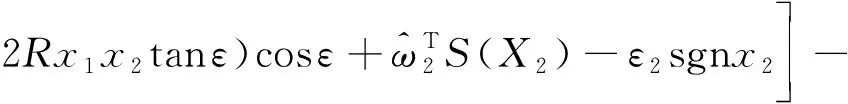
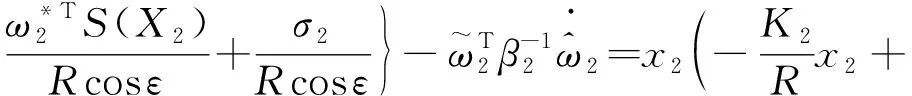
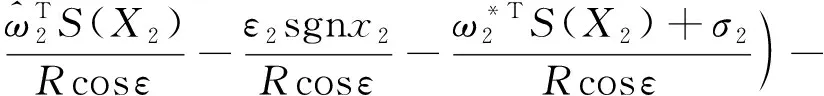
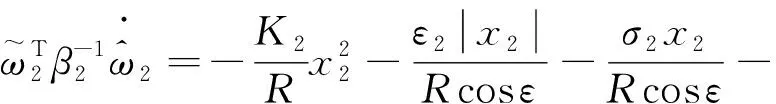
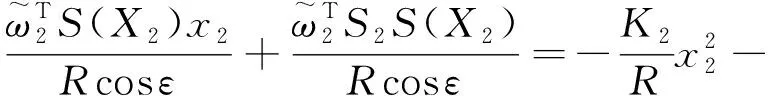
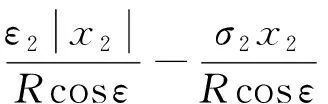
(25)
2.3 制导律的实现

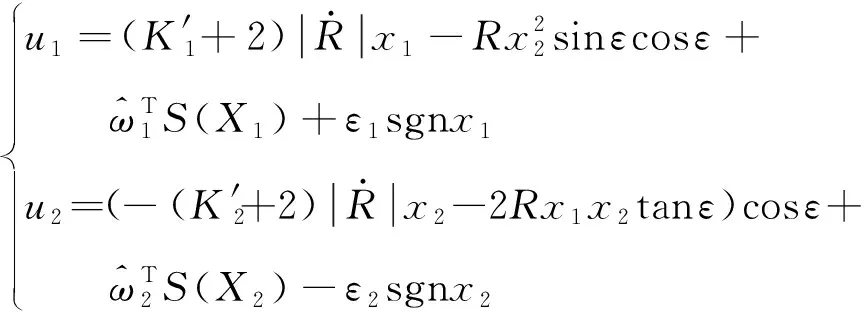
(26)
观察式(26)可知:整个制导律由四项组成,第一项与比例导引律类似;第二项是由于俯仰和偏航两个平面存在耦合;第三项和第四项是为了消除目标加速度与系统不确定性对系统的影响。
进一步为了减缓滑模抖振问题,采用连续高增益法,利用(||+)和(||+)代替sgn和sgn,则有

(27)
式中:和为较小的正数。
考虑到导弹制导指令的实现多是以法向过载的形式给出,式(27)所示的制导律和是在视线坐标系下设计,将其转换到弹道坐标系下。令为弹道坐标系下的控制输入,为弹道倾角,为弹道偏角,可得到
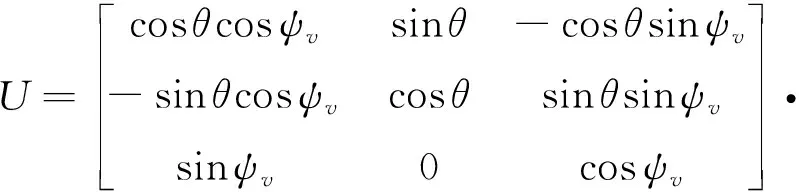
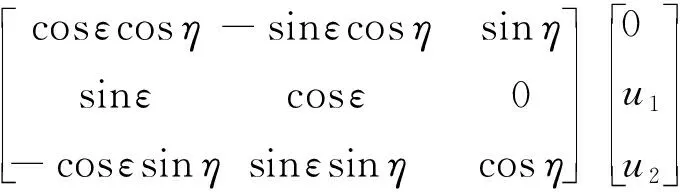
(28)
由于导弹纵向速度一般不做控制,因而在弹道坐标系下导弹制导系统的法向过载输入和为
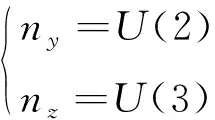
(29)
3 仿真校验
为验证所提基于RBF神经网络的滑模制导律的有效性,本节以三维空间目标拦截为场景,设计了三种不同的目标机动方式(匀速运动、常值机动和正弦机动),对所提方法进行仿真校验。同时,经典的比例制导和文献[14]所提的自适应滑模制导方法作为对比试验,验证了所提方法的优越性。
拦截导弹的基本参数为:质量1000 kg,横截面积0.45 m,特征长度0.7 m,=100 kg·m,==5700 kg·m,最大推力为5000 N,导弹和拦截目标的仿真初始参数如表1所示。所提制导方法的控制参数选取为:′=′=3,==2,=001,=005,==1,RBF网络的初始权重设置为0。比例制导过载指令为:
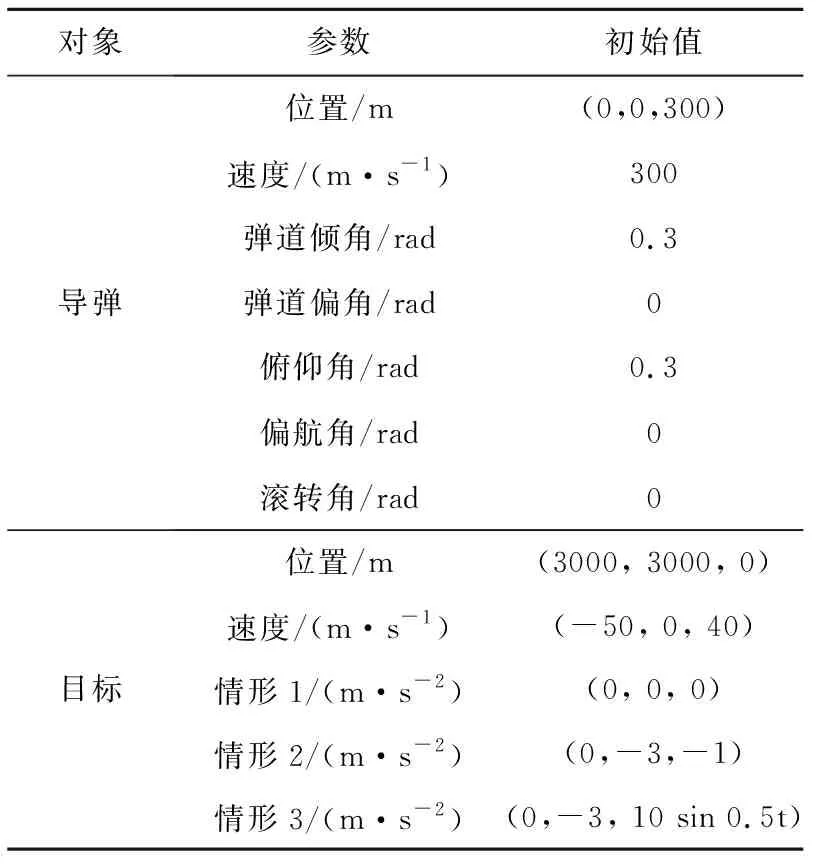
表1 弹-目仿真初始参数Table 1 Initial parameters of projectile-eye simulation

(30)
式中:导引系数==4,为导弹与目标的相对速度。为方便标记,仿真中用PN代表比例导引
律,ASMG代表文献[14]所提的自适应变结构制导律,RBFSMG代表本文所提的神经自适应滑模制导律。
仿真情形1:拦截目标做匀速运动
仿真结果如图3至图7所示。由图可知:当目标匀速运动时,三种制导方法都能够有效拦截目标,且制导性能都比较高,即导弹视线角速率都能趋于零,弹道比较平直。其中,图3为导弹及目标的空间轨迹。可以看出,导弹在三种制导律的作用下都成功拦截了目标,与PN相比,ASMG和RBFSMG作用下的导弹弹道更加平滑,更易于工程实现。
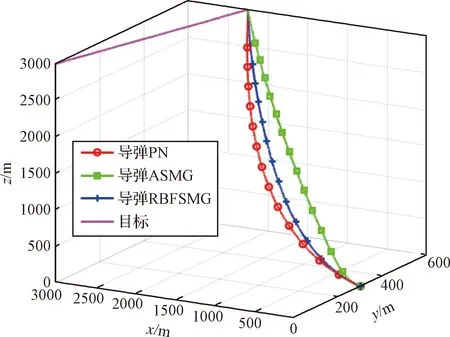
图3 三维拦截轨迹Fig.3 Three-dimensional interception trajectories
图4和图5分别表示俯仰平面和偏航平面的过载变化曲线。观察可知,当目标匀速运动时,三种制导方法作用下的过载指令都能够趋于零,但在整个拦截过程中,ASMG的过载收敛速度最快,大约在3 s收敛到零,且在零附近的范围内波动较小,RBFSMG的收敛速度次之,大约在9 s收敛到零,而PN的收敛速度最慢,收敛到零附近大约需要11 s。同时,ASMG和RBFSMG的初始过载幅度较大,俯仰平面是6.5,偏航平面是0.75,但会快速收敛到零附近,PN初始过载幅度比较小,在俯仰平面和偏航平面分别是5和0.3。
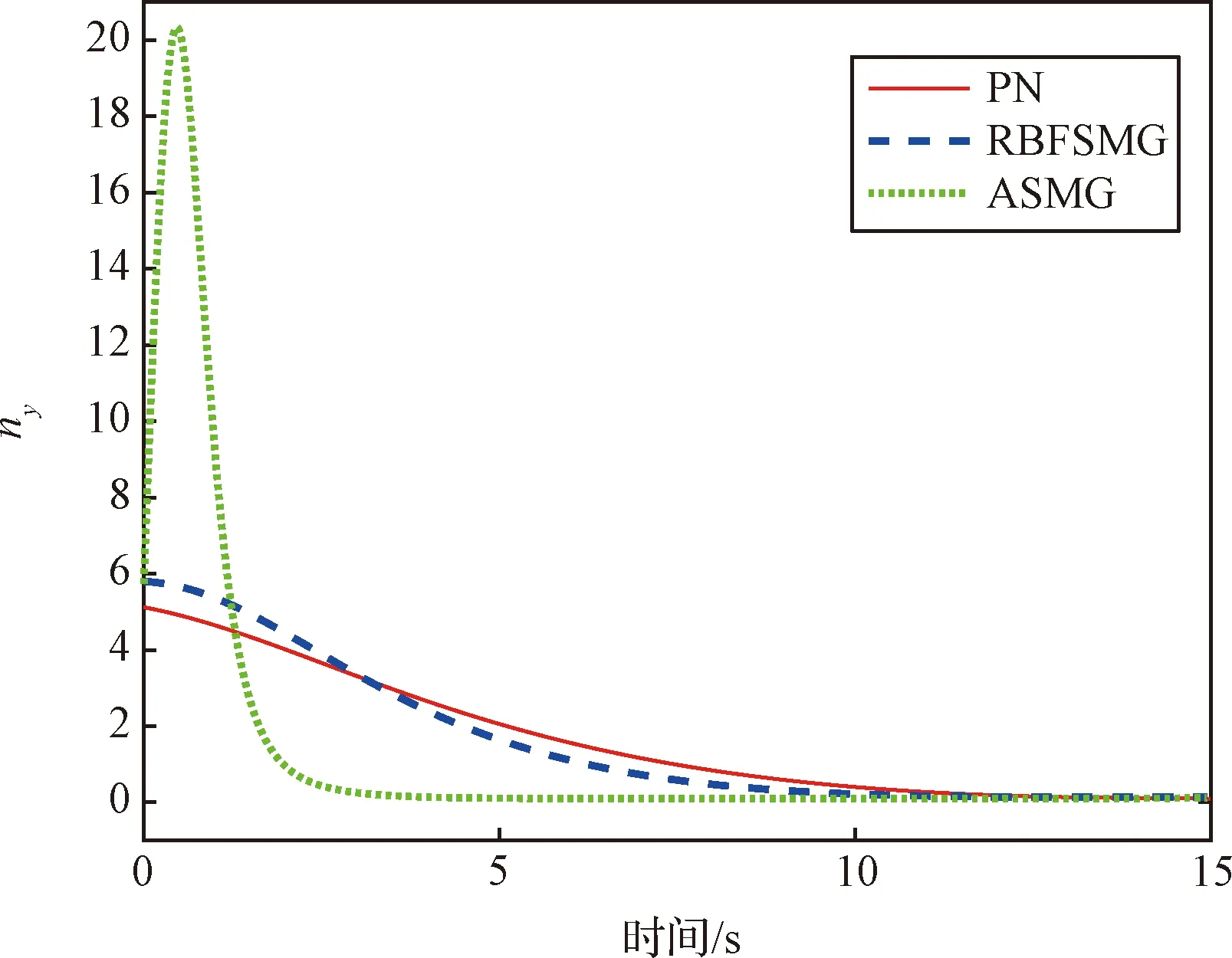
图4 ny响应曲线Fig.4 Respond curves of ny
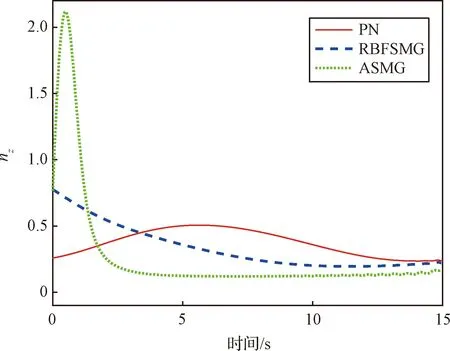
图5 nz响应曲线Fig.5 Respond curves of nz
图6和图7分别为导弹视线高低角速率和视线方位角速率响应曲线。观察可知,在三种制导方法作用下视线角速率收敛速度明显不同,俯仰平面内,视线角速率初值都为2.3 (°)/s的情况下,ASMG的收敛速度最快,大约在3 s收敛到零附近,而PN和RBFSMG的收敛速度较慢,大约在13 s收敛到零附近。视线角速率值在-0.1 (°)/s至0.1 (°)/s之间时,ASMG和RBFSMG的变化曲线基本重合,大约在2 s后收敛到零附近,而PN的收敛速度较慢,且在零附近波动。相比之下,RBFSMG控制下的视线角速率变化情况优于PN。
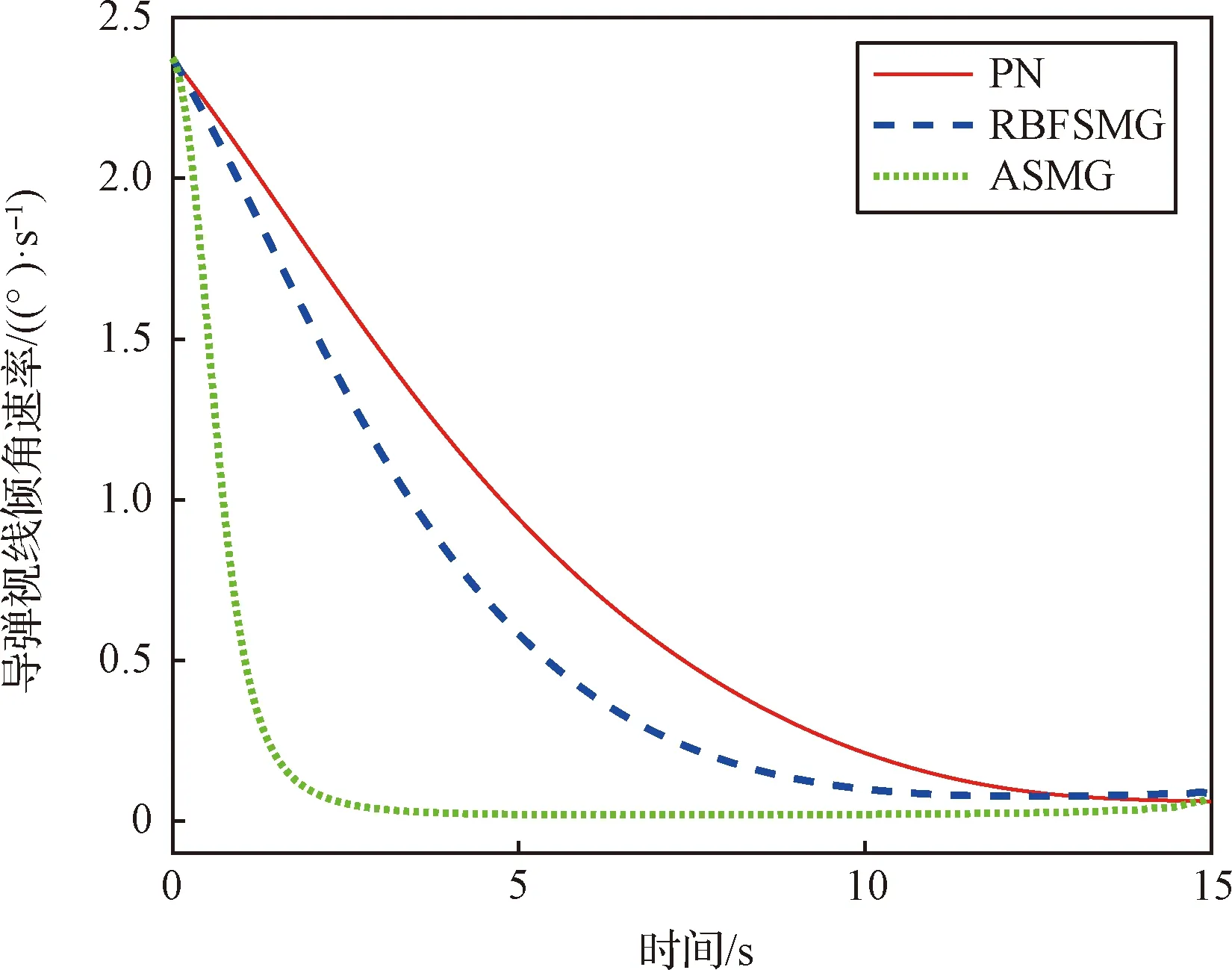
图6 响应曲线Fig.6
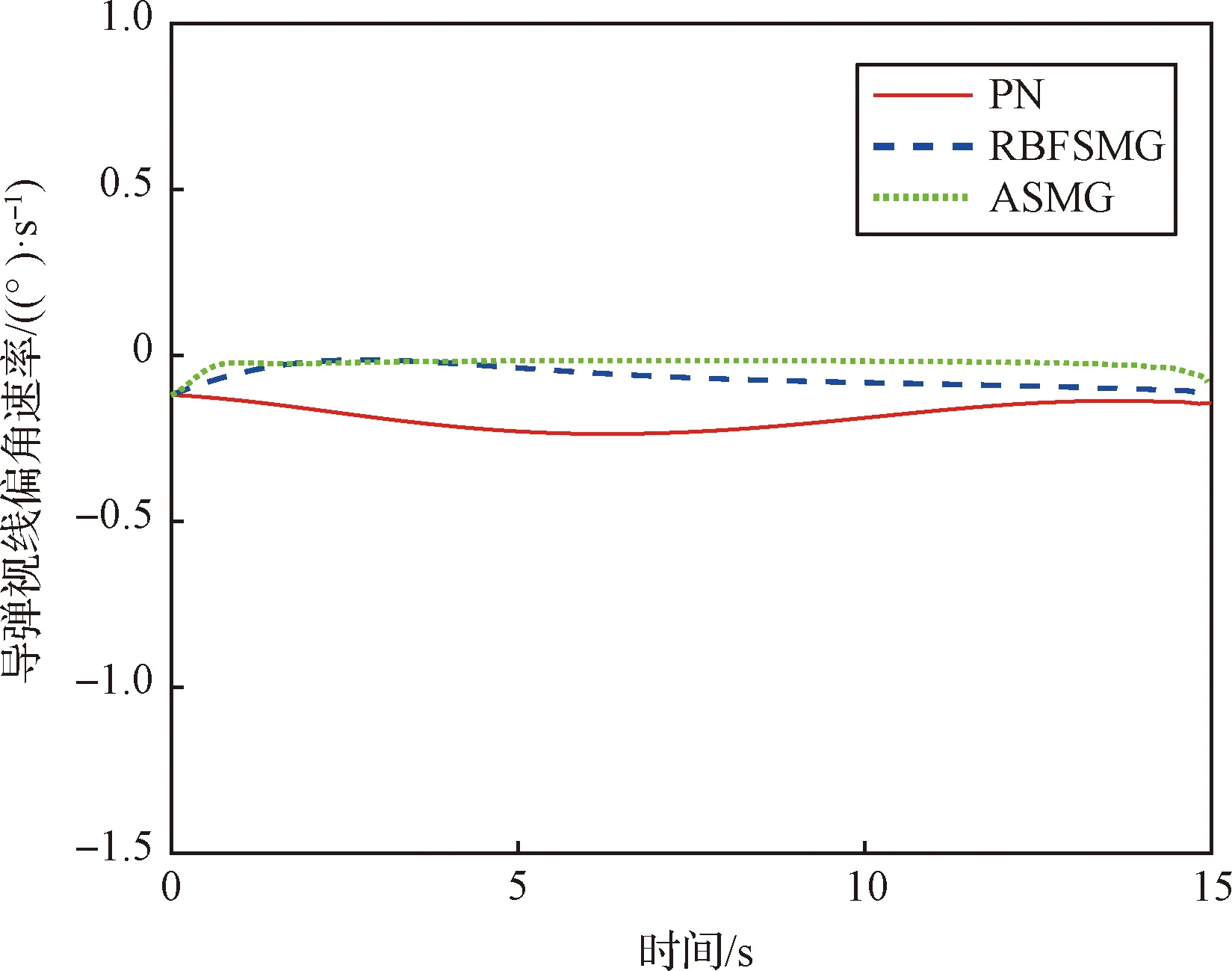
图7 响应曲线Fig.7
仿真情形2:目标常值机动
仿真结果如图8至图12所示。图8为导弹和目标的运动轨迹,由图可知:导弹在三种制导律的作用下成功拦截目标,与PN相比,ASMG和RBFSMG作用下的导弹弹道更加平滑,并且RBFSMG制导律弹道特性最优。图9和图10是导弹在俯仰平面和偏航平面的过载变化曲线。观察可知,三种方法作用下的导弹制导指令都能够趋于零,但在整个拦截过程中,ASMG和RBFSMG的过载收敛速度更快,大约在10 s收敛到零,且在零附近的波动范围较小,而PN的收敛速度较慢,大约在11 s收敛到零附近。同时从过载幅度来看,ASMG和RBFSMG的初始幅度较大,俯仰平面是6.7,偏航平面是0.75,但是RBFSMG会快速收敛到零,ASMG会出现波动,这是受逼近目标加速度所影响。PN初始过载幅度比较小,在俯仰平面和偏航平面分别是5和0.3。观察指令变化曲线可以看到,ASMG和RBFSMG在初始时刻充分利用过载,从而使得弹道比PN平滑。

图8 三维拦截轨迹Fig.8 Three-dimensional interception trajectories
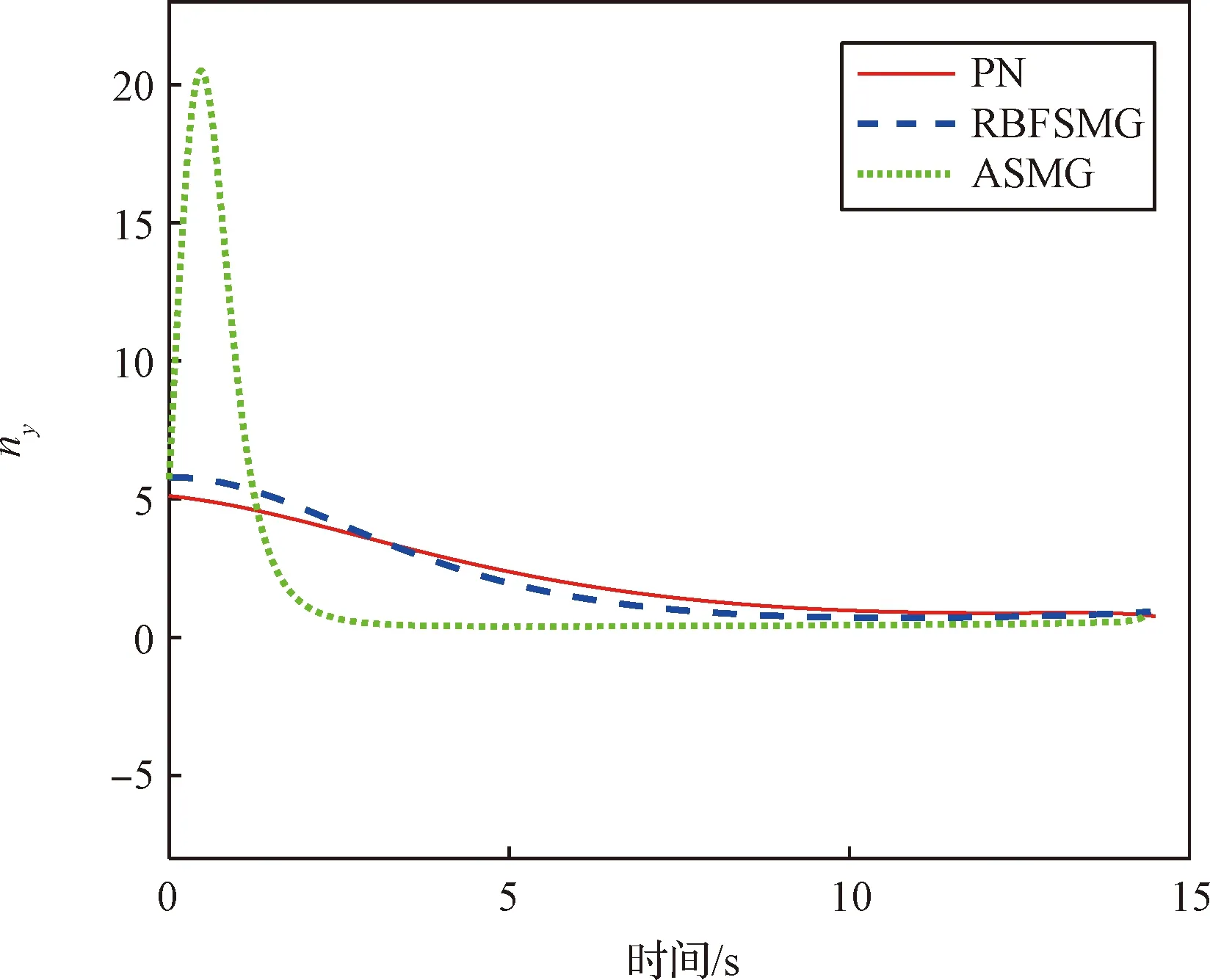
图9 ny响应曲线Fig.9 Respond curves of ny
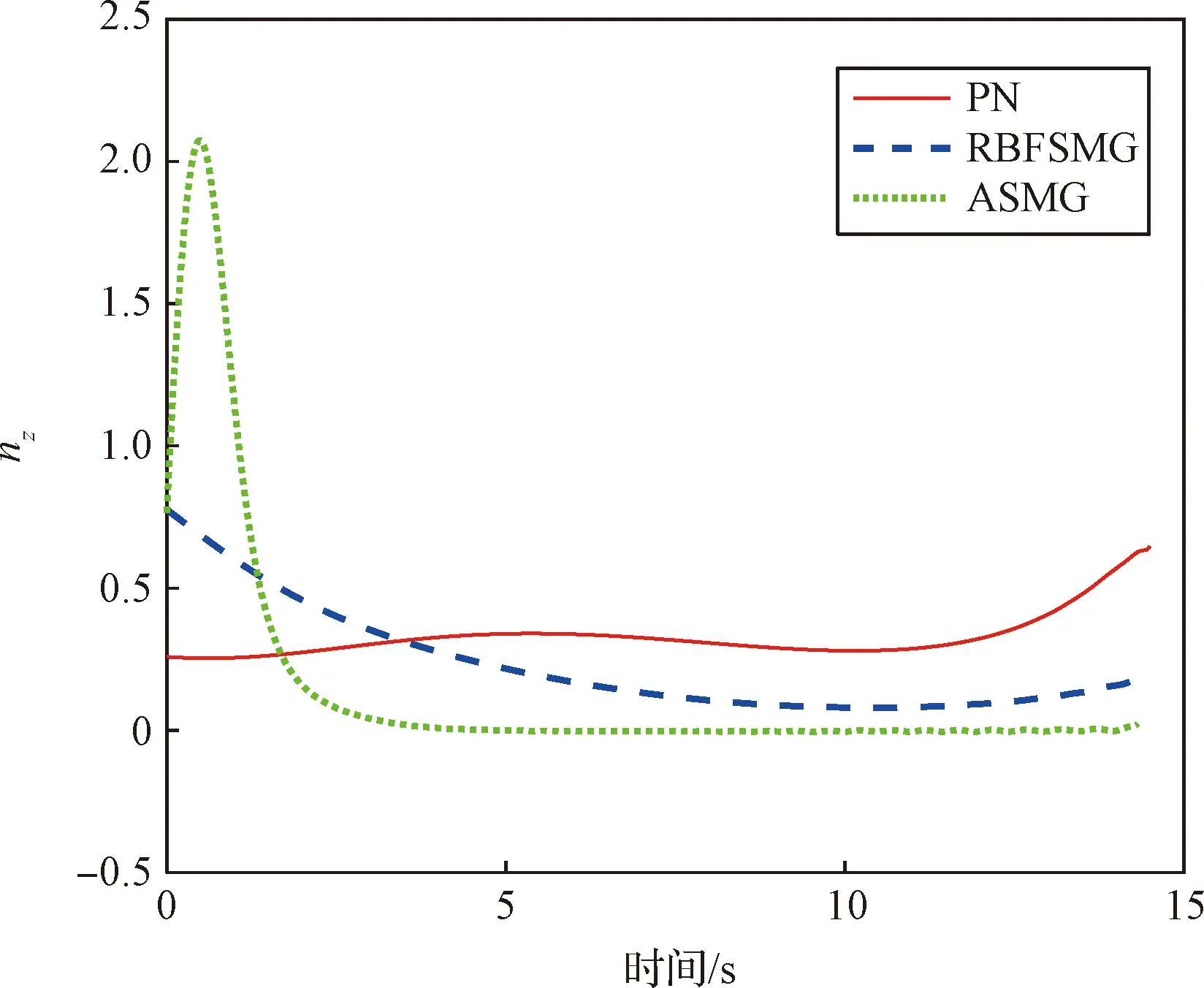
图10 nz响应曲线Fig.10 Respond curves of nz
图11和图12为导弹视线高低角速率和视线方位角速率响应曲线。观察视线角速率变化曲线可以得到,三种方法作用下视线角速率收敛到零的速度和程度明显不同。俯仰平面下,ASMG和RBFSMG视线角速率收敛速度最快,大约在10 s调整到零附近,而PN视线角速率收敛速度较慢,且在目标拦截成功时都未调整到零附近。偏航平面下,ASMG和RBFSMG的视线角速率变化曲线基本重合,大约在3 s调整到零附近,而PN视线角速率收敛速度较慢,且在临近拦截时刻还出现了发散现象。图13为拦截目标加速度信息的估计误差响应曲线,由图可知,估计误差大约在5 s内收敛到零。
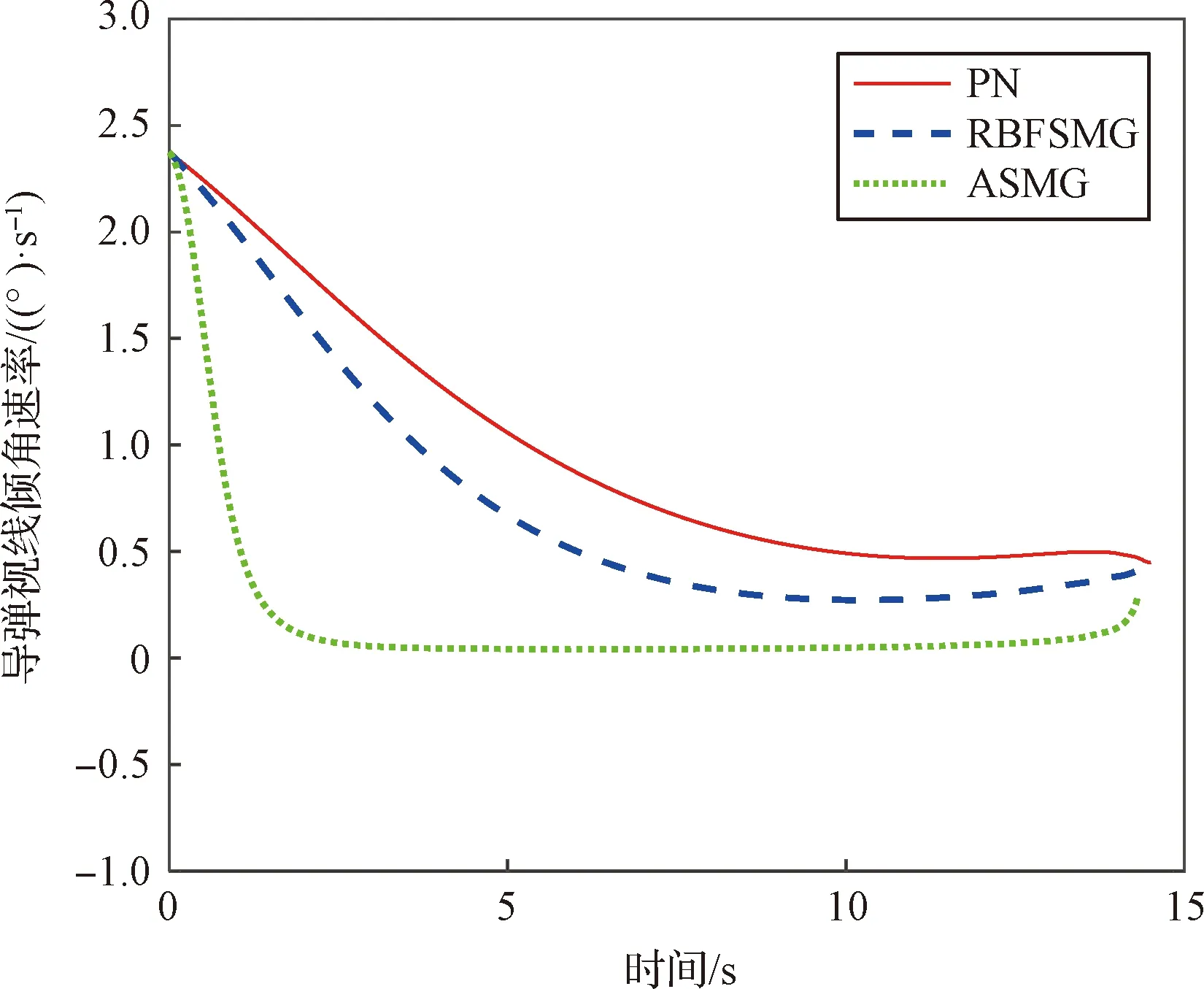
图11 响应曲线Fig.11

图12 响应曲线Fig.12
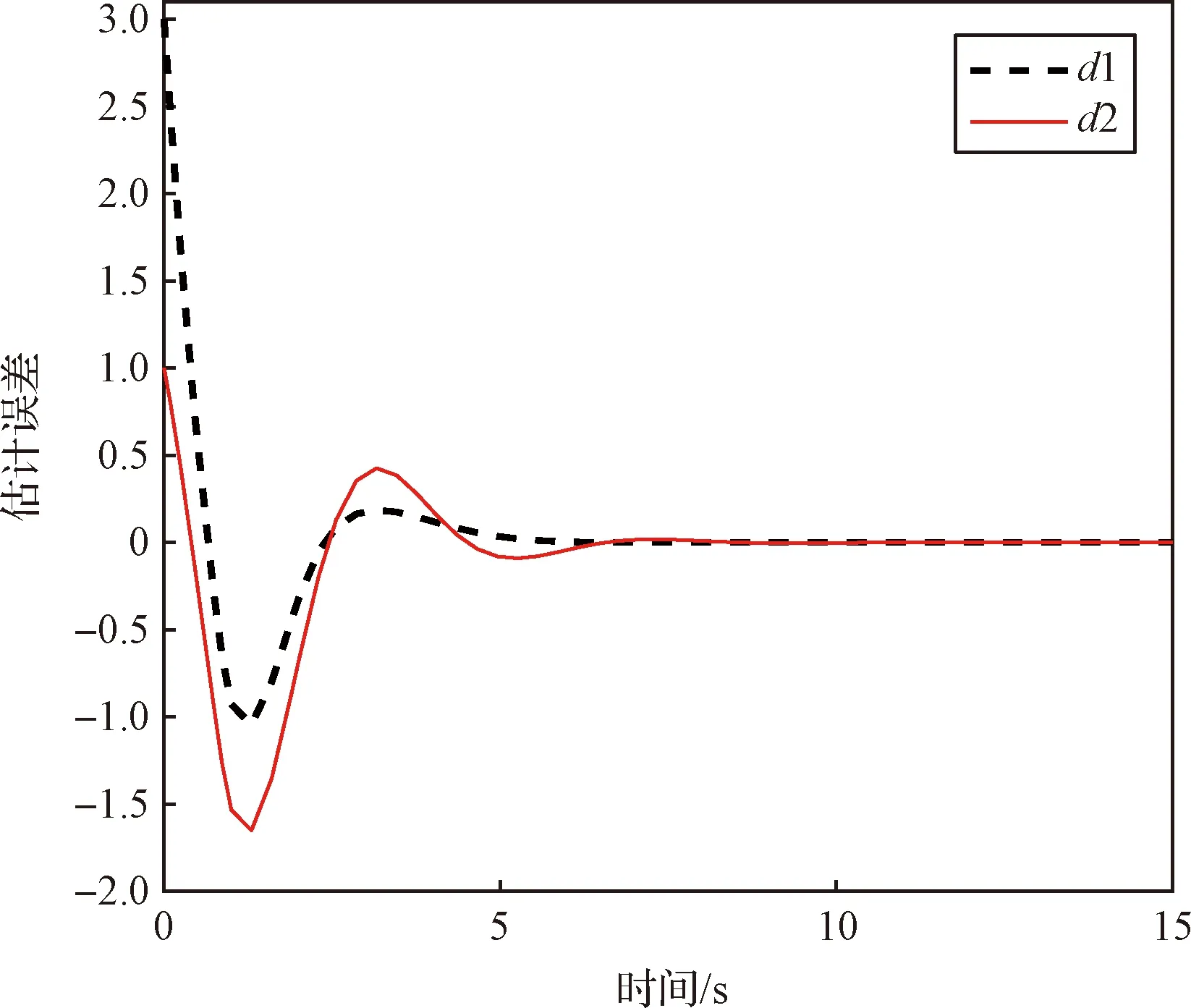
图13 估计误差响应曲线Fig.13 Respond curves of estimation errors
仿真情形3:目标正弦机动
仿真结果如图14至图18所示。观察可知:当目标做正弦机动时,三种制导方法都能够有效拦截目标,但在制导性能方面,本文所设计的神经自适应滑模制导方法明显优于另外两种方法,在视线角速率变化趋势上,PN会出现发散现象,而ASMG和RBFSMG视线角速率波动范围较小。从图14中可以看出,导弹在三种制导律的作用下成功拦截目标,与PN相比,RBFSMG作用下的弹道更加平滑,对目标加速度响应更为灵敏。
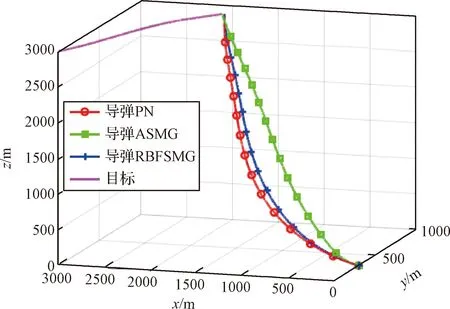
图14 三维拦截轨迹Fig.14 Three-dimensional interception trajectories
图15和图16是导弹在俯仰平面和偏航平面的过载变化曲线。由图可知,三种制导方法作用下的制导指令都在零附近小范围波动,但在整个拦截过程中,ASMG和RBFSMG制导指令的范围内波动较小。从过载幅度来看,ASMG和RBFSMG的初始过载幅度比较大,受智能逼近目标加速度的影响,ASMG会出现较大波动,俯仰平面过载幅值为22。PN初始过载幅度比较小,在偏航平面波动较为剧烈。
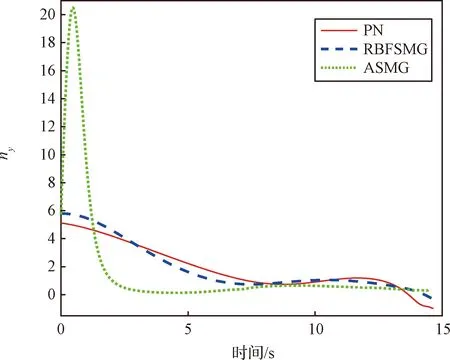
图15 ny响应曲线Fig.15 Respond curves ofny
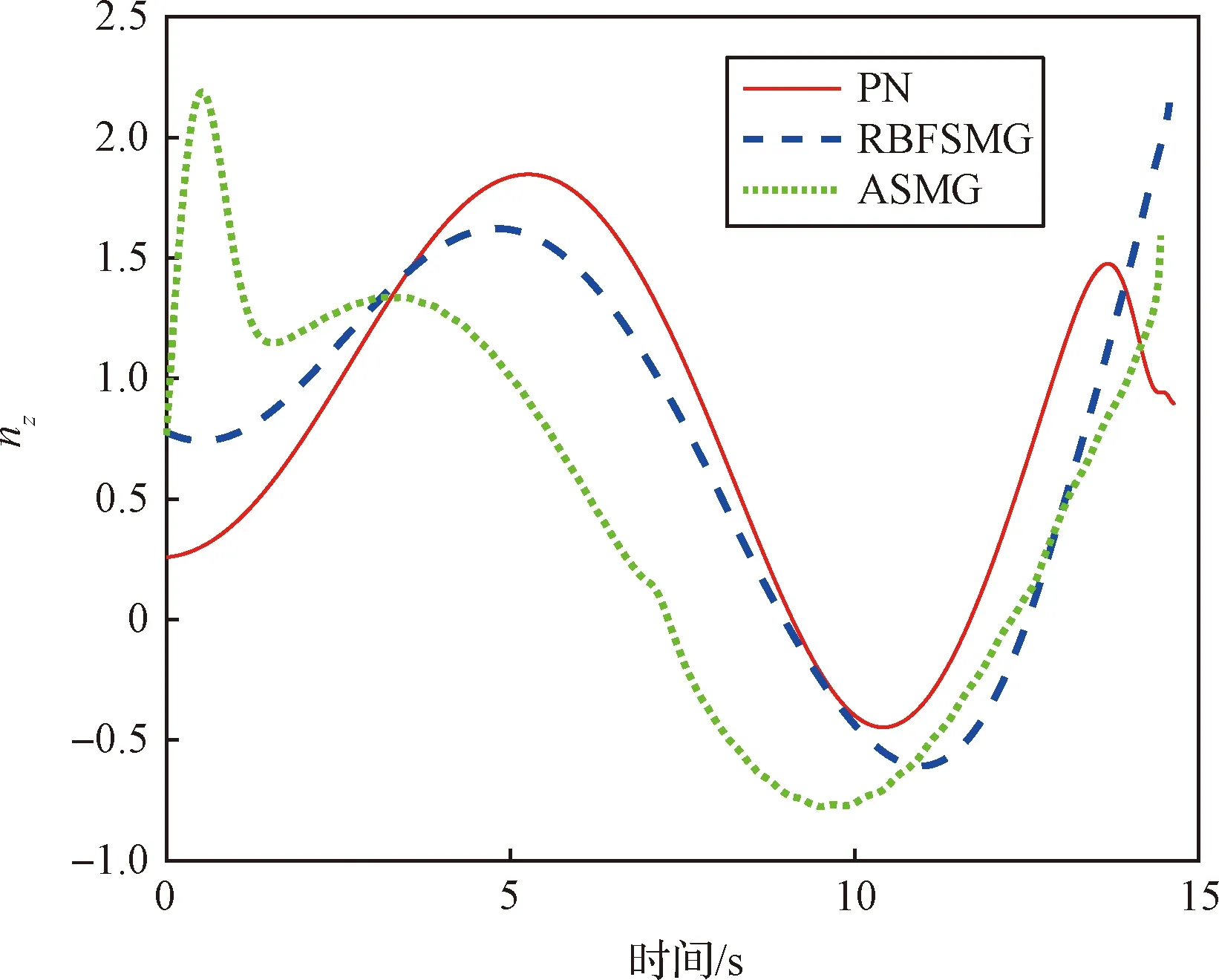
图16 nz响应曲线Fig.16 Respond curves ofnz
图17为拦截目标加速度信息的估计误差响应曲线,图18和图19为导弹视线高低角速率和视线方位角速率响应曲线。由视线角速率变化曲线可知:三种制导方法作用下视线角速率都将收敛到零,且存在小范围的波动。俯仰平面中,ASMG和RBFSMG视线角速率收敛速度最快,大约在12 s收敛到零附近,而PN的视线角速率收敛速度较慢,且在目标拦截成功时都未调整到零附近。偏航平面下,ASMG和PN的视线角速率波动幅度较小,而RBFSMG视线角速率波动幅度较大,最大为14 (°)/s。
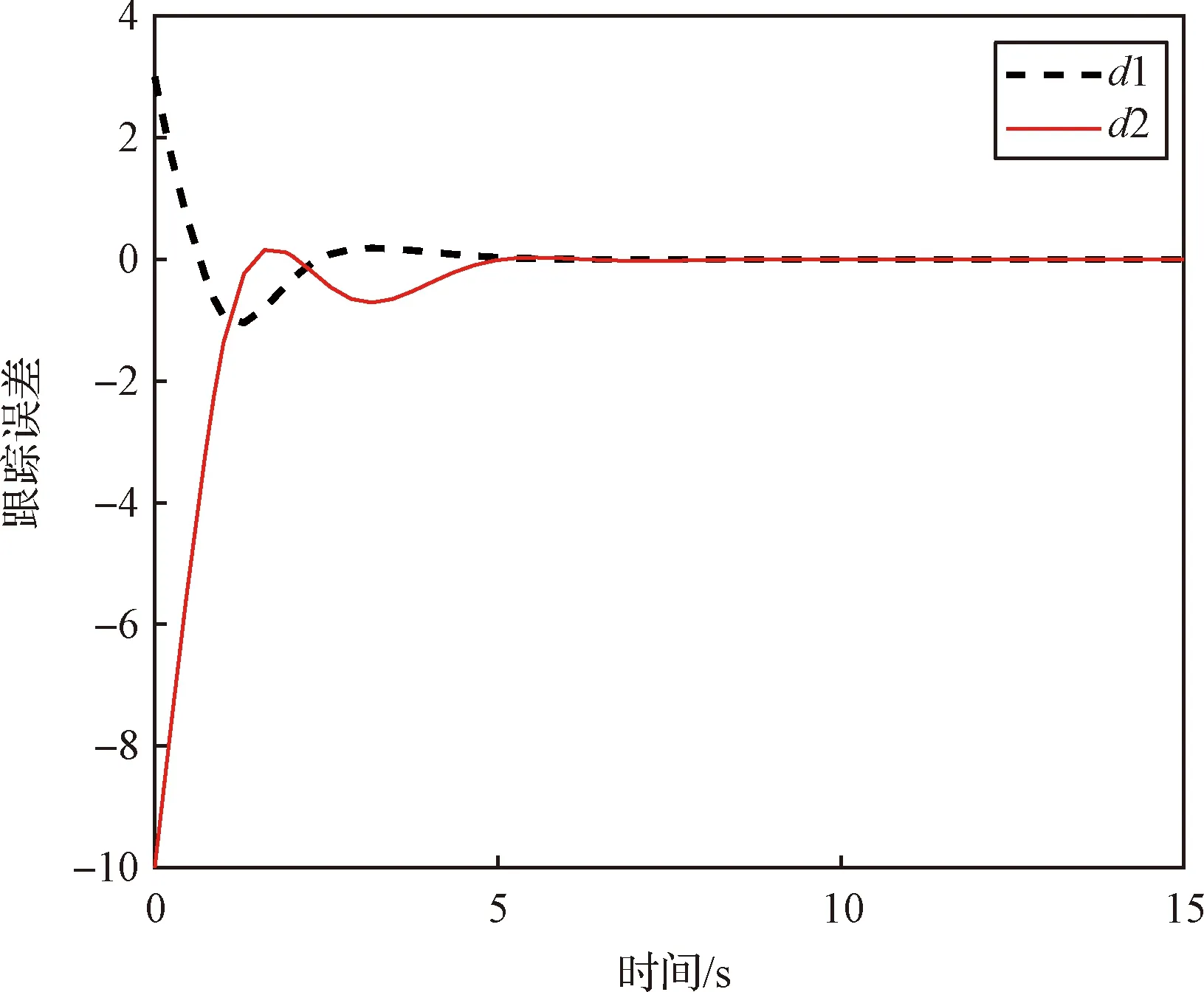
图17 估计误差响应曲线Fig.17 Respond curves of estimation errors

图18 响应曲线Fig.18
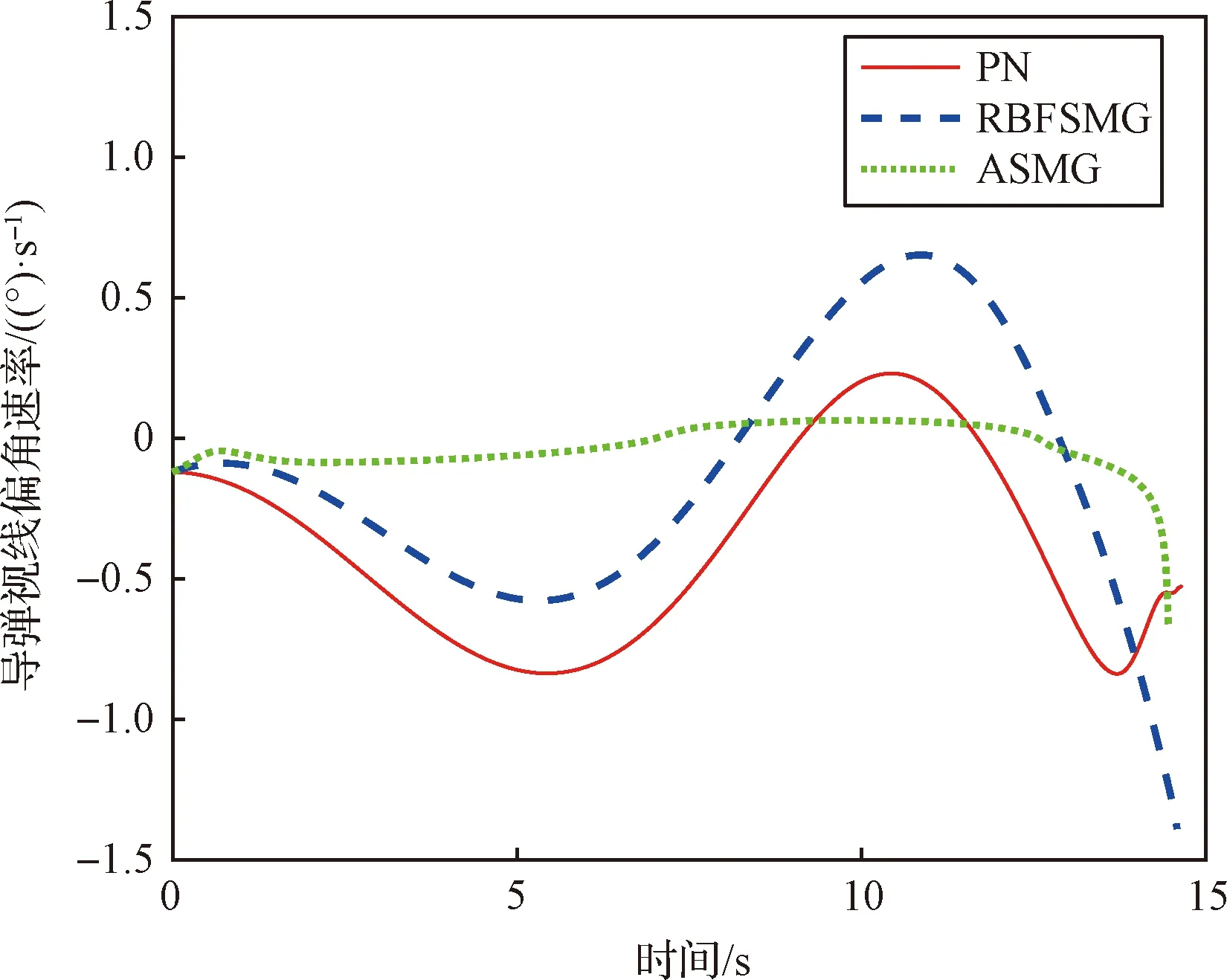
图19 响应曲线Fig.19
结合上述仿真结果可知,当目标匀速运动时,三种制导方法都有不错的拦截效果,甚至PN方法还要优于ASMG和RBFSMG,这是由于本文所设计的制导律对目标加速度进行了估计,具有较强的灵敏性,目标加速度为零,会产生估计误差,使得制导指令出现偏差。当目标机动时,本文所设计的神经自适应制导方法的制导效果明显优于PN制导律,主要表现为更优的弹道特性和较快的视线角速率收敛速度。这是因为RBFSMG制导方法不仅估计了目标加速度,而且补偿了俯仰平面和偏航平面的耦合,从而对目标加速度响应灵敏。此外,与PN相比较,本文所提的制导方法所需过载较大,这是因为制导律可以消除俯仰和偏航两个平面耦合关系对系统的影响,以及消除目标加速度对系统的影响,从而会产生较大的过载指令。RBFSMG制导方法的有效性主要表现在弹道特性和角速率收敛速度上面,并且还具有一定的鲁棒性,当目标机动时,所提制导方法能够较好地估计出加速度,使得导弹制导不受影响,精确拦截到目标。
4 结 论
本文针对拦截目标加速度信息难以捕获的实际情况,提出了一种基于RBF神经网络的自适应滑模制导律,完成了三维空间机动目标的拦截制导任务。所提方法利用神经网络的高效逼近能力,有效估计了目标机动的加速度信息,在此基础上结合滑模变结构控制方法的良好鲁棒性,分别对导弹俯仰平面和偏航平面设计了对应的自适应滑模制导律。同时连续高增益法被用来处理符号函数,以削弱系统抖振,并根据导弹制导实现的具体情况,给出了弹道坐标系下的法向过载,仿真结果表明本文所提的基于RBF神经网络的自适应滑模制导控制律具有良好的制导拦截效果。

