一种地理系下基于伪线性模型的捷联惯导算法

杨小康，严恭敏，李思锦，李四海，刘明雍

(1. 西北工业大学自动化学院，西安 710129; 2. 陕西省飞行控制与仿真技术重点实验室，西安 710129;3. 西安微电子技术研究所，西安 710065; 4. 西北工业大学航海学院，西安 710072)

0 引 言

捷联式惯导系统与平台式不同，需要利用陀螺仪数据完成姿态解算，构建虚拟的数学平台，再利用加速度计数据实现速度和位置解算。因此捷联惯导系统的导航解算算法相较于平台系统更加复杂，也更加重要，捷联惯导算法研究也一直是捷联惯导系统的研究重点。目前受制于惯导器件精度，惯导算法研究的主要方向是组合导航、冗余惯导系统、长航时误差抑制等。但是原子陀螺惯导系统、空天飞机、高超音速飞行器等新的应用场景对捷联惯导解算算法提出了新的挑战，需要针对捷联惯导解算的算法结构或原理进行改进。在传统捷联惯导算法发展过程中，随着对算法误差机理研究的深入，算法精度不断提高。文献[6]利用等效旋转矢量完成姿态解算，建立了捷联惯导算法的基础。在此基础上，文献[7-8]又进一步提出了多子样捷联惯导算法，通过补偿圆锥误差和划桨误差提升算法精度。

由于构成捷联惯导系统的陀螺仪和加速度计精度提升，加之大机动高动态条件下导航需求的出现，近几年的捷联惯导算法研究重点是提升捷联惯导算法精度。文献[9]通过建立姿态更新不可交换误差的高阶误差模型提出了基于角增量四次叉乘补偿项的高精度捷联惯导算法。文献[10]提出使用数值仿真算法求解不可交换误差高阶补偿系数，实现此类算法中补偿系数的快速计算。文献[11-12]则是基于函数迭代方法，构建角速度和比力多项式并完成高精度导航解算。

无论是传统的多子样捷联惯导算法还是新提出的几种高精度捷联惯导算法，都是利用姿态阵、四元数、罗德里格参数等进行姿态解算，再根据对应的坐标转换计算规则，将载体坐标系下的加速度计输出转换到导航坐标系下。因为以上表示姿态的变量并不是在线性空间中定义的，所以速度更新方程是非线性的，不便于直接利用捷联惯导系统模型进行系统分析、滤波等操作。文献[13]介绍了伪线性系统相关算法基础，伪线性系统是指形似线性系统实则非线性系统的系统。文献[14-15]介绍了伪线性系统方法在卫星姿态控制、飞行器制导与控制中的应用。如果构建出捷联惯导系统的伪线性系统模型，就可以直接使用线性系统理论完成捷联惯导更新，直接使用捷联惯导系统模型构建线性Kalman滤波器实现初始对准、组合导航等，无需考虑模型的非线性问题。按照此研究路线，文献[16]提出了基于时间序列的惯性系下伪线性捷联惯导算法，建立了完整的伪线性捷联惯导算法，但是此算法建立在惯性系下，不能满足通常的导航系下定位需求，因此也不能直接将此模型应用于初始对准和组合导航中。

本文在伪线性模型相关理论和文献[16]中伪线性捷联惯导算法基础上，提出地理系下伪线性高精度捷联惯导更新算法。与传统的捷联惯导算法相比，伪线性的算法不再将一个完整的惯导更新过程分为姿态更新、速度更新和位置更新三部分，而是使用新构建的导航向量统一表示姿态、速度和位置信息，并且根据导航向量微分方程设计离散的导航向量更新算法。应用伪线性捷联惯导算法的惯导系统结构如图1所示，原有的三个更新回路被导航向量及其线性更新方程代替，更新后的导航向量再转换成姿态、速度和位置输出导航结果。伪线性捷联惯导算法因采用了基于泰勒级数展开的数值算法，因此在大机动或圆锥运动等能激励出较大不可交换误差的情况下，理论算法精度远高于传统算法。除此之外，捷联惯导系统伪线性模型的另一优势是可以使用线性的分析与计算方法。

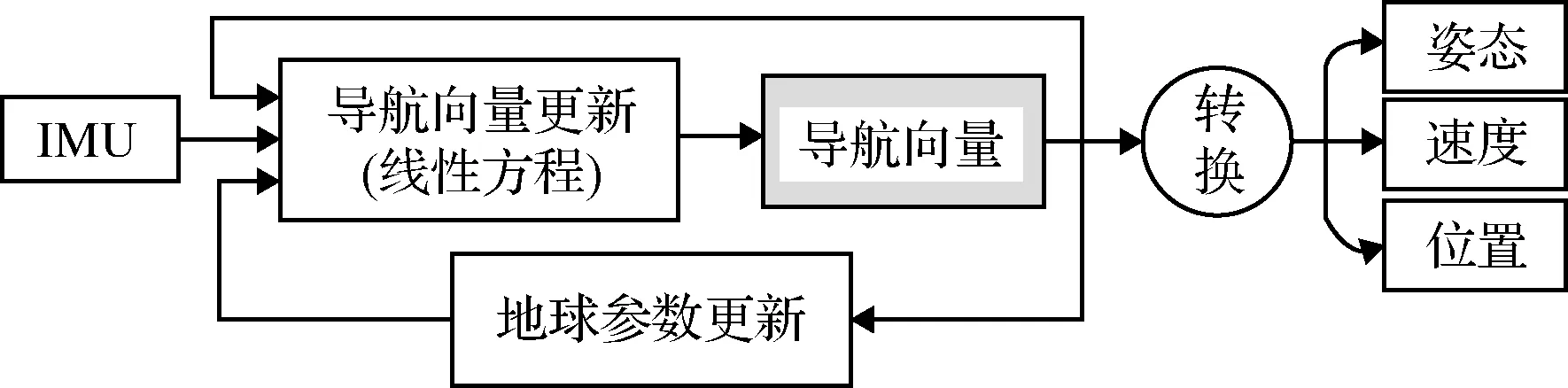
图1 伪线性捷联惯导系统结构Fig.1 Structure of pseudo-linear SINS

最后，为了验证基于伪线性模型的捷联惯导算法与传统算法的差异，用两种算法分别完成了大机动条件下导航解算和旋转弹飞行仿真导航解算，并比较两者的导航误差。

1 伪线性SINS更新公式

和传统的捷联惯导算法类似，伪线性算法模型也将按照姿态、速度和位置三个更新过程进行分析。在捷联惯导更新算法的推导过程中，表示惯性坐标系，表示载体坐标系，表示导航坐标系，表示地球坐标系。

1.1 姿态更新

在捷联惯导算法中姿态四元数微分方程为

(1)

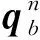
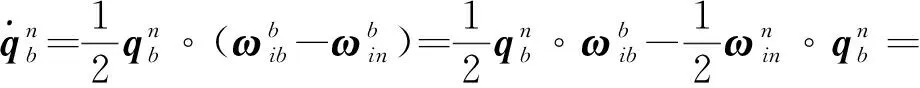
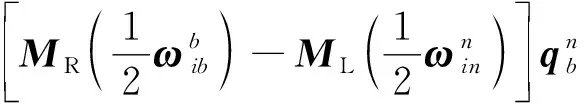
(2)

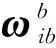
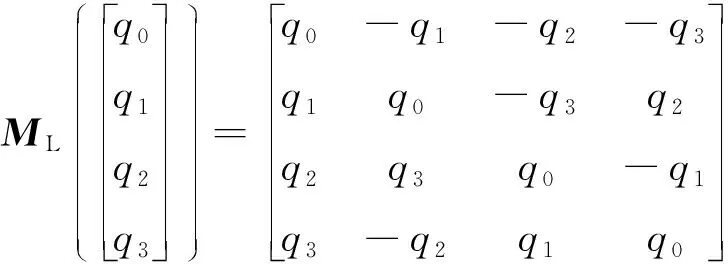
(3)

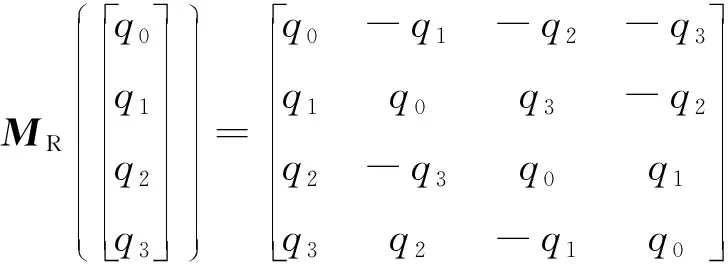
(4)

用表示式(1)模型中的系统矩阵，即

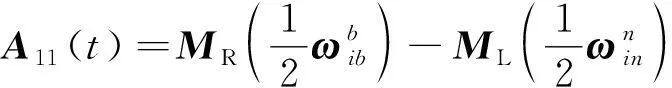
(5)

则导航解算的姿态更新可以表示为

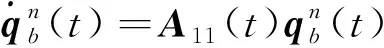
(6)

1.2 速度更新

比力方程是捷联惯导解算的核心之一，求解比力方程即可完成速度更新。捷联惯导系统导航系下比力方程为

(7)

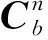
在式(7)中改用四元数将系下的比力转换到系下，得到：

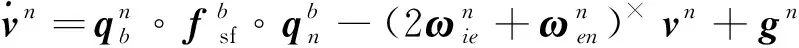
(8)

由式(8)右边第一项可以看出来，使用四元数进行导航解算时，速度更新方程是非线性的。

为了得到线性的速度更新方程，对速度向量进行变换，定义新的速度向量——速度四元数

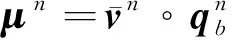
(9)

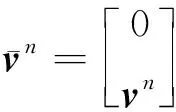
对式(9)两边求导

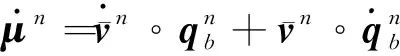
(10)

将式(8)写成四元数形式

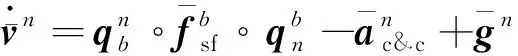
(11)

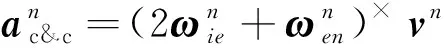
将式(2)和式(11)代入式(10)，得

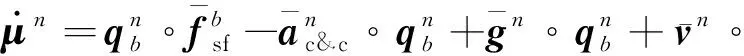
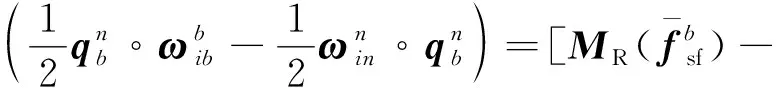
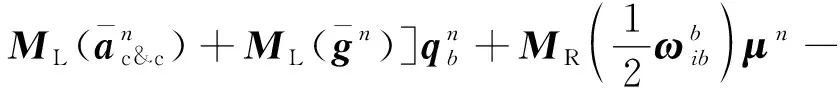
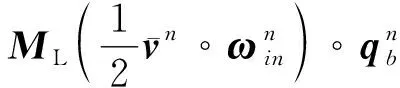
(12)

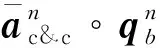
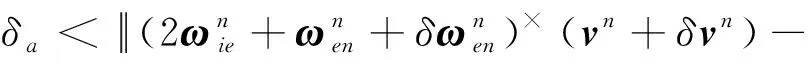
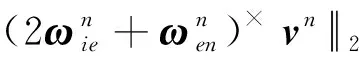
(13)

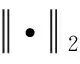
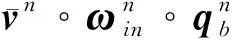
式(12)可整理成

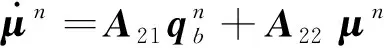
(14)

式中：

(15)

显然，式(14)中的速度微分方程是关于姿态四元数和速度四元数的线性方程。

1.3 位置更新

在地理系下通常计算载体所在纬度、经度和高度作为位置更新结果，因此定义位置向量

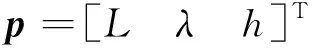
(16)

式中：为纬度，为经度，表示高度。其微分方程为

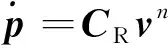
(17)

式中：

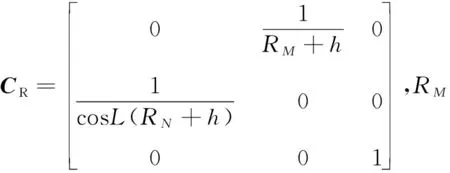
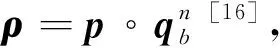
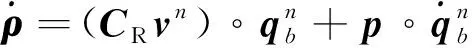
(18)

根据式(18)不能直接得出位置四元数与速度四元数之间的线性关系，所以需要研究新的位置四元数定义。

由式(9)得

(19)

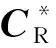
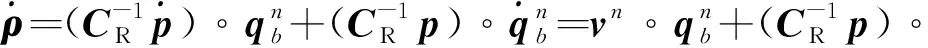
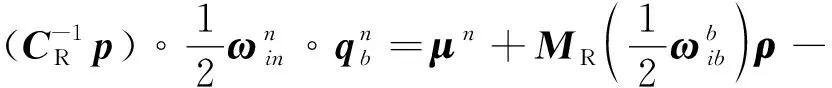
(20)

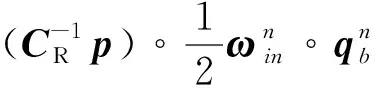
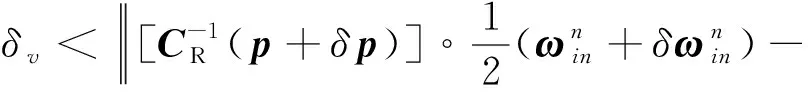
(21)

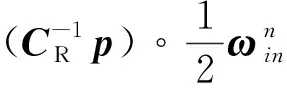
式(20)写成矩阵形式为

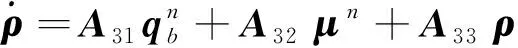
(22)

式中：

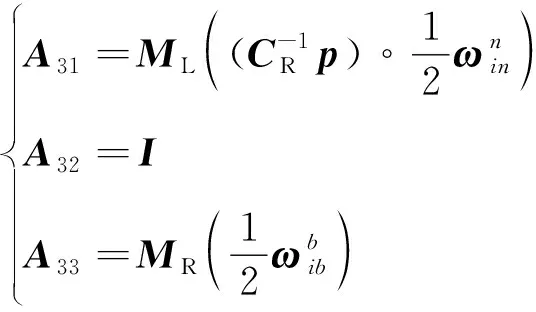
(23)

通过构建位置四元数向量，位置更新方程被转换成关于姿态四元数、速度四元数和位置四元数的伪线性方程。

2 导航向量及其更新方案

四元数微分方程为线性方程，比力方程虽然是非线性方程，但是经过变换得到的速度四元数微分方程是线性的，同理通过定义位置四元数得到了伪线性的位置更新方程，因此可以定义包含四元数、速度四元数和位置四元数的导航向量

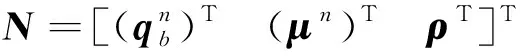
(24)

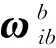
(25)

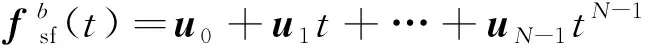
(26)

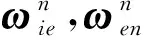
然后由式(6)、式(14)和式(22)可得导航向量微分方程

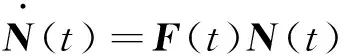
(27)

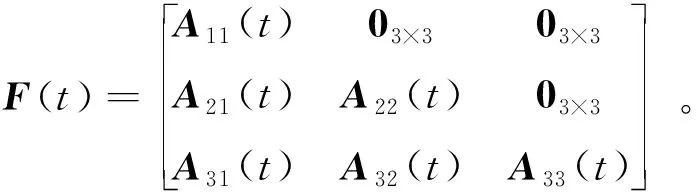
()=++…+-1-1

(28)

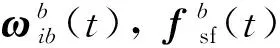
式(27)是线性时变系统，因此在任意更新周期内，状态转移矩阵满足：

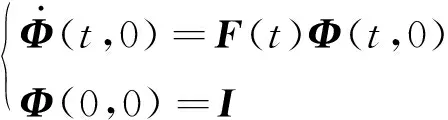
(29)

为了求解式(29)，将(,0)表示成关于时间的次矩阵多项式，即

(,0)=+++…+

(30)

对式(30)求导可得

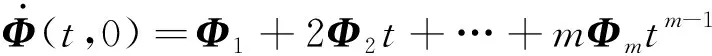
(31)

将式(28)、(30)和(31)代入式(29)，得

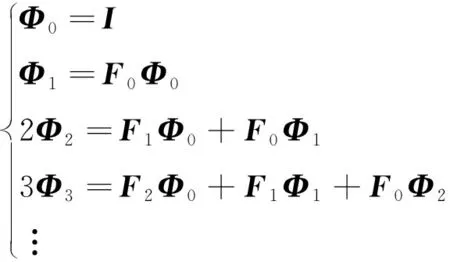
(32)

整理后得：

(33)

式中：是(,0)的展开次数，决定其计算精度，根据式(30)构建状态转移矩阵的精度可以达到(+1)，因此在设计算法时可以根据更新周期、导航算法精度等指标选择合适的展开次数完成计算。

根据式(28)、(30)和(33)可以计算出状态转移矩阵(, 0)，然后完成导航向量的更新

()=(, 0)(0)

(34)

最后将更新后的导航向量转换成地理系下的姿态、速度和位置。

3 算法精度评估

为了检验伪线性模型的导航解算效果，在短时大角速度大加速度条件和设计的旋转弹飞行轨迹上进行纯惯性导航解算，比较伪线性惯导算法与传统惯导算法的差异，计算时统一采用4子样算法结构。为便于表述评估结果，后文中使用“NLNA(Nonlinear navigation algorithm,非线性导航算法)”表示传统的捷联惯导算法，用“PLNA(Pseudo-linear navigation algorithm,伪线性导航算法)”表示新提出的捷联惯导算法。

伪线性算法的4子样解算结构如下：

① 根据4子样角增量和速度增量Δ,…,Δ和Δ,…,Δ，计算角速度和比力多项式系数，得到角速度和比力函数：

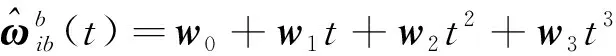
(35)

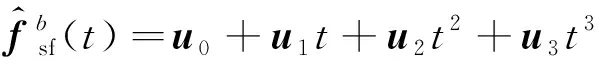
(36)

② 根据式(6)、式(14)和式(22)得到不同次系统矩阵的各个子矩阵。0次系数矩阵中各项如下：

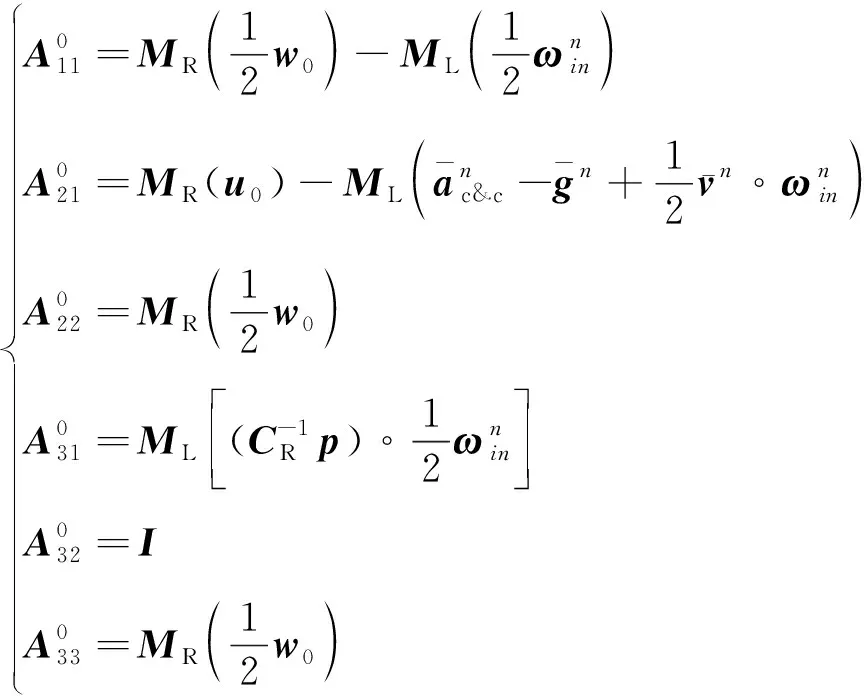
(37)

1次及以上系数矩阵各项为：

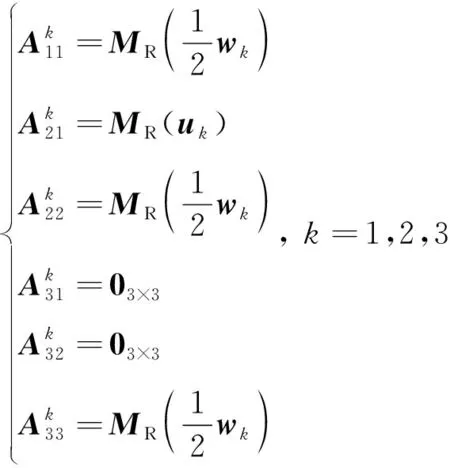
(38)

③ 根据式(27)得到不同次系数矩阵

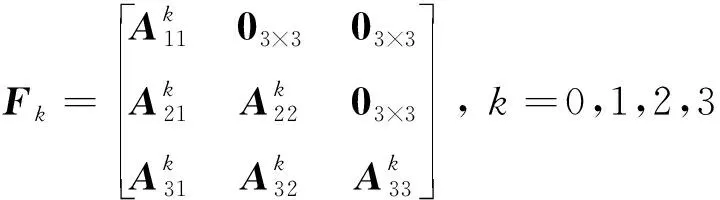
(39)

并根据式(28)得到导航向量系统矩阵的多项式形式：

=+++

(40)

④ 将代入式(33)得到状态转移矩阵不同次项，按照式(30)计算状态转移矩阵

(,0)=+++

(41)

⑤ 最后根据式(34)完成导航向量更新，并根据式(9)和式(11)中的定义计算出地理系下的速度和位置信息。

3.1 大机动条件惯导解算仿真

大机动运动条件对捷联惯导算法有更高的要求，对于传统捷联惯导算法，在大机动条件下会激励出较大的算法误差。捷联惯导算法研究中一般都采用多项式形式的角速度和加速度模拟大机动条件，并在此条件下检验算法精度。按照文献[18-19]中仿真方法，用角速度多项式模拟大机动角运动，设置大机动条件角速度和加速度多项式如式(42)～(43)所示，对应的角速度与加速度变化如图2所示。仿真时按1 kHz采样得到惯导仿真数据，同时以100 kHz采样完成2子样导航解算，得到姿态和速度的参考结果。两种捷联惯导算法的姿态误差和速度误差如图3～4所示，导航解算误差如表1所列，因为不同算法的姿态和速度误差相差较大，因此不必全部列出，选取导航结束时刻的三个轴上误差的模值作为姿态误差和速度误差。

图2 大机动条件角速度与加速度Fig.2 Angular rate and acceleration in high-dynamic condition

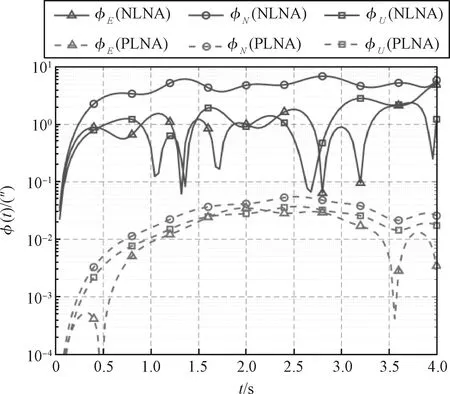
图3 大机动条件姿态误差Fig.3 Attitude errors in high-dynamic condition

图4 大机动条件速度误差Fig.4 Velocity errors in high-dynamic condition

(42)

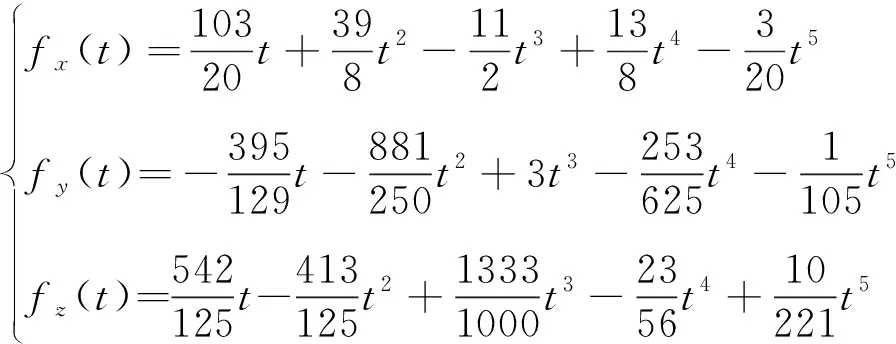
(43)

从图3～4和表1中的姿态误差与速度误差对比结果可以明显看出伪线性算法的导航误差更小。

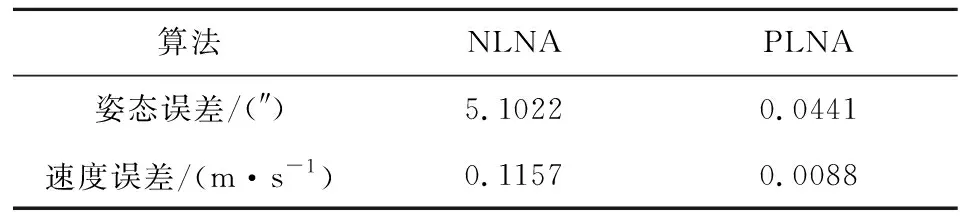
表1 导航解算仿真误差Table 1 Errors of navigation solution simulation

这是因为基于伪线性模型的算法在进行姿态和速度更新时，通过求解姿态和速度微分方程的高阶导数，计算出高精度的导航结果。在角速度和加速度为关于时间的一般多项式的条件下，此算法可以通过增加泰勒展开次数减小算法误差，这一特点也使得伪线性捷联惯导算法更加适合应用于大机动条件。

3.2 旋转弹纯惯性导航仿真

旋转弹飞行过程中含有较长的大角速度机动，容易激励出捷联惯导算法误差，因此和传统算法相比，伪线性模型捷联惯导算法更加适用于旋转弹捷联惯导解算。为了验证捷联惯导算法性能，设计旋转弹飞行过程仿真轨迹如图5所示，飞行中弹体角速度从20π rad/s逐渐减速至2π rad/s，惯导数据更新频率为1 kHz。

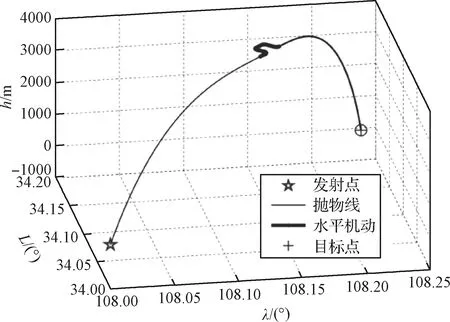
图5 旋转弹仿真轨迹Fig.5 Simulation trajectory of spinning projectile

使用4子样算法捷联惯导解算仿真并统计姿态误差、速度误差和位置误差的均方根以分析导航误差，评估两种算法的精度。导航误差对比如图6～7所示，全程的均方根误差如表2所列。

从图6～7和表2可以得出以下结论：

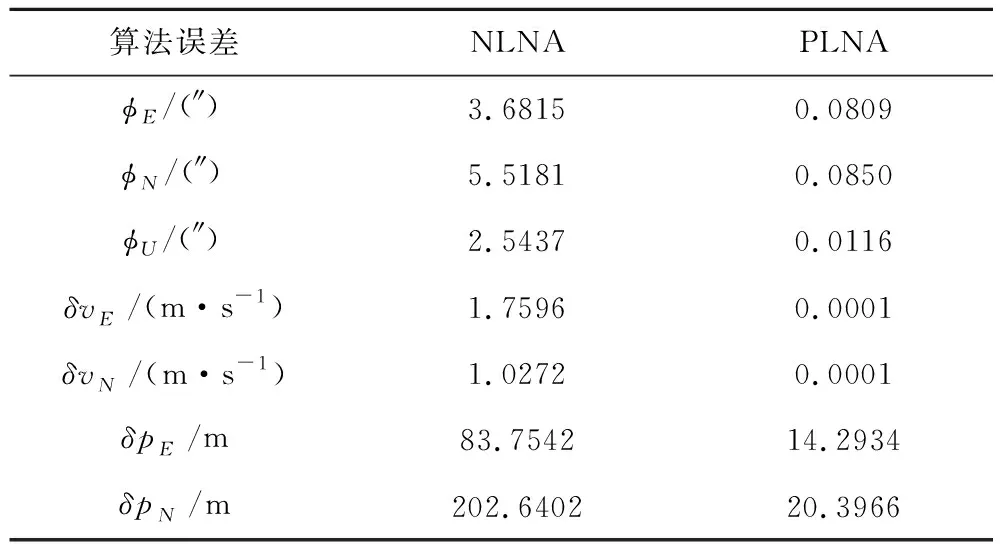
表2 旋转弹仿真算法误差Table 2 Algorithm errors in spinning projectile simulation

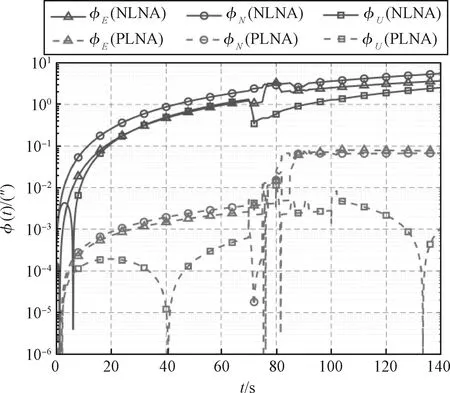
图6 旋转弹仿真姿态误差Fig.6 Attitude errors of spinning projectile simulation

(1)基于非线性模型的传统捷联惯导算法在大横滚角速度条件下算法误差远大于伪线性算法；

(2)从图7的位置误差变化图上可以看出，传统算法的位置误差在导航过程中一直发散，而伪线性导航算法的位置误差则在后半程基本不变，这说明伪线性算法在旋转弹导航中有明显的优势；

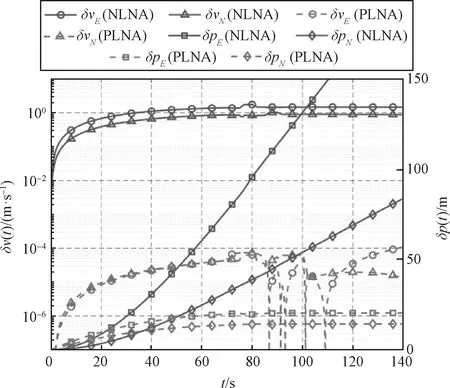
图7 旋转弹仿真速度与位置误差Fig.7 Velocity and position errors of spinning projectile simulation

(3)仿真结果表明，对于旋转弹,传统捷联惯导算法的算法误差已不能被忽略，因此捷联惯导算法误差模型不再准确，如果要进行组合导航，应当以伪线性捷联惯导算法为基础，建立组合导航系统线性状态空间模型。

4 结 论

本文在已有的高精度捷联惯导算法和伪线性系统理论的基础上，提出了完整的地理系下基于伪线性模型的捷联惯导算法。该算法可以求解线性系统方程实现捷联惯导解算更新，且在大机动条件下，例如有较大横滚角速度的旋转弹的导航解算中，有较高的算法精度。与传统的捷联惯导算法相比，基于伪线性模型的算法具有精度高、结构简单、线性化等优点，对于捷联惯导算法研究与工程应用有一定的参考价值。