不同深宽比矩形平面超高层建筑顺风向风致荷载的试验研究

陈伟兴,王奕可

(华南理工大学亚热带建筑科学国家重点实验室,广东 广州 510641)

超高层建筑是大城市重要的组成部分,也是未来建筑发展的趋势,其正朝着更高、更柔的方向发展。矩形平面的扁长板式超高层住宅建筑在此大背景下不断衍生而出,在经济发达地区其高度已逼近200 m,风荷载越来越成为板式超高层建筑结构安全性、舒适性和经济性的控制性荷载。在结构设计中发现,较小深宽比的板式超高层建筑起控制性作用的仍是顺风向风荷载;另一方面,凹角处理措施是影响结构顺风向气动荷载特性的主要因素之一,通过对结构外形进行优化设计可以有效降低顺风向风致荷载。因此,有必要在前期的结构设计阶段开展板式超高层住宅建筑的顺风向风致荷载随深宽比、凹角率等参数的变化规律的试验研究。

目前针对超高层建筑顺风向风致荷载的研究工作已日趋成熟,等效静力风荷载的概念及各类风致响应计算方法被诸多学者提出:Davenport[1]基于随机振动和抖振理论率先建立了计算高层建筑顺风向荷载的模型，并提出了风振响应的阵风荷载因子法(GLF)。此后国内外学者的研究工作都是在Davenport方法的基础上考虑一些其他参数所建立起来的,如我国《建筑结构荷载规范(GB 50009-2012)》现行版本所采用的惯性力法(IWL)[2],更好地反映了结构在脉动风作用下动力响应放大的物理本质;针对IWL法中背景响应仅用一阶振型计算的缺陷,Kasperski等[3]又提出了荷载响应相关法(LRC);而后美国Kareem等[4]和周印[5]在GLF法及IWF法的基础上,提出了基底弯矩阵风荷载因子法(MGLF)。而针对复杂的顺风向风致荷载问题,国内外风工程研究人员进行了大量的研究工作:唐意[6]对11个典型高层建筑刚性模型同步测压试验的基底力矩和三分力进行了研究,结果表明顺风向平均风荷载对D/B变化的敏感度大于顺风向脉动风荷载;熊勇等[7]等利用高频底座测力天平技术对67个矩形截面超高层建筑进行了风洞试验,发现宽厚比对整体阻力系数的影响非常显著,而平均风荷载对地面粗糙度的敏感度较小;张正维等[8]对2种不同凹角形式的典型方形截面高层建筑进行了风洞试验研究,结果表明7.5% 的凹角率能够最大程度地减小顺风向基底气动力系数。

已有研究主要存在的问题是:(1)整体体型系数作为评价顺风向风荷载的关键指标,缺乏较为系统的研究,且与《建筑结构荷载规范(GB 50009-2012)》的对比结果较少,有必要进一步评估规范相关参数的适用性;(2)流场湍流度是影响超高层建筑顺风向风荷载的一个极为关键指标,我国《建筑结构荷载规范》到GB 50009-2012版本才明确定义了不同地貌类型的湍流度分布[9]，且其值均不同程度地高于早期版本的隐含值,这也说明了早期的风洞试验低估了湍流度的影响;(3)由于模型制作方法、风场模拟精度及信号处理方式的差异,导致早期风洞试验对顺风向风致荷载的研究结果相对过于离散,从而导致风洞试验的离散性。

针对以上问题,华南理工大学风洞实验室团队采用高频底座测力天平技术,在严格按照GB 50009-2012[10]要求模拟出B、C两类风场的基础上开展了一系列28个模型工况详细风洞试验。本文主要介绍其中7种深宽比和3种凹角率的矩形平面超高层建筑模型的试验结果,分析了深宽比、湍流度、凹角率、结构周期和阻尼比对顺风向风致荷载的影响规律。

1 风洞试验概况

1.1 试验设备及风场模拟

试验在华南理工大学大气边界层风洞中进行,风洞试验段长24 m、宽5.4 m、高3 m,试验段后端配置4 m直径转盘,试验风速在0～30 m/s范围连续可调,测力试验采用高频底座测力天平(HFFB),通过安装在模型底部的高灵敏度天平测得结构在风荷载作用下的各基底力及倾覆弯矩。

试验在B、C两类地貌下进行,试验风场根据GB 50009-2012相关规定实施模拟,模拟出用于风洞试验的B类和C类两种地貌的风速比和湍流度，如图1所示。

图1 风速比和湍流度

1.2 试验模型制作及工况

为提高试验效率和模型精度,试验模型采用3D打印方式制作,通过预留的凹槽和扣件的相互拼接可以实现不同工况下的模型组合,这种制作组合方式可在一定程度上满足测力模型轻质高强的要求,试验模型如图2所示。

图2 试验模型照片

试验几何缩尺比为1∶400,建筑原型顶部高度均为200 m,对应风洞中模型顶部高度为0.5 m,高宽比为10,试验采样频率为 400 Hz,样本帧数为40 960,采样时间为102.4 s,试验风场共B、C两类地貌,每类地貌下共进行7种深宽比和3种凹角率工况的模型试验。试验风向角定义示意图如图3所示,以正东方向为 0°风向角,以顺时针方向进行 0°、15°、30°、45°、60°、75°、90°、180°、270°、345° 10个风向角的测试,B、D分别为迎风面特征宽度和深度。

图3 风向角定义示意图

1.3 原型结构动力特性及风场参数

数据分析所用的结构周期是基于已有工程经验和规范建议估计得到的,假定振型沿高度呈线性分布,结构质量为1 700 kg/m2,各深宽比工况前三阶模态自振周期见表1,相应阻尼比取5%,基本风压参照深圳市地区选取,其重现期100年和50年的基本风压分别为0.90 kPa和0.75 kPa。

表1 前三阶模态自振周期

2 数据处理及分析方法

2.1 数据预处理

试验中对测得的各基底力及倾覆弯矩多采用无量纲化的剪力系数和倾覆弯矩系数来表示,倾覆弯矩系数时程和剪力系数时程分别定义为

(1)

(2)

在采用HFFB试验时,由于天平和模型系统的耦合共振影响,导致由天平测取的是已经被天平模型系统放大了的弯矩信号,即“信号畸变”,必须加以修正[11]。采用文献[12]中的方法对被测信号进行修正,D/B=3工况0°风向角下基底气动弯矩功率谱密度的修正前后比较如图4所示。由图4可见,修正效果良好,整体上比较理想地解决了共振峰处信号畸变的修正问题,拓宽了信号的有效带宽。

图4 基底气动弯矩功率谱密度修正前后比较

2.2 结构风致荷载的计算方法

根据随机振动理论[13],将试验测得的基底气动弯矩功率谱密度SMA,x(f)(为简化描述以下统一用SMA(f)表示)乘以结构机械导纳|H(f)|2就可以得到修正后的基底气动弯矩功率谱密度SMD(f),即

SMD(f)=|H(f)|2SMA(f)，

(3)

|H(f)|2表达形式为

(4)

其中:f0、ζ分别为结构的一阶固有频率和模态阻尼比。对修正后的基底气动弯矩功率谱SMD(f)在全频域上进行积分再开方,便可得到基底弯矩响应均方根值σMD,即

(5)

在估算基底弯矩峰值响应时,可采用下式确定:

(6)

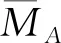
3 主要结果

3.1 整体体型系数

风荷载体型系数是指风作用在建筑物表面一定面积范围内所引起的平均压力(或吸力)与来流风的速度压的比值,主要与建筑本身的体型和尺寸有关。各个深宽比工况的整体体型系数随风向角的变化规律如图5所示。

图5 μx、μy随风向角变化曲线

由图5(a)可知,整体体型系数μx最大值出现在D/B=1处、0°风向角下,为-1.43,其绝对值略大于规范的整体体型系数最大值1.4,这个结果和一般认为正方形平面超高层建筑气动性能最差、风荷载最大的认知相符合。μx在0°风向角下为各深宽比工况窄边迎风时(D/B≥1)的整体体型系数,表现为顺风向,μx随D/B的增大显著减小,但并不是所有深宽比工况的μx最大值均出现在0°风向角,其余深宽比工况的μx最大值出现在15°或345°,且μx在0°和180°具有较好的一致性;μx在90°风向角下数据基本为0,原因是该风向角下表现为横风向,与270°具有较好的一致性。

由图5(b)可知,整体体型系数μy最大值出现在D/B=1.5及D/B=1处、90°风向角下,均为-1.5,其绝对值略大于规范的整体体型系数最大值1.4,μy在90°风向角下为各深宽比工况宽边迎风时(D/B<1)的整体体型系数,表现为顺风向,μy随D/B的增大逐渐增大,但增大幅度不大,且μy在90°和270°具有较好的一致性;μy在0°风向角下数据基本为0,原因是该风向角下表现为横风向,与180°具有较好的一致性。

早期的荷载规范版本并没有考虑深宽比参数变化对顺风向风致荷载的影响,GB 50009-2012版在续表8.3.1增加了有关体型系数的规定:针对高度超过45 m的矩形截面高层建筑,给出了不同深宽比D/B工况下背风面的体型系数,该条规定主要考虑D/B对矩形截面高层建筑背风面风荷载的影响,即背风面的体型系数绝对值随着截面深宽比的增大而减少。

将上述D/B≥1的整体体型系数μx和D/B<1的整体体型系数μy等试验数据绘于一起以便讨论其随深宽比的变化规律。各深宽比D/B工况的整体体型系数与荷载规范的对比结果如图6所示,图6中带圆点的平滑线即为荷载规范考虑迎风面和背风面叠加后的整体体型系数。由图6可见,D/B=0.67(D/B=1∶1.5)工况的μy绝对值达到最大值1.5(以下数据分析均基于绝对值讨论),在D/B<1时,μy随着D/B的增大逐渐增大,与规范预估的较小深宽比整体体型系数保持1.4不变的趋势有明显差异;在12.5后,μx风洞试验结果小于规范取值,风洞试验结果与规范取值呈现波动性交替领先,由此可见,规范在一定的深宽比范围内低估了结构的整体体型系数,有必要进一步深入研究深宽比对于顺风向风致荷载的影响规律。

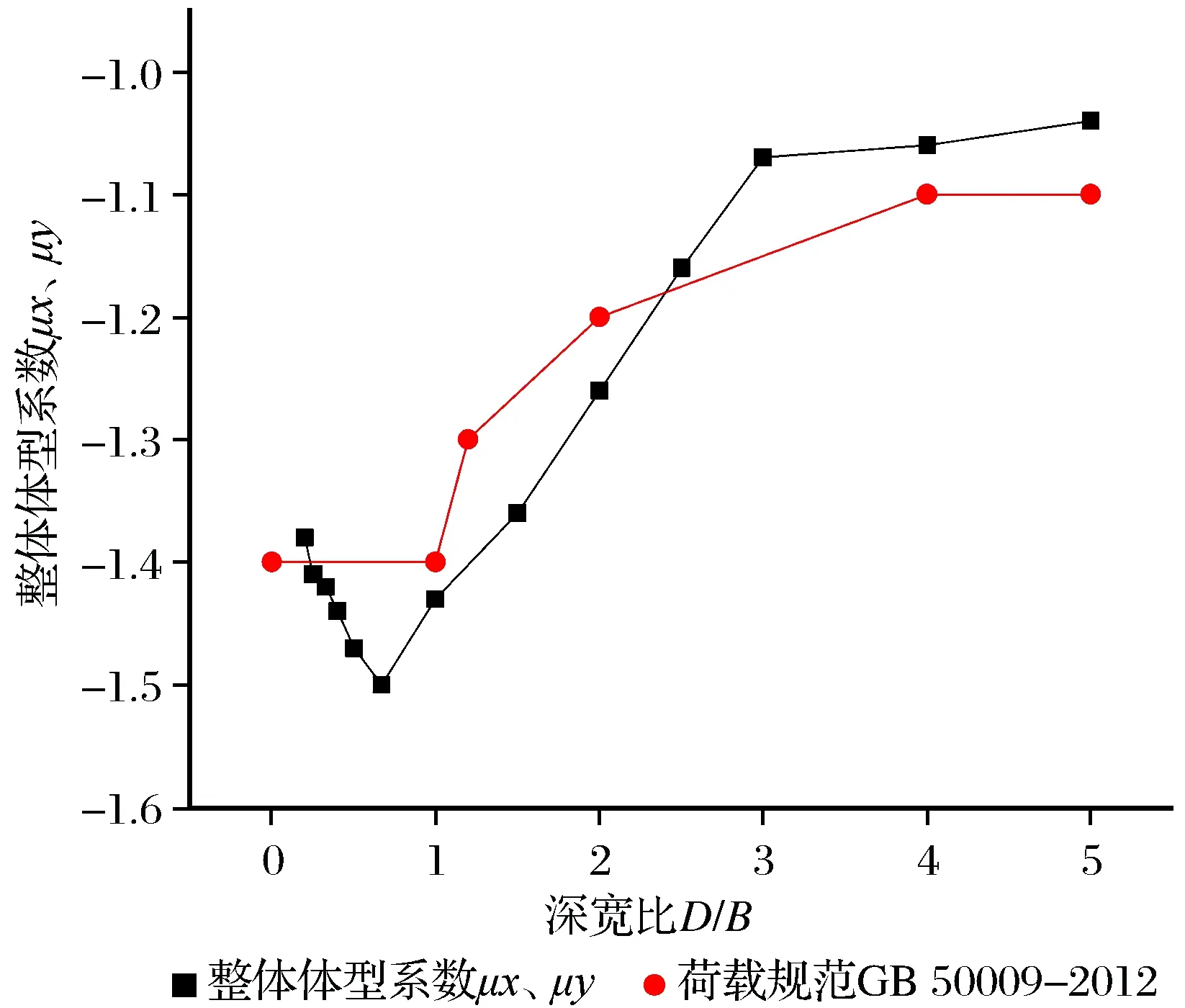
图6 μx,μy与规范的对比

3.2 深宽比的影响

图7 顺风向随深宽比变化曲线

表2 顺风向平均风荷载与横风向脉动风荷载对比

结合基底气动弯矩功率谱进一步说明顺风向风荷载随深宽比的变化规律。宽边迎风时(D/B<1)顺风向和横风向的基底气动弯矩功率谱如图8所示。 由图8(a)可知,顺风向基底气动弯矩功率谱没有明显的旋涡脱落峰值,高能量分布的频率范围较宽,具有明显的宽带特性，且随着深宽比D/B的增大,谱峰峰值频率向左移动,能量逐渐往低频集中,高频部分的功率谱密度值随着D/B的增大逐渐降低,顺风向风荷载逐渐不显著,与上节结论较为吻合。

图8 基底气动弯矩功率谱

对比图8(a)和图8(b),在深宽比D/B<0.5后,顺风向功率谱密度值最大值(10-1)明显大于横风向(10-2～10-3)的,两者差了一个数量级甚至更大,导致顺风向的风致荷载大于横风向的,更进一步说明顺风向在较小深宽比范围内起控制作用。

3.3 湍流度的影响

图9 B、C类风场下顺风向随深宽比变化

图10 D/B=2时顺风向基底气动弯矩功率谱

由图9可见:整体上B类地貌下的顺风向平均风荷载要高于C类地貌风场,B类地貌下的平均风荷载最大值约为C类地貌的1.67倍,出现在D/B=2工况下,两类地貌下的变化规律分布趋势相近,可见顺风向风荷载平均分量对湍流度变化较为敏感。结合图10的顺风向功率谱密度可见,D/B=2工况在B类风场下高频部分的功率谱密度值显著大于C类风场,B类风场下的顺风向风致荷载大于C类的。而针对顺风向脉动风荷载,B、C两类地貌下的数据情况较为相近,最大差异不超过23.8%,且随着深宽比D/B的增大,B、C两类地貌下的σMD偏差逐渐减小且两条曲线有重合的趋势，可见顺风向基底弯矩均方根值σMD对湍流度的敏感度随深宽比的增大逐渐减小，当深宽比D/B增大至5时,B、C地貌下的顺风向脉动分量偏差仅有3.7%。综上讨论，湍流度对顺风向脉动风荷载的影响程度小于顺风向平均风荷载。

3.4 凹角率的影响

图11 顺风向随凹角率变化

图12 D/B=3时凹角工况顺风向基底气动弯矩功率谱

顺风向基底弯矩均方根值σMD随着凹角率的增大先减小后增大,10%的凹角率下均为D/B=3、D/B=4的最优气动措施,且分别能降低23.73%和14.89%的顺风向脉动风荷载。

3.5 阻尼比的影响

结构模态阻尼比对顺风向风致荷载的影响主要体现在结构风致振动上,一定的结构阻尼能够耗散结构在风荷载作用下的振动能量。B类风场下50年重现期不同阻尼比的顺风向基底弯矩均方根值σMD随D/B的变化曲线如图13所示,阻尼比变化范围为0.01～0.05。

图13 不同阻尼比下σMD随深宽比变化

试验结果表明:随着阻尼比的减小,σMD明显提高,且σMD递增的幅度由小变大,当D/B=1∶1时,ξ=0.02的σMD比ξ=0.05的相应结果增大了32.49%,而在D/B=2下σMD的升幅更为显著。当ξ=0.02时,σMD为275.89 MN·m,比ξ=0.05的相应结果增大了35.37%,且其他阻尼比ξ=0.01、ξ=0.03、ξ=0.04的σMD较ξ=0.05工况分别增大了80.21%、16.78%、6.53%,偏差逐渐减小。这侧面反映了实际工程中利用准确的阻尼比计算结构风致荷载的重要意义,同时也说明了提高阻尼比有利于降低结构的顺风向风荷载,当阻尼比增大到一定程度时,顺风效应的这种减小作用趋于平缓。

4 结论

基于高频底座测力天平技术,对不同深宽比板式住宅超高层建筑进行了顺风向风致荷载的试验研究,从中得到以下结论:

(1) 在D/B<1时,μy随着D/B的增大逐渐增大,与规范GB J0009-2012里较小深宽比整体体型系数保持1.4不变的趋势有明显差异;在D/B>1后,μx与规范取值呈现波动性交替领先,规范在一定的深宽比范围内低估了结构的整体体型系数。

(2) 宽边迎风时的顺风向平均风荷载最大约为窄边迎风时的6.61倍,其对D/B的敏感度显著大于顺风向脉动风荷载,且顺风向平均风荷载在较小深宽比时起控制作用;B类地貌下的顺风向平均风荷载最大高出C类地貌66.7%,顺风向脉动风荷载对湍流的敏感度小于顺风向平均风荷载;D/B=3和D/B=4的最优凹角率分别为10%和15%,分别能降低23.76%和19.57%的顺风向平均风荷载,不同深宽比工况对不同凹角率处理的敏感性不同。

(3) 结构顺风向风荷载对阻尼比较为敏感,采用2%阻尼比的风荷载最大会比5%阻尼比的风荷载高出35.37%,在实际工程中利用准确的阻尼比计算结构风致荷载具有重要意义。