基坑开挖卸荷工程桩受力及变形特性分析

郑笠 陈琳 朱云 李镜培，*

基坑开挖卸荷工程桩受力及变形特性分析

郑笠1陈琳2朱云2李镜培1，*

（1.同济大学地下建筑与工程系，上海 200092； 2.上海南汇建工建设（集团）有限公司，上海 201399）

基坑开挖将引起坑底土体大面积回弹，带动坑内工程桩向上位移，改变桩土间受力状态。立柱桩上抬还将影响基坑的支撑体系，对基坑整体稳定性产生不利影响。本文基于桩弹性理论方法，充分考虑大面积基坑分步开挖卸荷、土体回弹对工程桩受力及变形的影响，采用残余应力法对土层回弹量进行计算，结合回弹量计算结果建立大面积基坑开挖工程桩位移和受力计算理论模型，分析桩顶荷载、基坑开挖深度以及桩长、桩径对桩侧摩阻力及桩土位移的影响，最后通过与工程监测数据对比验证结果的可靠性与合理性。计算分析结果表明，桩顶荷载、基坑开挖深度、桩长及桩径对桩侧摩阻力及桩土位移产生明显影响，随着基坑开挖深度增加桩侧将出现负摩阻力，可能引起桩身产生拉应力导致破坏。

工程桩， 土层回弹， 侧摩阻力， 基坑开挖

0 引 言

我国城市基础设施建设已经进入了全新的立体化开发与利用阶段，高层建筑以及地下工程不断涌现，与之相伴随的是超大面积基坑工程数量的显著增加［1］。深基坑施工具有土方开挖量大、暴露时间长、大面积开挖卸荷等特点，这将导致坑底土体明显回弹，在降低坑底抗隆起稳定性的同时，还将对已施工的工程桩的受力变形产生影响，甚至引起工程桩的破坏。许多工程实例表明，基坑开挖将对工程桩施加上拔力，桩身轴力将逐渐由受压向受拉状态转变［2］，随着开挖深度的增加上拔力逐渐加大，不仅可能使桩身开裂、拉断，并且对于支撑体系，上拔力及土体回弹引起的立柱桩的竖向位移将降低支护结构的稳定性。基于以上原因，需要针对深基坑开挖面积大、开挖深度深的特点，结合工程桩的受力特性，研究开挖卸荷过程中的桩-土相互作用机理，为定量分析土体回弹引起桩身的受力及位移的变化提供理论方法，具有一定的现实意义与理论价值。

深大基坑开挖对工程桩影响有主要有三个问题需要考虑：基坑回弹并作用于桩体的上拔作用，上拔引起桩身不同方向的侧摩阻力以及开挖导致桩侧土压力的降低［3］。目前在基坑开挖过程坑底土体的回弹计算方面已有较多研究，如潘林有等［4］通过对土样回弹路径特性进行深入的试验分析，提出了回弹区和强回弹区的范围，提出基坑卸荷回弹的估算公式。肖健［5］总结了基坑回弹量估算的方法，包括传统估算法、经验公式、残余应力法等，利用Abaqus有限元软件建立深基坑回弹计算的三维有限元模型，计算任意深度处的土体回弹量，定量地分析了基坑形状、基坑开挖面积以及开挖深度等空间因素对基坑开挖回弹量的影响。童星等［6］基于Mindlin应力解提出分层开挖条件下深大基坑底部土体卸荷附加应力计算方法，考虑了基坑开挖过程中土体回弹模量与附加应力的非线性关系，得出大部分深度范围内分层开挖下土体卸荷附加应力小于一次性开挖的结论。

在桩-土间相互作用机理及位移计算方面，目前常用的计算方法有荷载传递法、弹性理论法、剪切位移法及有限单元法。其中弹性理论法由D'Appolonia等［7］和Poulos等［8-11］先后提出并改进完善，该方法将桩周土视作匀质、连续、各向同性的线弹性无限半空间体，应用无限半空间体内点荷载作用下的Mindlin位移解求得荷载作用下桩的位移及受力。邹春华［12］对单桩弹性理论法进行改进，建立考虑桩土相对滑移时的单桩受力及位移的理论计算模型。操小兵等［2］基于剪切位移法建立了立柱桩位移的力学解析模型，结合立柱桩的实际边界条件提出了基坑开挖过程中立柱桩位移的计算方法。然而，目前将桩顶加载及基坑卸荷回弹两个过程相结合构建完整的桩-土作用机理的分析模型的相关理论研究较少，在土体回弹量计算方面也往往是采用分层总和法，没有考虑土体的弹塑性。

本文针对上海国际医学园区医药加速器（一期）项目大面积深基坑开挖工程，结合现场动态监测数据，以弹性理论法为基础，引入了开挖卸荷引起的土体回弹的作用，建立完整的桩身受力、位移的计算模型，在土层回弹计算方面应用残余应力法考虑土体的弹塑性对回弹量的影响，为工程设计中考虑桩身安全性及内支撑体系的稳定性提供理论依据。

1 土层回弹量计算

深基坑开挖往往伴随着显著的坑底回弹，本文采用Mindlin应力解计算开挖卸荷后土体内的应力变化。其中矩形均布荷载角点下土体竖向附加应力计算表达式为

式（1）为单一矩形均布荷载角点处附加应力的计算公式，通过不同矩形角点的组合则可以求解均布荷载作用下任意尺寸矩形基坑中任一点处下方附加应力分布，也可用于分区开挖施工的基坑。

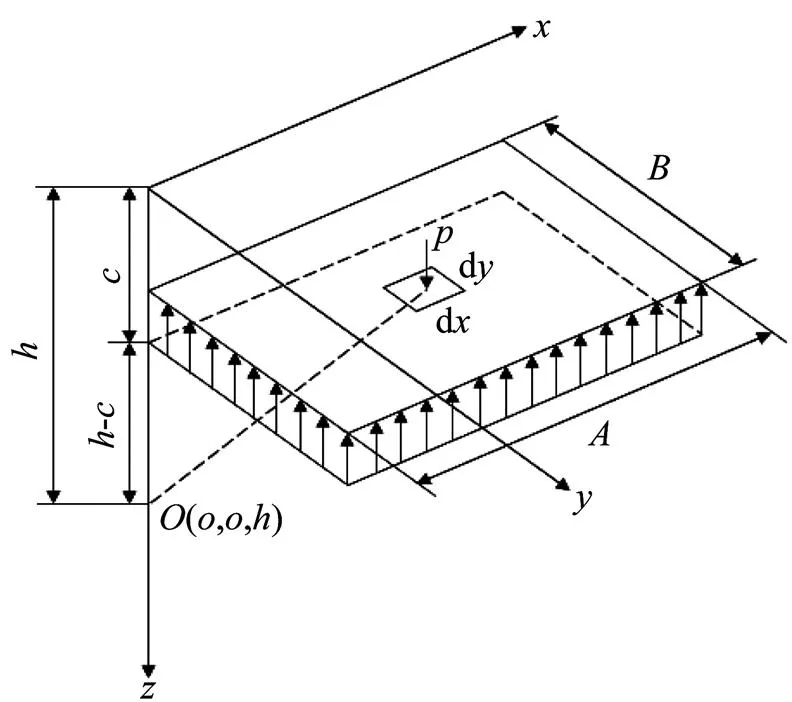
图1　矩形均布荷载计算模型

通过计算开挖面下任一点的残余应力值，便可利用积分形式的分层总和法计算坑底土体的回弹量：

图2　附加应力分布

图3　基坑土体回弹分布

2 考虑土体回弹的改进弹性理论法

2.1　传统弹性理论法

弹性理论法假定土体为理想均质各向同性的弹性半空间体，桩的存在不影响其弹性模量和泊松比。同时，桩周为粗糙面，能够在桩土间产生摩擦力，桩身的位移等于桩周土体的位移，桩底光滑与土体接触时相互挤压只产生压力。在计算中认为桩以及土体的径向位移较小，可以忽略不计，只计算桩和土体在桩顶荷载作用下的竖向位移［14］。

弹性理论法首先将桩及桩周土分解为若干单元，并将二者作为两个脱离体进行分析，其受力状态实际是作用力与反作用力的关系，通过桩身与桩周土的变形协调条件将二者结合，图4为桩土的受力状态分析。

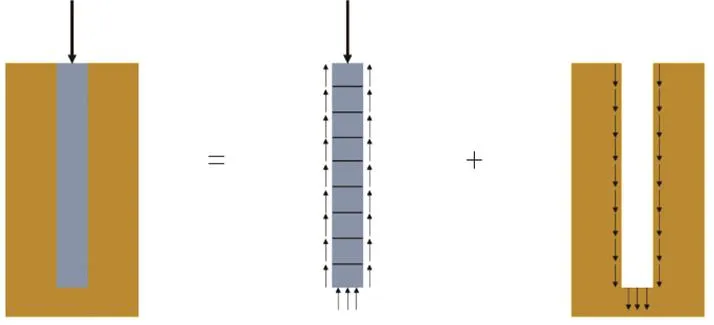
图4　弹性理论法计算模型

2.2　桩土位移方程

式中：为单元j处的单位摩阻力引起桩段i处竖向位移值，称为竖向位移影响系数；为桩底单位荷载引起桩段i处的竖向位移，其计算方法可参考文献［14］，本文不再赘述；为单元j处的侧摩阻力；为桩底反力；为土层的弹性模量。

由此可得土层的位移方程：

如图6所示为桩身计算模型，弹性桩受力变形微分方程为［14］

式中：为桩侧摩阻力；为桩身弹性模量；为桩身位移。

通过将上式改写为有限差分展开形式，并引入桩顶的位移条件，可以得到整根桩的位移方程为［14］

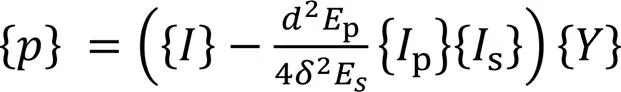
通过式（10）可以计算得到桩周摩阻力以及桩底反力，再分别带入式（7）或式（9）可以计算得出桩土位移。

2.3　考虑土体回弹的改进弹性理论法

杨敏等［15］认为土体回弹时土体位移与桩身位移间有如下关系：

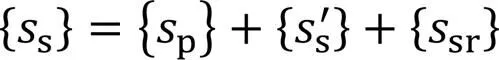
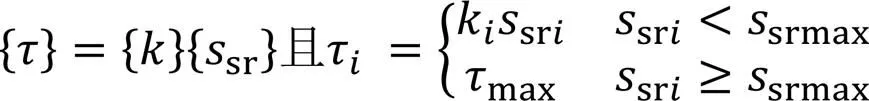
假定不考虑桩身自重及桩端土体作用力的变化，桩身摩阻力在变化后应受力平衡，即：

将式（7）、式（13）带入式（12）可以得到土体回弹后的桩土相对位移如式（15）所示，进而再将桩土相对位移带入式（13）计算回弹引起侧摩阻力的变化：

2.4　计算方法及步骤

采用上述考虑土体回弹的改进理论计算方法计算，桩土受力、位移的步骤如下：

按下式计算［12］：

3 开挖卸荷对工程桩受力变形的影响规律分析

根据第三章改进计算步骤对基坑开挖过程中桩土受力、位移情况进行分析计算并总结相关规律，通过改变桩顶荷载、基坑开挖深度及工程桩桩长、桩径取值讨论加载条件、基坑开挖参数及桩的几何参数对桩身侧摩阻力、桩土位移的影响。在第四章各节中若对某一参数无特殊说明，该参数值按表1所示取值。

表1　 参数分析基本取值

3.1　桩顶荷载影响

本节主要探讨不同桩顶荷载作用下，桩身侧摩阻力及桩土位移的变化情况，除桩顶荷载外其余参数取值按照表1选取。图7为不同桩顶荷载作用下桩侧摩阻力的变化情况，桩侧摩阻力向上为正。从图7中可以看出桩侧摩阻力沿深度的分布有三段：首先第一段是桩顶开始的一定深度内，桩侧摩阻力始终达到极限摩阻力值，该深度随着桩顶荷载增加而增加，并且由于桩侧极限摩阻力随着上覆土层压力增大而增大，因此桩侧摩阻力也随深度逐渐增大；随后到达第二段，该段桩侧摩阻力沿深度逐渐减小，由于本节分析中考虑了基坑开挖深度为5 m，工程桩发生回弹，因此在桩顶荷载较小时（=2 000 kN、4 000 kN），桩侧摩阻力减小过程中出现负摩阻力；第三段则出现在桩底附近，当桩顶荷载较小时桩底附近负摩阻力进一步减小，当桩顶荷载较大时正摩阻力数值在桩底附近则略微回升。

图7　桩顶荷载对桩侧摩阻力的影响

图8表示桩顶荷载作用下工程桩和土层的位移情况。其中图8（a）为土层位移，图8（b）为桩身位移，位移向下为正。从图8（a）可以看到，由于基坑开挖将引起土层回弹，在桩顶荷载较小时，土层位移沿深度分布基本都为负值，随着桩顶荷载的增加，土层位移整体将逐步下沉，对于图8（b）的桩身位移也呈现类似的规律，桩身位移沿着深度方向是逐渐减小的，说明桩身整体压缩。同时两图中曲线中均存在明显转折点，转折处出现在图7侧摩阻力第二段起始深度附近。

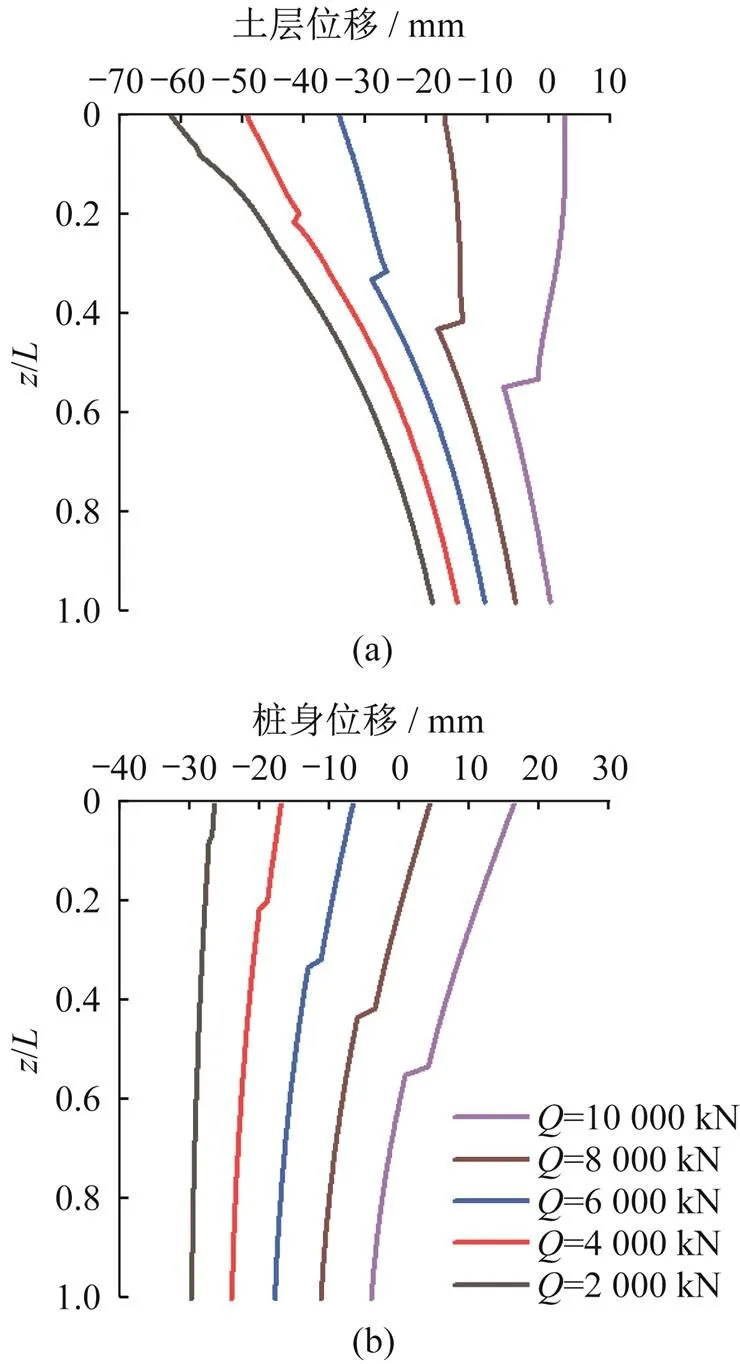
图8　桩顶荷载对桩土位移的影响

3.2　基坑开挖深度影响

随着基坑开挖坑底土体及工程桩将发生明显回弹，进而改变桩侧摩阻力的大小与分布情况。本节主要探讨不同开挖深度，桩身侧摩阻力及桩土位移的变化情况，除基坑开挖深度外其余参数取值按照表1选取。

图9表示不同开挖深度下桩侧摩阻力沿桩身的分布情况，图10则表示不同开挖深度下桩土位移情况，桩顶荷载取2 000 kN。从图9、图10中可以看到，基坑未开挖时（=0 m），桩侧摩阻力沿深度均为正值，桩土位移则均为正，即桩下沉。随着开挖深度的增加，土层回弹逐渐增大，同时也牵引工程桩向上回弹，此时桩身上段摩阻力增大，下段桩侧摩阻力为了平衡上段增大的摩阻力，其值逐渐减小，并逐渐转变为负摩阻力。开挖深度越大，则桩的摩阻力绝对值越大，并且由于桩身中出现负摩阻力，随着开挖深度的增加，桩身将可能出现较大的拉应力，导致桩身受拉破坏。

图9　基坑开挖深度对桩侧摩阻力的影响

图10　基坑开挖深度对桩土位移的影响

3.3　桩长径及桩径的影响

本节主要探讨不同桩长和桩径下桩身侧摩阻力及桩土位移的变化情况，其中为桩长为桩径，其余参数取值按照表1选取。

图11和图12分别表示不同工程桩桩长对桩侧摩阻力和桩土位移的影响。图11显示随着桩长的增加，桩侧摩阻力曲线的绝对值明显增加，即负摩阻力和正摩阻力部分均是增大的。从图12（a）看到不同桩长下土层位移沿桩身的分布情况有所不同。在沿桩身0.2倍桩长深度范围内，桩长较长的桩土层回弹较桩长较短的桩更大，随着相对深度/的增加土层位移明显减小，桩身下段的土层回弹量相比桩长短的桩则会更小。图12（b）则表示桩身整体上抬位移随着桩长增加而逐渐减小。

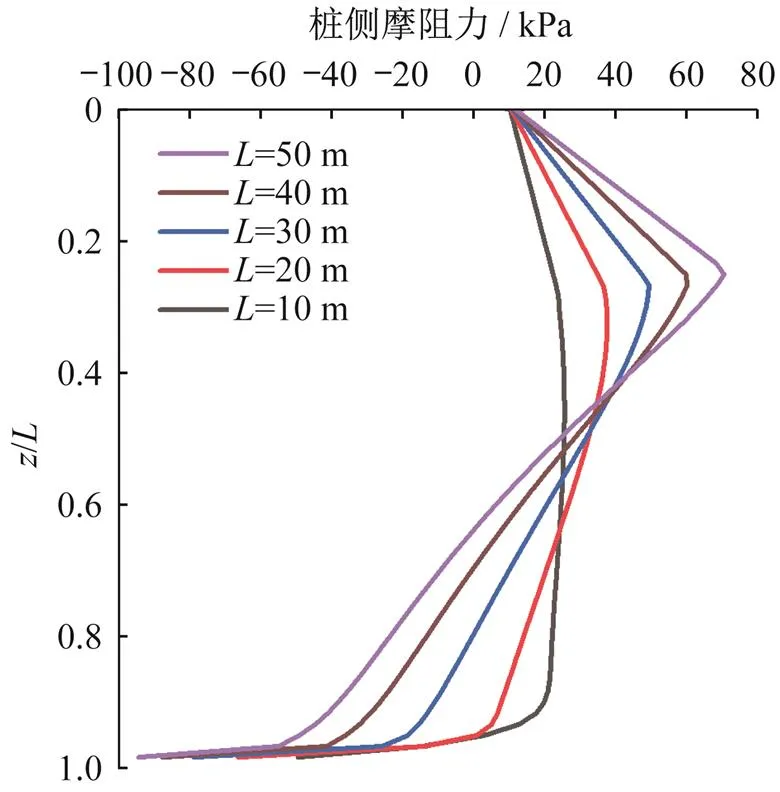
图11　桩长对桩侧摩阻力影响

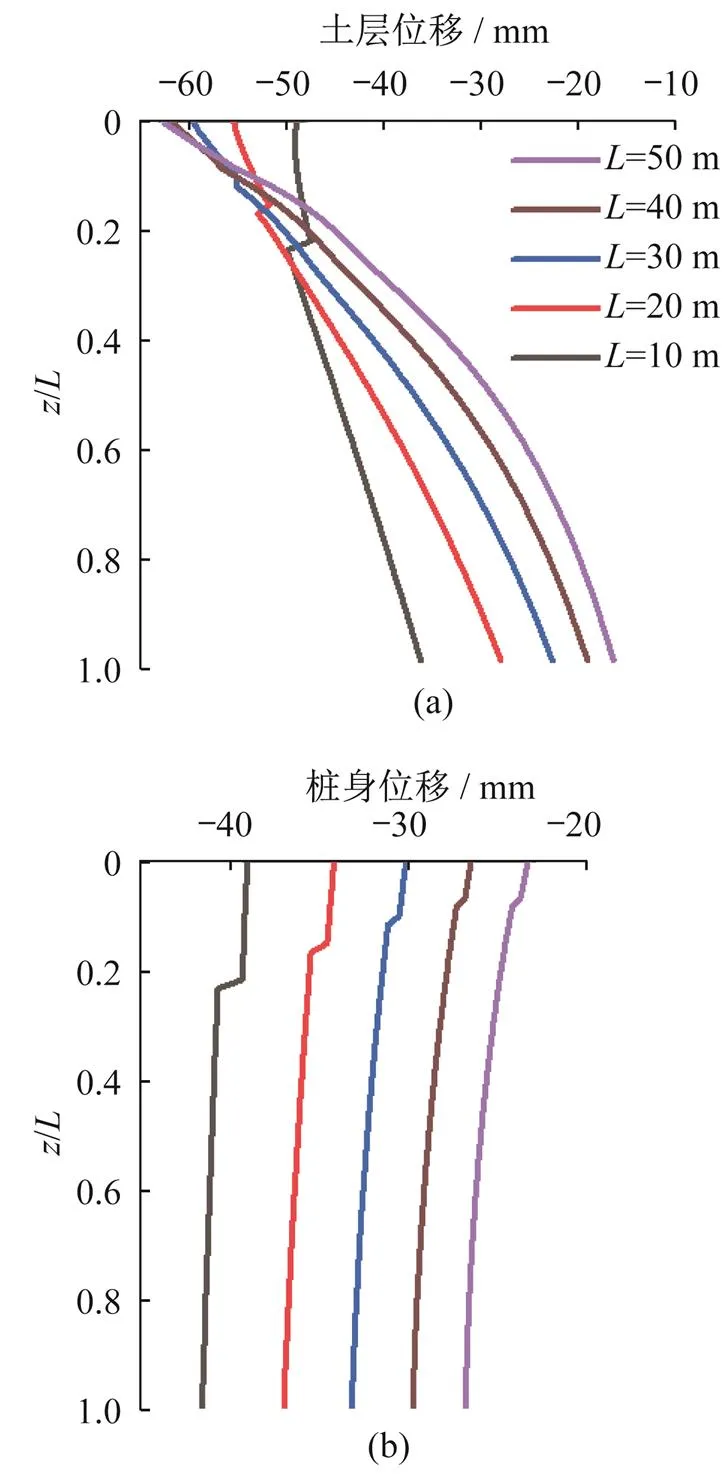
图12　桩长对桩土位移的影响

图13和图14表示不同工程桩桩径对桩侧摩阻力和桩土位移的影响。从图13整体可以观察到，与桩长的变化规律不同，桩侧正摩阻力随着桩径的增加而减小，这是由于随着桩径的增加桩土接触面积更大由于基坑开挖引起反方向的桩土间侧摩阻力，使桩身下半段正摩阻力减小，由于桩径大的桩正摩阻力值较小，因此其负摩阻力值相比桩径小的桩会更大，但从斜率上看桩径大的桩侧摩阻力减小趋势更缓慢。图14则显示随着桩径增加土层及桩身回弹整体均逐渐增加。

图13　桩径对桩侧摩阻力影响

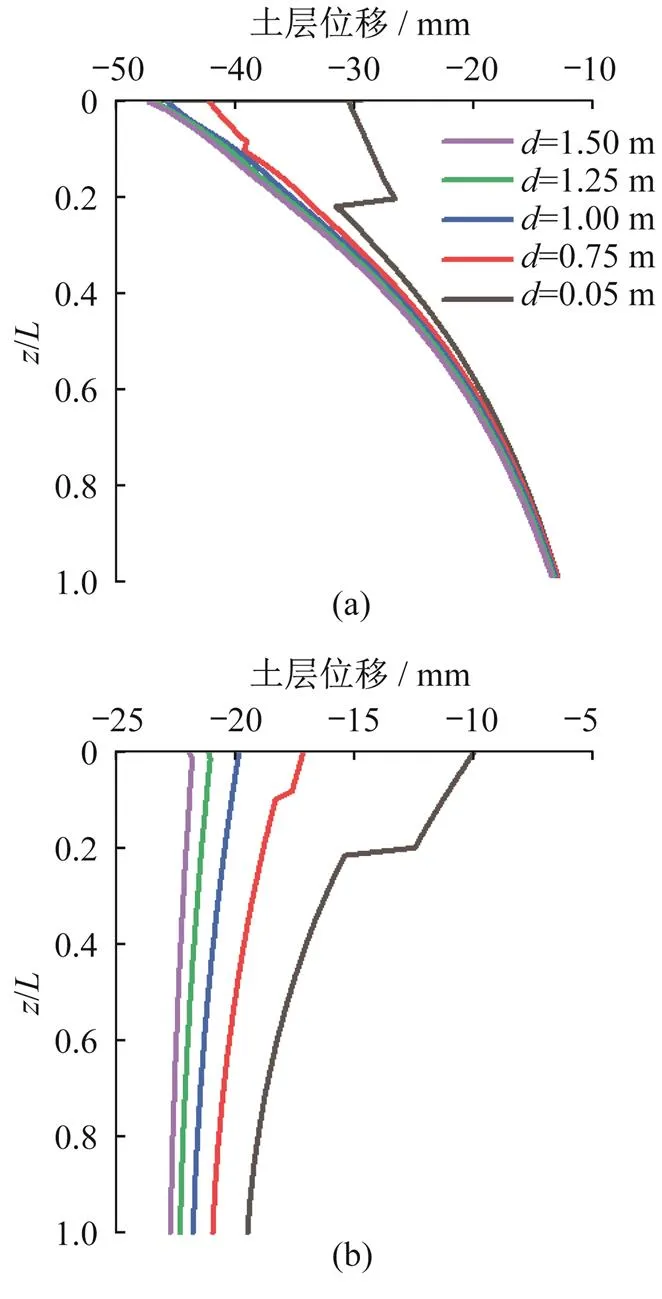
图14　桩径对桩土位移的影响

3.4　结果对比

图15　桩侧摩阻力计算结果对比

4 工程实例计算

上海国际医学园区医药加速器（一期）项目位于上海市浦东新区，场地东至康新公路，南至五灶港，西至景观纵三河，北至紫萍路。该基坑总面积达32 242 m2，总延长米为899 m。根据基坑的面积、开挖深度及功能分区，将基坑划分为A、B两个区域，其中，A区基坑位于西北角，包含能源站及部分一层地下室，基坑开挖深度11.85 m，基坑面积3 329 m2，延长米约232 m，坑内立柱桩桩长26 m，桩径为1.0 m；B区基坑主要为一层地下室，开挖深度6.2 m，基坑面积28 913 m2，延长米约667 m，基坑施工开挖将在较深的A区基坑和超大面积的B区基坑相继展开。监测单位提供的监测数据包括A区立柱桩水平及垂直位移、围护墙顶位移、深层水平位移、坑外潜水水位、周边地表沉降、管线位移、支撑轴力等，本文A区立柱桩在开挖过程中的垂直位移，基坑形状其相关监测点布置如图16、图17所示，图17中L为立柱桩位移监测位点，共6处。A区主要土层的参数如表2所示（不考虑杂填土），计算参数取计算深度范围内平均值，回弹模量根据参考文献中经验值选取［16］。

表2　 场地土层参数

注：*表示的数值为根据经验，按土体压缩模量的3倍估算得到［16］。

图16　基坑形状及周边监测点

图17　A区监测位点

A区基坑分两次开挖，第一次开挖深度为6.8 m，第二次开挖深度为5.05 m，基坑详细施工工况如表3所示。

表3 施工工况

Tab.3　 Construction state

图18显示了监测记录点L1和L3的桩顶回弹位移监测值与理论计算值的对比及相对误差，计算过程中将图17中A区简化为矩形以左上角为原点，基坑边为、轴，基坑尺寸为54 m×64 m，测点L1座坐标为（10.05，10.05），L3坐标为（10.05，32）。图18（a）为L1和L3测点监测值与计算值的对比图，从图中可以看到，随着基坑开挖深度增加，两测点桩顶回弹量也逐步增加，L1相比L3更靠近基坑角点，因此回弹量较小，计算值与监测值在数值和变化趋势上较为一致。图18（b）则为两监测点监测值与计算值间的相对误差，按式（18）计算。图中显示相对误差在-5%～16%，误差较小，因此本文方法也可以较为合理预测该工程桩顶位移变化。

5 结 论

本文基于传统弹性理论法，结合基坑开挖土体回弹变形对弹性理论法进行改进，建立基坑开挖卸荷工程桩受力及变形特性分析模型，并针对不同施工参数，如桩顶荷载、开挖深度、桩长、桩径等因素进行影响规律分析，主要结论如下：

（1） 桩侧摩阻力沿桩身分布为三段，第一段桩侧摩阻力沿深度增加，第二段为侧摩阻力明显减小，第三段出现在桩底附近，桩侧摩阻力出现略微转折。

（2） 桩顶荷载、基坑开挖深度、桩长及桩径对工程桩侧摩阻力分布、桩土位移均有显著影响，尤其是在基坑开挖过程中，土层回弹将牵引工程桩向上回弹，使桩身上部将出现负摩阻力，并随着开挖深度的增加逐渐增大，并可能出现较大的拉应力，导致桩身破坏。

（3） 通过将本文计算结果与现有研究成果及工程实例进行对比，验证了本文分析模型的合理性，能够较好预测基坑开挖过程中工程桩受力及位移情况，为实际设计和施工过程提供参考。

［1］黄茂松，王卫东，郑刚.软土地下工程与深基坑研究进展［J］.土木工程学报，2012，45（6）：146-161.

Huang Maosong，Wang Weidong，Zheng Gang.Research progress of soft soil underground engineering and deep foundation pit［J］.Chinese Journal of Civil Engineering，2012，45（6）：146-161.（in Chinese）

［2］操小兵，金文，李镜培，等.基坑开挖卸荷引起立柱桩的隆起位移计算［J］.结构工程师，2018，34（1）：131-137.

Cao Xiaobing，Jin Wen，Li Jingpei，et al.Calculation of uplift displacement of soldier Piles Caused by Unloading of excavation.Structural Engineers，2018，34（1）：131-137.（in Chinese）

［3］郑刚，刁钰，吴宏伟.超深开挖对单桩的竖向荷载传递及沉降的影响机理有限元分析［J］.岩土工程学报，2009，31（6）：837-845.

Zheng Gang，Diao Yu，Wu Hongwei.Finite element analysis on mechanism of effect of extra-deep excavation on vertical load transfer and settlement of a single pile［J］.Chinese Journal of Geotechnical Engineering，2009，31（6）：837-845.（in Chinese）

［4］潘林有，胡中雄.深基坑卸荷回弹问题的研究［J］.岩土工程学报，2002（1）：101-104.

Pan Linyou，Hu Zhongxiong.Chinese Journal of Geotechnical Engineering，2002（1）：101-104.（in Chinese）

［5］肖健.考虑工程桩存在的深基坑回弹空间效应有限元分析［D］.天津：天津大学，2004.

Xiao Jian.FEM analysis on 3D behavior of the pit resilience considering foundation piles［D］.Tianjin：Tianjin University，2004.（in Chinese）

［6］童星，袁静，姜叶翔，等.基于Mindlin解的基坑分层卸荷附加应力计算及回弹变形的多因素影响分析［J］.岩土力学，2020，41（7）：2432-2440.

Tong Xing，Yuan Jing，Jiang Yexiang，et al.Calculation of layered unloading additional stress based on Mindlin solution and multi-factor analysis of rebound deformation of a foundation pit［J］.Rock and Soil Mechanics，2020，41（7）：2432-2440.（in Chinese）

［7］ D'Appolonia E，Romuaidi J P.Load transfer in end-bearing steel h-piles［J］.Journal of the Soil Mechanics and Foundations Division，1963，89（2）：1-25.

［8］ Poulos H G，Stewart D P，Loganathan N.Centrifuge model testing of tunnelling-induced ground and pile deformations［J］.Géotechnique，2000，50（3）：283-294.

［9］ Poulos H G.Analysis of the settlement of pile groups［J］.Géotechnique，1968，18（5）：449-471.

［10］ Poulos H G.Settlement of single piles in nonhomogeneous soil［J］.Journal of The Geotechnical Engineering Division，1979，105：627-641.

［11］ Poulos H G，Davis E H.Pile foundation analysis and design： New York：Wiley，1980，397P［J］.International Journal of Rock Mechanics and Mining ences and Geomechanics Abstracts，1981，18（5）：100.

［12］邹春华.单桩计算的弹性理论法及其改进［D］.成都：西南交通大学，2007.

Zou Chunhua.Improvement on elastic theory method for single pile［D］.Chengdu：Southwest Jiaotong University，2007.（in Chinese）

［13］李德宁，楼晓明，杨敏.基坑回弹变形计算方法研究及应用［J］.岩石力学与工程学报，2012，31（9）：1921-1927.

Li Dening，Lou Xiaoming，Yang Min.Research and application of calculation methods for rebound deformation of foundation pits［J］.Journal of Rock Mechanics and Engineering，2012，31（9）：1921-1927.（in Chinese）

［14］朱百里.计算土力学［M］.上海：上海科学技术出版社，1990.

Zhu Baili.Computational soil mechanics［M］.Shanghai：Shanghai Science and Technology Press，1990.（in Chinese）

［15］杨敏，逯建栋.深开挖基坑回弹引起的坑中桩受力与位移计算［J］.同济大学学报（自然科学版），2010，38（12）：1730-1735.

Yang Min，Lu Jiandong.Calculation of force and displacement of pile in pit caused by springback of deep excavation［J］.Journal of Tongji University （Natural Science Edition），2010，38（12）：1730-1735.（in Chinese）

［16］楼晓明，杨晶，李德宁，等.立柱桩在深基坑分步开挖过程中的上拔位移分析［J］.岩土工程学报，2013，35（1）：193-198.

Lou Xiaoming，Yang Jing，Li Dening，et al.Uplift displacement of soldier piles during stepped excavation of deep foundation pits［J］.Journal of Geotechnical Engineering，2013，35（1）：193-198.（in Chinese）

Analysis of Stress and Deformation Characteristics of Piles in Foundation Pit Excavation

ZHENGLi1CHENLin2ZHUYun2LIJingpei1，*

（1.Department of Geotechnical Engineering，Tongji University， Shanghai 200092， China； 2.Shanghai Nanhui Construction Group Co.， Ltd.， Shanghai 201399， China）

Foundation pit excavation causes a large area of soil rebound at the bottom of the pit， leading to an upward displacement of engineering piles and change the lateral frictional stress between piles and soil. The lifting of pillar piles also affects the supporting system of the foundation pit and has a negative impact on the overall stability of the foundation pit. Based on the classical elasticity theory method, the effects of large foundation pit excavation in stages and soil rebound on the stress and deformation of engineering piles are fully considered in this paper. Residual stress method is used to calculate the soil rebound, and a theoretical model is established for the calculation and analysis of displacement and stress of engineering piles in large excavations. The effects of pile top load， foundation pit excavation depth， pile length and pile diameter on lateral friction stress and pile/soil displacement are analyzed. Finally， the reliability and rationality of the results are verified by comparing with the engineering monitoring data.The calculation and analysis results show that the pile top load， excavation depth，pile length and pile diameter have significant effects on the lateral frictional stress and pile/soil displacement.With the increase of excavation depth，there will be negative frictional resistance between pile and soil layer,which may cause tensile stress in the pile body and lead to its failure.

engineering pile， soil rebound， lateral friction stress， foundation pit excavation

2021-06-08

上海市浦东新区城建系统科学技术研究项目（PCKY202005）

郑 笠（1996-），男，硕士研究生。E-mail：1932330@tongji.edu.cn

联系作者：李镜培（1963-），男，教授，博士生导师，从事桩基础和岩土工程可靠度等研究。E-mail：lijp2773@tongji.edu.cn