钢筋UHPC梁抗弯承载能力理论分析
杨丙文 张建东
钢筋UHPC梁抗弯承载能力理论分析
杨丙文1,*张建东2
(1.南京交通职业技术学院,南京 211188; 2.南京工业大学土木工程学院,南京 211816)
根据受弯构件正截面承载力计算的原理,假定钢筋UHPC梁受弯时满足平截面假定、材料的本构关系为双折线、梁受拉区考虑部分抗拉强度,将受压区UHPC截面简化成矩形受力面和三角形受力面之和,将受拉区UHPC截面简化成矩形受力面,推导出钢筋UHPC梁在受弯时受压区的合力公式及合力的作用点公式,进而得出钢筋UHPC梁抗弯承载能力理论计算方法,利用该计算方法对已有的钢筋UHPC抗弯试验梁进行分析,并与试验得到的抗弯极限结果对比,结果表明,利用所推导的理论计算方法对钢筋UHPC抗弯承载能力的计算具有较高的精度,并利用推导公式对UHPC梁的配筋率和含纤维量对抗弯承载力进行分析,得出它们对抗弯承载力的影响。
超高性能混凝土, 抗拉强度, 抗弯能力, 极限承载力
0 引 言
超高性能混凝土(UHPC)应用于工程中具有高强度、高韧性、高耐久性和减轻结构自重等优点,超高性能混凝土的应用可以减少水泥用量和混凝土成型对大气的污染,随着工艺的不断成熟和价格的不断降低,在建筑工程结构中具有较广阔的应用前景[1]。目前UHPC在桥梁建设[2]、建筑外墙材料、作为加固材料等多方面已得到研究和应用[3]。在桥梁建设方面[4],欧洲已超过18座已建UHPC桥梁;在北美洲据统计也已达200多座;亚洲的马来西亚已有100多座UHPC桥梁建成的实例,韩国利用UHPC材料建成具有代表意义的Super Bridge I和LEGO斜拉桥,并正在开展更大跨径斜拉桥的设计研究,中国湖南大学的邵旭东教授团队[5]也已提出“超大跨径单向预应力UHPC连续箱梁桥概念设计”,随着社会的不断发展和技术的不断进步,UHPC在建筑工程结构中的应用越来越广泛。
对于有关UHPC的制备[6]、材料性能[7-9]、分类方式[10]、结构等性能[11-12],目前各国学者也相继做了大量试验[13]和理论研究,在UHPC构件的可靠性[14]、抗弯性能[15-19]、抗剪性能[20]、结构设计[12,21]、模拟计算[22]等多方面都取得了丰硕的成果。
关于UHPC的应力应变关系[23-26],学者们通过大量实验,给出了受拉和受压的关系式,从关系式可以看出,在极限应变范围内,UHPC的应力应变关系可近似看作双折线关系。在钢筋UHPC梁的抗弯性能方面[15-19],一些学者[13]通过试验已证明,采用等效矩形压应力分布,且不考虑UHPC的抗拉强度的普通混凝土结构抗弯设计方法不适用于UHPC梁的设计,会使计算结果偏小。一些学者[15-16]在此基础上,依然将受压区等效成矩形截面,受拉区同样等效成矩形截面,通过试验与理论相结合提取其修正系数,但不同的学者其等效应力的修正系数不尽相同;还有一种方法[23,25]是将受压区等效成三角形,认为UHPC的应力应变关系是线性关系,这与材料的本构关系存在差异性。本文根据UHPC的本构关系特点,将受压区等效成矩形加三角形,受拉区简化成矩形截面,对钢筋UHPC梁抗弯承载力进行分析,推导思路遵守结构设计原理,计算结果较吻合试验结果,产生的误差满足工程建设要求。
1 理论分析
1.1 基本理论
根据中国北京交通大学余自若教授团队[12]相关试验推导的UHPC的本构关系式可知,在UHPC未达到峰值应力对应的应变前,应力与应变的关系接近于线性变化(图1),为计算方便,可近似看做双直线:

式中:;;为混凝土峰值应力对应的应变;为混凝土峰值应力。
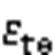

图2 UHPC梁受弯应力、应变分布及简化计算形式

图3 UHPC理想受拉应力-应变关系
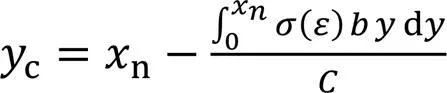
将式(3)积分计算后得:

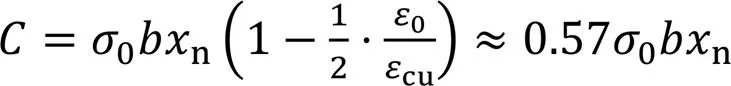
1.2 矩形截面梁
根据受弯构件正截面承载能力计算的基本原理,可以得到单筋矩形截面受弯构件承载力计算简图(图4)。

图4 单筋矩形截面受弯构件正截面承载力计算图示
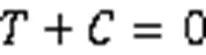
央广网经济之声《天下财经》报道称,张译找到吴浈,称其公司在药品审评中遭到不公待遇,希望国家食药监总局对其疫苗进行复检,被吴浈拒绝。

根据平截面假定和上述定义,当处于超筋梁界限时,满足式(9):
1.3 T形截面梁


图5 T形截面
故根据平衡条件得到基本计算公式为
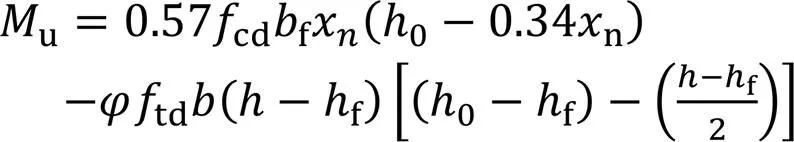
2 试验结果对比
文献[16]中,邓宗才教授团队做了根T形截面钢筋UHPC梁的抗弯性能试验。该试验选用的UHPC材料其棱柱体轴心抗压强度为115.1 MPa,棱柱体轴心拉伸试验测得的抗拉强度平均值为5.6 MPa;采用钢筋为φ16的超强钢筋,其钢筋屈服强度为518.3 MPa;采用钢筋为φ18的超强钢筋,其钢筋屈服强度为535.7 MPa;矩形梁最外层钢筋保护层厚度为18 mm;T形梁最外层钢筋保护层厚度为19 mm。矩形梁截面尺寸为150 mm×200 mm,钢筋布置如图6(a)—(d)所示;T形梁截面尺寸及布筋如图6(e)所示。试验梁的抗弯承载能力试验结果与本文理论结果对比见表1。

图6 试验梁截面配筋图(单位:mm)
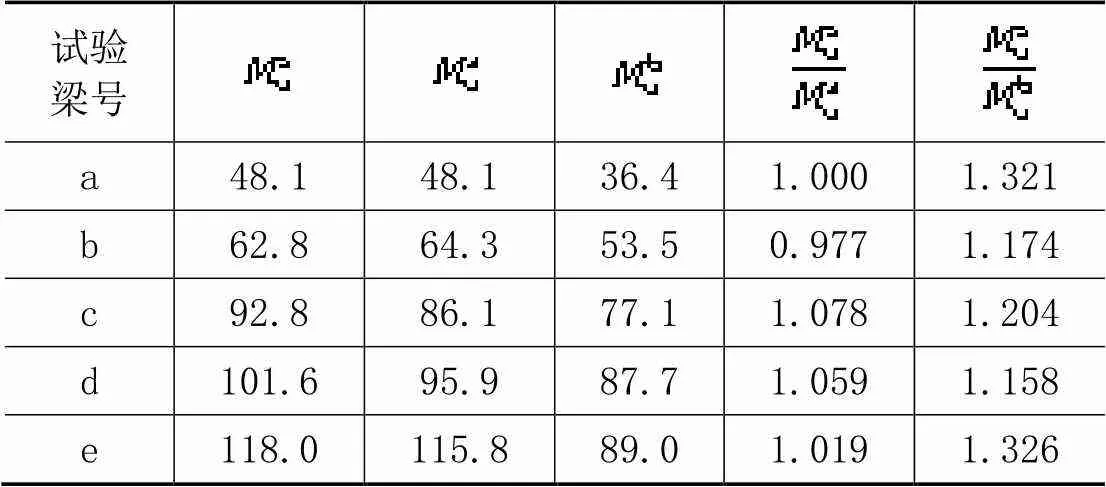
表1 试验结果与本文计算结果对比
由表1可以看出:该理论计算的抗弯承载力与试验结果较接近,最大偏差不大于8%,且理论计算值小于试验值,符合设计偏安全考虑的原则;当按照普通钢筋混凝土受弯结构分析(不考虑混凝土的抗拉强度),所求的抗力小于试验值,但误差较大,最大误差达32%,以该方法设计计算势必会浪费材料。
3 参数分析
3.1 配筋率对抗弯承载力影响
利用本文理论解,对UHPC梁中配筋率对抗弯承载能力的影响做分析,选择图5中矩形梁,UHPC及钢筋材料的性质如上,钢筋形心距底边缘距离为18 mm,根据不同的配筋率,其结果如表2及图7所示。

表2 配筋率变化对抗弯承载能力影响

图7 抗弯承载能力随着配筋率的变化图
根据表2和图7可以得出:随着配筋率的增大,其UHPC梁的抗弯承载能力基本呈线性增加,且增加得较为明显,当配筋率增加2倍时承载力增加1.63倍,当配筋率增加3倍时承载力增加2.21倍,说明在UHPC梁中,其抗弯承载能力依然取决于受拉区钢筋的配置数量及钢筋的屈服强度。
3.2 UHPC中纤维含量对抗弯承载力影响
在UHPC材料中,随着掺入的纤维量的不同,其抗拉强度标准值也不相同,以模型a为例,在不同的钢纤维含量下,其对应的抗弯承载力如表3和图8所示,对于无纤维含量的UHPC梁,由于受拉区无高应变强化,故其抗拉强度标准值取0。
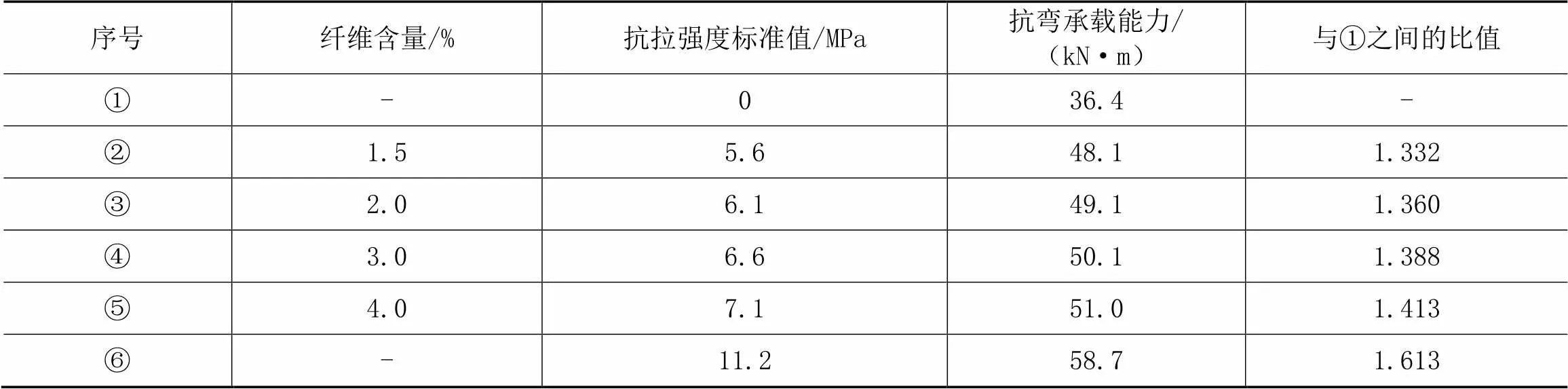
表3 纤维含量变化对抗弯承载能力影响

图8 抗弯承载能力随着纤维含量(抗拉强度)的变化
从表3和图8中可以看出:同种材料,随着纤维含量的增加,其抗拉强度随之增加使结构的抗弯承载力亦增加,但增加不明显(相对钢筋截面的增加),从钢纤维含量1.5%增加到3.0%,即钢纤维含量增加1倍,而抗弯承载力才增加5.7%,然而当抗拉强度从5.6 MPa增加1倍至11.2 MPa,抗弯承载力增加了将近30%,其UHPC材料的抗拉强度也是提高抗弯承载力的主要部分。
4 结 论
通过以上分析可以得出以下结论:
(1) 根据UHPC的性能及本构关系,提出钢筋UHPC梁抗弯承载力理论计算的简化模式。
(2) 根据超筋梁定义和第二类T形梁定义,分析出钢筋UHPC梁一般不会产生超筋梁现象;不会产生第二类T形梁结构。
(3) 推导钢筋UHPC梁的受压区合力及合力的作用点公式,进而得出矩形截面和T形截面钢筋UHPC梁抗弯承载能力理论计算方法。
(4) 利用本文推导的理论公式,对受拉区钢筋的配筋率进行参数分析,得出钢筋的配筋量依然是UHPC梁抗弯承载力的主要标志。
(5) 通过多纤维含量的参数分析得出,UHPC的抗拉强度有一定的提高抗弯承载力作用,但当纤维含量变化对抗拉强度影响不大时,对提高抗弯承载力作用较小。
[1] Aydin S,Baradan B.Engineering properties of reactive powder concrete without portland cement[J].ACI Materials Journal,2013,110(6):619-627.
[2] Chen B C,Huang Q W,Shen X J,et al.Two pilot UHPFRC bridges in China[J].ACF Magazine,2015,1(2):42-47.
[3]陈宝春,韦建刚,苏家战,等.超高性能混凝土应用进展[J].建筑科学与工程学报,2019,36(2):14-24.
Chen Baochun,Wei Jiangang,Su Jiazhan,et al.Application progress of super high performance concrete[J].Journal of Building Science and Engineering,2019,36(2):14-24.(in Chinese)
[4]陈宝春,季韬,黄卿维,等.超高性能混凝土研究综述[J].建筑科学与工程学报,2014,31(3):1-24.
Chen Baochun,Ji Tao,Huang Qingwei,et al.Summary of research on super high performance concrete[J].Journal of Building Science and Engineering,2014,31(3):1-24.(in Chinese)
[5]邵旭东,詹豪,雷薇,等.超大跨径单向预应力UHPC连续箱梁桥概念设计与初步实验[J].土木工程学报,2013(8):91-97.
Shao Xudong,Zhan Hao,Lei Wei,et al.Conceptual design and preliminary experiment of super long span prestressed UHPC continuous box girder bridge[J].Journal of Civil Engineering,2013(8):91-97.(in Chinese)
[6] Richard P,Cheyrezy M.Composition of reactive powder concrete [J].Cement and Concrete Research,1995,25(7):1501-1511.
[7] Kang S T,Lee K S,Choi J II.Control of tensile behavior of ultra-high performance concrete through artificial flaws and fiber hy-bridization[J].Concrete Structures and Materials,2016,10(3):33-41
[8] Wille K,Tavwil S,Naaman A E.Properties of strain hardening ultra-high performance fiber reinforced concrete (UHP-FRC) under direct tensile loading[J].Cem Concr Compos,2014,48:58.
[9] Makia T,Bruhwiler E.Tensile fatigue behavior of ultra-high performance fibre reinforced concrete[J].Materials and Sturctures,2013,47(3):475-491.
[10] Naaman A E,Reinhardt H W.Proposed classification of HPFRC composites based on their tensile response[J].Materials and Structures,2006,39(5):547-555.
[11] Yoo D Y,Yoon Y S.Structural performance of ultra-high-performance concrete beams with different steel fibers[J].Engineering Structures,2015,102:409-423.
[12]马啸.UHPC肋板结构力学性能研究[D].北京:北京交通大学,2018.
Ma Xiao.Study on mechanical properties of UHPC rib structure[D].Beijing:Beijing Jiaotong University,2018.(in Chinese)
[13]袁娜.活性粉末混凝土预应力T梁的设计、试验及正截面承载力的研究[D].北京:北京交通大学,2004.
Yuan Na.Design,test and research on bearing capacity of normal section of prestressed T-beam of reactive powder concrete[D].Beijing:Beijing Jiaotong University,2004.(in Chinese)
[14] Eric S.Structure reliability of prestressed UHPC flexure models for bridge girders[J].Journal of Bridge Engineering,2010,15(1):65-72.
[15]曹霞,常婧,王艳俊.高强钢筋RPC梁受弯构件正截面承载力试验研究[J].河南理工大学学报(自然科学版),2015,34(1):109-116.
Cao Xia,Chang Jing,Wang Yanjun.Experimental study on bearing capacity of flexural members of high strength reinforced RPC beams[J].Journal of Henan University of Technology (Natural Science Edition),2015,34(1):109-116.(in Chinese)
[16]邓宗才,王义超.高强钢筋UHPC梁抗弯性能试验研究与理论分析[J].应用基础与工程科学学报,2015,23(1):68-78.
Deng Zongcai,Wang Yichao.Experimental study and theoretical analysis on flexural behavior of UHPC beams with high strength reinforcement[J].Journal of Applied Foundation and Engineering Science,2015,23(1):68-78.(in Chinese)
[17] Graybeal B.Flexural behavior of ultrahigh-performance concrete I-girder[J].Journal of Bridge Engineering,2008,13(6):602-610.
[18] Ahmood M,Dawood M.Flexural behavior of continuous bubbled reinforced reactive powder concrete flat slab[J].Journal of Babylon University,2017,25(2):504-505.
[19] Yang I H,Joh C,Kim B S.Structural behavior of ultra high performance concrete beams subjected to bending[J].Engineering Sturctures,2010,32:3478-3487.
[20]康佩.活性粉末混凝土构件在受弯、受剪、受压状态下的设计计算方法[D].北京:北京交通大学,2012.
Kang Pei.Design and calculation method of reactive powder concrete members under bending,shearing and compression[D].Beijing:Beijing Jiaotong University,2012.(in Chinese)
[21] Zhang G,Graybeal B A.Development of UHPC pi-girder sections for span length up to 41 m[J].Journal of Bridge Engineering,2015,20(3):1-8.
[22] Chen L,Graybeal B A.Modeling structural performance of ultrahigh performance concrete I-girders[J].Journal of Bridge Engineering,2012,17:754-764.
[23]杜任远.活性粉末混凝土梁、拱极限承载力研究[D].福州:福州大学,2014.
Du Renyuan.Study on the ultimate bearing capacity of reactive powder concrete beam and arch[D].Fuzhou:Fuzhou University,2014.
[24] Graybeal B A.Characterization of the behavior of ultra-high performance concrete[D].Maryland:University of Maryland,2005.
[25] U.S.Department of transportation federal highway administration.design guide for precast UHPC waffle deck panel system,including coimections[S].America,2013.
[26] Wille K,Tavwil S,Naaman A E.Properties of strain hardening ultra high performance fiber reinforced concrete (UHP-FRC) under direct tensile loading[J].Cem Concr Compos,2014,48:58.
[27]刘超,黄钰豪,马汝杰,等.高应变强化超高性能混凝土T形梁抗弯承载力[J].同济大学学报(自然科学版),2018,46(6):744-750.
Liu Chao,Huang Yuhao,Ma Rujie,et al.Calculation method for flexural capacity of high strain-hardening UHPC T-beams[J].Journal of Tongji University (Natural Science Edition),2018,46(6):744-750.(in Chinese)
[28]范昕.大比例预应力UHPC-T形梁抗弯性能试验研究[D].长沙:湖南大学,2017.
Fan Xin.Testing and modeling flexural behavior of a large-scale prestressed UHPC T-beam[D].Changsha:Hunan University,2017.(in Chinese)
Theoretical Analysis of Bending Capacity of Reinforcement UHPC Beams
YANG Bingwen1,*ZHANG Jiandong2
(1.Nanjing Communications Institute of Technology, Nanjing 211188, China; 2.College of Civil Engineering Nanjing Tech University, Nanjing 211816, China)
According to the principle of calculation of the bearing capacity of the normal section of a flexural member,it is assumed that the reinforced UHPC beam meets the assumption of a flat section when bending, the material constitutive relationship is a double-fold line, and the tensile strength of the beam takes the partial tensile strength into account. The section is simplified into the sum of rectangular force surface and triangle force surface. The UHPC section in the tension zone is simplified into a rectangular force surface. The formula of the combined force and the point of action of the combined force in the compression zone of the reinforced UHPC beam during bending are derived. Furthermore,a theoretical calculation method for the flexural bearing existing reinforced UHPC beams is obtained.This calculation method is used to analyze the existing reinforced UHPC flexural test beams, and the results are compared with the obtained bending limit results. The results show that the deduced theoretical calculation method is the calculation of the UHPC flexural bearing capacity of steel bars has a high accuracy,and the derivation formula is used to analyze the reinforcement ratio and fiber content of the UHPC beam to resist the bending capacity, and the influence of their resistance to the bending capacity is obtained.
ultra-high performance concrete, tensile strength, resistance moment, ultimate bearing capacity
2021-02-26
国家自然科学基金项目(51778288)
联系作者:中文作者简介:杨丙文(1983-),男,博士,高级工程师,主要从事组合结构研究。E-mail: ybw0904@126.com

