某体育馆上盖张弦梁设计

金汉

某体育馆上盖张弦梁设计

金汉*

（北京市建筑设计研究院有限公司，北京 100045）

某体育馆平面尺寸为69.2 m×21.0 m，为满足建筑效果，在21.0 m跨度方向布置15榀单向张弦梁，本文主要运用两种软件进行分析，其中整体分析采用MIDAS GEN，节点分析采用ABAQUS，主要从如下4个方面对张弦梁进行计算论证保证安全：①根据平衡态寻找初拉力；②由于建筑功能原因，张弦梁上弦较平，会产生较大的水平推力，本文通过调整施工顺序分析解决造型产生的推力及水平变形；③通过线性及非线性屈曲分析计算上弦稳定性；④支座处复杂节点材料非线性分析。通过以上4个方面计算保证项目安全可靠，可为类似张弦梁结构的设计提供参考。

初拉力， 施工阶段模拟， 屈曲分析， 节点分析

0 引 言

随着科技的快速发展，人们追求美观建筑的需求日益强烈，解决大跨方案的结构形式也越来越多，如桁架、钢骨混凝土梁、网架、张弦结构等。本文就某体育场馆上盖单向张弦梁结构进行分析论证，保证其安全性。

1 工程概况

某体育馆位于北京市某高校高精尖实验室楼旁的地下一层顶，层高为9.6 m。平面长×宽为69.2 m×21.0 m，结构平面布置图如图1所示，其中序号1—8为张弦梁，跨度为21.0 m，序号0为普通钢梁。建筑剖面为图2，根据上弦杆抛物线形状分为8种；张弦梁典型剖面见图3，其中1～8榀中间撑杆高度不变，变化图中的a与b值及上弦杆的标高，形成8榀不一样的单向张弦梁。

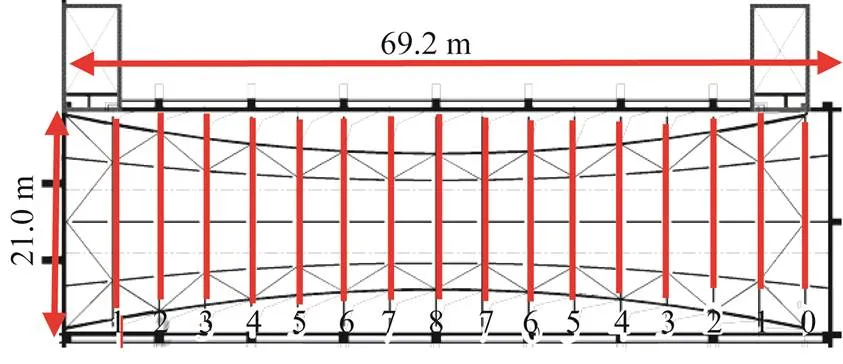
图1　结构平面布置图

图2　剖面图

图3　张弦梁剖面图

本工程跨度为21.0 m，可选方案有预应力混凝土梁，钢骨混凝土梁，桁架形式等。由于工程位于教学楼旁边的地下体育馆，建筑专业为展现学校的科研能力，契合高精尖的主题气质，要求馆内结构效果要轻巧。桁架方案室内效果凌乱，而混凝土方案则笨重而毫无新意，几经对比，本工程最后选择了张弦梁方案。

主要杆件截面：GL1为箱形，700（高）×400（宽）×12（腹板）×30（下翼缘）×60（上翼缘）；材料为Q345C。

CG1为圆杆：P245×16（壁厚）；材料为Q345C。

SUO为索，截面：φ5×187；材料：1670级；整体结构模型见图4。

图4　结构计算模型图

2 计算论证

2.1　初始张拉力的确定

张弦结构由上弦杆、撑杆、下弦索三部分组成，其形态优美轻巧，通过对索的张拉，使其产生轴向拉力，通过力的分解，索轴力对撑杆作用向上的反力，撑杆再把反力传给上弦杆［1］，这时三者形成一个稳定静定结构，且刚度随着张拉力的提高而增大，上弦钢梁的截面高度得以准确控制以获得更高的室内空间和更好的视觉效果。由于建筑专业对空间品质和效果的把控，往往不能以结构最合理的曲线来设计张弦结构，而是需要和建筑方案设计的最理想的抛物线形态相结合。结构专业能做的就是根据调整初始张拉力来使已定的张弦结构最合理［2］。

张弦梁结构由于索的力学性能可分为：①零状态；②初始态；③荷载态。［3］

零状态——结构不承受任何预拉力和外荷载的作用时的状态。

初始态——预拉力与自重共同作用的工作状态。

荷载态——结构在初始状态的基础上，考虑其他各种工作荷载时的情况。

张弦梁索的初始拉力的确定，可由式（1）反求得出。

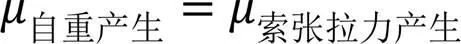
用MIDAS GEN建立模型，其中张弦梁两端按铰接，按式（1）计算，汇总索初始拉力结果于图5。

图5　张弦梁编号-索轴力柱状图

根据图5可以发现索的轴力大小不均。分析原因是1～8榀上弦的形态，1～8榀抛物线作用越来越强，其中1榀上弦杆形态接近直线。上弦杆形态抛物线作用越强，下弦索的作用越明显，内力越大。

2.2　施工模拟

确定索初拉力后，对整体张弦梁施加使用荷载，其中恒载为16 kN/m²，活载为5 kN/m²。

施加完使用荷载后，查看正常使用状态下即D+L工况的变形，上弦挠度达到86 mm，为1/244，略大于《钢结构设计标准》［4］中的1/250。经分析，因为上盖800 mm厚的覆土，造成了恒荷载过大，可以通过增大初始拉力来解决问题。本文通过调整初始张拉力（图6），加上施工起拱，满足钢结构规范中挠度1/250要求。

图6　张弦梁编号-索轴力柱状图

在正常使用情况下，上盖结构上的地面为供人行走的室外场地，故张弦梁上弦需要是水平直线，而不能选择最常见的抛物线形式，水平上弦最大的难题是会对支座产生较大的推力。

根据荷载组合1.3（+pre）+1.5，统计各榀推力x（沿索方向），如图7所示。

图7　张弦梁编号-支座反力柱状图

从图7可知，所有榀的水平推力都达到一个较高的数值，其中最小的有1 500 kN，最大的则高达4 500 kN，对于4 500 kN这样的高数值，预埋件和抗剪键组合的节点无法满足设计要求。如果通过支座形式例如椭圆孔或是球铰支座来释放水平变形，计算发现（图8）沿着索方向变形达到118 mm，较大的水平变形造成节点的构造复杂。如果采用球铰节点，会产生如下几个影响：①与球铰相连的牛腿为满足变形要求，造型会很大，不能满足建筑效果；②球铰构造缝隙需相关专业想办法解决；③本工程又位于地下室顶盖，水平缝隙带来的防水问题不好解决；④过大的变形还会使得次构件安装产生误差。

图8　张弦梁编号-水平位移（延索方向）曲线图

displacement （cable direction）

本文尝试通过改变施工顺序来解决水平位移过大带来的影响，施工顺序如下：

（1） 根据初始拉力在地面按100%张拉力进行张拉，此时张拉端锚固件相当于仅约束竖向变形的铰接支座；

（2） 吊装至屋面，一端铰接，一端滑动（释放水平延索方向约束），组装张弦梁平面外次梁，水平支撑；

（3） 加使用荷载。

本文采用MIDAS GEN对上述施工步骤进行模拟，得出施工各个步骤每榀张弦梁的水平位移如图9所示，其中正为沿着索，负为背离索；图10为最终使用阶段（步骤3）各榀张弦梁的下弦索的内力。

图9　张弦梁编号-水平位移（延索方向）曲线图2

图 10　张弦梁编号-索轴力柱状图2

分析得出最终使用阶段（步骤3）最后的综合水平位移仅为12 mm此时水平推力为0 kN，支座可采用常见的椭圆孔设计，且变形满足建筑效果要求。因此通过调整施工顺序可有效降低释放水平位移带来的影响。

图10为最终使用阶段索内力，可以发现各榀张弦梁的索内力趋于平均，最大为2 210 kN，最小为2 050 kN。相差不大，可以按2 210 kN来设计耳板节点。

2.3　屈曲分析[5]

2.3.1线性屈曲分析

张弦梁结构是由上弦杆，撑杆以及索共同组成，在使用阶段上弦杆为压弯构件，撑杆为轴心受压构件，索为受拉构件，其上弦杆及撑杆往往有稳定问题。目前主流分析复杂钢结构稳定性的方法为屈曲分析［6］。

对结构进行屈曲分析，引入公式：

图11　第7榀第一阶屈曲模态

2.3.2非线性屈曲分析

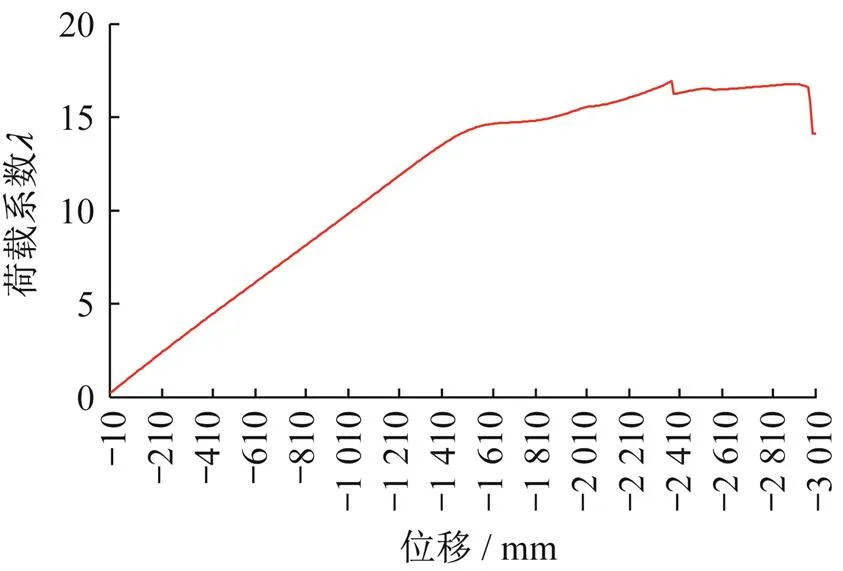
图12　节点1位移-荷载系数曲线

2.4　节点分析

张弦梁根部节点构造较为复杂，根据公式计算往往不能准确反映实际情况，本文借助ABAQUS软件对根部节点进行1∶1实体模型分析，其中杆件分为三个部分：① 60 mm竖向支撑；② 钢梁（上弦杆GL5）；③ 耳板（60 mm厚），此三部分均采用实体单元（Solid）［8］，如图13与图14所示。

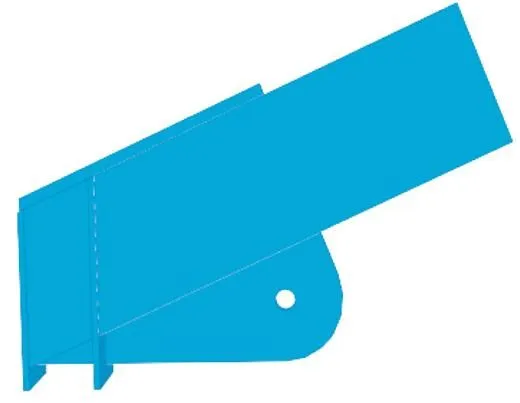
图14　ABAQUS模型简图

2.4.1本构模型[9]

考虑钢材材料非线性，采用规范一般定义：钢结构采用二折线本构模型，材料为Q345，弹性模量2.06×105N/mm2，泊松比0.30，塑性应变为0，屈服应力345 N/mm2。

2.4.2边界条件、接触、荷载及网格划分

钢梁与耳板，耳板与竖向支撑实际是坡口焊，在模型中互相接触的面采用绑定（tie），耳板周圈面耦合到圆心点，提取8榀中在荷载组合下最大的索轴力=2 210 kN，施加在耳板圆心点上。

提取钢梁上的力：

F=-1.8 kN，F=213.8 kN，F=-2076 kN，

x=-316.3 kN·m，y=2.8 kN·m，z=0 kN·m施加在钢梁端部，如图15所示；竖向支撑底部采用铰接，释放水平向约束；网格划分见图16，实体单元均采用C3D8R单元。

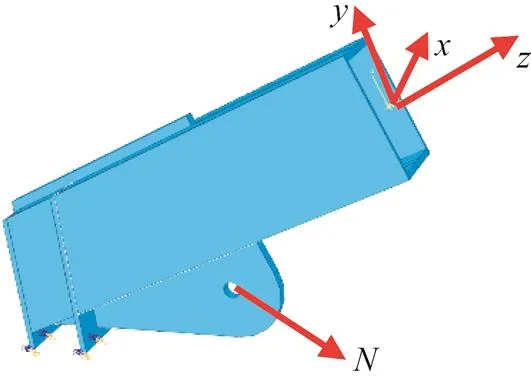
图15　边界条件及荷载

图16　网格划分

2.4.3计算结果

由图17～图20可知，各个部件均未达到屈服，其中竖向支撑最大应力值为283 MPa<345 MPa，耳板最大应力值为294 MPa<345 MPa，钢梁最大应力值为329 MPa<345 MPa，节点设计满足要求。

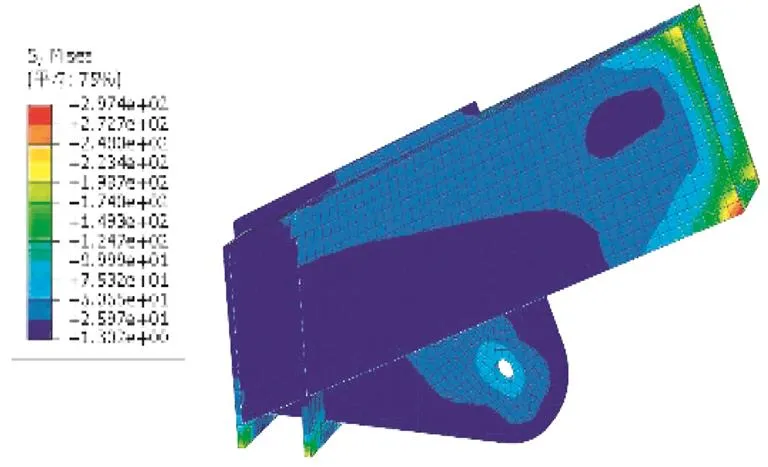
图17　整体模型应力图

图18　竖向支撑应力图

图19　耳板应力图

图 20　水平钢梁应力图

CG1撑杆为轴向受压杆件，经计算CG1稳定应力比最大为0.436。为保证撑杆为轴向受压状态，并保证索的内力有效传到撑杆，本工程采用图21的节点，索内力通过索夹传给4根高强螺栓，由4根对称的高强螺栓传给纵向加劲肋，由2块对称的纵向加劲肋传给撑杆。对称的高强螺栓及竖向加劲肋保证了荷载的有效传递。

图 21　下撑杆轴测图

3 结 论

（1） 给出索初始拉力的确定方法，一般受荷较小的张弦梁初始拉力可根据自重产生的挠度与张拉力产生的挠度平衡反求出初始张拉力。如果受荷较大，可通过加大前一步确定的初始张拉力，逐步找到最优解。

（2） 张弦梁结构往往通过找形可达到自平衡状态，但是如果上弦较“平”，为水平直线，形态原因会产生较大水平推力，推力过大会造成节点设计困难。可通过释放水平约束，对推力释放，释放推力产生的变形可通过施工模拟分析得到控制。本工程通过调整施工顺序，最大水平变形由118 mm下降到12 mm，让根部节点得以实现。

（3） 张弦梁结构上弦杆为压弯构件，需重点注意稳定性问题，线性屈曲分析往往偏于不安全；本文通过线性屈曲分析以及考虑初始缺陷非线性屈曲分析两种情况分别计算荷载系数，得出加载需达到使用荷载的16.29倍结构才会发生失稳，满足设计要求。

（4） 张弦梁根部节点设计往往 “非”常规，可借助有限元手段对节点进行实体模型模拟，本工程节点中竖向支撑、耳板、水平钢梁在最不利工况作用下，应力均未达到钢材屈服值，满足设计要求。为保证CG1撑杆为轴向受压，本工程通过设置对称的高强锚栓及竖向加劲肋有效保证了索内力的传递。

本文通过详细的步骤对张弦梁结构进行了分析计算，可对类似工程做参考。

［1］赵佩峰.张弦梁结构的受力性能分析［D］.合肥：合肥工业大学，2005.

Zhao Peifeng.The Internal Force of The Beam String Structure Alysized by Ansys［D］.Hefei：Hefei University of Technology，2005.（in Chinese）

［2］吴捷.基于平衡荷载态整体优化的双向张弦梁弹塑性极限承载力参数分析［J］.钢结构，2019，34（2）：9-14.

Wu Jie.Analysis of parameters affecting elastoplastic ultimate capacity of bidirectional beam string structure after total optimization based on balanced load state［J］.Steel Construction，2019，34（2）：9-14.（in Chinese）

［3］［3］秦明.张弦梁结构在midas Gen中的应用［J］.特种结构，2018，35（5）：68-72.

Qin Ming.Application of beam string structure in midas gen［J］.Special Structures，2018，35（5）：68-72.（in Chinese）

［4］ GB 50017—2017 钢结构设计标准［S］.北京：中国建筑工业出版社，2017.

GB 50017—2017 Standard for design of steel structures［S］.Beijing：China Architecture & Building Press，2017.（in Chinese）

［5］张博浩，郭彦林，赵思远，等.张弦梁张拉过程平面外稳定性分析及施工方案比较［J］.施工技术，2012，7（2）：49-54.

Zhang Bohao，Guo Yanlin，Zhao Siyuan，et al.Out-of-plane buckling analysis of beam string structure during tensioning construction and construction schemes comparison［J］.Construction Technology，2012，7（2）：49-54.（in Chinese）

［6］杨勇，李伟政，盛和太.青岛国际帆船中心媒体中心钢屋面结构稳定分析与设计［J］.钢结构，2006，21（5）：11-13.

Yang Yong，Li Weizheng，Sheng Hetai.Stability analysis and design of steel roofing of qingdao international sailboat center［J］.Steel Construction，2006，21（5）：11-13.（in Chinese）

［7］ Midas研发人员.Midas Gen帮助文件［M］.MIDAS IT，2019.

Researchers and Developers.Midas Gen help file［M］.MIDAS IT，2019.（in Chinese）

［8］王玉镯，傅传国.ABAQUS结构工程分析及实例详解［M］.北京：中国建筑工业出版社，2010.

Wang Yuzhuo，Fu Chuanguo.Structural engineering analysis and case study［M］.Beijing：China Architecture & Building Press，2010.（in Chinese）

［9］ GB 50010—2010 混凝土结构设计规范［S］.北京：中国建筑工业出版社，2010.

GB 50010—2010 Code for design of concrete structures［S］.Beijing：China Architecture & Building Press，2010.（in Chinese）

The String-Beam Design of a Gym Roof

JINHan*

（Beijing Institute of Architectural Design， Beijing 100045， China）

The layout of a certain stadium is 69.2 m×21.0 m.In order to meet architectural effect， a truss with 15 one-way string beams was arranged in the 21.0 m span direction.Two softwares were adopted， Midas Gen for overall analysis and Abaqus for node analysis. Safety of the string beams was ensured from four aspects： ① Determination of initial tension according to equilibrium state； ② Solution of large horizontal force generated by flat upper chord of the string beams by adjusting construction sequence. ③ Calculation of stability of the upper chord by linear and nonlinear buckling analysis. ④ Calculation of complex joints by nonlinear analysis of materials. The above four aspects ensure safety and reliability of the project， and can provide reference for the design of similar beam structures.

initial tension， construction stage simulation， buckling analysis， joint analysis

2021-03-01

联系作者：中文作者简介:金 汉，硕士，工程师，一级注册结构工程师，从事结构工程设计与研究。E-mail：547059547@qq.com。