钢桁架内支撑体系柔性交叉支撑门槛刚度设计分析
李永华 揭一鸣 孙果果 章伟豪
钢桁架内支撑体系柔性交叉支撑门槛刚度设计分析
李永华*揭一鸣 孙果果 章伟豪
(南昌大学建筑工程学院,南昌 330031)
近年来,一种钢桁架内支撑体系在深基坑支护中逐步得到推广。本文分别对剪切变形情况下,横系杆完全刚性时柔性交叉支撑的门槛刚度及交叉支撑完全刚性时横系杆的门槛刚度解析解进行了推导,得出了两种情况下的横系杆、交叉支撑的门槛刚度。通过有限元算例进行对比分析,发现随着节间数增大,只考虑剪切变形的交叉支撑门槛刚度误差越来越大,无法满足工程应用需要。对钢桁架内支撑进行考虑弯剪变形共同作用下的整体稳定分析,提出了当横系杆完全刚性时、可同时考虑弯剪变形的交叉支撑门槛刚度实用修正公式,该修正公式具有较高的精度,可满足工程设计实践需求。
钢桁架, 稳定, 门槛刚度, 弯曲变形, 剪切变形
0 引 言
近年来,一种采用张弦梁与型钢桁架相结合的装配式基坑内支撑体系逐渐兴起,该支撑体系采用钢桁架内支撑代替传统的混凝土内支撑进行支护,两榀钢桁架内支撑之间采用大跨度张弦梁结构,增加了桁架内支撑之间的距离,增大了基坑的施工操作空间,加快了施工进度,减少了混凝土的消耗,是一种绿色环保支护形式。对于临近地铁或铁路[1-3]的深基坑,钢桁架内支撑还可以在内支撑端部施加预应力来控制地铁隧道或铁路路基的变形,具有十分重大的工程意义。图1为钢桁架内支撑现场施工图,钢桁架弦杆(分肢)采用高强螺栓进行刚性连接,横系杆、柔性交叉支撑与弦杆之间采用铰接连接,施工安装和后期拆卸都很方便[4]。从图1可以看出,钢桁架内支撑横系杆通常与弦杆采用相同的截面,其刚度一般远大于横系杆支撑门槛刚度,柔性交叉支撑的刚度设计是关键。

图1 钢桁架内支撑现场施工图
钢桁架内支撑为两端铰接轴向受力体系,根据其轴向受压屈曲变形特性,可以取半结构模型进行分析,即采用一端铰接固定、另一端悬臂的计算模型,如图2所示。从图2可以看出,半结构模型类似于采用交叉支撑的柱列模型[5-9],当内支撑节间数为偶数时,半结构节间数正好取一半;当节间数为奇数时,由于中间节间交叉支撑应力为零,半结构模型的节间数可取(-1)/2。
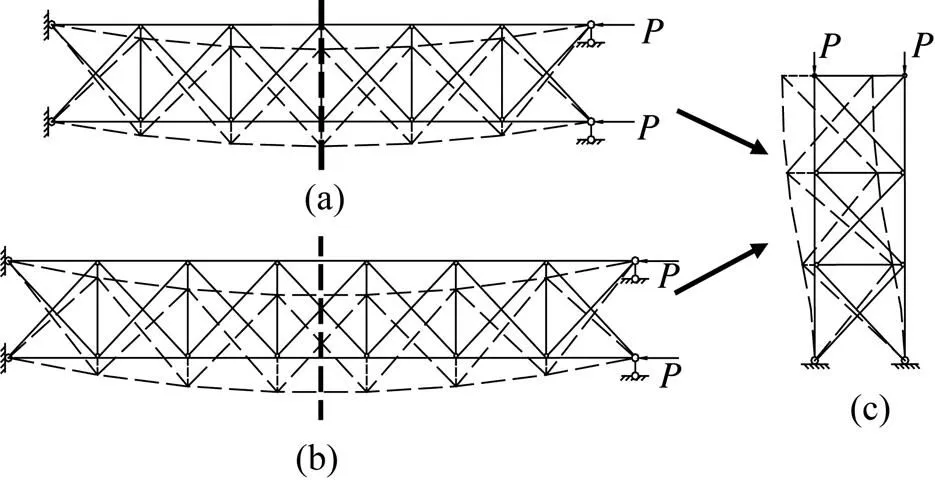
图2 半结构等效计算模型图
文献[5]对横系杆完全刚性时双层两柱体系的交叉支撑门槛刚度进行了分析,还同时分析了交叉支撑跨完全刚性时(将交叉支撑跨视作固定的铰支端)多根柱组成的柱列横系杆门槛刚度。
文献[5]得出的横系杆完全刚性时交叉支撑的门槛刚度公式,是以双层两柱模型为基础,该公式对更多层模型是否成立还需要进一步研究;当交叉支撑采用柔性支撑时(图1),柔性支撑通常只考虑拉杆受力,柔性支撑完全刚性时横系杆的门槛刚度还需要进一步研究。
另外,文献[5]在推导过程中没有考虑柱子的竖向变形,只考虑了柱列支撑体系的剪切变形,但工程实践中钢桁架内支撑已有长度超过130 m的工程实例,不考虑支撑体系的弯曲变形引起的弦杆轴向变形可能会造成一定的误差[10],也需要进一步研究。
1 只考虑剪切变形时三层双柱体系横系杆、交叉支撑的刚度要求


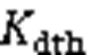
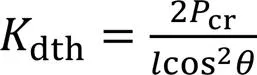

现对三层两柱模型横系杆完全刚性时柔性交叉支撑门槛刚度、柔性交叉支撑完全刚性时横系杆的门槛刚度进行分析,由于稳定分析时交叉支撑只能斜拉杆受力,斜压杆不受力,故分析模型中只考虑一侧斜拉杆作用。
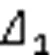
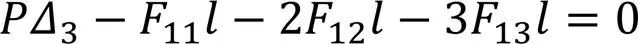
左柱隔离体如图4所示,记柱AB段、BC段、CD段侧移分别为1、2、3,列分段平衡微分方程:
当0<≤时,
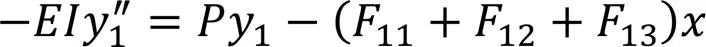
当<≤2时,
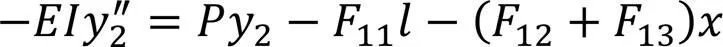
当2<≤3时,


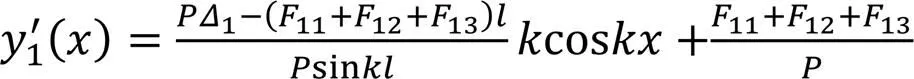
利用边界条件2()=1、2(2)=2,得到:


利用边界条件3(2)=2、3(3)=3,得到:


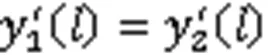
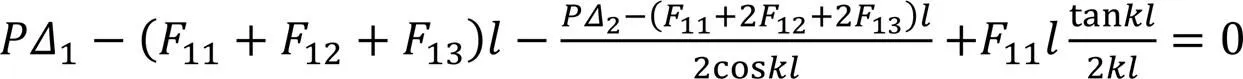
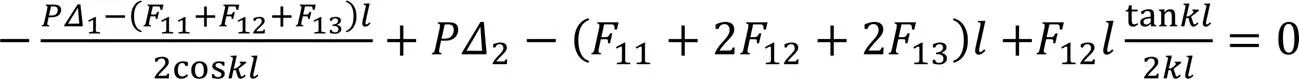
将式(8a)与式(8b)分别相加和相减,可以得到:
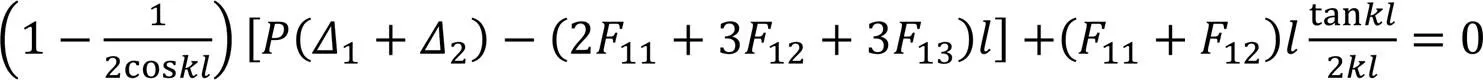
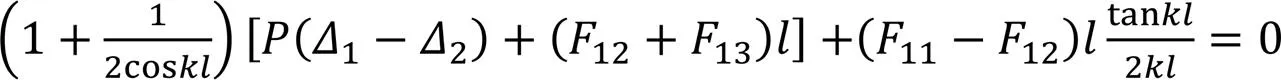
将式(3)分别代入式9(a)、式9(b),则有:
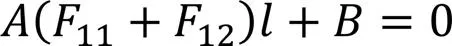

式中:

由式(10a)、式(10b)可以解出:


将式(11a)、式(11b)代入式(3)可以得出:
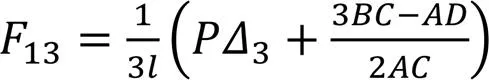
1.1 柔性交叉支撑完全刚性时横系杆门槛刚度


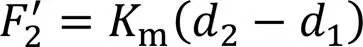

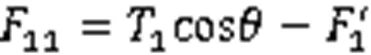




图5 柔性交叉支撑完全刚性时三层双柱分析模型



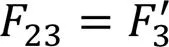
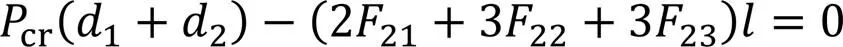
将式(14a)—式(14c)代入式(15)可得:

将1=0、2=1,3=2代入式(11a)—式(11c)求出:
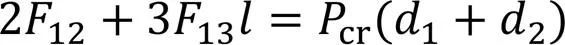
将式(12a)、式(12b)及式(17)代入式(16)可得:

要使得式(18)恒等于零,则
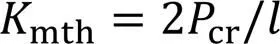
1.2 横系杆完全刚性时柔性交叉支撑门槛刚度
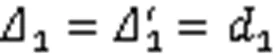

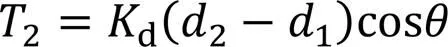
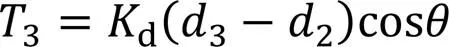

图6 横系杆完全刚性时三层双柱分析模型
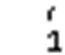
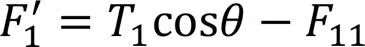


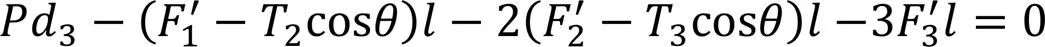


将式(20a)—式(20c)和式(21a)—式(21c)代入式(22a)得:
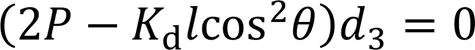
要使得式(23)恒等于零,则

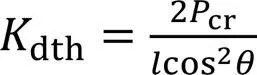
将式(22b)和式(22c)相加:

将式(20a)—式(20c)和式(21a)—式(21c)代入式(26)得:
大豆对土壤要求很高,土壤太松不利于大豆的稳定性,在风雨的情况下容易塌陷;土壤太密不利于大多数根系的生长,大豆不容易吸收养分,造成大豆作物的养分缺乏。不能获得高产量。因此,有必要定期更新土壤,中和深浅层土壤,使土壤适合浅层土壤,疏松适合大豆种植。同时,我们也要考虑季节的变化,冬季土地容易冻结,在早春,不容易播种,所以在冬季到来之前要进行土壤更新,控制土壤厚度,为早春播种创造良好的基础。
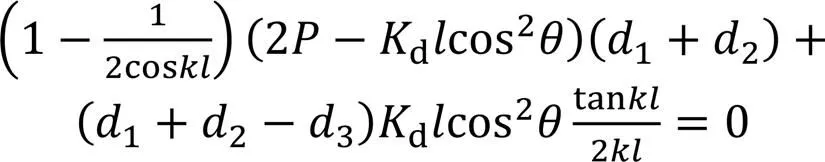
再将式(24)代入式(27)可得:

将式(20a)—式(20c)、式(21a)—式(21c)代入式(22b),并结合式(24)及式(28)可得:
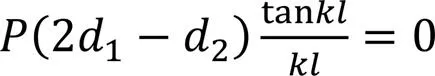

2 有限元分析验证
为验证横系杆完全刚性时柔性交叉支撑的门槛刚度,建立含个节间钢桁架模型(=3~15),内支撑两端铰支,如图7所示,内支撑节间长度=6 m,两分肢之间的距离=7.5 m,钢桁架分肢、横系杆均采用H型钢600×300×20×30,此时横系杆的刚度为7.91×105kN/m。

图7 n个节间的钢桁架柔性交叉支撑模型
采用ANSYS软件对钢桁架内支撑体系进行弹性特征值屈曲分析,采用不同面积的交叉支撑进行反复试算,当桁架体系刚好发生个半波屈曲模态时,此时交叉支撑刚度为有限元验证门槛刚度,并与式(25)计算的交叉支撑门槛刚度dth进行对比,表1为两种方式下交叉支撑门槛刚度的计算结果。
由表1可知,随支撑节间数的增大,式(25)计算得出的交叉支撑门槛刚度dth与有限元计算得出的门槛刚度误差逐渐增大,这主要是因为式(25)在推导过程中只考虑了内支撑桁架体系的剪切变形,没有考虑桁架体系弯曲变形,桁架越长,弯曲变形越明显,式(25)得出的门槛刚度误差就越大。
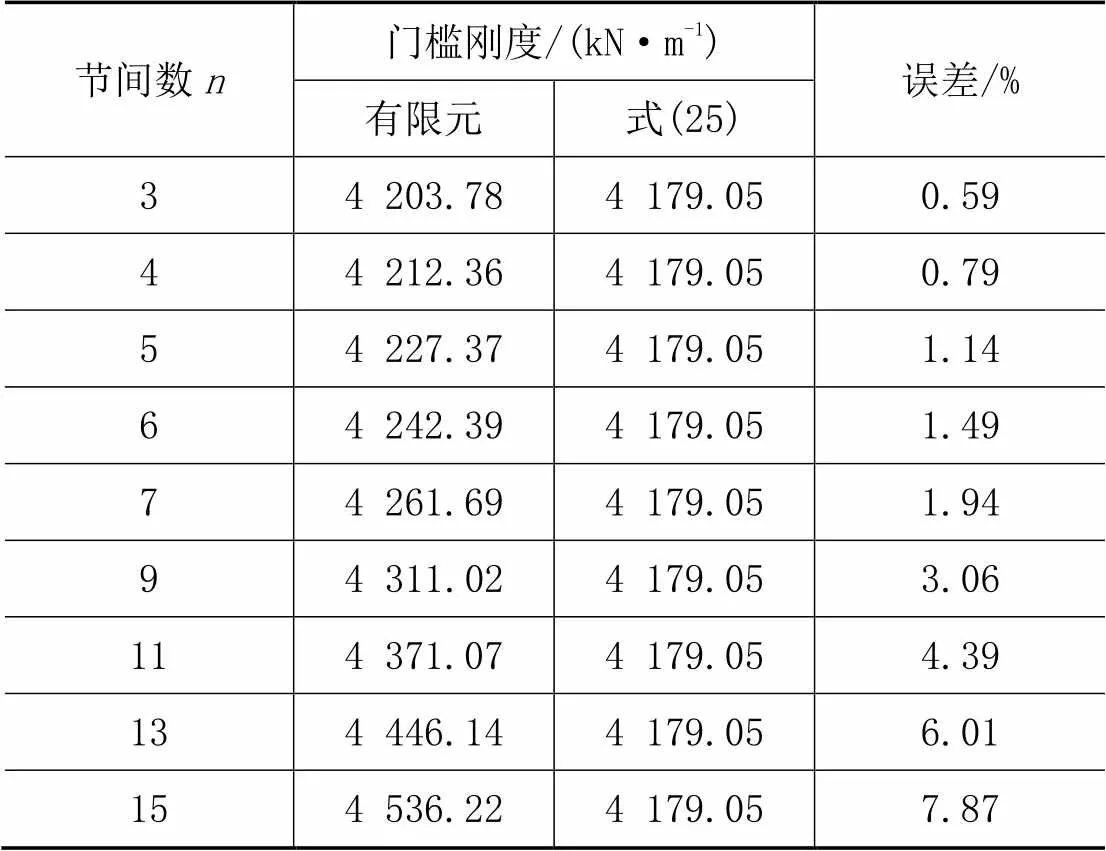
表1 式(25)计算门槛刚度与有限元验证刚度对比
3 考虑弯剪变形的门槛刚度


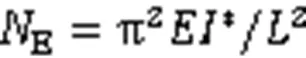

式中:1为斜拉杆长度;为节间长度。
将式(31)代入式(30),可得:

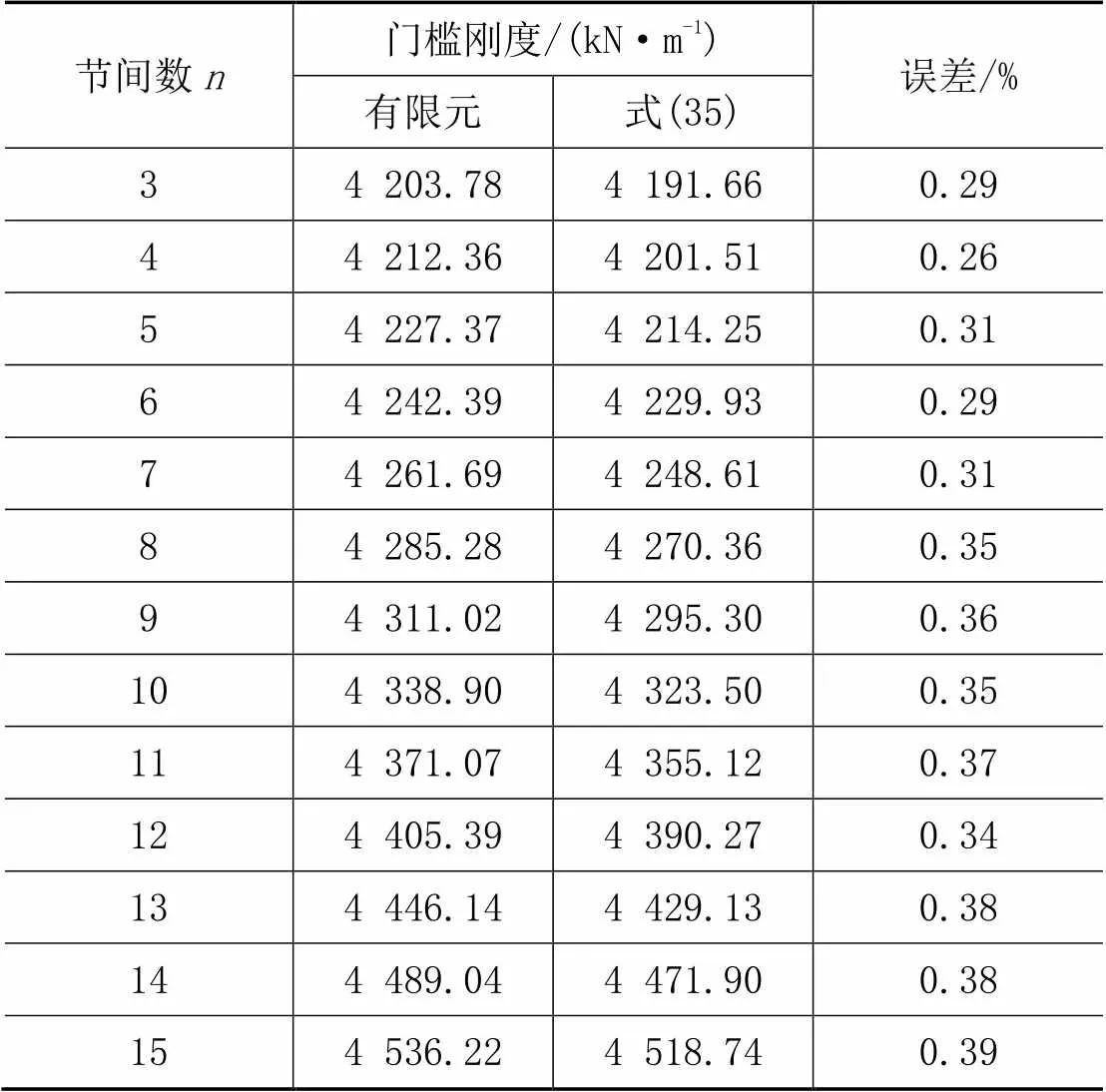
当0 式中:为只考虑剪切变形影响的钢桁架单肢稳定承载力;0为同时考虑弯曲和剪切变形影响时的钢桁架整体稳定承载力,式(33)右边值恒大于1,说明在斜拉杆刚度小于或等于门槛刚度dth时,同时考虑弯剪变形的桁架稳定承载力恒小于只考虑剪切变形时的桁架稳定承载力。 从式(35)还可以看出,由于钢桁架支撑单肢惯性矩一般远小于整体惯性矩*,故当较小时,对交叉支撑门槛刚度修正影响较小,但当比较大时,2影响就比较明显,不可以忽略。 现采用式(35)来继续计算上个算例的交叉斜撑的门槛刚度,具体计算结果见表2,由表2可知,ANSYS有限元计算结果与式(35)的结果非常吻合,其原因在于式(25)是只考虑了结构的剪切变形,而式(35)同时考虑了结构的弯曲和剪切变形,所以门槛刚度会随着节间数的增大而发生变化。 表2 式(35)计算门槛刚度与有限元验证刚度对比 通过研究,可以得到以下主要结论: (1) 随着钢桁架内支撑长度的增加,只考虑剪切变形影响得出的横系杆完全刚性时柔性交叉支撑的门槛刚度误差会越来越大,无法满足工程实践需求。 (2) 在此基础上提出可同时考虑弯剪变形影响的柔性交叉支撑门槛刚度实用修正公式,该修正公式具有较高的精度,可满足工程设计实践需求。 [1]宗翔.基坑开挖卸载引起下卧隧道隆起的控制方法[J].结构工程师,2020,36(3):198-205. Zong Xiang.Control method of tunnel heave caused by excavation and unloading of foundation pit[J].Structural Engineers,2020,36(3):198-205.(in Chinese) [2]李宁,张祥,张得煊,等.考虑槽壁及坑底联合加固的上海地铁车站基坑变形特性分析[J].结构工程师,2020,36(1):148-154. Li Ning,Zhang Xiang,Zhang Dexuan,et al.Analysis of deformation characteristics of foundation pit of Shanghai Metro Station considering joint reinforcement of trench wall and pit bottom[J].Structural Engineers,2020,36(1):148-154.(in Chinese) [3]刘克文,阮永芬,林君伟,等.深基坑联合支护对临近地铁的影响分析[J].结构工程师,2017,33(4):193-199. Liu Kewen,Ruan Yongfen,Lin Junwei,et al.Effect of combined support of deep foundation pit on adjacent structures influence analysis of iron[J].Structural Engineers,2017,33(4):193-199.(in Chinese) [4]相阳,罗永峰,黄青隆.装配式钢结构抗震性能研究进展[J].建筑钢结构进展,2019,21(3):1-12. Xiang Yang,Luo Yongfeng,Huang Qinglong.Research progress on the seismic performance of prefabricated steel structures[J].Progress in Steel Building Structures,2019,21(3):1-12.(in Chinese) [5]童根树,饶芝英.双层纵向柱列支撑的设计要求[J].建筑钢结构进展,2007,9(3):50-57. Tong Genshu,Rao Zhiying.Design requirements of bracings in two-story longitudinal frames[J].Progress in Steel Building Structures,2007,9(3):50-57.(in Chinese) [6]赵金友,张耀春.竖向荷载下纵向柱列交叉支撑刚度要求[J].工业建筑,2011,41(2):78-82. Zhao Jinyou,Zhang Yaochun.Design stiffness requirements of diagonal bracings for longitudinal column-bracing system under vertical loads[J].Industrial Construction,2011,41(2):78-82.(in Chinese) [7]赵金友.竖向荷载下纵向柱列支撑的设计方法研究[D].哈尔滨:哈尔滨工业大学,2009. Zhao Jinyou.Bracing design method of longitudinal column-bracing system under vertical loading[D].Harbin:Harbin Institute of Technology,2009.(in Chinese) [8]李东.纵向支撑框架稳定性分析及支撑设计要求[D].杭州:浙江大学,2005. Li Dong.Stability analysis and bracing requirements of longitudinal braced frames[D].Hangzhou:Zhejiang University,2005.(in Chinese) [9] Muhammad Qasim,Jamal Ali,Shaukat Ali Khan.Structural response of RC frame under seismic loading by varying inclination angle of cross bracing[J].International Journal of Structural Engineering,2016,7(2):169-179. [10]方鄂华.多层及高层建筑结构设计[M].北京:地震出版社,1992. Fang Ehua.Structural design of multi-storey and high-rise buildings[M].Beijing:Seismological Press,1992.(in Chinese) [11]陈绍蕃.具有多道弹性支撑杆的钢柱稳定计算[J].西安建筑科技大学学报(自然科学版),2011,43(2):153-159,276. Chen Shaofan.Stability calculation of steel columns with multiple elastic braces[J].Journal of Xi'an University of Architecture and Technology(Natural Science Edition),2011,43(2):153-159,276.(in Chinese) [12]陈绍蕃.钢结构稳定设计指南[M].3版.北京:中国建筑工业出版社,2004. Chen Shaofan.Guide to stability design of steel structures[M].3rd ed.Beijing:China Architecture and Building Press,2004.(in Chinese) [13]陈绍蕃.钢结构设计原理[M].3版.北京:科学出版社,2005. Chen Shaofan.Principles of steel structure design[M]. 3rdEdition.Beijing:Science Press,2005.(in Chinese) [14]杨天祥.结构力学[M].北京:高等教育出版社,1987. Yang Tianxiang.Structural mechanics[M].Beijing:Higher Education Press,1987.(in Chinese) [15]梁启智,林道勤,王仕统.钢结构[M].广州:华南理工大学出版社,1988. Liang Qizhi,Lin Daoqin,Wang Shitong.Steel structure [M].Guangzhou:South China University of Technology Press,1988.(in Chinese) Design and Analysis of the Cross Flexible Bracing Critical Stiffness for Steel Truss Internal Support System LIYonghua*JIEYiming SUNGuoguo ZHANGWeihao (Architectural and Civil Engineering Institute,Nanchang University, Nanchang 330031, China) In recent years, a kind of steel truss internal support system has been gradually popularized in excavation support. The critical stiffness requirements of the flexible bracing and lateral bracing are derived when the other was rigid under shear deformation, and the critical stiffness of the cross bracing and the lateral bars are derived. Through the comparative analysis of the finite element examples, it is found that with the increase of the number of joints, the critical stiffness error of the cross bracing becomes larger and larger only considering the shear deformation,which can not meet the needs of engineering application. The overall stability analysis of steel truss internal support under the combined action of bending and shear deformation is made. A practical correction formula for the cross bracing critical stiffness is proposed considering both bending and shearing deformation. The modified formula has high accuracy and can meet the engineering design requirements. steel truss, stability, critical stiffness, bending deformation, shear deformation 2021-03-16 国家自然科学基金项目(51168037) 联系作者:中文作者简介:李永华(1972-),男,江西人,副教授,博士,主要从事结构抗震和防灾减灾研究。E-mail: leeyhncu@163.com




4 结 论

