基于粒子群优化的移动机器人MCL全局定位算法
龚建铭,范 阳,周建辉
(1.北京科技大学顺德研究生院,广东 佛山 528399;2.北京科技大学 机械工程学院,北京 100083;3.华北理工大学迁安学院 机械工程系,河北 迁安 064400)
1 引言
全局定位是指:移动机器人丢失位姿估计时,如何根据传感器信息来重新估计自身位姿的问题[1],是机器人能够承担地图构建、导航、目标检测及跟踪等任务的基础[2]-[4]。针对该问题的研究由来已久,其中基于贝叶斯滤波(Bayes filter)的定位方法可以提供很好的全局定位解决方案[5]。在贝叶斯滤波框架下,扩展卡尔曼滤波(Extended Kalman Filter)定位算法[6]-[7]可以精确实现机器人定位,但由于高斯分布的单峰特性,该类算法无法有效解决全局定位问题。多假设跟踪定位算法[8]将保留多个位姿的假设并使这些假设进行状态的更新,以此来实现全局定位。蒙特卡洛定位(MCL)算法[9]-[10]作为一种基于粒子滤波的实现方式,采用带有权重值的粒子集来近似表示任意的后验概率分布。然而,由于该算法进行全局定位时采用了次优先级的重要性函数,存在有粒子贫乏和计算效率较低的问题。[11]
为了避免MCL算法需要大量粒子来确定初始状态而导致计算效率低的问题,Zhang等人[12]基于雷达放置在AGV正中心的假设,提出了相似能量区域SER(Similar Energy Region)的SAMCL算法采样方法,即预先判断每个粒子周围的环境状态来提高全局定位的效率。Dihua等人[13]提出了种自适应的KLD(Kullback-Leibler Divergence)采样方法,该方法通过K维树来调整箱样本集的大小和样本分布的变化。Zhang等人[14]将全局定位问题划分为初始位姿估计与位姿两个阶段,提出将粒子群优化算法与粒子滤波器方法相结合,来提高定位算法的性能。章洋等人[15]增加了线段特征匹配的过程用于缩小定位范围,从而改善定位的精度和实时性。
本文针对移动机器人全局定位时机器人可能发生的碰撞、打滑和被人为搬运等情况而导致的位姿估计失效问题,当认为位姿估计偏差较大时通过引入粒子群优化算法来对粒子集的分布进行优化,并将这一方法与MCL算法相结合,使得定位算法在该种情况下能够准确地恢复位姿估计。
2 基于粒子群优化的移动机器人MCL全局定位算法
本文计划在机器人位姿丢失的情况下引入PSO来恢复位姿估计。PSO和原有MCL算法框架下的重要性采样都具有随机性,同时优化机器人位置与姿态将导致定位算法的结果不稳定。所以,PSO只应用于重新估计位置,对于姿态的估计仍然依靠重要性采样来实现当前预测粒子集Sˉt对粒子集St的近似。
2.1 粒子群优化算法
PSO是Kennedy和Eberhart等人[10]于1995年提出的一种受鸟群觅食行为而启发的智能优化算法,与MCL算法一样,每一个粒子都代表实际问题的可行解,二者存在相融合的应用价值。
所有粒子按公式(1)、(2)更新其速度与位置,以寻找状态空间中的最优适应度值:

其中,w(t)为惯性权值;r1,r2为服从0~1之间均匀分布随机数;c1,c2为学习因子,一般取c1=c2=2。
2.2 基于粒子群优化的移动机器人MCL全局定位算法(PSO-GL)
为了将粒子的平移分量和旋转分量相分离以便恢复对机器人位置的估计。从条件输入入手:将栅格地图模型M与当前观测A转换为与方向无关的描述。
(1)观测数据转换为与方向无关的描述
假设使用能够360度扫描的激光雷达进行定位与建图。则对于雷达的观测数据来说,可根据ρi的大小将ρi进行分类。记需要划分的间隔大小为gap,雷达的最大观测距离为max_range。条件输入为观测数据输出为表征与旋转无关的描述向量vA。具体步骤如下:
步骤1定义一个零向量vA,其大小为max_range/gap+1;
步骤2对于每一个ρi∈A,计算的值并将中的值计数+1,对于激光雷达可能存在返回NaN(Not a Number)的情况,向量vA存储存在NaN情况的个数;
步骤3对向量vA进行归一化处理。
(2)预缓存的地图位置描述
受文献的启发,使用预缓存的地图表达技术将地图M表达为相应栅格分辨率的二维栅格地图G2D。在G2D的每一个栅格处可采用Ray casting算法产生模拟的观测数据并进行对观测数据的转换。最后将所有转换的数据存储在G2D相对应的栅格中。对于使用该策略的改进算法而言,以后的每次迭代中只需要查找G2D中对应栅格点的描述值就能得到该点处的与方向无关描述向量v。其实,不论模拟观测的姿态角设置为多大,由于对观测数据的转换只记录落在相应间隔点的个数,其对G2D不造成影响,所以只需将姿态角设置为0。最后得到的结果是G2D的各个元素对应其地图M的与旋转无关描述的表达。
得到观测数据和地图模型的与旋转无关描述就可以利用PSO搜索初始位置。具体地,在初始位姿估计时对于当前观测A与具有位置的某一粒子Xi来说,其相应的适应度值定义为它们观测的与方向无关描述vA,vX,之间的余弦距离:

确定了在位置搜索下的适应度值就能将基于该改进策略的PSO进行粒子集位置的重新计算。机器人在运行中获得运动数据ut、观测数据vt的同时,PSO-GL算法会不断进行在MCL算法框架下进行位姿递推,直到PSO-GL算法认为发生位姿估计失效的情况,即对于有效粒子数
步骤1由当前的预测粒子集Sˉt为输入,在G2D中查找对应的与方向无关的描述向量v;对于当前观测数据A进行同样的转化得到vA。
步骤2由公式(3)计算各个粒子的适应度值,并进行个体极值pbest、全局极值gbest的初始化;
步骤3由公式(1)、(2)更新每个粒子的速度、位置,若存在更新后粒子超出地图边界的情况,则将其随机分布于地图中;
步骤4重新计算粒子集的适应度值,将个体极值和全局极值进行比较,寻找最大的极值并将其替换gbest;
步骤5判断是否达到终止条件,若达到终止条件,则移动至步骤6;若未达到终止条件,则回到步骤3;
步骤6 PSO算法输出更加符合当前预测的粒子集-S′t,将-S′t进行测量更新与重要性采样得到粒子集Sˉt。
PSO-GL算法的总体流程图如图1所示。
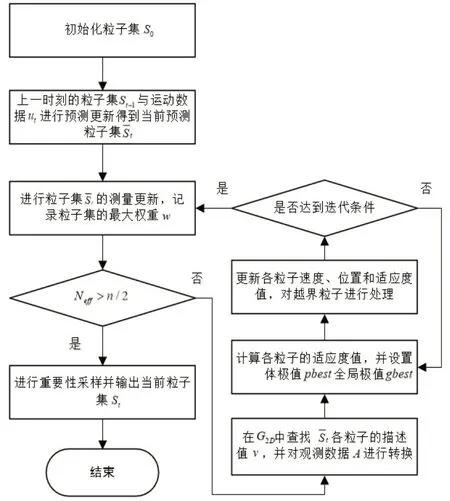
图1 PSO-GL算法
3 全局定位算法算法仿真实验
3.1 仿真地图环境
在Matlab下搭建与文献[16]相类似的仿真地图环境MRL Arena,如图2(a)所示,其中地图大小为5.55m*5.02m,分辨率为0.01。
设定激光雷达最大量程max_range、角度噪声和径向噪声σθ,σr,则可通过光线投影算法模拟在此位姿下机器人所获得的环境观测信息,如图2(b)所示。
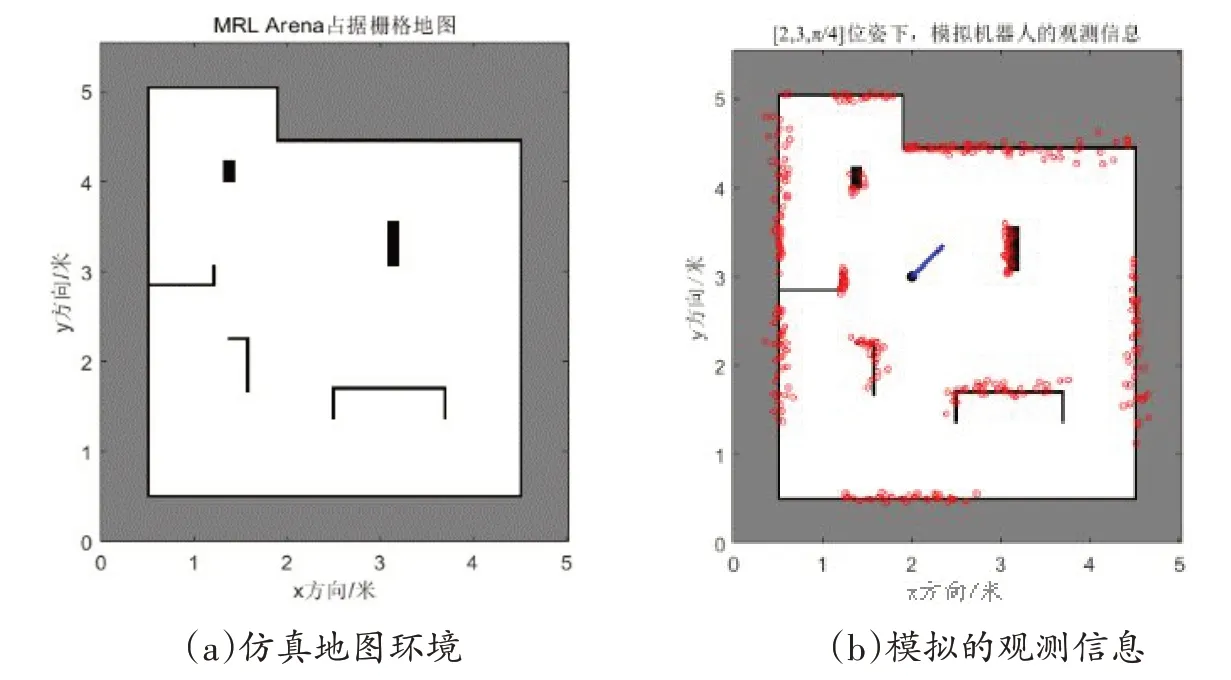
图2 MRL Arena仿真环境下的地图和观测信息
3.2 仿真实验
在t=4时,添加扰动量F=(0.2,0.4,0.3)。实验参数的设置为:PSO-GL算法与MCL算法的粒子集规模nPSO-GL=nMCL=300;PSO-GL算法位姿失效恢复部分中,迭代次数k=5,学习因子c1=c2=2,定义收缩因子

参数c=c1+c2,粒子按照按公式(1)、(2)、(6)进行更新:

在运动过程中,机器人运动的真实轨迹、PSO-GL的估计轨迹以及MCL算法估计的轨迹如图3所示。
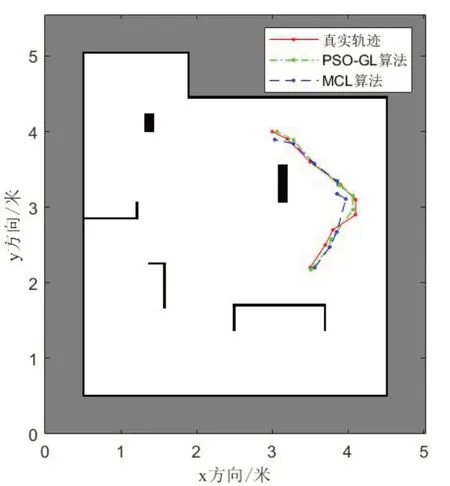
图3 仿真实验中真实轨迹和PSO-GL算法、MCL算法估计的轨迹
t=4时,由于添加了添加扰动量F,MCL算法中运动更新后的粒子集分布于真实位姿存在较大偏差,故此时MCL算法估计这类问题的能力只能取决于少数随机分布,并且被认为是在上一时刻估计“不准确”的粒子,并由这些粒子根据重要性采样阶段来产生更多的粒子,以此来估计机器人的位姿。PSO-GL算法和相比这一方式,额外存在有基于PSO的位置调整策略,使得所改进算法对这类位姿估计失效问题不敏感。提取两种算法各自估计的机器人位姿点,分析其各自的估计误差,如图4所示。

图4 仿真实验中PSO-GL算法、MCL算法的估计误差
MCL算法的位置估计误差与角度估计误差分别增大了412.5%,700.1%;而PSO-GL算法的位置估计误差略微减小41.9%。角度估计度误差增大了361.2%。可见,PSO-GL算法对扰动量F鲁棒,其具体结果是:在发生扰动后,PSO-GL算法的位姿估计恢复部分使得PSO-GL算法的位置估计精度得到了提高,相应地,扰动量F对PSO-GL算法的角度估计误差影响也明显小于MCL算法。
4 移动机器人地图构建与全局定位实验
4.1 地图构建实验
本文所进行的物理实验是基于HuanYuBot移动机器人实现的,其总体结构如图5所示。

图5 HuanYubot机器人的总体结构
HuanYuBot机器人采用思岚A1雷达作为外部传感器并以机器人操作系统(ROS)为平台来实现实验场景地图的构建。本文的实验地点为某研究生实验室,该场景主要由实验室工位以及过道组成,如图6所示。

图6 进行建图实验的场景
采用Gmapping开源算法来构建实验室的地图。在地图构建的过程中,为了使得地图避免出现地图障碍物点或出现类似于“褶皱”的情况,应该尽量将机器人的直行和旋转运动分开。最终,通过rosrun命令启动map_saver节点保存地图文件,得到地图map.pgm与地图的描述文件map.yaml。构建的实验室栅格地图如图7所示。其中,蓝色的小车部分为机器人模型,红色的点云部分为当前位姿下的激光雷达数据。地图的大小为20.8m×14.55m,地图分辨率为0.05。
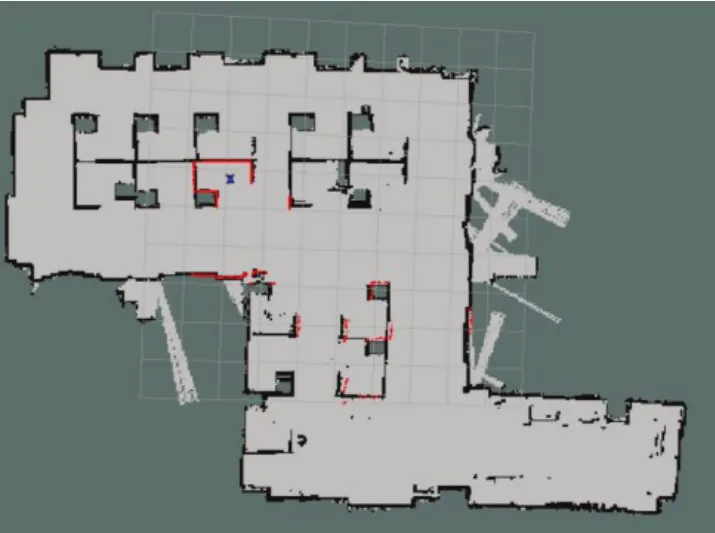
图7 构建的栅格地图
4.2 全局定位实验
控制机器人移动到实验室的任意位姿,记录在这些位姿下激光雷达观测数据以及位姿之间的里程计变化量,通过rosbag record命令保存得到bag文件,并将地图文件与这些数据导入到Matlab中,PSO-GL算法和MCL算法的估计精度。实验参数的设置与3.2一致。
如图8所示,a点到j点为机器人运动的真实轨迹,为了验证所提出算法对机器人位姿估计失效恢复的性能,e点到f点之间存在较大的位移且只记录这一段间隔的部分里程计数据。
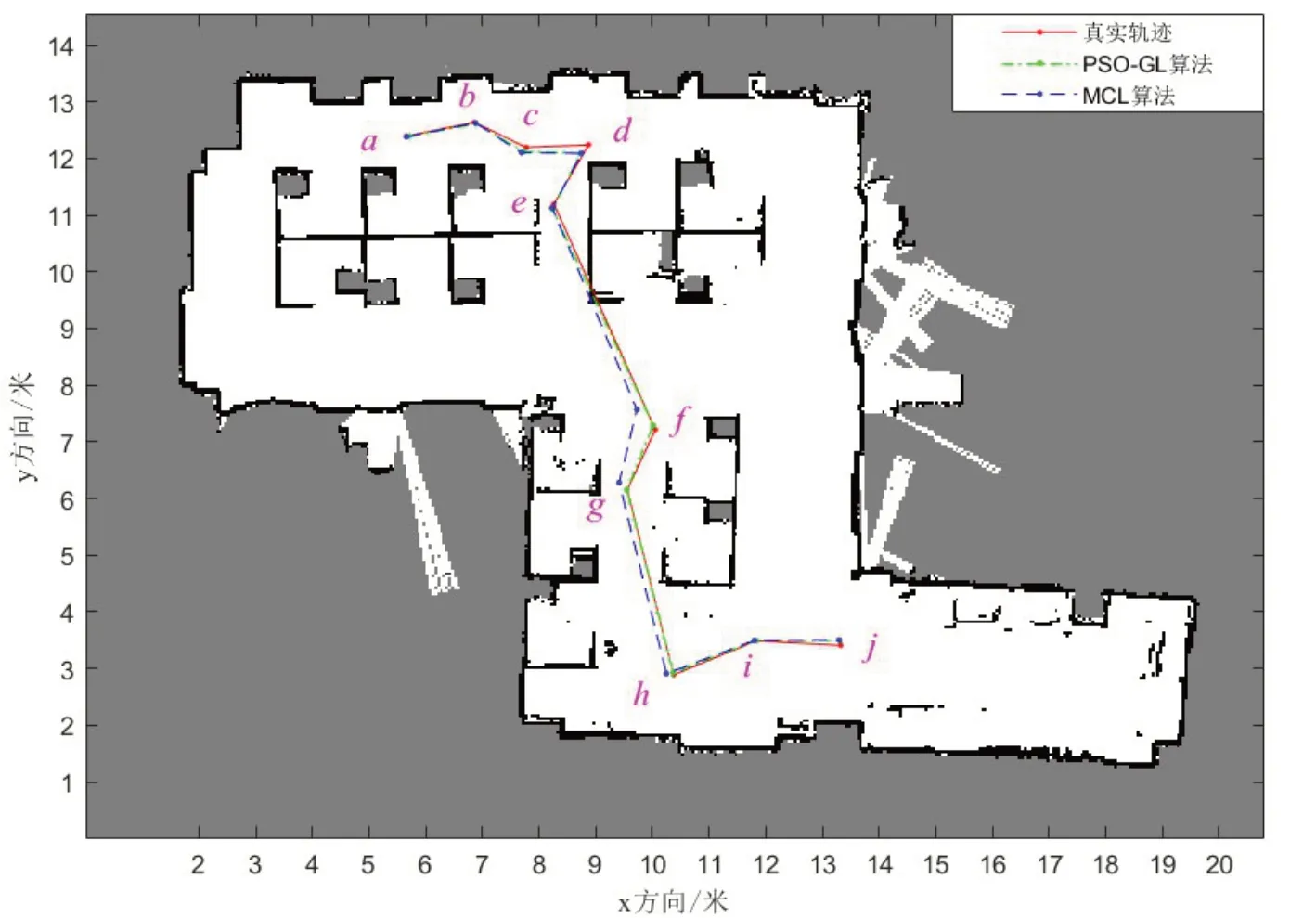
图8 真实轨迹和PSO-GL算法、MCL算法估计的轨迹
可见,除了f点之外三条不同颜色的轨迹线大体上是相接近的,两种算法大致都能较好地跟踪机器人的位置,由于e点到f点之间只记录了部分的运动数据使得MCL算法估计的位置产生了较大偏差,而基于PSO的位置估计改进策略使得PSO-GL算法能够将粒子集朝更加符合观测信息的高似然区域移动,从而在f点具有更好的位置估计精度。提取两种算法各自估计的机器人位姿点,分析其各自的估计误差,如图9所示。
t≠6时,PSO-GL算法的位置估计误差均值、角度估计误差均值分别为0.0563m、-0.0275rad,而MCL算法的位置估计误差均值、角度估计误差均值分别为0.0688m、-0.0328rad,可见两种算法在没有位姿估计失效的情况下估计精度相差不大。
t=6时,由图9可见,MCL算法的位置估计误差与角度估计误差分别增大了267%,375%;而PSO-GL算法的位置估计误差略微减小40%。角度估计度误差增大了220%。故PSO-GL算法能够对粒子集的预测分布与真实分布之间存在较大偏差的情况进行响应,粒子集能够朝向真实分布的区域移动,其最终结果使得PSOGL算法对粒子集的预测阶段产生的偏差鲁棒,有效减少位置估计误差并使得角度估计偏差也随之减小。
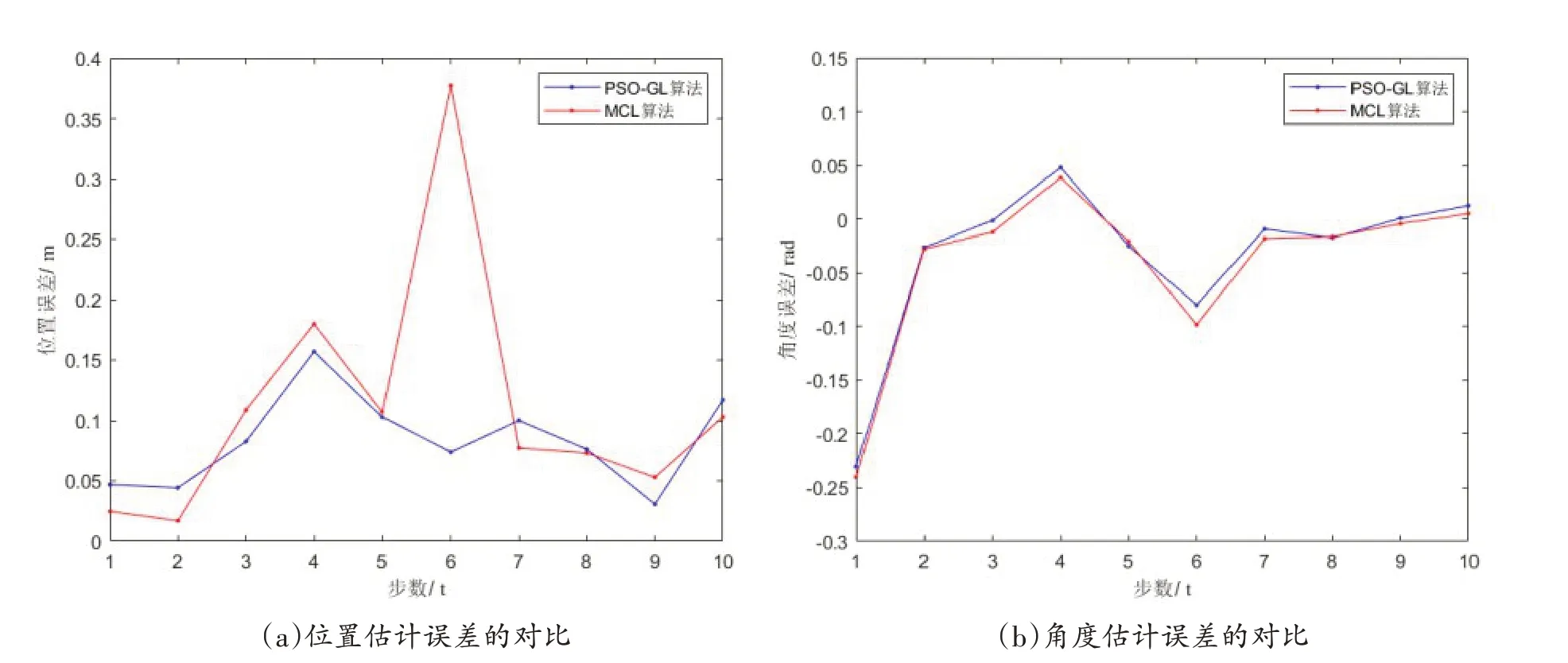
图9 PSO-GL算法和MCL算法的估计误差对比
5 结论
本文将PSO引入到MCL算法中来,通过判断当前预测粒子集Sˉt中的有效粒子数目来识别定位算法是否存在位姿估计丢失的情况,通过PSO对粒子的采样进行优化,使得采样分布向观测概率较高的位置移动并依靠重要性采样完成粒子集位置的更新。在仿真和物理实验下的结果表明,PSO-GL算法对位姿估计失效的情况鲁棒、位置估计误差较MCL算法显著减少,角度估计误差的增幅也小于MCL算法。

