内置轴向屈服板的双层方钢耗能支撑滞回性能分析

徐伟栋，赵宝成

（苏州科技大学 江苏省结构工程重点实验室，江苏 苏州 215011）

中心支撑框架结构抗侧刚度大，是应用比较广泛的一种结构的结构体系。但中心支撑受压易屈曲，导致结构抗侧刚度显著降低。为了提高支撑的耗能能力和变形能力，有学者提出防屈曲支撑[1-2]，防止支撑进入塑性，利用内芯进入塑性耗能，在地震作用下，先于防屈曲支撑主体进入屈服耗能，避免支撑发生失稳。

根据这一设计理念，各国学者提出了众多形式新颖，性能优良的防屈曲耗能支撑构造形式，并针对耗能支撑刚度和承载力计算方法[1]，耗能支撑的布置方式[2]、内芯钢材[3-4]，截面形式[5-7]、滞回性能[8-9]、稳定性能[10-11]等进行了深入研究。严红[12]等对一种一字形全钢防屈曲支撑进行试验研究，结果发现内芯破坏易发生在端部加劲肋处，支撑加载后期内芯承压过程中受压承载力明显高于受拉承载力，未能充分利用钢材的抗拉性能。王玉梅、王爽[13]设计了一种双核芯全钢防屈曲支撑并对其进行试验分析及数值模拟分析，试验过程中，试件端部发生错动，滞回曲线不饱满，出现捏拢现象，结果表明约束单元需保证足够握裹强度，试件端部连接锚固可靠，才能保证核心构件的性能。

单核芯和双核芯防屈曲支撑构件都能实现受压防屈曲，支撑受拉和受压抗压性能不完全一致，同时试验研究表明，防屈曲支撑端部容易出现平面内及平面外失稳[14]。因此，防屈曲耗能支撑的设计必须进行端部加强的设计。为了保证支撑端部不发生局部屈曲，避免支撑在受压时发生失稳破坏，充分利用钢材的抗拉性能，本文提出了一种内置轴向屈服板的双层方钢耗能支撑，构造如图1所示。该耗能支撑主要由内部和外部传力方钢及四块耗能板组成，内部和外部传力方钢对耗能板进行约束，并传递轴向力，耗能支撑通过板铰与框架主体连接。支撑内部耗能板布置于内外方钢之间，与内外方钢连接。两侧边耗能板下部连接外方钢，上部连接内方钢，上下两面耗能板上部连接外方钢，下部连接内方钢。支撑在轴力作用下总存在相互平行的两个面的耗能板在承受拉力同时与之垂直的另两个面的耗能板承受压力，无论在支撑受压或受拉时，总有两块耗能板受拉，从而利用到钢材良好的受拉性能。这种构造的双层方钢耗能支撑端部没有薄弱部位，不会发生端部破坏。

图1 双层方钢耗能支撑构造图

为了研究这种支撑的耗能能力和变形能力，本文采用了ABAQUS有限元软件对支撑进行了仿真模拟，将支撑放置于子结构[15]中，对支撑进行低周往复加载，分析了楔率、耗能板布置方式等参数对双层方钢耗能支撑滞回性能的影响，并给出了支撑的承载力计算方法。

1 支撑设计及参数选取

1.1 支撑设计

本文分析的耗能支撑几何模型如图2所示，BASE支撑总长取为1 951 mm。耗能板总长为L，耗能段宽为H2，耗能板中间段变截面处宽为H1，厚为6 mm。外部方钢长为L1，内部方钢长为L2，截面尺寸分别为□150 mm×6 mm、□120 mm×6 mm，加劲板厚8 mm，端板厚度为20 mm，端板与加劲肋之间的距离50 mm。采用Q235B级钢。

图2 支撑几何尺寸

1.2 设计参数选取

支撑通过内部屈服板进入塑性变形耗散能量，本文研究的影响双层方钢耗能支撑性能的主要设计参数为楔率及耗能板的布置方式。本文设计了三种耗能板布置方式，分别为EDB-1、EDB-2及EDB-3（见图2），其中EDB-2A为BASE试件，根据耗能板的三种方式采用两种楔率，共设计了9个试件，参数见表1。

表1 双层方钢耗能支撑几何参数

2 有限元模型的建立与验证

2.1 钢材的本构关系

钢材本构模型采用等向强化模型，考虑包辛格效应及Mises屈服准则。钢材采用双线性模型。Q235B级钢屈服强度为235 N/mm2，极限强度为474 N/mm2，钢材的弹性模量E为2.06×105MPa，Et为0.02E，泊松比μ为0.3。

2.2 单元划分

所有构件单元均采用八节点线性六面体（C3D8R）一次缩减积分实体单元建模，防止单元之间出现过约束和体积自锁的问题。网格控制属性中，单元形状均采用六面体，对于规则单元采用结构化网格技术，对于不规则单元采用扫掠技术，算法采用中性轴算法，并采用最小化网格过滤。由于耗能板是支撑主要受力变形构件，故进行网格加密，对板件厚度方向均匀划分五层网格。对支撑考虑大变形，打开几何非线性，采用自动稳定（指定衰减因子）。图3为有限元模型网格划分结果示例。

图3 有限元模型网格划分

2.3 接触与边界条件

该支撑中耗能板与内外方钢之间接触采用面与面接触，依据《钢结构设计规范》（GB50017-2017）中在连接处构件接触面的处理方法，采用钢丝刷清除浮锈或未经处理的Q235钢材，摩擦面的抗滑移系数取0.30。其余部件之间均采用绑定接触（tie）连接。接触的法线方向采用“硬接触”，切线方向采用“罚函数”计算摩擦。

支撑两端与加载装置之间采用铰接连接构造形式，如图4所示。于支撑的下端板铰中心和柱的下端板铰中心设置耦合点，用以添加边界条件，支撑和柱绕X轴转动，放松UR1，其余设置为U1=U2=U3=UR2=UR3=0；加载装置施力截面耦合于截面形心点，用以施加位移，施力截面处只发生Y轴向水平位移，于该点施加幅值位移，为使加载装置不发生面外变形，设U1=0。支撑与加载装置连接处通过销轴与板铰连接。

图4 子结构加载装置

2.4 加载制度

有限元模拟中采用位移加载控制方法，对加载装置加载点处施加水平位移。根据《建筑抗震设计规范》中要求的弹塑性层间位移角限制为1/50，则以此作为破坏时的层间位移角。采用位移加载，参考美国Steel-SAC规范[16]，按照0.375%、0.5%、0.75%、1%、1.5%、2%、2.5%加载。加载制度见图5。

图5 加载制度

2.5 有限元模拟验证

选取文献[17]进行有限元模拟验证，支撑为一字型全钢装配式防屈曲支撑的试验，本文采用ABAQUS建立了这根全钢装配式防屈曲支撑的精细化有限元模型，支撑拆解图见图6。有限元模型采用与试验相同的钢材本构关系、边界条件及加载方式。

图6 DA-BRB支撑拆解图

有限元模拟结果与试验对比见图7，发现两者的滞回曲线较为吻合，试验所得的初始刚度以及屈服刚度基本一致，表明2.2节所述有限元方法可用于模拟双层方钢耗能支撑的滞回性能。

3 破坏过程及现象

加载过程中，耗能板端部与方钢连接处未进入塑性，整个耗能板只有耗能段进入塑性耗能。

对EDB-2A试件进行破坏过程的描述，其应力云图如图8所示，左边为支撑上部，右边为支撑下部。加载初期，耗能板从中间段先进入耗能，随后往耗能板两端扩散至整块耗能板进入耗能，耗能板应力分布较均匀，无很明显的应力集中区域。加载中期，随着构件的变形加大，受压区耗能板发生多波屈曲变形，受拉区耗能板受拉平直无屈曲；耗能板上与方钢接触的多波屈曲段处应力较大。加载后期，随着加载位移的增大，耗能板在受压过程中，产生不可逆的的损伤，耗能板发生多波屈曲段先于其他构件发生破坏。

图8 EDB-2A支撑耗能板应力图

通过ABAQUS有限元分析，双层方钢耗能支撑耗能板的破坏模式有两种。一种是耗能板面外发生多波屈曲破坏，一种是耗能板发生面内剪切屈曲破坏。EDB-1系列支撑上部耗能板相对于下部耗能板变形程度大。EDB-2系列支撑由于耗能板较长，耗能板受压发生多波屈曲变形较明显。EDB-3系列支撑耗能板受压区呈多波屈曲变形，受拉区易在耗能板端部受拉破坏。当EDB-1、EDB-2、EDB-3系列支撑楔率增大时，耗能板受压时中间变截面处更易发生屈曲变形，且加载到后期，耗能板变截面处易发生面内侧向屈曲变形，见图9。

图9 支撑耗能板变形图

4 有限元分析结果

通过ABAQUS有限元模拟得到耗能支撑的滞回曲线、骨架曲线、刚度退化曲线，进而分析楔率和耗能板布置方式对双层方钢耗能支撑性能的影响。

4.1 耗能板楔率的影响

4.1.1 EDB-1系列支撑

EDB-1系列支撑总共有八块耗能板,由图10可知EDB-1系列试件的滞回曲线饱满无捏缩，滞回环形状一致。改变楔率，对EDB-1支撑的轴向承载力有较大影响，EDB-1骨架曲线呈二折线型，从骨架曲线可以看出，随着楔率的增加，EDB-1系列支撑的轴向承载力下降明显。主要原因是增加楔率会导致耗能板局部横截面减小；且楔率增加，支撑后期承载力增加缓慢。EDB-1系列试件刚度退化曲线形态相似，总体上呈降低趋势，EDB-1A，EDB-1B，EDB-1C支撑的初始轴向刚度依次为19.96、17.88、15.85 kN/mm。将耗能板楔率改为0.33，初始刚度降低10.4%，耗能板楔率改为0.60，初始刚度降低20.6%。改变楔率会导致EDB-1系列支撑承载力和刚度下降。

图10 EDB-1系列支撑

4.1.2 EDB-2系列支撑

EDB-2系列支撑通过四块耗能板耗能，耗能板较长，支撑受力时，应力分布较均匀。图11可知，EDB-2系列试件的滞回曲线饱满，滞回环形状一致。增大楔率，试件EDB-2A、EDB-2B、EDB-2C的承载力和刚度依次降低，但变化不明显。主要是因为EDB-2支撑耗能板长细比较大，改变楔率之后，应力分布仍较均匀。从EDB-2骨架曲线可以看出，EDB-2系列支撑的轴向承载力随楔率的增加而降低,主要是因为耗能板局部横截面随楔率的增加而减小所致。EDB-2系列试件刚度退化曲线形状接近，呈现初步降低趋势，EDB-2A、EDB-2B、EDB-2C试件的初始轴向刚度分别为20.00、17.96、16.79 kN/mm。当耗能板楔率改为0.33时，初始刚度降低10.2%，当耗能板楔率改为0.60时，初始刚度降低16.05%。

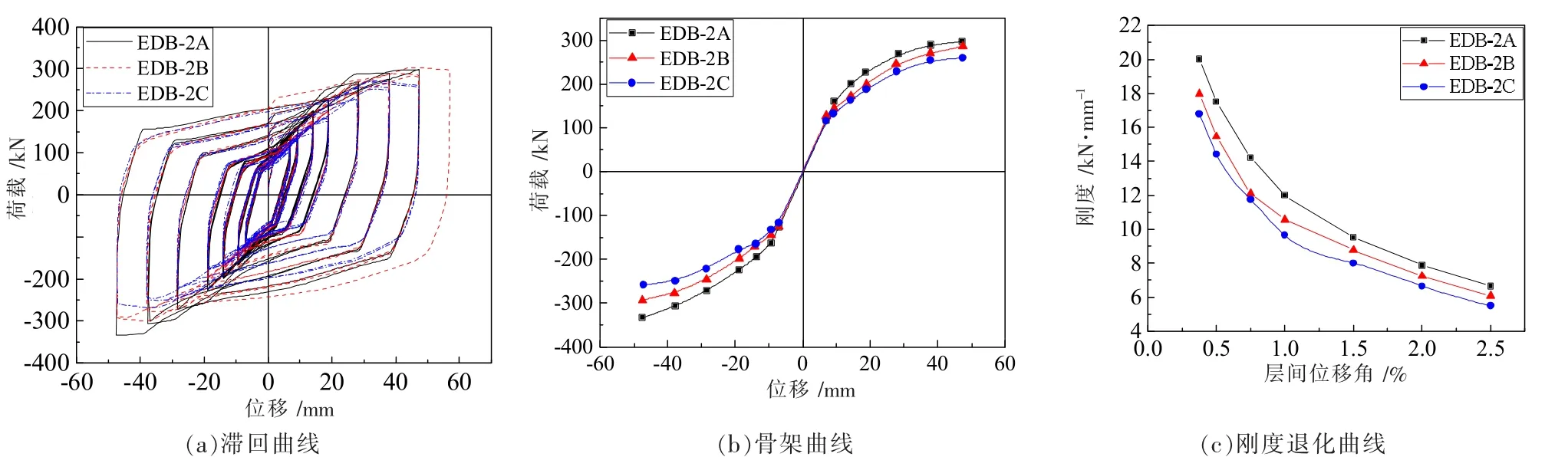
图11 EDB-2系列支撑

4.1.3 EDB-3系列支撑

EDB-3系列支撑耗能板为两段式耗能板，在同一根耗能板上既有受压段又有受拉段。从图12可以看出，EDB-3系列试件的滞回曲线饱满，试件滞回环形状基本相同。改变楔率，试件EDB-3A、EDB-3B、EDB-3C早期的承载力和刚度随楔率的增加依次降低。增大楔率之后，EDB-3B和EDB-3C变形能力降低，最大变形到层间位移角为1%处。主要原因是耗能板横截面宽度较小，易发生面内侧向屈曲变形致使耗能板失去承载能力。EDB-3系列试件刚度退化曲线前期下降趋势大致相同，EDB-3A，EDB-3B，EDB-3C试件的初始轴向刚度如下，依次为40.9、38.5、35.8 kN/mm。耗能板楔率改为0.33，初始刚度降低5.8%，耗能板楔率改为0.60，初始刚度降低12.5%。可见，过分增大楔率会使EDB-3系列支撑提前破坏，进而影响支撑的变形能力和耗能能力。

图12 EDB-3系列支撑

以上三种耗能板改变楔率的结果分析可知，改变楔率对支撑承载力和刚度有降低作用，对EDB-1作用显著，对EDB-2和EDB-3影响较小。改变楔率，使得耗能板的应力能够从中间变截面处向两边均匀分布。但由于EDB-3耗能板宽度较小，过分增大楔率会使EDB-3系列支撑提前破坏，楔率不适宜增加过大。

4.2 耗能板布置方式的影响

由图13可知，EDB-1A与EDB-2A试件滞回曲线、骨架曲线和刚度退化曲线，变化不大。承载力EDB-2A较EDB-1A略大，初始刚度EDB-2A较EDB-1A略低，中后期EDB-2A刚度超过EDB-1A。EDB-3A承载力最大，初始刚度最大，在层间位移角为1.5%时支撑轴向承载力最大，加载后期，承载力逐渐减小，骨架曲线呈反S型。EDB-1A，EDB-2A，EDB-3A试件的初始轴向刚度分别为19.96、17.21、40.99 kN/mm。可见，在三种耗能板布置方式中，EDB-3A布置方式下的支撑承载能力和变形能力最优。

图13 EDB-1A、EDB-2A、EDB-3A试件

由于EDB-1A支撑耗能板对称布置，上部耗能板先进入塑性耗能，导致上部耗能板会先发生塑性破坏，由于耗能板较短，耗能板更易发生受压破坏。EDB-2A支撑在加载后期，多波屈曲段易集中发生在耗能板端部处，从而发生破坏，从骨架曲线可以看出EDB-2A支撑受拉承载力高于受压承载力，由于耗能板较长，耗能板更易发生拉断。EDB-3A支撑两段式耗能板上一段受压一端受拉，由于耗能板宽度较小，长细比较大，在拉压过程中，耗能板上部受拉段更易发生破坏。EDB-3A支撑在破坏前承载力缓慢下降，有明显的破坏预兆，属于延性破坏。

4.3 等效粘滞阻尼比

等效粘滞阻尼比能够有效评估支撑的耗能能力，准确反映结构的损伤程度。本文等效粘滞阻尼比是按式（1）计算，即

SAEDFA为某一幅值下滞回环面积（见图14），A、D为该幅值下最大位移点。

图14 等效粘滞阻尼比示意图

图15为各模型的等效粘滞阻尼比与位移的曲线图。各模型等效粘滞阻尼比随位移的增大总体为上升趋势。EDB-1A、EDB-3A支撑等效粘滞阻尼比均能达到0.5，EDB-2A支撑等效粘滞阻尼比均能达到0.4，说明双层方钢耗能支撑滞回性能良好，耗能能力优越。增加楔率后，EDB-1系列，EDB-2系列支撑粘滞阻尼比增加，表明增加楔率能够提高双层方钢耗能支撑的耗能能力。增加楔率后，EDB-3系列支撑由于耗能板易提前发生破坏，等效粘滞阻尼比降低，耗能能力降低。综上，合理设计耗能板楔率能够有效提高支撑的耗能能力。

图15 等效粘滞阻尼比-层间位移角曲线

5 设计方法

以EDB-2A为例，参考相关文献，给出双层方钢耗能支撑承载力计算公式和方钢厚度计算公式。

5.1 支撑承载力计算

参考文献[18]，根据边界条件将双层方钢耗能支撑耗能板的稳定性问题转化为双向均匀受压的四边简支板的稳定性问题，在板的两边每单位宽度上均布压力Px和Py，耗能板计算模型见图16。

图16 耗能板计算模型图

当耗能板屈曲变形与方钢接触时，设Py=γPx，当耗能板屈曲变形与方钢未接触时，Py为零。根据耗能板弹性屈曲分析[19]，得到耗能板的临界屈曲荷载为

式中，γ未知，需通过波峰挤压力求得。如图17所示，双层方钢耗能支撑在轴力作用下，耗能板会发生多波屈曲变形，半波长为Lc。从中取出一段波进行分析，在上部一侧耗能板受到轴压力P，挤压反力Nr/2，这两个力合力为Pβ，三个力的关系如下

图17 耗能板对方钢挤压示意图

则耗能板对方钢的挤压力Nr可得

上式中，Nr为耗能板对方钢的挤压力，P为耗能板所受轴压力，β为屈曲波与水平方向的夹角。根据图17中的三角关系可得

式中，δ为耗能板与外方钢之间的初始空隙；υp为耗能板泊松比；εc为耗能板在轴压力作用下的轴向应变，P＞0为正，P＜0为负；tc为耗能板的厚度。

耗能板在塑性阶段时，假设耗能板的材料本构关系为双线性模型，且第二刚度Et=αE，则轴压力将式（6）、（5）代入式（4），求得耗能板对外方钢在波峰出的挤压力

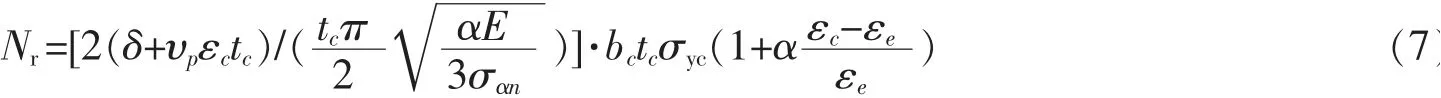
求得γ为

耗能板沿板宽度y方向只能形成一个半波长，式（2）中n取1。将式（8）及lc=l/m代入式（2），由∂Px∂m=0，求得m值，进而得到Px的最小值，即为耗能板的临界屈曲荷载由于存在两个耗能板受压屈曲，两根耗能板受拉屈服，因此，支撑整体承载力

式中，n为耗能板段数。

屈服承载力有限元结果与理论计算结果对比如表3所示。由表可知，有限元模拟得到的屈服承载力与理论公式计算结果吻合，表明理论计算公式具有较高的准确性。

表2 屈服承载力对比

5.2 方钢厚度计算

为防止外方钢受挤压发生局部鼓曲而导致支撑的承载力下降，本文给出了双层方钢耗能支撑内外方钢的设计方法。其示意见图18。

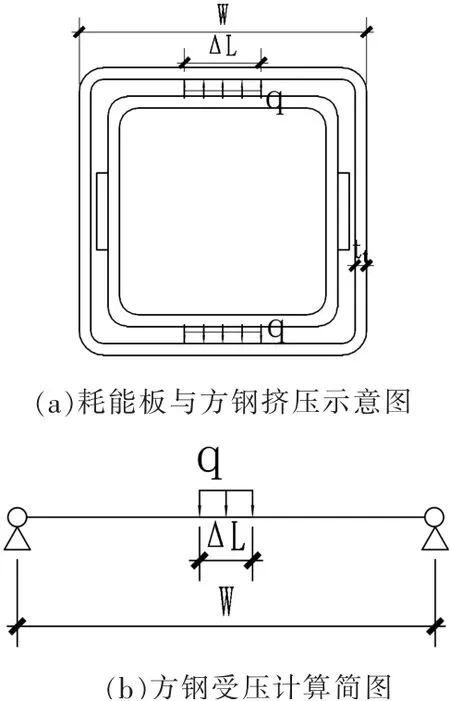
图18 耗能板与方钢的挤压图

根据剪力为零的原则，求得受压截面上的弯矩为

式中，W为方钢截面边长；ΔL为耗能板与方钢接触段的宽度；q为耗能板与方钢接触段截面的宽度。

有限元分析表明，方钢鼓曲范围约为屈曲半波的长度，因此假设方钢对耗能板的约束距离为沿长度方向上的屈曲半波长度Lc，则方钢受压段所能承受的最大塑性弯矩为

式中tt为方钢厚度；σyt为方钢的屈服应力。

当弯矩达到最大塑性弯矩时，方钢发生鼓曲破坏，此时，方钢破坏的临界荷载为

当方钢波峰处挤压力Nr=Pcr时，将式（7）和式（13）代入上式，可得方钢厚度为

有限元模拟中支撑方钢厚度均为6 mm，模拟结果发现EDB-1A、EDB-1B、EDB-2A、EDB-2B、EDB-3A等支撑外方钢存在鼓曲现象，如下图19所示，下图以EDB-1A方钢鼓曲图为例展示。经过式（14）计算，EDB-1A、EDB-2A支撑方钢厚度理论值为7.53 mm，建议设计值取8 mm；EDB-1B、EDB-2B、EDB-3A支撑方钢厚度理论值为6.52 mm，建议设计值取7 mm；EDB-1C、EDB-2C、EDB-3B、EDB-3C支撑方钢厚度理论值分别为5.95、5.58、5.05 mm，建议设计值取6 mm。

图19 方钢鼓曲图

6 结论

（1）双层方钢耗能支撑的滞回曲线饱满且稳定，具有良好的承载能力和变形能力。

（2）耗能板布置方式对支撑的承载力、刚度、耗能能力影响较显著。内置八根耗能板对称布置的支撑相对于内置一段式耗能板的支撑承载力和刚度略高，但变化不明显。内置为两段式耗能板的支撑承载力最高，变形能力和耗能能力相对最优。

（3）通过合理设计耗能板楔率能够有效提高双层方钢耗能支撑的耗能能力；楔率过大，耗能板提前破坏，支撑较早破坏。给出了双层方钢耗能支撑的屈服承载力和方钢厚度的计算公式,与有限元结果对比吻合。