钢筋混凝土历史建筑中方钢-混凝土的极限粘结应力分析

糜镇东，淳庆，金辉

(东南大学 建筑学院，江苏 南京 210008)

近代时期，钢筋混凝土结构技术由西方传入中国并大量应用于各大城市建设中.目前，保留下来的钢筋混凝土历史建筑大量存在于北京、上海、武汉、天津、青岛、西安、厦门、广州、济南、南京、杭州等大中型城市中.这些钢筋混凝土历史建筑是中国城镇建筑遗产的重要组成部分，具有重要的历史价值、艺术价值、科学价值和社会价值.而近代钢筋混凝土建筑中使用最为广泛的方钢在形状与构造方面明显不同于现代圆钢，因而其粘结滑移性能与现代圆钢也有明显不同.

粘结滑移性能是评判钢筋混凝土结构的承载性能和变形性能的重要指标[1].现代圆形钢筋与混凝土之间的粘结滑移关系主要通过拉拔实验、梁式实验与轴拉实验3种实验方式进行研究.Lutz等[2]通过钢筋与混凝土的拉拔实验，提出钢筋与混凝土之间的粘结力主要由化学结合力、摩擦力与机械咬合力3个部分组成.国内外学者大量研究表明，钢筋的直径、肋间距、肋的形状对粘结应力有决定性作用，且肋的形状决定了裂缝大小和最终的破坏模式[3-5].另外，混凝土的抗拉强度和钢筋的屈服强度也是钢筋混凝土极限粘结应力的重要影响因子[6-7].

上世纪60年代至今，国内外学者提出了大量现代圆形钢筋与混凝土的粘结滑移理论模型.早在1977年，Orangun等[8]就通过实验得出带箍筋的钢筋混凝土粘结应力的表达式；Darwin等[9-10]拟合了带箍筋和不带箍筋的钢筋混凝土粘结应力表达式并进行验证；在此基础上，Harajli[11-12]对高强混凝土、普通混凝土等劈裂破坏形式的粘结滑移公式进行推导.目前仅有少数关于近代方钢-混凝土粘结性能的试验研究.张时琦[13]对近代方钢进行拉拔实验，根据现代的混凝土规范，拟合粘结应力四段折线图，并且根据该本构模型对近代钢筋混凝土梁进行ANSYS有限元模拟分析.Chun等[14]搜集整理了近代民国关于钢筋混凝土规范的资料，并对近代钢筋进行本构关系的实验研究，得出近代钢筋的本构模型，总结近代钢筋的大致尺寸形制，研究近代时期常用的方钢、螺旋钢、扁截钢的力学特性.

综上所述，目前关于钢筋混凝土的粘结滑移性能研究主要针对现代圆钢，而关于近代方钢-混凝土粘结滑移计算模型的研究鲜有报道.因此，本文对近代钢筋混凝土结构中的方钢-混凝土极限粘结应力的计算模型进行研究.

1 近代文献关于方钢-混凝土的粘结性能规定

近代文献规定的方钢-混凝土极限粘结应力的安全值[15-27]，如表1所示.表1中：τ为方钢-混凝土的极限粘结应力；fcu，fct分别为混凝土的抗压强度和抗拉强度；fc，28 d为混凝土养护28 d后抗压强度；ftr为混凝土的抗拉强度设计值.近代时期，国内工程界对混凝土配比的使用较为单一，大多混凝土配比为V(水泥)∶V(砂子)∶V(石子)=1∶2∶4，V为体积，《钢筋混凝土学》[24]规定湿拌法的混凝土用水量(质量)为干料总质量的10%～13%.因此，近代时期的混凝土抗压强度相对固定，浇筑28 d后的抗压强度为14.00～16.46 MPa；而混凝土的设计值通常取安全系数为3～5，较为保守[24].

表1 近代文献规定的方钢-混凝土粘结应力的安全值Tab.1 Safety values of bond stress of square rebar-concrete regulated in modern literatures

近代中国工程界明确了方钢-混凝土之间的粘结力主要由混凝土对钢筋握裹作用产生的摩擦阻力和方钢表面粗糙不平的机械咬合力组成；方钢-混凝土粘结滑移极限应力安全值约为0.5～0.8 MPa，当混凝土中的水泥体积比小于常用配比(V(水泥)∶V(砂子)∶V(石子)=1∶2∶4)时，应该对安全粘结力进行酌减，当水泥体积比大于常用比例时，可对安全粘结力进行酌增[16-17，19-20，23].

参考文献[28]，结合课题组完成的数十个近代方钢-混凝土建筑的检测评估结果，可以认为近代混凝土强度等级为C15.依据GB 50010-2010《混凝土结构设计规范》[27]，近代混凝土轴心抗压强度标准值为10 MPa，其抗拉强度标准值ftk为1.27 MPa，轴心抗拉强度特征值ftr为0.91 MPa，因此，近代方钢-混凝土的极限粘结应力设计值应为2.73 MPa.由此可见，近代时期虽对方钢-混凝土间的粘结滑移性能有一定的认识，但其设计强度过于保守，近代方钢-混凝土极限粘结应力的设计安全值约为现行规范下设计值的0.19～0.29倍.

2 方钢-混凝土粘结性能的理论模型

目前，钢筋混凝土粘结性能的理论模型均是针对圆形截面的钢筋类型，不适用于方钢-混凝土的粘结性能分析.因此，基于近代方钢的构造特征，推导近代方钢-混凝土的粘结性能理论计算模型.

方钢形状简化图，如图1所示.劈裂破坏时的应力分布，如图2所示.图1，2中：α为混凝土破坏面与方钢表面的夹角；Rr为径向应力；F为摩擦力；P为压应力；R为合力；μ为摩擦系数.当方钢与混凝土之间产生相对滑移时，方钢与混凝土表面会产生相对的滑移力，方钢与混凝土之间由于产生了相对滑移，从而产生了新的作用面.方钢和混凝土发生相对滑移直至混凝土界面破坏的过程中，理想的简化模型将方钢视作锥形体[29]，且混凝土破坏面覆盖方钢表面的肋间距，此时，混凝土破坏面与方钢表面的夹角为α.在理想简化模型中，方钢与混凝土间的粘结力全部由混凝土与方钢之间的摩擦力提供.

图1 方钢形状简化图 图2 劈裂破坏时的应力分布Fig.1 Simplified diagram of rebar shape Fig.2 Stress distribution at splitting failure

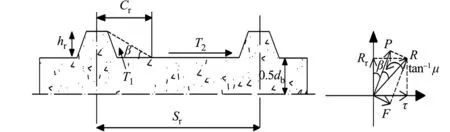
图3 混凝土劈裂实际破坏面Fig.3 Actual failure surface of concrete splitting

国内外学者以该理想简化模型为基础进行研究发现，混凝土实际破坏时的界面角度并不是α，混凝土也无法完全覆盖方钢表面肋间距.在混凝土劈裂破坏时，破坏界面会形成一个楔形面[30]，如图3所示.图3中：hr为方钢的肋高；Cr为楔形面底边顶点到肋的距离；Sr为肋间距；db为方钢边长；T1为楔形面提供的拉拔力；T2为水平面的摩擦力.在方钢混凝土劈裂破坏的瞬间，极限粘结应力主要由楔形面给予方钢的拉拔力T1和楔形块之外的方钢表面与混凝土的摩擦力T2提供，除此之外，还有混凝土浇筑时产生的化学吸附力T3[31].

由于方钢与圆钢的截面形状不同，导致方钢与混凝土之间的握裹力与劈裂力的计算方法不同，使得方钢与混凝土之间的粘结力与拉拔力计算方法不同[30].对于方钢的径向应力做如图2所示的简化处理.因此，根据混凝土破坏时的实际劈裂面，取一个肋间距Sr进行分析，可以推导得到破坏的楔形面上混凝土与方钢的粘结应力τ1与径向应力Rr的关系，即

(1)

式(1)中:β为假想的肋平面的倾斜角.

同时，方钢总粘结应力τ与总拉拔力T存在关系为

(2)

式(2)中:lb为所取计算长度中方钢的有效长度.

对照Wang[30]给出的公式，将圆钢的理论模型加以改进，并考虑方钢与混凝土的化学吸附力.方钢在拉拔过程中，混凝土会给方钢一个握裹力，假设方钢会在劈裂时刻劈裂为两半(图2)，则劈裂时刻的楔形面部分的劈裂力Fsplit，1表示为

(3)

方钢混凝土的总劈裂力Fsplit表示为

Fsplit=fctAsplit.

(4)

式(4)中:Asplit为混凝土的有效劈裂面积.

根据式(1)～(3)，可得

T1=4Fsplit，1tan(β+arctanμ)=4Crfctlsplittan(β+arctanμ).

(5)

式(5)中:lsplit为混凝土劈裂部分的长度.

水平面的摩擦力T2除去倾斜角β，可表示为

T2=4μFsplit，2=4μ(Sr-2Cr)fctlsplit.

(6)

式(6)中:Fsplit，2为方钢水平面部分的劈裂力.

可以得到该肋间距中的楔形面与水平面的总拉拔力T为

T=T1+T2=4Fsplit，1tan(β+arctanμ)+4μFsplit，2.

(7)

将式(6)化简，可得

(8)

根据拉拔力与粘结应力的关系，可以得出楔形面与水平面的总平均粘结应力τ1+τ2为

(9)

参考Martin[31]的建议，化学吸附力产生的粘结应力τ3取值为0.04fcu.总粘结应力可表示为

(10)

表2 各文献的摩擦系数取值Tab.2 Values of friction coefficients in various literatures

3 方钢-混凝土粘结应力理论模型

方钢-混凝土的粘结应力与其摩擦系数有关.不同文献的摩擦系数取值，如表2所示.综合表2中各文献摩擦系数的平均值，取方钢与混凝土的摩擦系数μ为0.41进行后续分析.

表3 文献[13]和[36]试件极限粘结应力的试验值和理论计算值对比Tab.3 Comparison between experimental value and theoretical calculation value of bond stress of specimens in literature [13] and [36]

根据表3中所得数据绘制散点图，得到粘结应力理论计算值与试验值的对比图，如图5所示.图5中：k为斜率.由图5可知：16个散点数据中有5个数据点明显偏离了斜率(100±15)%的包络线，积分误差绝对值(IAE)为15.8%.此外，利用文中提出的理论公式得到的极限粘结应力的平均计算值与平均试验值之比为1.08，证明该理论公式计算得出的方钢-混凝土极限粘结应力具有较高的准确性.

图4 试件劈裂情况 图5 理论计算值与试验值对比Fig.4 Situation of specimen splitting Fig.5 Comparison between theoretical values and experimental values

4 参数分析

方钢-混凝土的粘结应力主要与方钢-混凝土的摩擦系数、方钢的肋间距和肋高、混凝土的抗拉强度和抗压强度及最终破坏的裂缝长度有关.从式(10)可以看出，混凝土相关强度参数越大，方钢-混凝土的粘结应力也越大.但是，方钢的肋间距Sr、肋高hr及方钢边长db和摩擦系数μ对粘结应力的影响并不能在公式中直观地体现.因此，分析这4个参数对极限粘结应力的影响程度.

4.1 摩擦系数

选取表3中的5号试件进行参数分析(下同)，摩擦系数的取值范围为0.2～0.6，其余参数不变.摩擦系数对极限粘结应力的影响，如图6所示.

由图6可知：摩擦系数对极限粘结应力的影响几乎呈线性增长，摩擦系数越大，极限粘结应力就越大；当摩擦系数从0.2增长至0.6时，极限粘结应力从4.78 MPa增长至11.73 MPa，即摩擦系数增长到原来的3倍，极限粘结应力增长了145%.因此，摩擦系数对方钢-混凝土粘结性能的影响较为显著.

4.2 方钢的肋间距

方钢的肋间距的取值范围为20～40 mm，其余参数不变，得到方钢的肋间距对极限粘结应力的影响，如图7所示.由图7可知：方钢的肋间距对极限粘结应力的影响呈反比例关系，肋间距越大，极限粘结应力越小；当方钢的肋间距增长20 mm，即当方钢表面肋间距增长到原来的2倍，极限粘结应力仅仅减小了11%.因此，方钢的肋间距对方钢-混凝土粘结性能的影响较小.

图6 摩擦系数对极限粘结应力的影响 图7 方钢的肋间距对极限粘结应力的影响 Fig.6 Influence of friction coefficient on ultimate bond stress Fig.7 Influence of rib spacing of square rebar on ultimate bond stress

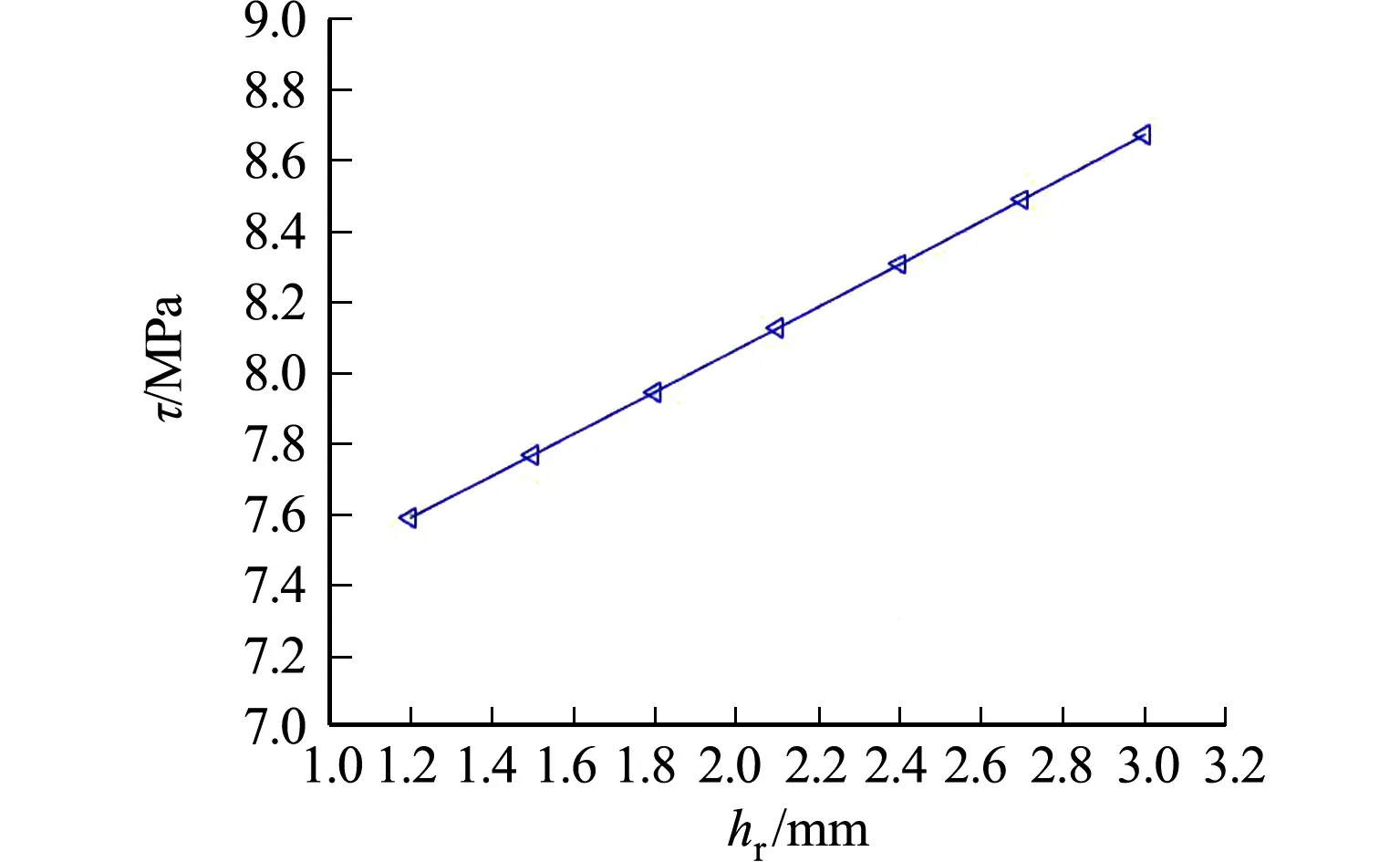
图8 方钢的肋高对极限粘结应力的影响Fig.8 Influence of rib height of square rebar on ultimate bond stress

4.3 方钢的肋高

方钢肋高取值范围为1.2～3.0 mm，其余参数不变，方钢的肋高对极限粘结应力的影响，如图8所示.

由图8可知：方钢的肋高对极限粘结应力的影响与摩擦系数相仿，都是呈线性变化，且随着方钢肋高的增加，极限粘结应力也随之增加，但是与摩擦系数稍有不同的是，方钢肋高对极限粘结应力的影响并不是很大，由于近代方钢的肋高大多为2 mm[14]，即使肋高在1～3 mm之间变动，劈裂时粘结应力的变化也不会超过1.2 MPa；且当肋高增大到原来的2.5倍，粘结应力仅增长了13%.

4.4 方钢边长

方钢边长的取值范围为6～26 mm，其余参数不变，方钢边长对极限粘结应力的影响，如图9所示.由图9可知：方钢边长对劈裂时试件的极限粘结应力的影响呈反比例关系，方钢边长越大，极限粘结应力越小，当方钢边长扩大到24 mm时，试件劈裂时产生的极限粘结应力降低至原来的30.4%.

综上所述，摩擦系数和方钢的肋高与方钢-混凝土极限粘结应力均呈线性关系，且均为正比例关系，其中，摩擦系数对粘结滑移性能的影响较大，方钢的肋高对粘结滑移性能的影响较小.方钢的肋间距及方钢边长与方钢-混凝土极限粘结应力呈反比例关系，肋间距越大，极限粘结应力越小，但影响程度偏小.而方钢边长对方钢-混凝土劈裂时的极限粘结应力的影响相对肋间距来说更大，且方钢边长db<16 mm时对极限粘结应力的影响较方钢边长db>16 mm时的影响更大.

4.5 近代方钢-混凝土粘结性能与现行规范的比较

近代历史文献采用安全值的方法规定方钢-混凝土的极限粘结应力为0.5～0.8 MPa.我国现行国标GB 50010-2010《混凝土结构设计规范》[27]建议用四段式折线(粘结滑移曲线，粘结应力为纵坐标，相对滑移值为横坐标)表示方钢-混凝土的粘结性能，采用3个特征点确定四段折线，分别为(0.025Scr，2.5ftr)，(0.040Su，3.0ftr)，(0.550Sr，ftr)，其中，Scr为劈裂段的最大相对滑移；Su为失效阶段的最大相对滑移；Sr为残余段的最小相对滑移.可见现行的混凝土规范对极限粘结应力的规定仅与混凝土的强度有关.取近代混凝土立方体强度抗压标准值15 MPa，则现行规范规定的方钢-混凝土极限粘结应力为2.73 MPa.

根据上文的参数分析，取方钢的肋高为2.0 mm，摩擦系数为0.41，混凝土试块边长为160 mm且假设破坏时混凝土试块截面均劈裂，方钢肋间距的取值范围为20～44 mm，方钢边长取12～26 mm，计算得到方钢-混凝土的极限粘结应力理论值为4.69～11.83 MPa.对比表1中的数据可知，近代文献和现行规范对极限粘结应力设计值的规定都相对保守，尤其对于近代文献规定值来说，极限粘结应力规定的最大值约为理论计算最小值的0.17倍.

5 结论

对近代历史文献中方钢-混凝土粘结性能的相关规定进行整理分析，基于方钢的构造特征，提出方钢-混凝土极限粘结应力的理论计算模型，得出以下3点结论.

1) 近代中国历史文献中规定的极限粘结应力非常保守，约为现行混凝土规范中规定的同等级混凝土与带肋方钢的极限粘结应力的0.19～0.29倍.

2) 依据方钢-混凝土粘结滑移性能的楔形截面破坏理论，文中提出的方钢-混凝土极限粘结应力的计算方法的理论计算值与试验值的平均比值为1.08，IAE为15.8%，证明理论公式的准确度较高.

3) 影响近代方钢-混凝土极限粘结应力的因素主要为混凝土与方钢的摩擦系数，方钢的肋间距、肋高和边长；摩擦系数和方钢的肋高对于极限粘结应力的影响为正相关，其中，摩擦系数的影响较大；方钢的肋间距和方钢边长对极限粘结应力的影响为负相关，其中，方钢边长的影响较大.