带辅助支承的传动杆动态特性试验和仿真

娄 鹏，张 涛，章焕章

（中国航发商用航空发动机有限责任公司，上海 200241）

0 引言

大型客机发动机径向传动杆（Radial Drive Shaft，RDS）负责将功率由高压转子传递至转接齿轮箱，其结构具有大长径比特征，为了提高临界转速，通常需要在中间位置添加辅助支承；内杆、外杆和齿轮轴之间通过浮动花键连接。该传动杆的动态特性尤其是临界转速与刚性连接的发动机主转子特性显著不同，当工作转速靠近或高于临界转速时，转子振动迅速增大，极易引发传动杆碰摩和轴承、花键磨损等故障。

梅庆等的理论和试验研究表明，浮动花键连接结构的临界转速受花键连接刚度影响极为显著，其中变化较为剧烈的第2阶段连接刚度一般需要通过试验确定；陈聪慧利用部件试验修正了花键连接刚度，并将修正后的刚度值应用到整机传动杆组件的临界转速计算中；郭梅等、吴凡等通过试验测试出临界转速，进而修正出合适的花键连接刚度。上述研究要么对象为单杆传动，要么仅测试了轴承座处的加速度响应，而带辅助支承传动杆的动态特性试验研究还有待深入，例如传动杆位移响应和轴承座加速度响应之间的联系，传动杆进入临界转速后的振动特性，均尚不清楚。

因传动杆磨损等故障频发，中国在传动杆临界转速的仿真方面也开展了大量工作。吴凡等针对大长径比航空发动机中央传动杆存在的装配状态较差、同轴度不理想等问题，提出大长径比中央传动杆转子动力学设计应同时考虑花键套齿联轴器的横向刚度和角向刚度；郭霞等的研究表明，要准确计算径向传动杆的临界转速，边界条件的选取和简化是关键，采用整体模型得到的计算结果与模态试验结果较为一致，但文中将花键连接处理为固定连接；洪杰等、王正、程小勇、欧园霞等、晏砺堂等均指出，支承刚度是影响转子动态特性的重要因素；杜佳佳等在计算传动杆临界转速时采用了根据工程经验得到的支承刚度。但是上述研究均忽略了轴承座等部件的结构特征，因而不能预警传动杆以外的部件共振。国外在这种带辅助支承的大长径比传动杆上的研究活动主要集中在各发动机公司，近年未见公开发表的研究成果。

本文通过搭建带辅助支承的径向传动杆试验台，测量了传动杆横向位移和轴承座加速度响应。根据多台份试车经验和故障形式提出了“试车临界转速”的概念，并将“仿真临界转速”和“试车临界转速”进行了对比验证。

1 传动杆动态特性试验

1.1 试验台搭建

试验件主要由内、外2根传动杆组成，通过花键传扭，内传动杆与增速箱高速轴内花键相连，外传动杆与减速箱低速轴外花键相连，中间轴承支撑在辅助轴承座上。试验时测量试验件转速、内外传动杆中点位移、3处轴承座加速度和滑油压力、温度和流量等。试验台结构形式和传感器粘贴位置如图1所示，传动杆组件实物如图2所示。图中较粗的为外杆，与转接齿轮箱（Transfer Gear Box，TGB）相连，中央传动齿轮箱（Internal Gear Box，IGB））的轴承座（IGB Support，IS）、辅助支点轴承座（Assisstant Suppprt，AS）和转接齿轮箱轴承座（TGB Support，TS）。

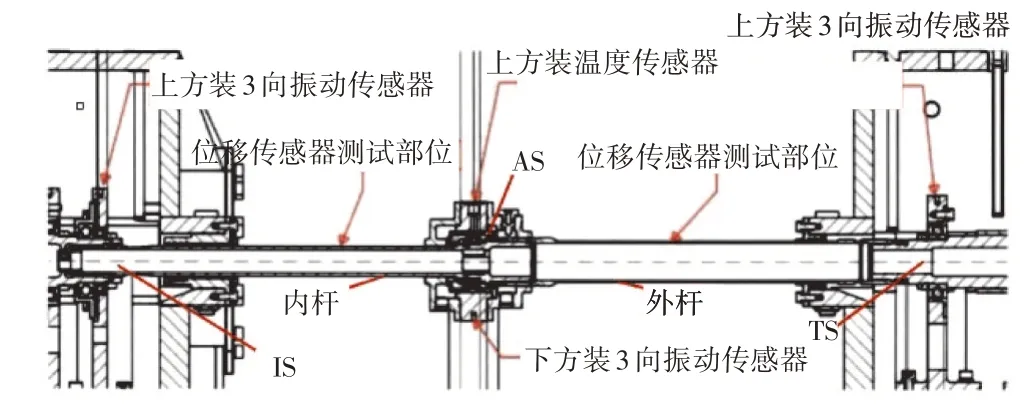
图1 试验台结构形式和传感器粘贴位置

图2 传动杆组件实物

根据初步的临界转速计算，将试验研究分为2个阶段，第1阶段最高转速为26000 r/min，用于摸索传动杆临界转速，研究位移和加速度响应随转速的变化规律；第2阶段最高转速为29000 r/min，用于研究传动杆发生弯曲共振后继续增大转速时的动力学响应特性，判断该临界转速能否快速通过。

1.2 第1阶段的振动测试和特性分析

试验第1阶段先将转速缓慢拉升至最高转速26000 r/min，再快速降低至0。所测试的内、外传动杆位移响应总量随转速的变化曲线如图3所示，测点的加速度随转速的变化曲线如图4所示。各图均采用双纵坐标，其中绿色曲线为转速信号参考右侧纵坐标系，剩余曲线参考左侧纵坐标系，并且方向为水平方向，方向为垂直方向，方向与传动杆轴向平行。

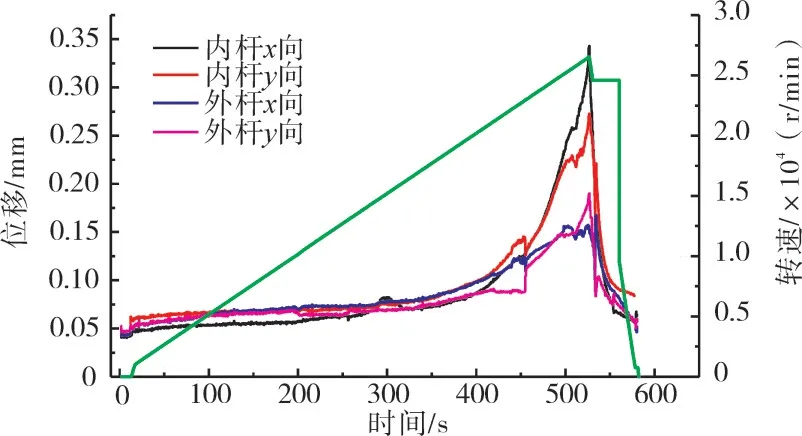
图3 第1阶段传动杆位移随转速的变化曲线

通过对比图4（a）、（b）、（c）归纳出带辅助支承的传动杆组件具有以下动态特性。

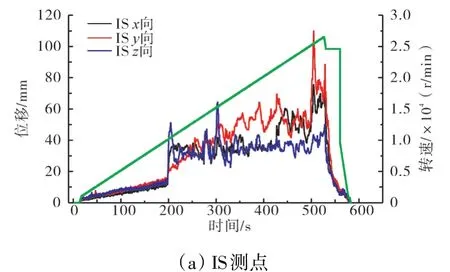
图4 第1阶段不同测点的加速度随转速的变化曲线

（1）当转速升至某特定值时，位移和加速度均快速增大。例如：内杆向位移由第350 s时的0.075 mm快速增大至第520 s的0.35 mm，增幅为450%；AS轴承座轴向加速度由第450 s时的10增大至第520 s的60，增幅为600%。可以判定发生了共振而不是受迫响应。

（2）各部件都有共振被激起的可能性。例如：在23000 r/min附近发生了AS轴承座轴向共振，在26000 r/min附近则发生了传动杆弯曲共振。

（3）发生弯曲共振时，内杆振动大于外杆振动，说明本次试验的主要矛盾是内杆。

（4）对比内杆、向位移和AS轴承座各向加速度响应幅值变化规律可以发现，内杆位移响应的增大在时间上早于加速度的增大，位移响应增大一段时间后加速度响应才开始显著增大，但是加速度增速更快。也就是说，传动杆位移共振先于轴承座加速度共振，并且增速慢、转速区间跨度大。

1.3 第2阶段的振动测试和特性分析

梅庆等的试验结果表明，弹性联轴器的位移响应共振带很宽，振动在经历了很长过程的增大之后才显著减小至非共振状态，转速区间跨度可达5000 r/min左右。但该规律是否适用于径向传动杆还有待验证。

第2阶段的最高转速为29000 r/min，测量的内、外传动杆位移响应总量随转速变化曲线如图5所示，测点的加速度响应曲线如图6所示。

图5 第2阶段传动杆位移随转速变化曲线

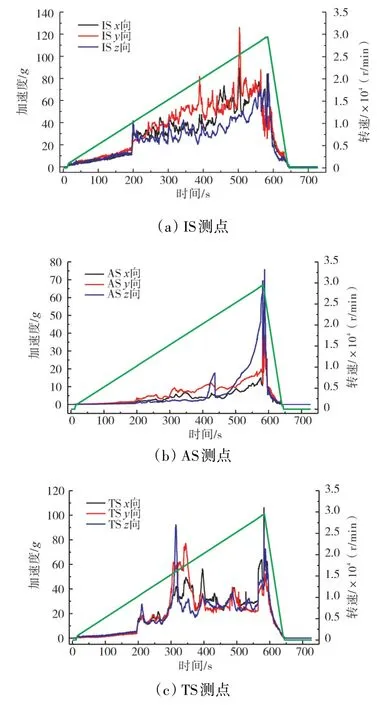
图6 第2阶段不同测点加速度随转速的变化曲线

从图5、6中可见：

（1）传动杆位移响应和AS加速度响应均继续增大，共振继续增强。

（2）在传动杆发生弯曲共振后，浮动花键进入非正常连接状态，共振峰起峰速度更快。

上述现象表明，通过浮动花键连接的径向传动杆振动具有显著的非线性特性。在进入共振区后，振动响应持续增大，并且共振区间跨度很大。这与一般刚性转子通过临界转速后振动迅速减小有明显区别。因此，如果试车时发生传动杆弯曲共振，采用继续拉升转速来通过临界转速的方法行不通。

1.4 试车临界转速的判定

如前所述，传动杆发生弯曲共振后振动响应仍然会持续增大，共振区间可达3000～5000 r/min；另外，在整机试车时，受结构空间限制，不能监测传动杆位移响应的幅值和相位变化规律，无法直接判断共振是否发生，能获取的测试信号只有轴承座等位置处的加速度响应，因此，如何在整机试车时确定试车临界转速也是传动杆动态特性研究的难题。

由第1.2节的试验测试和分析结果可知，当轴承座加速度响应开始起峰时，传动杆位移响应已经更早起峰，只是增长幅度较慢，也就是说当轴承座加速度信号表现出共振特性时，传动杆已经发生了弯曲共振。

从故障模式的角度来看，在某型发动机整机试验的一次起动中，在相对换算转速为72.7%时，各测点的振动总量处于正常水平，振动情况良好；当相对换算转速升高到75.0%时，振动总量突增，中介机匣垂直测点的振动总量幅值从13突增到40以上，增幅约为300%，并引发了花键磨损故障。虽然传动杆进入共振状态后振动响应会继续增大，但加速度增幅为300%时已经很容易引发花键磨损，该转速之后的振动恶化更不能接受。

因此，本文尝试对传动杆共振给出量化定义：在较短的转速变化区间（一般小于10%）内，如果轴承座加速度振动总量增至300%及以上时，可判定传动杆发生了横向弯曲共振，这种振动极易引发传动杆碰摩或花键磨损等故障，该转速即为传动杆的试车临界转速。根据该定义，当临界转速裕度大于10%时，传动杆振动响应幅值只有危险幅值的1/3甚至更小。

以第1阶段试验为例，根据AS轴承座轴向加速度响应总量，取第480.7 s时的振动值为基准，转速为24226 r/min，加速度响应值为10.1；在第508.7 s时，转速为25624 r/min，加速度响应值为31.9。虽然转速只增大了5.8%，但加速度共振响应总量增大至316%，判断该转速25624 r/min为试车临界转速。

2 传动杆动态特性仿真分析

2.1 传动杆组件有限元建模

传动杆组件动态特性试验研究表明，在转速升高过程中，不仅发生了传动杆弯曲振动，还发生了轴承座部件共振。杜佳佳等的研究表明，陀螺力矩对传动杆临界转速计算影响极小，因此，带辅助支承的径向传动杆动态特性尤其是临界转速的计算可以转化为综合考虑轴承座结构特征、轴承支承刚度和花键连接刚度的系统模态求解。

将花键特征简化为齿根圆柱面，简化后的几何模型和轴承编号如图7所示。采用四面体网格划分的有限元模型（如图8所示）约束轴承座底面位移。

图7 传动杆部件几何模型

图8 传动杆部件有限元模型

2.2 轴承支承和花键连接建模

基于Workbench，采用Bushings单元对棒轴承和球轴承支承刚度建模，轴承支承刚度具体数值见表1。

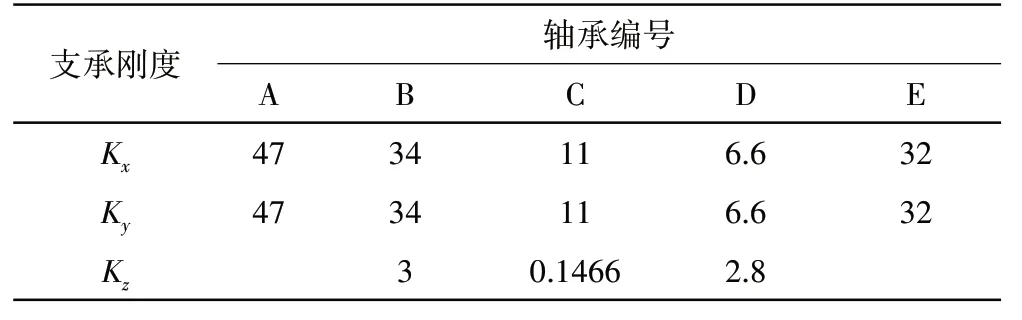
表1 轴承支承刚度 ×104 N/mm

用Bushings单元连接外花键面和内花键面，并且径向刚度设置为1×10N/mm，角向刚度设置为2×10N·mm/rad，圆周方向的啮合刚度设置为1×10N·mm/rad。

2.3 模态求解和临界转速对比

模态求解得到传动杆组件的典型低阶振型如图9所示。图9（a）为辅助支承轴向振型，振动频率为357 Hz，图9（b）为内传动杆1阶弯曲振型，振动频率为433 Hz。

图9 传动杆组件典型低阶振型

试验测试的试车临界转速为26524 r/min；模态求解的仿真临界转速为25980 r/min，因此，仿真临界转速和试车临界转速的误差为

上述结果表明，本文提出的传动杆组件3维有限元建模分析方法具有很强的工程应用价值。按照所建模型求解得到的部件固有频率和传动杆临界转速的仿真值与试验结果相比均具有很好的一致性。

3 结论

（1）浮动花键连接的径向传动杆共振区间长，跨度可达3000～5000 r/min，进入共振后振动仍然持续快速增大，拉升转速避开共振不可行。

（2）传动杆弯曲位移响应先于轴承座加速度响应进入共振。前者增速慢、区间长；后者增速快、区间短。

（3）在试车时，如果在较小的转速区间内轴承座加速度振动增大了300%及以上，即可判定传动杆发生了横向弯曲共振。

（4）在试车临界转速下传动杆振动极易引发花键磨损等故障，必须避开或远离。

（5）综合考虑多部件结构、轴承支承刚度和花键连接刚度的3维有限元建模方法，不仅能够计算传动杆临界转速，也能预警轴承座共振。

（6）本文提出的临界转速判定方法应用于另外2台份传动杆的部件试验和整机试车的结果表明，试车临界转速和仿真临界转速的误差分别为2.5%和0.4%，具有一定的普遍适用性。