基于FPGA的磁轴承转子系统自适应振动抑制

肖 鹏，魏静波，胡宏锦，刘 昆，张志洲

（中山大学航空航天学院，广东 深圳 518107）

0 引言

磁轴承转子系统因其无机械接触、无需润滑、适应复杂工况以及主动可控等特点，已经在航空航天、机械加工、交通运输等诸多领域中广泛应用，同时也是航空发动机转子的一种重要支承方式。由于转子的加工误差、材料质量不均匀、运行后变形等原因，转子存在一定的不平衡量，在旋转中产生不平衡激振力而发生不平衡同频振动。此外，转子由高速电机驱动，在转动过程中，电机的电磁干扰将直接作用于电涡流传感器，进入控制回路后引起磁力的振动，进而引起转子的倍频振动。

针对转子不平衡振动，提出的主动控制方法从实现方式上主要分为2类：不平衡补偿法与自动平衡法。不平衡补偿通过电磁轴承产生相应电磁控制力补偿而抵消不平衡力的作用效果，从而强迫转子围绕其几何中心旋转。Taguchi等针对涡轮机的不平衡振动问题，提出了一种基于卡尔曼滤波器的前馈自适应不平衡控制算法；蒋科坚等通过系统对于试探性的补偿信号的动力学响应计算得到不平衡振动的Fourier系数，实现了不平衡补偿；Mao等提出了一种基于可变步长（Variable Step Size，VSS）多边迭代方法的不平衡系数搜索算法，并基于此算法产生相应的控制信号实现不平衡振动的补偿。由于VSS算法提取的是不随转速变化的不平衡质量的信息，所以计算成本较低，而且适合在转子转速变化的状态下进行不平衡补偿。

而自动平衡则是通过算法使得控制器对位移中的同频分量不响应，使转子绕惯性主轴转动。广义陷波和归一化最小均方（Least Mean Square，LMS）算法是其中最常用的2种方法。汤亮等提出了LMS算法的自适应数字陷波滤波器实现自动平衡的控制算法；高辉等着重分析了几类LMS算法在磁轴承转子系统中的应用，对原有算法进行了改进，实现了变步长的LMS算法；徐骏等利用LMS算法实现了单自由度悬浮试验台上的振动抑制，并分析了各种参数对振动控制性能的影响；Liu等设计了一种改进的双输入的自适应滤波器，通过调节收敛系数和补偿角度，能够在较宽的运行速度范围内自适应抑制同步电流，实现自动平衡。

针对电机干扰产生的传感器谐波扰动，张激扬等基于级联相移陷波器全转速自适应控制方法对磁轴承转子系统全转速范围内的传感器谐波扰动进行了主动抑制；王雨楠等提出一种变步长LMS算法实现了8倍频谐波振动的有效抑制；Peng等提出了一种多频谐振控制器（Multiple Resonant Controllers，MRC），采用渐进式调整和分段切换策略实现了系统全转速范围下的多频谐波扰动的抑制。

本文针对转子不平衡引起多种振动问题，提出了一种基于LMS算法的自适应滤波器。为了解决一般控制器算法计算延迟大的问题，构建了基于现场可编程门阵列（Filed Programmable Gate Array，FPGA）实时自适应振动补偿模块。

1 基于LMS算法的自适应滤波器

1.1 磁轴承转子系统振动源建模与分析

转子的不平衡量可以用附加质量的方法描述，扁平转子的结构如图1所示。电机转子安装在转子上半轴，电机定子安装在磁轴承与传感器之间，采用附加质量对转子不平衡量进行建模。转子的上、下平面中心分别为、，转子几何中心为；转子的上、下平面不平衡质量分别为、，2个不平衡质量距上、下平面几何中心的距离均为，转子转速为，上、下平面不平衡质量的相位差为。下、上轴承产生的指向、轴静不平衡力分别为f、f、f、f。

图1 扁平转子的结构

则4轴产生的静不平衡力分别为

作用于转子后产生的、轴振动位移信号应为

式中：A、A分别为、轴位移信号的幅值。

不平衡量是转子振动的1个重要来源。此外，在转动过程中，电机转子永磁体构成的磁场的转动会引起电涡流传感器的倍频扰动。根据试验可知，频率与电机转速同频之间存在倍数关系，这个倍数就是电机的极对数。电机的倍频干扰是1种加性噪声，直接与转子的真实位移量叠加，作为位移反馈进入控制回路，所以可以认为是1个位移信号，则倍频扰动信号的位移表达式为

式中：为扰动的幅值；为电机的极对数。根据电机设计的对称性，可以认为、轴的扰动幅值相等；而、轴传感器的安装位置相差90°，则、轴的扰动位移相位相差90°。同时，由于电机转子安装在转子的上半轴，距离上轴承传感器更近，与下轴承传感器相距较远，那么下轴承传感器的扰动幅值远远小于上轴承传感器的，可以忽略不计。

而当同时存在不平衡量以及倍频扰动时，转子的位移信号应在式（2）的基础上加入倍频扰动项，即

从式（4）中可见，无论是不平衡量引起的不平衡位移，还是电机磁场干扰带来的扰动位移，都以正弦信号的形式存在，并且作为位移信号进入传感器中。

倍频扰动在传感器环节引入，消除扰动信号使得控制器对于该信号不响应，就不会产生相应的电磁力，使转子稳定在平衡位置，此时倍频振动得以抑制。不平衡位移信号产生于转子的转动过程中，滤除不平衡位移信号，使控制器不对该信号产生控制力，从而令转子绕其惯性轴旋转，达到抑制不平衡振动的目的。因此，可以在反馈环节加入自适应滤波器，并且滤波器应该满足以下要求：能够自适应地进行频率跟踪；不破坏系统本身的稳定性；响应速度快；滤波效果好。

1.2 基于LMS算法的频率跟踪振动抑制

LMS算法通过不断调整滤波器的权值系数，使得滤波器的输出信号与参考信号之差的平方和（均方误差）最小，从而让系统输出所需信号的最佳估计，LMS算法基本原理如图2所示。

图2 LMS算法基本原理

其中，参考向量()作为算法的参考信号，

式中：为转子转速频率；输入信号（）为位移信号，其中为离散系统中的序号；输出信号为（），由参考向量中各分量线性叠加产生；滤波器权向量()=[]由LMS算法进行更新，式中分别为权向量的组成元素。误差信号（k T）是LMS算法的重要判断准则；而则为离散系统的采样时间。LMS算法基于最小均方误差的准则，均方误差为

其中（kT）可由输入信号与输出信号给出，

从式（7）可知，σ是1个关于的二次函数，对求导可得

式中：为参考信号（）的自相关矩阵；为输入信号（）与参考信号（）的互相关矢量。

为了求得最优解，从式（8）可知，必须求得的逆，这在实际应用中需耗费较多的计算资源，且计算时间长。此时，引入最陡下降法获取的递推公式，简化流程，取单个误差样本的梯度作为算法梯度，可以得到算法的递推方程组

式中：为算法步长，控制算法的收敛速度和稳态精度。

式中：为虚数单位。

将的递推式经变换得

联立式（10）、（11）、（12）可得以输出信号（）为输出，输入信号（）为输入的传递函数

式（13）零点为±e ，±e 。当输入信号频率与参考信号频率相等时，|G （）|=0。说明输入信号中的转速同频信号与倍频信号都能够被滤除。选取转速=3000 r/min，则此时转速频率=50 Hz，步长取值0.1、0.01、0.001，倍数=2，自适应带阻滤波器G（）的波特图如图3所示。

图3 自适应带阻滤波器G（fz）的波特图

从图中可见，G （）此时可视为1个带阻滤波器。从幅频响应可见，3种不同的步长值均能够滤除转速同频50 Hz与2倍频100 Hz的信号，证明了传递函数零点分析的正确性。并且滤波器对于位于之外的频率成分增益为1，为滤波的中心频率，为对应中心频率的阻带带宽，即中心频率两侧最近的幅值增益为-3 dB的2个点之间的带宽。与步长成正相关。当步长=0.1时，的值已经远大于2个中心频率之间带宽，导致自适应带阻滤波器对频率在50～100 Hz之间的信号也起滤除作用，与自适应滤波器只滤除定点频率的期望效果不符。而步长为0.001时，阻带带宽太小，当转子加速时，由于受算法收敛速度的限制，导致自适应滤波器达不到理想的滤波效果。

从传递函数的相频响应可见，自适应滤波器将会导致信号的相位畸变，并且步长越大，相位畸变越明显，产生相位畸变的带宽也就越大。当=0.001时，在第1个中心频率，虽然畸变的超前角和滞后角都比较大，但畸变带宽在2 Hz内，是1个比较小的尺度，因此对于信号整体相位的影响较小；而在第2个中心频率，相角从0～2π的过渡十分平滑，对信号相位基本没有影响。

加入自适应带阻滤波器后的控制系统如图4所示，、通道径向控制解耦，以轴的径向悬浮控制为研究对象。

图4 加入自适应带阻滤波器后的控制系统

图中（）为悬浮控制的控制器，一般采取PD控制器的形式；G （）为功率放大器的传递函数；（）为转子质心平动的动力学模型；，，分别为磁悬浮轴承的电流刚度系数、位移刚度系数、电涡流传感器的位移电压转换比。G （）即为自适应带阻滤波器的连续形式。以扰动位移（）为输入，转子平动位移（）为输出，写出控制系统的闭环传递函数

由式（13）可知

则有（）=0。此时，系统的输出（）=0。同理，将=带入式（14）得到（）=0。则在系统的位移输出中将不含有与转速同频和倍频的量，能够有效抑制转子的振动。再以扰动位移（）为输入，电磁轴承产生控制力（）为输出，得到该系统的控制系统的闭环传递函数

按照上述方法分析，在系统的控制力（）中也不包含含有与转速同频或倍频的量。因此，通过单频点的方法可以证明加入自适应带阻滤波器后的控制系统（图4）能够抑制转子的同频以及倍频振动。

1.3 模态频点振动抑制

当转子转速即将达到其模态频点时，不平衡振动将与磁轴承转子系统的模态振动相互影响，引起更大幅度的振动。

磁轴承转子系统的模态频点是1个或多个固定的频率值，可以通过仿真软件计算推导得出、或在激振试验和磁轴承转子系统的调试过程中大致估算出模态频率值。因频率值固定，可加入1个固定频率的自适应同频放大器与自适应带阻滤波器共同组成自适应滤波器。并且，当转子转速接近模态频率时，自适应滤波器应当自动切换到固定频率的滤波器。自适应同频放大器（）的传递函数为

取=3000 r/min，收敛系数=0.1，自适应同频放大器的波特图如图5所示，在频点50 Hz处，（）的增益为无穷大，并且起放大作用的带宽极小，而在放大带宽外其它频点处，（s）的增益基本都为0 dB。从相频响应看，其相角也能在畸变后很小的带宽内恢复为0。

图5 自适应同频放大器的波特图

自适应同频放大器（）的增益无穷大，不能单独作为滤波器使用，不过可以将其接入负反馈回路中，利用其同频信号开环放大倍数为无穷大，其余信号开环放大倍数为1，使得期望的同频信号的闭环增益为0，同时不影响其它信号的闭环特性。接入（）后的自适应滤波器控制系统如图6所示。

图6 接入N（s）后的自适应滤波器控制系统

选择不平衡静力（）为输入，转子平动位移（）为输出，得到控制系统的闭环传递函数

式中：（s）为牛顿第二定律的传递函数形式。

令=，带入式（19）中得到

则（）=0。系统的输出位移（）同样为0，即转速同频的信号已被完全滤除，抑制了同频振动，达到了最小位移控制的目的。

2 基于FPGA的自适应滤波器实现

2.1 SLMS算法

FPGA的特性决定了其能够在1个相当高的频率下稳定工作，而且拥有大量的乘加运算资源与存储资源，具有完全并行化的结构设计，与自适应滤波算法的需求完全契合。

为使LMS算法的计算更符合FPGA的运算规则，使计算速度进一步加快，引入符号类LMS算法（Signed Least Mean Square，SLMS）简化硬件复杂度。SLMS算法的主要思想是在权值更新环节引入量化误差函数，对参考信号（）和误差信号（）进行量化处理。而具体对哪一种信号进行量化，是SLMS算法类型的一种分类方法。仅对（）进行量化，称之为符号-数据LMS算法；仅处理（），是符号-误差LMS算法。由于在符号-数据LMS算法中对参考信号（）进行量化，使得算法权值更新的迭代方向与代价函数的最陡梯度下降方向不总是相同的，这导致在更新过程中平方误差频繁增大，从而出现不稳定问题。本文选用了更加稳定的符号-误差LMS算法对自适应滤波器进行实现。

首先对误差信号进行量化

式中：[]为量化计算函数，一般取符号sgn（）函数，即

步长可以取2的幂次方数，（）经过量化处理后只保留符号位，那么权值更新部分便不需要进行乘法运算，极大地简化了算法的硬件复杂度。同时，为改进SLMS算法的收敛性能，可以采取一种新的3级量化策略

当-＜（）＜，误差信号未达到阈值时，权值始终不更新，如果大于该阈值，权值更新方程为

从式（25）中可见，此时算法是一种时变步长的LMS算法，其收敛性能远超其他的符号类LMS算法的，同时具备结构简单、计算速度快的特点。

2.2 FPGA模块结构

自适应放大器是对固定频点进行滤波，只需要提前计算好滤波器权值系数即可，不需要对其权值实时更新，所以主要是对自适应LMS滤波器的结构进行设计。

自适应滤波器的顶层结构如图7所示。从图中可见，提取转子位移模拟信号（），通过模数转换器（Analog to Digital，ADC）转换为数字信号，并作为LMS滤波器的输入信号（）。通过转速解码模块对输入的转速信号进行解码获得此时的转速频率，经过直接数字频率合成（Direct Digital Synthesis，DDS）模块得到与转速相关的参考信号（）。模块输出则为滤波后的信号（）。若ADC的采样频率与控制器的控制频率不相同，则还需要进行时间同步的处理。

图7 自适应滤波器的FPGA顶层结构

LMS滤波器计算单元的结构如图8所示。

图8 LMS滤波器计算单元结构

图中

只展示了LMS滤波器的同频滤波模块，以同频的正弦及余弦信号为参考信号。而事实上，同频滤波模块与倍频滤波具有复用性，只需要输入倍频的参考信号即可进行倍频的滤波。LMS滤波器还具有可叠加性，将输出（）与同频信号滤波器的输出相加后进入权值更新的环节，就相当于2个滤波器在结构上相串联，但由于FPGA的并行计算特性，只会多出1个加法的计算时间，而不像DSP、Arm等嵌入式控制器，是2个滤波器计算时间之和。并且，当扰动信号为多个倍频信号叠加，相应地串联多个对应频率的滤波器即可。此外，考虑到FPGA的计算特性，滤波器还采用了参考信号循环移位的方法构建高阶滤波器，利用参考信号前后时刻间的关联性使得每个基本单元具有相互补偿作用，可以达到更好的滤波效果。即使参考信号输入不完整，即参考信号只有正弦或只有余弦部分，也能够达到滤波的效果。在同时采用定点数进行计算、主频皆为150 MHz、均实现16阶LMS滤波器的条件下，各类硬件平台的型号及运算时间见表1。

表1 不同硬件平台算法架构、型号及其运行时间

从表中可见，FPGA的运行速度约为DSP 28335平台的25倍，约为ARM STM32F103平台的81倍。由于FPGA的并行架构，滤波器的权值计算处于并行状态，相当于16阶的权值计算与1阶的权值计算时间相等。相应地，ARM以及DSP均为串行计算，16阶权值计算时间是1阶权值计算时间的16倍。此外，FPGA以及DSP均能调用硬件乘法器，定点运算只需要1个时钟周期即可完成，所以二者运算速度均远超ARM的。同时，DSP在运算时需要消耗额外的时间来等待指令、存取数据。

3 仿真结果及分析

3.1 自适应频率跟踪振动抑制

自适应频率跟踪振动抑制仿真所用参数有：转子质量=4.8 kg；位移刚度系数k=50000 N/m；电流刚度系数=125 N/A；传感器位移-电压转换系数=8000 V/m；功放环节增益=0.00004 A/V；功放环节时间常数=0.0005，转速=2000 r/min。对同频及2倍频位移成分抑制的仿真结果如图9所示。仿真开始时转子处于悬浮状态，第2 s时启动自适应滤波器。

图9 对同频及2倍频位移成分抑制的仿真结果

从图中可见，在第0～2 s时，由于自适应滤波器未开启，在不平衡位移与倍频扰动位移的共同作用下，转子在轴上振动，并且位移信号的形式是转速同频与2倍频信号叠加。启用自适应滤波器后，转子的位移迅速收敛，并在第4 s时基本收敛到0，证明了自适应滤波器对于转速同频及2倍频位移信号能够起到很好的抑制作用。

磁力响应的曲线如图10所示。与位移响应类似，在第0～2 s时，控制器对转速同频与2倍频信号叠加的位移信号响应，并输出相应控制磁力，自适应滤波器开启后，控制器对于位移信号的转速同频和2倍频成分不响应，此时磁力曲线迅速收敛。证明了自适应滤波器对于磁力的振动能起到抑制的作用。

图10 磁力响应曲线

在转子以恒定加速度加速的过程中（加速度为5πrad/s），加入自适应滤波器后的位移响应如图11所示。

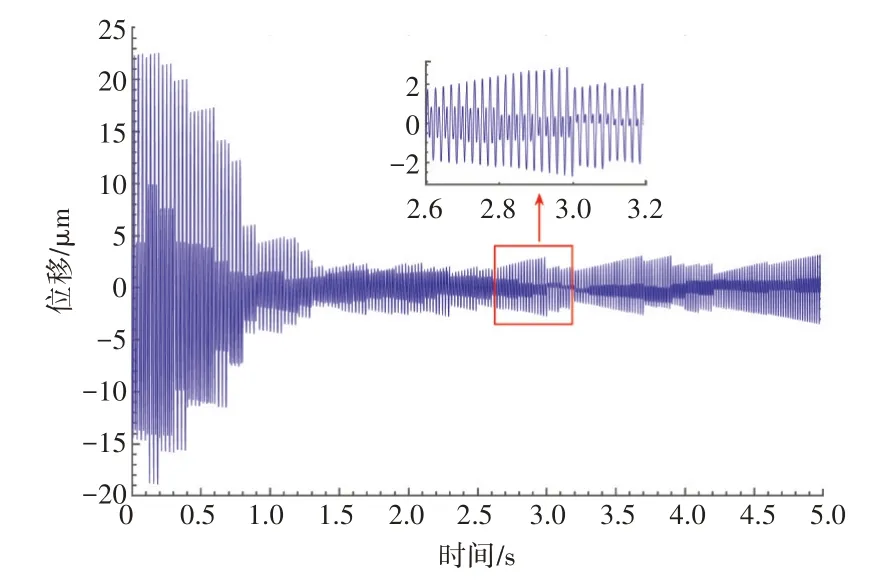
图11 加速过程位移响应曲线

从图中可见，位移响应分2个阶段：在第0～1 s时，处于收敛过程，滤波器的权值跟随扰动频率在持续变化，在自适应滤波器的作用下迅速收敛到1个较小值，约为原幅值的1/10；在第1 s以后，转速在持续变化，参考信号的不断变化使得权值在短时间内难以快速收敛，不能终止于维纳解，即最优解，导致抑制效果差于定频率的效果。

3.2 模态频点振动抑制

模态频点振动抑制仿真参数与频率跟踪参数相同。转速达到模态频点时，不平衡力是1个幅度为50 N的正弦信号形式。若不对这个力进行控制、补偿，位移信号将会逐渐发散。

在反馈回路加入自适应同频放大器后模态频点的位移响应曲线如图12所示。从图中可见，转速同频的位移响应在1 s内迅速收敛到0附近。说明自适应滤波器对模态频点的位移振动能起到完全抑制的作用。

图12 模态频点位移响应曲线

4 自适应振动抑制试验

为验证基于FPGA的SLMS算法自适应滤波器对特定频率成分的抑制效果，进行自适应振动抑制试验。试验相关参数包括：FPGA时钟频率为10 MHz，ADC采样频率为50 kHz，输入信号由1、5 kHz 2个频率的正弦信号构成，幅度比值为1∶1，均为1.5 V，试验目的为滤除1 kHz的正弦波干扰，而不破坏5 kHz的正弦波，从而检验算法的有效性。

输入信号电压随时间变化关系如图13所示。进入自适应滤波器后的误差信号即所求信号，对其做傅里叶变换，其频谱如图14所示。

图13 输入信号电压时间关系

图14 误差信号频谱

从图中可见，1 kHz频率幅值减小了将近80%，而5 kHz频率成分幅值没有明显变化，说明基于FPGA的自适应滤波器能够完成滤除特定频点的任务，且对于其阻带带宽外的频率成分不会产生抑制作用。但由于受FPGA有效字长效应的影响以及ADC精度的限制，不能达到将特定频率成分信号完全滤除的效果。

5 结论

（1）数值仿真表明，所设计的基于LMS算法的自适应滤波器对恒定转速下的转子同频与倍频振动以及模态振动能够完全抑制，对加速状态下的转子振动能够抑制90%左右。

（2）基于FPGA设计的SLMS算法自适应滤波器的模块结构经试验验证对特定频率成分的抑制效果达到80%以上。