新型跟踪微分器在航空发动机磁悬浮轴承中的应用

张和洪，谢晏清，王 娟，但志宏，林泽如，龙志强

（1.福州大学计算机与大数据学院，福州 350108；2.大连海事大学轮机工程学院，辽宁大连 116026；3.中国航发四川燃气涡轮研究院，四川 绵阳 621703；4.福建省民益建设工程有限公司，福州 350018；5.国防科技大学智能科学学院，长沙 410073）

0 引言

磁悬浮是借助磁力来克服重力的一种涉及多学科领域的复杂技术，已应用于航空航天、医学、能源工业、轨道交通等重要领域。航空发动机磁悬浮轴承技术中最核心的环节是将运动中的转子稳定悬浮于空中，使转子和静子之间不存在机械接触，从而大幅提升航空发动机性能。因此实现稳定悬浮是磁悬浮轴承应用的核心技术之一。

Smirnov等指出磁悬浮轴承是包含非最小相位系统的具备强非线性和大量不确定性的系统。在磁悬浮轴承控制问题上，Matsumura等总结了国内外学者在基于数学模型或弱基于数学模型的研究探索与试验验证；Giap等提出模糊比例、积分、微分（Proportional Integral Derivative，PID）控制及滑模控制；Wu等提出反步控制；Sun等提出自抗扰控制及迭代学习控制等。为实现稳定悬浮，金超武等指出控制器需要获取位移传感器实时的信号及速度信号。但由于航空发动机工作温度高且负荷变化大，使位移传感器信号包含较大的随机噪声，且信号频带会随工况改变，增加了控制器设计的难度。如何设计高效的微分器算法应用于位移传感器，实现实时有效的滤波与速度信号提取，特别是提高信号的相位品质，成为实现稳定悬浮的关键问题。理想微分器在物理上不可实现，Zhang总结了国内外研究人员在微分器理论与应用研究方面的成果，目前国内外主流微分器算法包括以色列学者Levant及Utkin提出的滑模微分器算法与中国学者韩京清提出的跟踪微分器算法。滑模微分器中由于切换函数的存在，不能保证系统变量在有限时间内到达滑模面并保持在滑模面上，而是在滑模面附近快速切换，产生抖振现象。考虑到快速性，韩京清从最小时间问题出发，引进了快速跟踪微分器算法，具有无超调、无颤振的特点，能获取品质良好的微分信号。然而该微分器的抗噪声能力仍受到一定程度的限制，若输入信号的信噪比较小，会产生较大的毛刺甚至产生淹没现象，若提高算法滤波因子，则在改善信号光滑性的同时，产生较大的滞后。因而跟踪微分器存在光滑性与相位滞后之间的矛盾。

由于跟踪微分器具备全程快速、无颤振等优势，本文为弥补算法在滤波与微分信号提取时的相位滞后，引入相位调整因子对相位进行实时有效地补偿，在光滑性与相位滞后之间作适当权衡，采用基于2阶串联型系统的跟踪微分器解决位移传感器信号处理问题。

1 问题提出

磁悬浮轴承是一个复杂的机电耦合系统，其性能优劣很大程度上取决于核心反馈控制器的性能。磁悬浮轴承悬浮控制系统的原理如图1所示。

假定在参考点上，当外界存在向上或向下的扰动作用于转子时，转子位置会偏离参考点。此时安装在电磁铁上的位移传感器将实时检测出转子偏离参考点的位移以及相应的状态量，并作为反馈控制器的输入，通过相应的斩波电路等功率放大器将控制器的输出转化成控制电流，进而在悬浮电磁铁中产生相应的磁力，最终驱动转子返回平衡位置。在磁悬浮轴承工程实践中，位移（即间隙）及对应的速度信号对于实现稳定的悬浮至关重要。在通常情况下，速度信号可通过加速度计的积分获得，但是在实际工程应用中，加速度计存在2个主要问题：（1）价格较贵的加速度计相比于位移传感器而言，安装工况恶劣，容易发生故障；（2）加速度计信号的积分对某些特殊的信号频带无法实现有效提取，特别是当处于稳定静态悬浮时，信号中存在直流分量，在利用积分方法获取速度信号时被放大。此外，在磁悬浮轴承工程应用中，位移信号存在较大的随机噪声干扰，且随着系统运行工况的改变，位移信号的频带宽度会发生变化。因此为实现航空发动机磁悬浮轴承的稳定悬浮，亟需设计有效的跟踪微分器算法（如图1所示），通过直接处理位移传感器采集信号获取有效的滤波与速度信号，用于磁悬浮轴承的悬浮控制。有效的跟踪滤波与微分信号主要表现在2方面：（1）跟踪滤波和微分信号的跟踪误差满足实际系统的要求；（2）与给定信号相比，跟踪滤波与微分信号的相位滞后尽可能小。

图1 磁悬浮轴承悬浮控制系统原理

2 新型跟踪微分器算法构造

考虑2阶积分器串联型系统有

式中：=[,]，表示系统（1）的2个状态，系统的初始状态为(0)=[(0),(0)]；为控制量的极值约束条件参数；为根据时间最优控制理论得到的式（1）系统以原点为终点的时间最优控制综合函数

为bang-bang控制的开关曲线方程，bang-bang控制是一种控制量在最大值和最小值之间切换的控制方式，在开关曲线的上方=-，开关曲线的下方=+，这样选取的控制量可使给定初始状态回到开关曲线上，且在开关曲线上至多跳变1次便可回到原点。开关曲线及状态转移最优轨迹线如图2所示。

图2 开关曲线及状态转移最优轨迹线

图中

即为开关曲线。从图中可见，初始状态的选择不会影响系统状态转移的最终目的，初始状态必然会转移到开关曲线上，而后顺着开关曲线快速回到原点。把式（3）中的改为-()（()为给定的输入信号），得到最速跟踪微分器

为了消除离散化后的最速跟踪微分器在稳态时出现的高频颤振，韩京清利用等时区方法推导出状态变量在开关曲线附近来回跳变的线性区域以及该区域所对应的边界层函数。边界层的存在使得状态在转移过程中能够无颤振回到指定点。对应的控制量在有界区域内按线性规律变化，而不是在2个极端的量（最大值和最小值）之间跳变，有利于克服由式（6）系统引发的高频颤振现象。

采用欧拉折线法将式（1）系统离散化后，可得控制量受限的2阶离散系统

式（7）离散系统到达原点的快速最优控制综合函数的确定方法为：先确定用控制序列（0），（1），…，（）能到达原点的初始点(0)的表达式，然后设法用初始点(0)来表示出初始时刻的控制量(0)，那么这个控制量(0)就是初始点(0)的最优控制量，这个(0)的表达式就是最优控制综合函数。详细推导过程见文献[18]。为便于理解，本文给出重要研究结论，对应的边界层方程为

式中：、、分别为边界层A、B、C对应的曲线方程。

边界层内部的2步可达区为

式中：（2）为2步可达区，一旦状态落入该区域，在2步控制作用下将回到原点。

2步可达区及线性边界如图3所示。

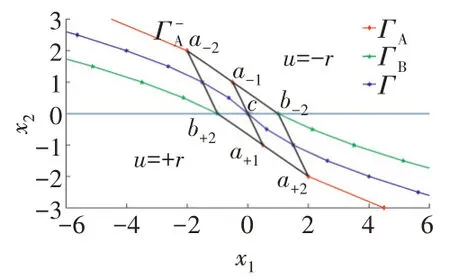
图3 2步可达区及线性边界

式中：为滤波因子。

用()-()代替式（7）中的()，得到基于离散时间最优控制算法的跟踪微分器算法

通过大量仿真分析发现，采用最优控制综合函数式（12）构造的跟踪微分器算法式（13）在输入信号的噪声强度变化时，式（13）系统得到的滤波与微分信号存在较大的相位滞后问题。为此，做出合理假设，认为跟踪信号与微分信号仅仅产生了时间上的滞后，而幅值没有变化，那么根据一元函数微分学可以得到1组近似的数学关系。假设输入信号()经过跟踪微分器算法后获得了跟踪信号(-Δ)以及微分信号(-Δ)，考虑到时间最优控制问题得到的加速度，从而有近似的一元微分关系

研究发现，当选择1个恰当的数值Δ=·T ·时，可以改善相位与光滑性的矛盾，从而改进了韩氏跟踪微分器，得到1个合适的微分信号。T 为离散采样周期，为调整系数，根据具体的信号可以取1个适当值，从而在一定的范围内获得比较好的滤波与微分信号。最终得到的算法为

3 仿真及试验测试

从时间域（即时域）和频率域2个维度分析所设计的新型跟踪微分器算法式（15）在给定信号下的跟踪滤波与微分提取的性能，同时对磁悬浮轴承悬浮控制系统中位移传感器所获取的实时数据进行处理，分析其滤波与微分提取能力。

3.1 时域分析

所有仿真的系统状态的初值都选择为=(1),=0，系统采样时间步长=0.001 s，系统的给定输入信号为()=((),)，其中()为给定的基信号，函数用于添加相应强度高斯白噪声，为随机噪声的强度。在航空发动机磁悬浮轴承中位移传感器的噪声强度为45～60 dB。当输入信 号 为()=(sin(4π),50)或 为()=(sin(2π)+cos(2π),45）时，从时域的角度对比基于的跟踪微分器算法与本文所提出的改进新型跟踪微分器算法在不同给定输入信号下的跟踪滤波与微分提取性能。

当输入信号为()=(sin(4π),50)时，2种算法的快速因子=1000，滤波因子=25，对于改进的新型跟踪微分器算法的相位调整因子=37.5。跟踪滤波与微分信号提取效果对比如图4所示。

图4 当输入信号为vn(t)=awgn(sin(4πt),50)时，跟踪滤波和微分信号提取效果对比

当输入信号为（）=（sin（2π）+cos（2π）,45)时，2种算法的=1000，=50，=75。跟踪滤波与微分信号提取对比效果如图5所示。

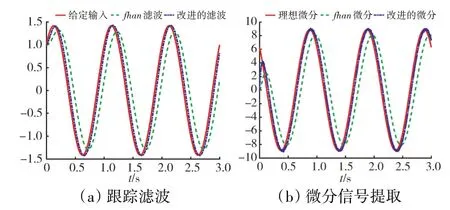
图5 当输入信号为vn(t)=awgn(sin( 2πt)+cos(2πt),45)时，跟踪滤波与微分信号提取效果对比

通过以上对比分析可知，针对给定的输入信号2种算法都能够给出相应的跟踪滤波与微分信号。与基于的跟踪微分器算法相比，本文提出的新型跟踪微分器算法具备跟踪更快速的动态特性，且相位滞后现象得到有效改善，相位滞后约减小80个采样周期。

3.2 频域分析

采用扫频测试的方法绘制基于本文所设计的新型跟踪微分器式（15）的Bode图，利用Bode图分析跟踪微分器的频域特性。频域分析的目的是为了测试在理想状态下跟踪微分器的频域特性，故这里输入的正弦信号不掺杂随机噪声。因此，在仿真过程中取=1，考察选取不同快速因子对所设计的跟踪微分器频域特性的影响。其中=100、250、500、750，=0.001s。输入信号为正弦信号()=sin(2π)，频率的起始频率为0.1 Hz，终止频率为10 Hz，时间步长为0.5 Hz。对每个频率点，运行20000个采样时间，并记录采样区间[10000,15000]的数据。所设计的新型跟踪微分器滤波和微分的幅频和相频曲线仿真测试结果如图6所示。

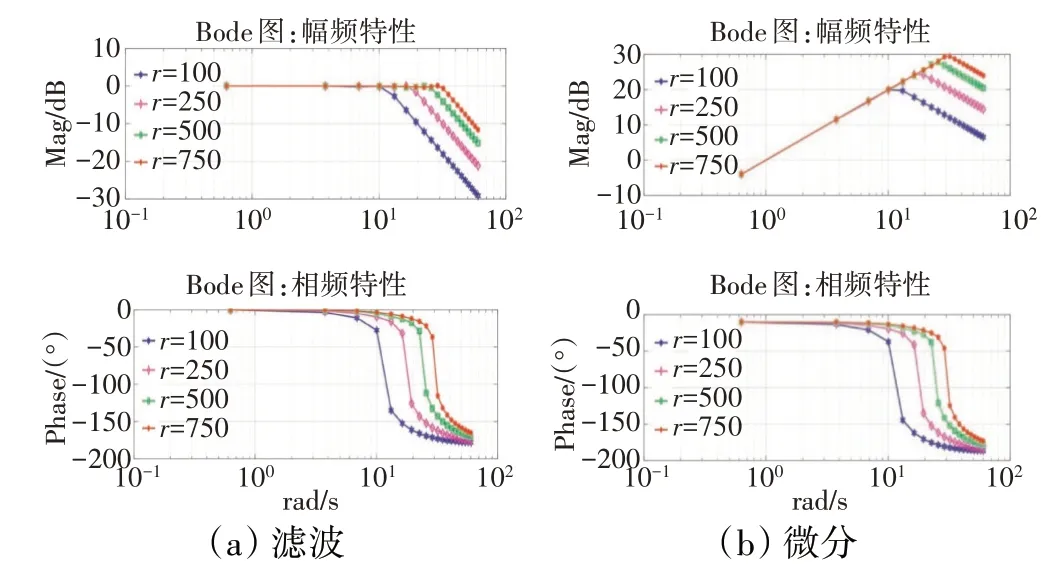
图6 在正弦输入信号条件下新型跟踪微分器滤波和微分的幅频和相频曲线

从图6（a）中可见，所设计的新型跟踪微分器的滤波幅频特性由2条直线形成折线，当频率低于转折频率时，幅频特性是1条平行于横轴的直线，纵坐标为0，即幅值没有发生变化；当频率高于转折频率时，频域特性是1条在转折频率处穿越横轴的直线，其斜率为-40 dB decade，即幅值呈现衰减态势，而该跟踪微分器的滤波相频特性有如下特点：在转折频率之前随着频率的提高，相移变化缓慢；但在转折频率附近，相移突然增大，穿过-90°而接近-180°；对于不同的速度因子，其幅频特性和相频特性呈现完全一致的变化规律，只是对转折频率做了相应的平移，速度因子越大，则带宽越大，即速度越快。分析图6（a）可知，所设计的新型跟踪微分器的滤波频域特性的最大特点是其通带内有较小的相移，而且不产生谐振，此外，该跟踪微分器的高频增益会随着频率的提高而减小，即有明显的高频噪声抑制能力。因此，本文所提出的新型跟踪微分器在通带范围内可以保证过渡时间较短、不出现超调、对信号进行实时滤波。

从图6（b）中可见，当频率低于转折频率时，幅频特性是1条不衰减的直线，其斜率为20 dB decade；当频率高于转折频率时，幅频特性是1条衰减的直线。而该跟踪微分器的相频特性表现为：在截止频率之前几乎保持超前90°相角，当频率接近转折频率时相移突然增大，穿过0°并很快接近-90°，此后一直保持在-90°附近。的变化对微分频域特性的影响为：对于不同，其幅频特性和相频特性呈现完全一致的变化规律，只是对转折频率做了相应的平移，越大，则带宽越大，即速度越快。上述分析结果表明，在通带内，所设计的新型跟踪微分器具有品质很好的微分特性，不仅能够获取微分信号，还可以滤除高频噪声，具有很好的工程应用价值。

所设计的新型跟踪微分器的频域分析结果表明，在通带范围内该跟踪微分器的滤波特性类似于2阶线性低通滤波器，且具有线性系统无法比拟的优点，即在通带内有较小相移的同时不产生谐振现象，因此，跟踪微分器是解决线性系统中超调与快速性之间矛盾的一种途径。此外，所设计的新型跟踪微分器的微分特性在通带范围内类似于纯微分器，而优于纯微分器的是该跟踪微分器对高频噪声不敏感，且可以物理实现。

3.3 试验数据分析

在磁悬浮轴承悬浮控制系统中，间隙信号滤波与速度信号获取对实现磁悬浮轴承的稳定悬浮控制至关重要。针对电涡流位移传感器采集信号，通过对比基于的跟踪微分器算法与本文所设计的新型跟踪微分器算法的处理效果，验证本文所设计算法的有效性与优势。

在如图1所示的磁悬浮轴承悬浮控制系统中位移传感器的采样频率为1000 Hz，系统稳定的悬浮间隙为8 mm，在试验过程中允许稳定误差为±0.5 mm。在测试过程中以磁悬浮轴承起浮阶段为系统运行工况采集位移传感器数据。系统状态的初值都选择为=(1),=0，=0.001s。2种算法的=3000，=15；改进后的新型跟踪微分器算法的=20。位移传感器信号跟踪滤波和微分信号提取效果对比如图7所示。

图7 位移传感器信号跟踪滤波和微分信号提取效果对比

从图中可见，磁悬浮轴承的悬浮间隙从12 mm起浮上升至稳定悬浮所对应的8 mm。对比基于的跟踪微分器算法，本文所设计的新型跟踪微分器算法能够有效获取滤波后的间隙信号与速度信号，且相位滞后现象得到有效抑制。

4 结论

（1）所提出的新型跟踪微分器算法能够快速获取给定信号的跟踪滤波与微分信号；

（2）相比于现有跟踪微分器算法，新算法所获取的信号在相位表现方面得到大幅度提升，平均相位滞后减小80～100个采样周期；

（3）新算法为磁悬浮轴承传感器信号处理问题提供了一种有效的方法和新思路，为研制航空发动机磁悬浮轴承技术提供了良好的技术保障。

接下来的工作包括但不限于：分析新型跟踪微分器算法的收敛性，为实际工程应用提供理论保证；分析新型跟踪微分器算法在跟踪滤波与微分信号提取方面的精度，为进一步改进算法提供新的思路；基于所引入的相位调整因子，设计相应的自适应率，使得所设计的算法能够随着传感器信号的改变而自动调整相关参数，或者对给定信号通过插值或拟合等平滑处理后进行微分信号提取，以期满足实际系统对信号处理在光滑度和相位等方面的性能需求。