机动飞行下机载磁悬浮转子振动响应

张 越，周 瑾，金超武，张一博，周 扬

（南京航空航天大学机电学院，南京 210016）

0 引言

为了使航空器在未来满足更快、更经济、更可靠、更环保的使用需求，航空发动机正朝着高推重比、低油耗、经济可承受等方向变革与发展。磁悬浮轴承具有无摩擦、无润滑、寿命长等特点，将磁悬浮轴承应用于航空发动机，其优势包括：（1）减轻发动机质量；（2）提高发动机效率；（3）提升发动机安全性；（4）提升轴承工作温度和DN（轴承内径×轴的转速）值；（5）可主动控制及在线监测；（6）降低运营成本。

自20世纪80年代起，美、欧相继推出各类研发计划，旨在探究磁悬浮轴承在航空发动机上应用的可能性。1988年，美国制定了为期15年的高性能涡轮发动机综合技术（Integrated High Performance Turbine Technology，IHPTET）计划，其中1项主要内容是研究采用磁悬浮轴承支承的多电发动机，并完成了对内置式起动机/发电机、高温径向磁悬浮轴承、轴承保护的技术验证工作。1998年，英、法、德等欧共体5国共同制定了航空发动机用主动磁悬浮轴承（Active Magnetic Bearings in Aircraft Turbo-machinery，AMBIT）计划，专门研究用以支承多电发动机的高温磁悬浮轴承，并计划将其率先应用于民用航空发动机上。作为IHPTET的后续研究计划，美国国防部等部门于2003年共同发起了通用经济可承受先进涡轮发动机（Versatile Affordable Advanced Turbine Engine，VAATE）计划，考虑到磁悬浮轴承可为航空发动机状态监测、振动控制以及整体起动发电机等问题提供有效的解决方案，因此对于磁悬浮轴承的研究是VAATE计划的重要组成部分，并在智能发动机领域开展磁悬浮轴承的技术验证工作。

飞机机动飞行会改变作用在航空发动机上的载荷，进而影响磁悬浮轴承转子系统的性能，为了使磁悬浮轴承在发动机上得到应用，需要研究机动飞行对机载磁悬浮转子的影响。祝长生对航空发动机磁悬浮转子系统的动力学特性进行了试验研究，发现磁悬浮转子系统的振幅随基础振动幅度的增大而迅速增大；Xu等和姜豪等分别探究了磁悬浮刚性转子在基础正弦、冲击激励和基础倾斜工况下的振动响应规律；Jarroux等探究了强基础激励下磁悬浮转子的稳定性和动力学特性；Soni等提出了一种4元素控制方法，有效抑制了由基础运动引起的磁悬浮转子振动；黄春新以悬挂在机翼上的磁悬浮Jeffcott转子为对象，研究了飞机基本飞行动作下转子的振动特性；张鹏等分析了俯仰角速度、滚转角速度等机动参数对磁悬浮刚性转子稳定性的影响。

本文利用3个参考坐标系来表征大地、飞机、磁悬浮转子之间的关系，建立了机动飞行下磁悬浮柔性转子模型，通过对1个单盘转子进行数值仿真分析，探究了机动飞行对磁悬浮转子振动响应的影响。

1 转子建模假设与参考坐标系

为了便于机动飞行下机载磁悬浮转子建模，在不影响分析结果的前提下，作如下假设：

（1）磁悬浮轴承支承的转子与飞机机身轴线同轴，转子位于飞机的质心处，飞机的机动飞行即为磁悬浮转子的基础运动；

（2）转子简化为1个单盘柔性转子，由刚性圆盘、弹性轴段、不平衡质量组成，不平衡质量分布于刚性圆盘上，不考虑转子的轴向运动和扭振；

（3）转子的转速为定值，不考虑转子变转速带来的影响。

为了建立磁悬浮柔性转子的运动微分方程，需要得到转子相对于大地的运动，可以建立3个参考坐标系进行分析，基础运动下磁悬浮轴承转子如图1所示。

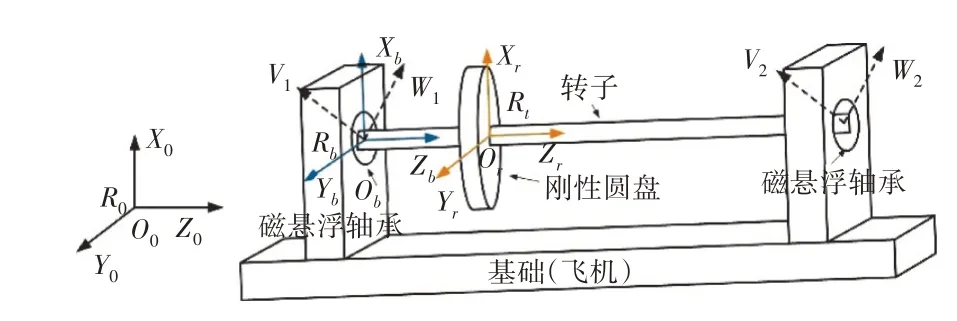
图1 基础运动下磁悬浮轴承转子

3个坐标系分别为：

（1）固连于大地的惯性坐标系（--），原点为；

（2）固连于飞机的非惯性坐标系（--），其原点为左磁悬浮轴承的中心，该坐标系随着飞机运动，用于描述飞机相对于大地的运动，如图2所示；

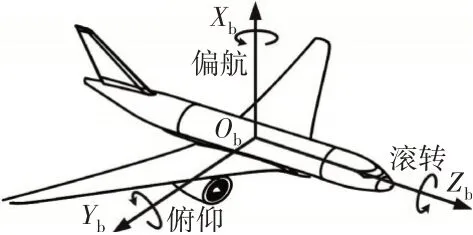
图2 飞机坐标系

（3）固连于转子的非惯性坐标系（--），原点为圆盘的几何中心，随着转子旋转，用于描述转子相对于基础的运动。

把飞机视作刚体，其在空中的平动机动飞行可以用、、描述，即坐标系相对于的平动即为原点相对于的平动。飞机在空中的转动机动飞行可以用、、描述，坐标系相对于的转动可以看作依次绕、、轴旋转、、，则相对于的瞬时角速度为

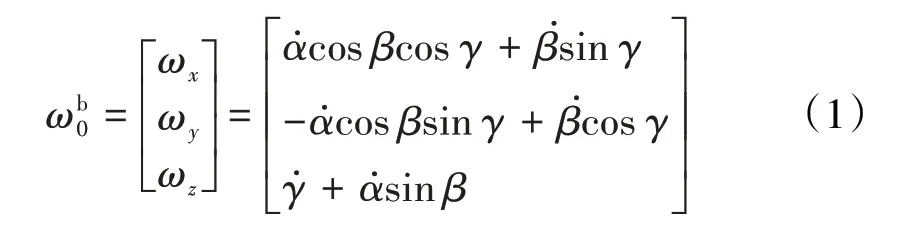
同理，坐标系可以看作通过依次绕、、轴旋转、、得到，相对于的瞬时角速度为

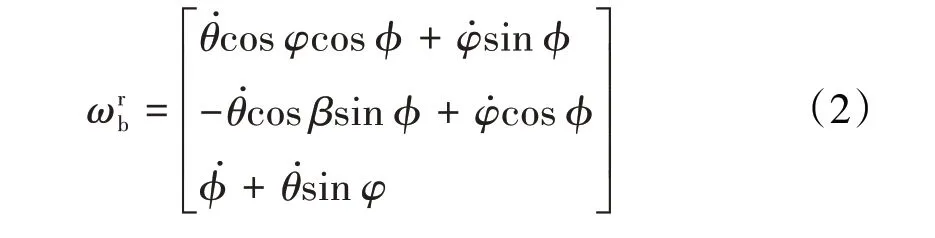
2 机载磁悬浮柔性转子系统动力学模型

2.1 机载柔性转子运动微分方程

通过坐标系的变换可以得到转子上任一点的绝对速度与绝对角速度。弹性轴段采用铁木辛柯梁单元进行建模，刚性圆盘视为集中质量，不考虑势能。分别计算刚性圆盘、弹性轴段单元和不平衡质量的动能和势能，运动微分方程可以由拉格朗日方程得到

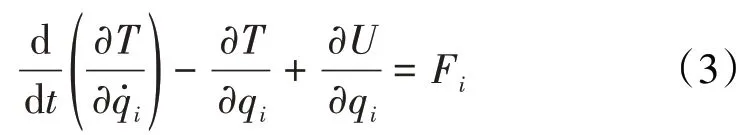
式中：q为有限单元的广义坐标；和分别为单元的动能和势能；F为单元受到的广义力。

通过对所有单元的运动微分方程进行合并组装，转子的运动微分方程为

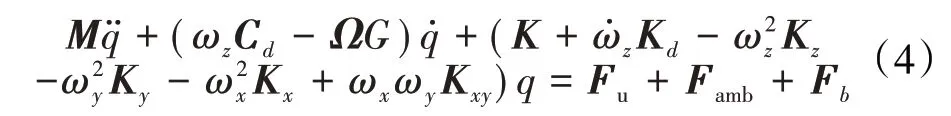
式中：为转子的广义坐标；、和分别为转子的质量矩阵、结构刚度矩阵和陀螺矩阵；为与基础转动ω有关的附加阻尼矩阵；、K 、K 、K 、K 分别为与基础转动ω、ω、ω有关的附加刚度矩阵；为转子受到的不平衡力矩阵；为磁悬浮轴承支承力；为飞机机动飞行运动引起的外力矩阵，其与机动飞行的6个参数都有关。

由式（4）可知，机动飞行运动会对转子系统产生附加刚度和附加阻尼，并施加外力扰动，影响转子的稳定性和振动响应。

2.2 磁悬浮轴承模型

磁悬浮轴承利用可控电磁力支承转子，其系统基本工作原理如图3所示。从图中可见，位移传感器实时检测转子位移并与参考位置作差，控制器对误差信号进行处理，产生控制电压，再经过功率放大器产生控制电流，驱动线圈产生相应的电磁力，通过不断调节，使转子悬浮于指定的参考位置。

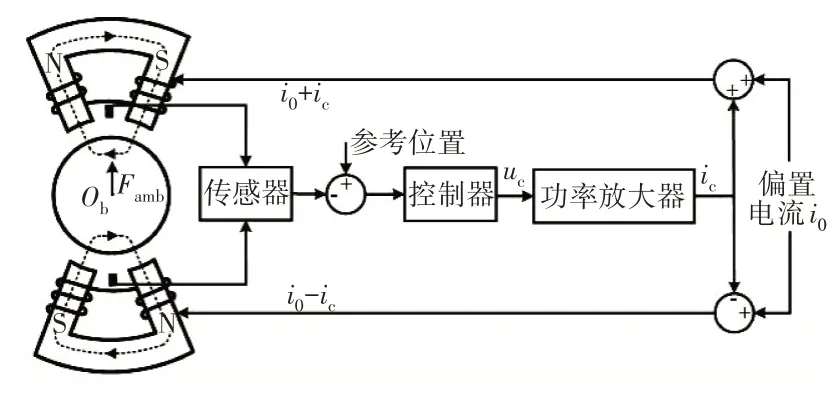
图3 磁悬浮轴承系统工作原理

本文采用8极C型磁极磁悬浮轴承，如图4所示。2对磁极分别产生、2个方向的电磁力，、分别与、方向有45°夹角。同一对磁极上的线圈采用偏置电流叠加控制电流的差动驱动方式。以方向为例，当转子偏离轴承中心时，产生的电磁轴承力为

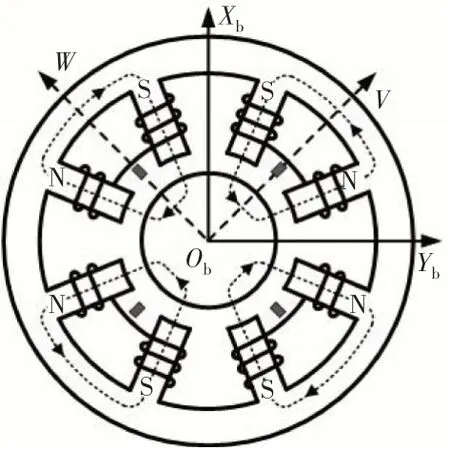
图4 8极C型磁极磁悬浮轴承结构

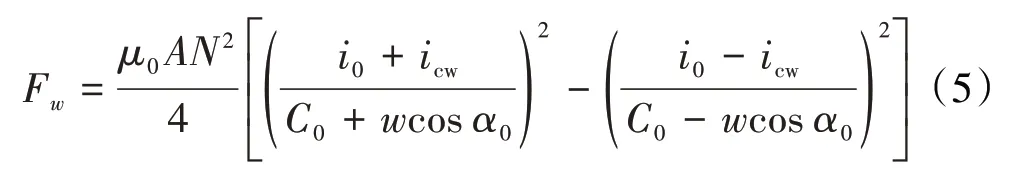
式中：为真空磁导率；为单个磁极面积；为1对磁极上的线圈总匝数；为转子位于轴承中心时的单边气隙；为线圈偏置电流；为线圈控制电流；为1对磁极夹角的一半。

在转子参考位置处对式（5）进行泰勒展开，略去高阶小量后得到电磁力的线性化公式

当磁悬浮轴承使用比例-微分（Proportional Derivative，PD）控制器时，功率放大器和位移传感器视为增益，i 为

式中：为控制器比例系数；为控制器微分系数；为功率放大器增益；为位移传感器增益。

把式（7）带入式（6）得

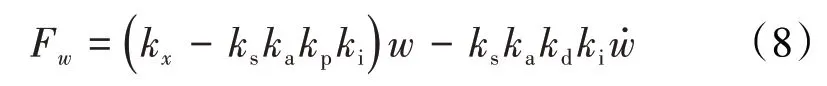
从式（8）中可见，使用PD控制的磁悬浮轴承可以为转子提供支承刚度和阻尼。同理可得磁悬浮轴承在方向产生的电磁轴承力F，则磁悬浮轴承在、方向的轴承力为

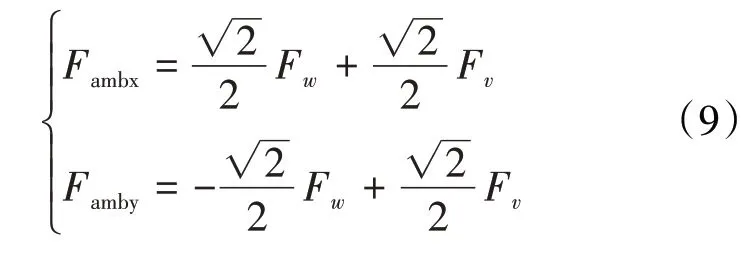
3 飞机机动飞行过程

飞机的机动飞行可以分为水平面内、垂直面内和3维空间的运动。水平面内的机动飞行包括转弯、盘旋等；垂直面内的机动飞行包括俯冲、拉升等；3维空间内的机动飞行为前2种运动的复合运动形式，常见的有横滚、筋斗、战斗转弯等。本文选取飞机在水平面的转弯和垂直面的俯冲拉升2种典型的机动飞行进行分析。

3.1 转弯机动飞行

飞机的转弯机动飞行过程是偏航、滚转、匀速前进运动的结合。以向右转弯为例（如图5所示），由于是水平机动，飞机俯仰角为=0。转弯可简化为5个阶段：（1）飞机正常直线平飞巡航；（2）开始转弯，机身沿轴线向右滚转至预定角度，同时开始向右偏航；（3）飞机保持固定滚转角与偏航角速度右转弯；（4）开始退出转弯状态，机身反方向滚转至角度为0，同时偏航角速度逐渐降至0；（5）飞机回到直线平飞状态。

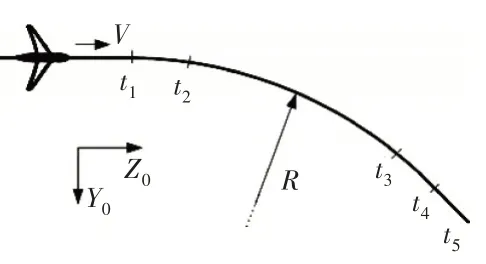
图5 飞机右转弯机动飞行过程

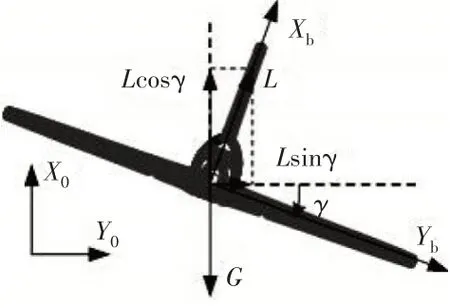
图6 飞机转弯过程受力

在转弯过程中，飞机保持恒定的平飞速度，盘旋半径为，在转弯阶段（3）时，飞机受力如图6所示，飞机升力与重力之间的关系为

3.2 俯冲拉升机动飞行

飞机在做俯冲拉升运动时不产生偏航或滚转，即=0、=0，如图7所示。俯冲拉升运动可以分为7个阶段：（1）飞机正常直线平飞巡航；（2）向下加速俯冲，俯仰角速度为负；（3）继续向下俯冲，但速度放缓，俯仰角速度为正；（4）飞机保持固定俯仰角速度俯冲，经过最低点后开始拉升；（5）飞机拉升，俯仰角速度为正；（6）继续拉升，俯仰角速度为负；（7）飞机结束俯冲拉升运动，回到水平直线飞行状态。

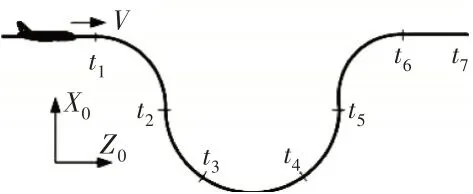
图7 飞机俯冲拉升机动飞行过程

飞机拉升过程受力如图8所示，飞机俯冲拉升飞行运动参数为

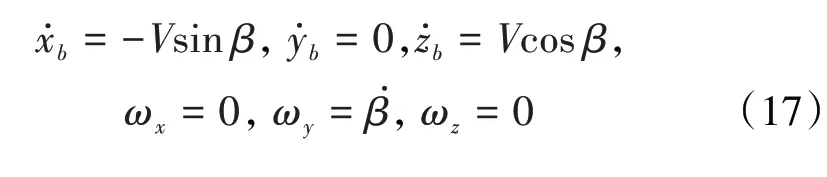
4 机动飞行下磁悬浮转子振动响应

4.1 磁悬浮转子系统参数

对机动飞行下磁悬浮转子振动响应进行数值分析，使用的转子模型是1个单盘柔性转子，工作转速为9000 r/min，不平衡质量位于刚性圆盘上，不平衡量为300 g·mm。转子由2个使用PD控制的径向磁悬浮轴承支承，具体参数见表1。转子在正常工作时悬浮于空中，当振幅过大时，可能会与磁悬浮轴承产生碰撞，引起转子失稳，所以在响应分析过程中，重点考察磁悬浮轴承处转子的振动。

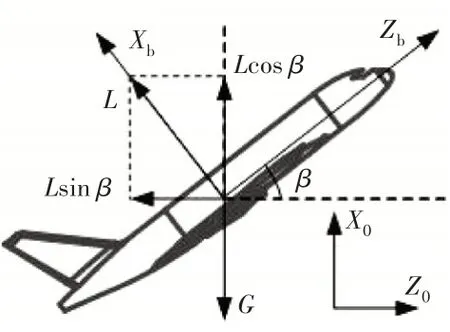
图8 飞机拉升过程受力

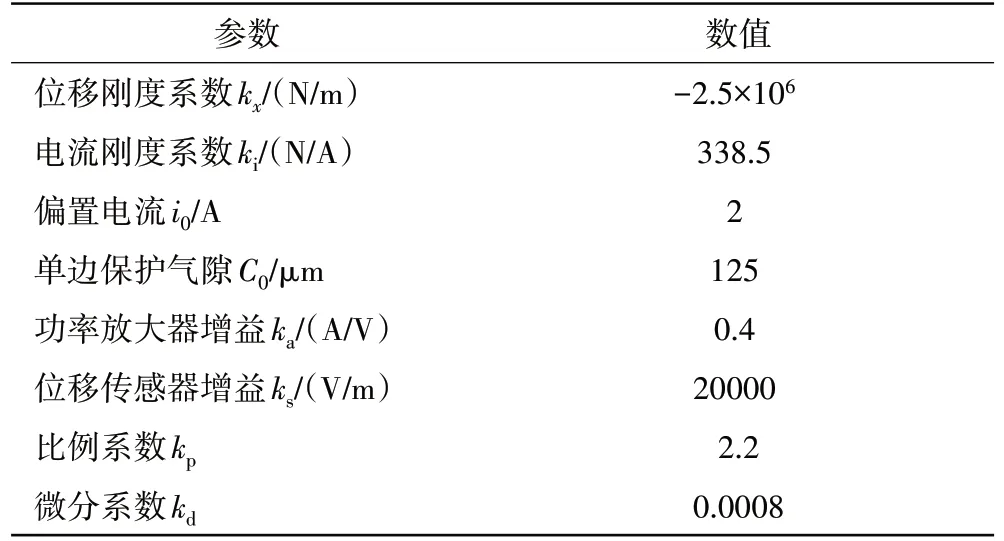
表1 磁悬浮轴承系统参数

4.2 飞机转弯时磁悬浮转子振动响应

假设飞机水平巡航的速度=150 m/s，转弯半径=2000 m，时间历程=1 s，=2 s，=4 s，=5 s，=6 s。在右转弯过程中偏航角速度̇为

在飞机右转弯机动飞行过程中转子振动响应如图9所示。从图中可见，转弯过程引起了转子在水平方向和垂直方向的偏心，使得转子的最大振幅变大，若转弯半径过小或转弯速度过大，使偏心进一步增大，严重时会与磁悬浮轴承碰摩，引发事故。

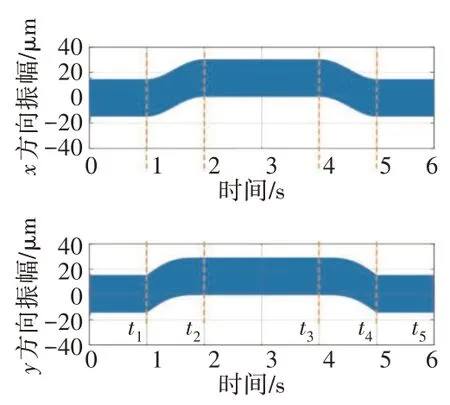
图9 右转弯机动飞行过程中转子振动响应

转弯各阶段具体的转子轴心轨迹如图10所示。从图中可见，在第0～1 s时，飞机稳定向前水平飞行，是1个稳态过程，转子只受不平衡力激励作用，转子轴心轨迹为圆，振幅为14.5μm，进动中心在磁悬浮轴承中心；在第1～2 s时，飞机开始滚转和偏航，滚转角和偏航速度不断增大，由基础运动引起的附加载荷使得转子进动中心不断向和正方向移动，即进动中心偏心不断增大；在第2～4 s时，飞机滚转角不变，偏航角速度不变，转子进动中心保持在最大偏心处，此阶段转子的振动达到最大30.2μm；在第4～5 s时可以视作第1～2 s时的逆过程，飞机滚转角逐渐减小至0，偏航角速度同步减小至0，转子进动中心逐渐回到磁悬浮轴承中心；在第5～6 s时飞机回到水平直飞状态，轴心轨迹与第0～1 s时的相同。

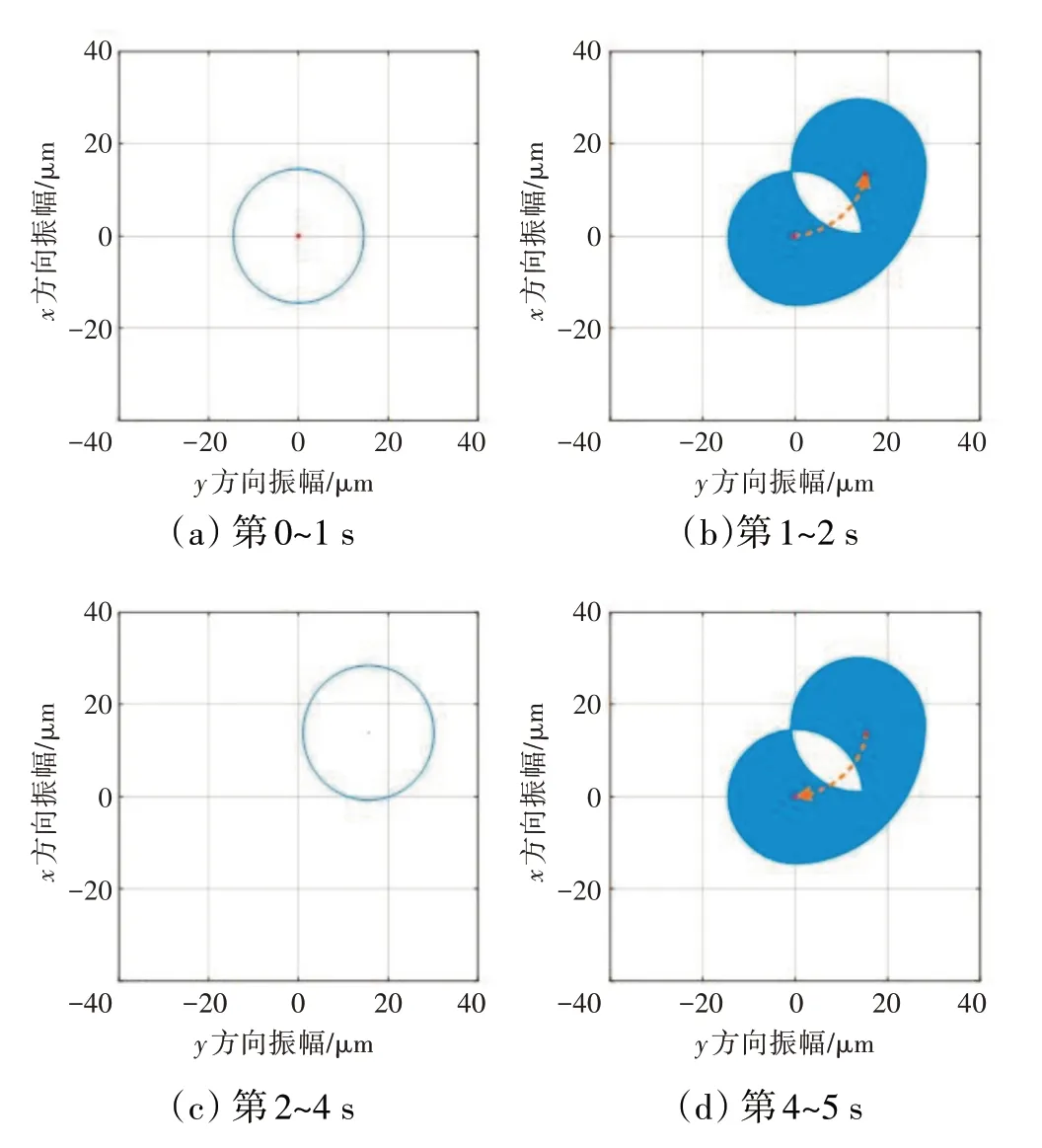
图10 右转弯机动飞行过程中转子轴心轨迹

以上分析中磁悬浮轴承使用PD控制，实际应用中会使用比例-积分-微分（Proportional Integral Derivative，PID）控制。当使用PID控制时，飞机在右转弯过程中转子振动响应如图11所示。从图中可见，在整个过程中转子振动没有出现较大的变化，即飞机右转弯工况对转子振动几乎没有影响。这是因为在右转弯过程中，飞机运动给磁悬浮转子带来的附加载荷可以看作是频率极低的扰动，而磁悬浮轴承控制器中的积分环节对低频信号跟踪能力强，系统稳态误差几乎为0，转子可以保持悬浮于轴承中心。但是相应地，磁悬浮轴承需要提供更大的控制电流以产生更大的电磁力来抵抗机动飞行的影响，当机动飞行过于剧烈时，控制电流可能饱和，引起转子失稳。

图11 在右转弯机动飞行过程中转子振动响应（PID控制）

4.3 飞机俯冲拉升时磁悬浮转子振动响应

设飞机水平巡航的速度=150 m/s，在俯冲拉升过程中飞机飞行半径=2000 m，时间历程=1 s，=2.4 s，=3 s，=4 s，=4.6 s，=6 s，=7 s。飞机在俯冲拉升运动过程中的俯仰角速度̇为

在飞机俯冲拉升机动飞行过程中转子振动响应如图12所示。从图中可见，由于俯冲拉升过程是在垂直面内进行的，对方向的振动影响较大，随着俯冲拉升过程的进行，转子进动中心位置也在不断变化。俯冲拉升过程各阶段的转子轴心轨迹如图13所示。从图中可见，在第0～1.0 s时，转子只受不平衡力激励作用，转子振动响应为不平衡响应，轴心轨迹为圆，振幅为14.5μm；在第1～2.4 s时，飞机开始向下俯冲，俯仰角速度由0先减小再增大，在第2.4 s时回到0，相应地，转子进动中心在方向的偏离先增大再减小，最大振动为25μm，受陀螺力矩耦合作用，在方向上也会有同样现象，但由于陀螺力矩较小，偏心很小；在第2.4～3.0 s时，飞机俯仰角速度为正且不断增大，转子进动中心继续朝着负方向变化；在第3.0～4.0 s时，飞机由俯冲向拉升过渡，在该过程中俯仰角速度保持不变，转子进入稳定状态，最大振动为25μm；之后的拉升过程皆为对应俯冲过程的逆过程，在转子响应上也具有相似性。与右转弯机动飞行类似，当改用PID控制后，磁悬浮轴承会以增大控制电流的方式减小飞机俯冲拉升带来的影响。

图12 在俯冲拉升机动飞行过程中转子振动响应

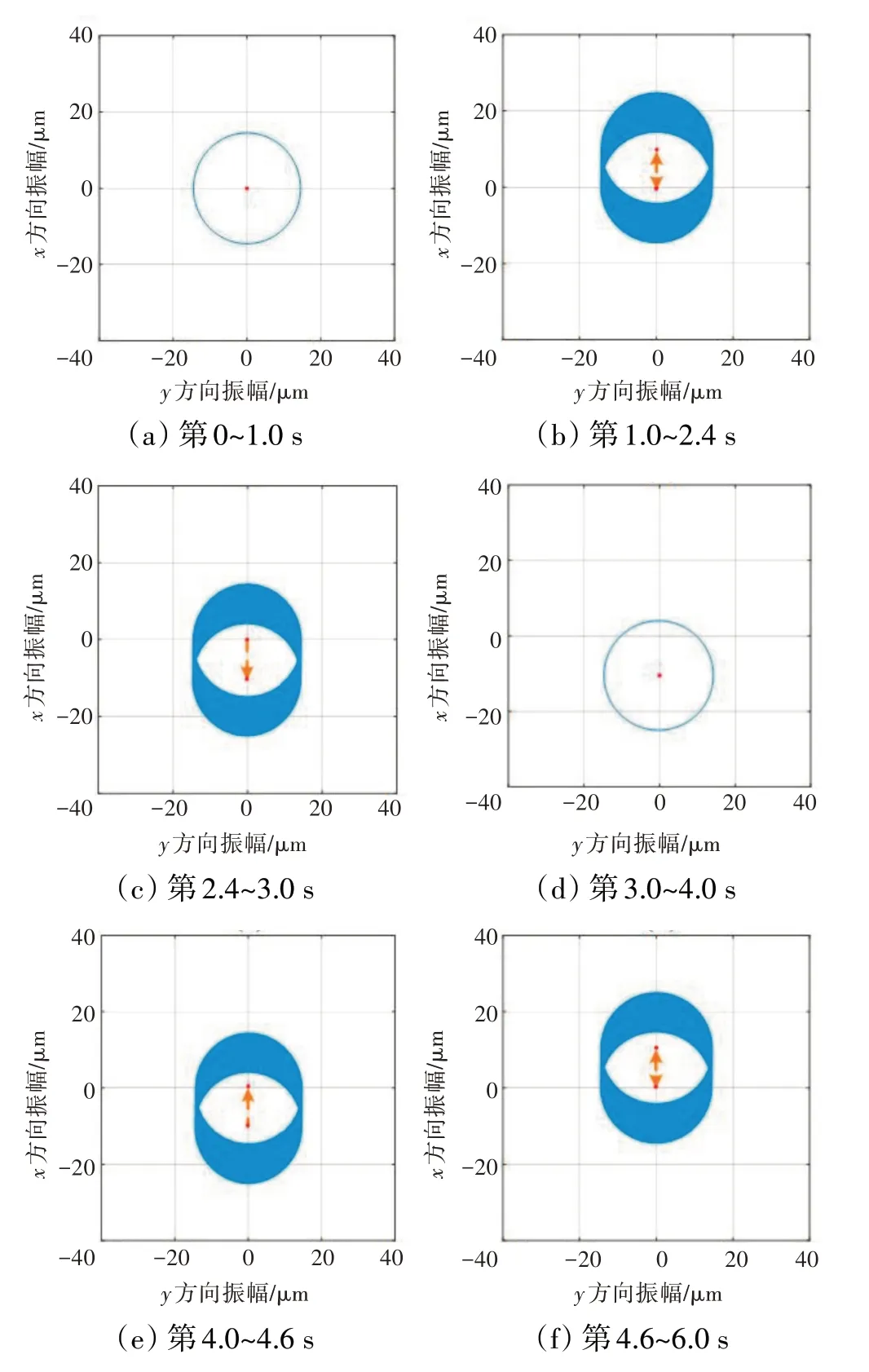
图13 俯冲拉升机动飞行各阶段转子轴心轨迹

5 结论

（1）通过数值仿真可知，当磁悬浮轴承采用PD控制时，在飞机转弯和俯冲拉升运动过程中，转子进动中心会偏离磁悬浮轴承中心，转子振动增大；

（2）当采用PID控制时，磁悬浮轴承可以以增大控制电流为代价减小转弯和俯冲拉升给转子带来的影响。

（3）在设计机载磁悬浮转子系统时，要充分考虑机动飞行带来的影响，避免振动过大使得转子与磁悬浮轴承发生碰摩，同时要避免磁悬浮轴承线圈电流饱和。

未来将进行磁悬浮轴承控制方法及控制参数对转子振动响应影响的研究，发挥磁悬浮轴承主动振动控制的优势，为磁悬浮轴承在航空发动机上的实际应用打下基础。