基于平衡流形展开模型的航空发动机健康参数估计

刘硕硕，戚万领，王志涛，高楚铭

（哈尔滨工程大学动力与能源工程学院，哈尔滨 150001）

0 引言

航空发动机控制系统根据当前飞行条件和油门杆角度（Power Lever Angle，PLA）调节被控参数的设定值，如转速、压比等，闭环调节达到目标推力。但是随着发动机长时间服役，造成叶片积垢、叶尖磨损、高温蠕变，从而使发动机部件性能退化，PLA与推力等参数的对应关系改变，以至无法实现目标推力。为实现发动机推力恢复，需探究有效的发动机状态参数估计方法，对部件健康参数进行准确评估。自20世纪80年代以来，国内外基于发动机线性模型和部件级非线性模型开展了多种优化估计算法研究，其中尤以卡尔曼滤波估计算法使用最为广泛。基于线性状态空间模型的标准卡尔曼滤波参数估计最早成功使用。在全包线内运行时，通过将设计好的各稳态点卡尔曼增益预先存为矩阵，进行插值调度使用。但由于状态空间模型为线性化近似模型，对非线性系统动态特性近似有限，当其进行多个健康参数退化估计时，虽能定位到退化部件，但却存在较大的稳态误差；而基于部件级模型的非线性卡尔曼滤波参数估计则受限于部件级模型复杂程度，计算量大、实时精度差，早期根本无法作为机载模型使用。平衡流形展开（Equilibrium Manifold Expansion，EME）模型的提出，则可有效弥补线性空间模型以及部件级模型的不足。

EME模型是1个原非线性系统的近似非线性模型，与线性模型相比具有良好的近似性。2011年，赵辉对此模型进行全面分析，界定了与其他模型的联系与区别之后，基于EME模型开展控制算法研究，并逐渐成为热点；吕铖坤、马欣彤在其后将该模型应用于控制领域，也佐证了该模型具有良好的适用性和较大的应用潜力。然而，EME模型在参数估计方面的应用研究却鲜有报道。2013年，陈可尝试用未考虑退化的EME模型代替部件级模型进行气路故障诊断，但其采用线性卡尔曼滤波器进行估计，忽略了平衡流形模型为非线性模型这一事实；此外，只给出了单个健康参数退化时的估计结果，而对发动机运行过程中最常见的参数退化方式——多健康参数同时退化并未进行讨论。

本文基于EME模型采用非线性卡尔曼滤波器进行多个健康参数退化估计。

1 平衡流形展开模型

1.1 平衡流形展开模型建模理论

在飞行条件一定时，航空发动机的非线性系统方程为

式中：x∈R，为状态向量；u∈R，为控制向量；y∈R，为输出向量；f和g为连续可微的非线性函数。

定义非线性系统（式（1））的平衡流形为系统平衡点的集合

平衡流形用调度变量α表示为

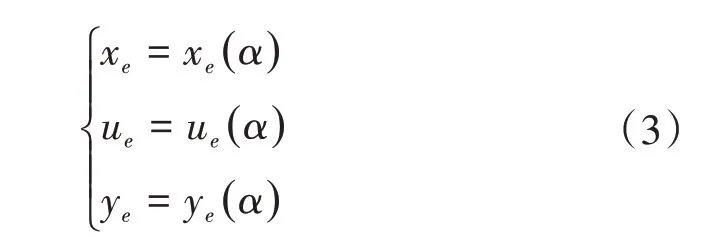
则将式（1）在由α决定的平衡点( x,u,y)处进行泰勒展开，保留1阶项，可得该点的线性化模型族

式中：A,B,C,D为4个雅克比矩阵，Δx=x-x(α)，Δu=u-u(α)。

为使式（4）成为非线性模型，需另外建立调度参数α与当前工作点( x,u,y)的联系，由于y与x和u之间为代数关系，只需建立α与x和u之间的关系式

式（5）实质是建立当前工作点(x,u,y)向平衡流形点(x,u,y)的映射。这一映射的设计具有一定的自由度，其惟一的约束要求是能够将任意稳态点映射到该稳态点本身，即α=a (x(α),u(α))。

1.2 考虑退化的涡扇发动机平衡流展开模型

在飞行条件为H=0、Ma=0时，选择如下参数来建立EME模型：

（1）x=[n,n]，分别表示低压轴转速和高压轴转速；

（2）u=[W,A]，分别表示燃油量和尾喷管喉道面积；

（3）η=[η,η,η,η]，分别表示风扇、高压压气机、高压涡轮和低压涡轮的绝热效率；

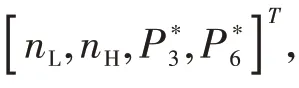
为保证数值计算的稳定性，各变量均已做相似归一化处理，限于篇幅不再详细阐述。

健康因子的作用等同于输入参数，则考虑部件性能退化的双轴涡扇发动机线性化模型族式（4）可以展开为

调度参数与输入参数同维度，取之为、、、、、，映射方程在x ()=x ;u ()=u 中任取6个，本文取为

则联立式（7）、（8）得到考虑退化的平衡流形展开模型的最终形式

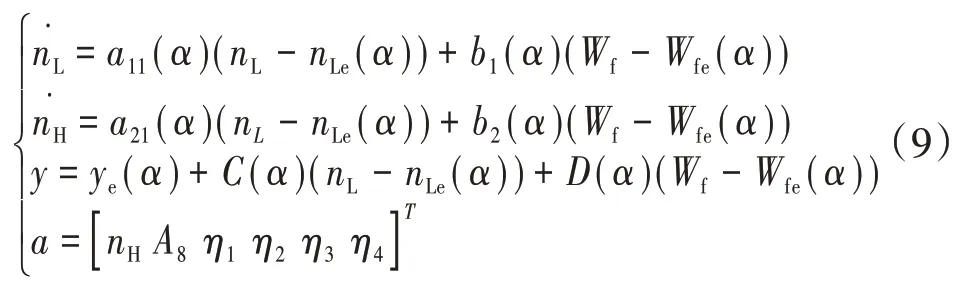
以部件级模型为基础，采用陆军等提出的线性拟合法求系数矩阵各元素值，并采用BP神经网络对平衡流形模型的动态参数、静态参数进行拟合。

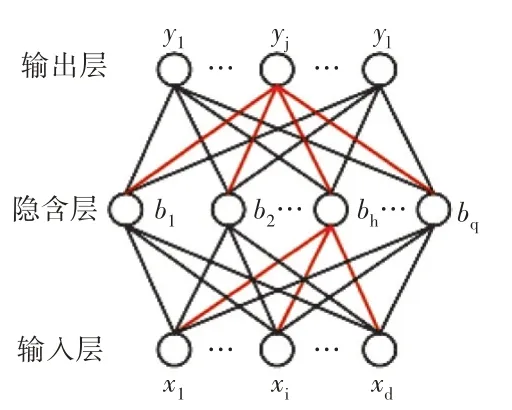
图1 神经网络结构

由于参数拟合维度过高，无法可视化展示，限于篇幅，以()矩阵为例，按一定顺序列出各点值来展示神经网络拟合结果，如图2所示。神经网络对多维非线性函数拟合具有独特优势

图2 A矩阵神经网络拟合结果

1.3 模型精度验证

模型精度直接影响参数估计结果。以最常见的多参数渐变为例，将EME模型和部件级非线性模型的仿真结果进行对比。设置如图3所示的健康因子退化过程：4种部件效率在第10 s同时开始渐变；经过10 s后，渐变分别降至1.0%、1.5%、2.0%和2.5%；再经过10 s稳定后，渐变再分别降至2.0%、2.5%、3.0%和3.5%，之后保持稳定。

图3 健康因子退化过程

以高压轴转速为例，进行EME模型与部件级模型响应对比，验证EME模型动态响应，如图4所示。从图中可见，2种模型的渐变响应基本重合。所建立的EME模型对原非线性系统具有良好的近似性，可用于健康因子退化估计。

图4 2种模型高压轴转速响应对比

2 卡尔曼滤波参数估计

卡尔曼滤波器又名最佳状态估计器，本质上是一种最小方差估计方法。通过模型的估计值与实际测量值之间的误差对状态不断更新，使得状态变量值的误差方差最小，从而得到最佳估计值。

2.1 扩展卡尔曼滤波器

扩展卡尔曼滤波（Extended Kalman Filter，EKF）是在标准卡尔曼滤波基础上发展而来的，用于非线性系统参数估计。通过将过程方程和测量方程在某状态点处进行泰勒展开，求取雅可比矩阵，得到卡尔曼增益后再利用标准卡尔曼滤波算法进行参数估计。

设有噪声的发动机离散数学模型表示为

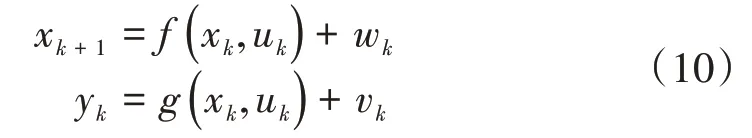
式中：和为第1.2节中建立的EME模型的系统方程和测量（输出）方程；为系统噪声，为测量噪声。

假设和都是不相关的高斯白噪声，则

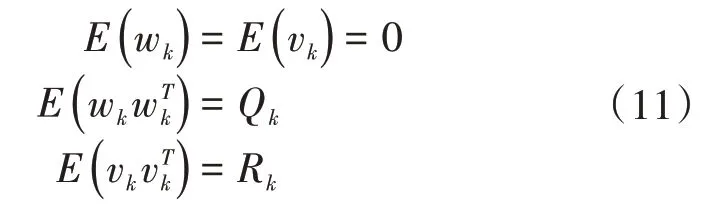
扩展卡尔曼滤波估计方程及预测方程如下：

2.2 无迹卡尔曼滤波器

无 迹 卡 尔 曼 滤 波（Unscented Kalman Filter，UKF）同样用于非线性系统估计，其基于无迹变换，通过构造1组确定的加权样本点来对估计参数进行近似。可避免对非线性模型的线性化建模及雅可比矩阵计算。UKF基本算法描述如下：

初始状态统计特性

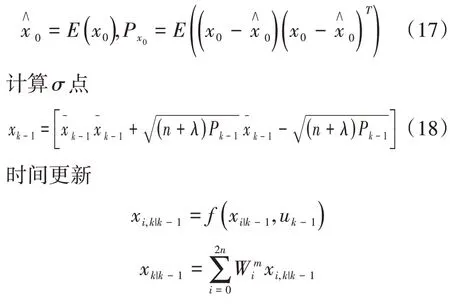
式中：W 为均值的权值；W 为协方差的权值。

3 健康因子退化估计

本章对健康因子的多种退化模式进行仿真，限于篇幅仅以多参数渐变、多参数突变为例进行验证说明，不再赘述单参数渐变、单参数突变这2种参数退化模式。

3.1 多参数渐变估计

对于可测输出参数，其传感器标准差约为0.1%～1%，本文假设都为0.2%，因此测量噪声矩阵R=([0.002,0.002,0.002,0.002])·I，系统噪声矩阵Q通过试凑法确定，采样时间为20 ms。无迹卡尔曼滤波参数取值为=0.1 ,=2 ,=0。决定点围绕均值的分布；用于合并随机变量分布的先验知识。

在实际运行中，多个健康因子同时渐变是最常见的退化模式，对此，本文设计了如下的参数渐变模式以验证参数估计的准确性：4种部件效率退化因子从第10 s起，经30 s后分别渐变至2.0%、2.5%、3.0%和3.5%，之后维持稳定。发动机的真实退化过程远大于所设定的仿真时间，设置退化时间为30 s，一方面有助于验证估计的实时精度，另一方面便于仿真模拟。EKF与UKF多参数渐变估计结果分别如图5、6所示。

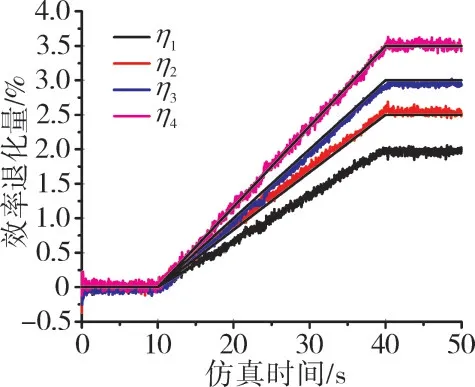
图5 EKF多参数渐变估计结果

仿真结果表明，对于多参数渐变模式，基于EME模型进行非线性卡尔曼滤波估计结果良好。利用2种非线性卡尔曼滤波器得到的估计结果基本一致。无论是EKF还是UKF，都能极好地跟踪参数渐变过程，稳态相对误差绝对值不超过3%。

图6 UKF多参数渐变估计结果

3.2 多参数突变估计

结合状态空间模型和标准卡尔曼滤波器进行多参数突变估计时，常由于线性模型近似程度低而使估计结果存在稳态误差大、退化参数定位不准等问题。本节基于EME模型，设置3种不同退化程度的多参数突变模式（见表1）来进行参数估计仿真，以验证结合EME模型和非线性卡尔曼滤波器进行参数估计的可靠性。测量噪声矩阵、系统噪声矩阵等参数与上文相同。各模式的EKF与UKF估计结果分别如图7～9所示。

表1 多参数突变退化模式

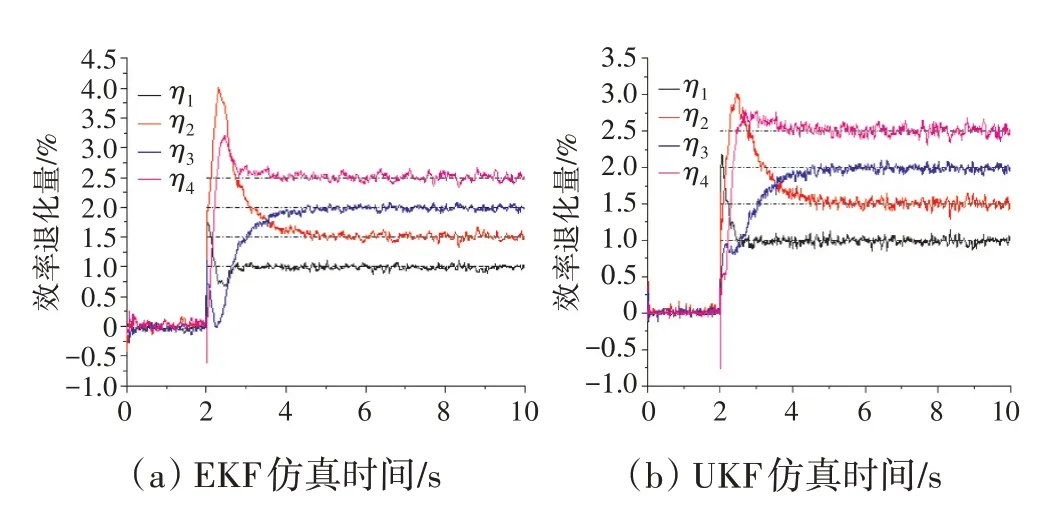
图7 EKF、UKF参数估计结果（模式1）

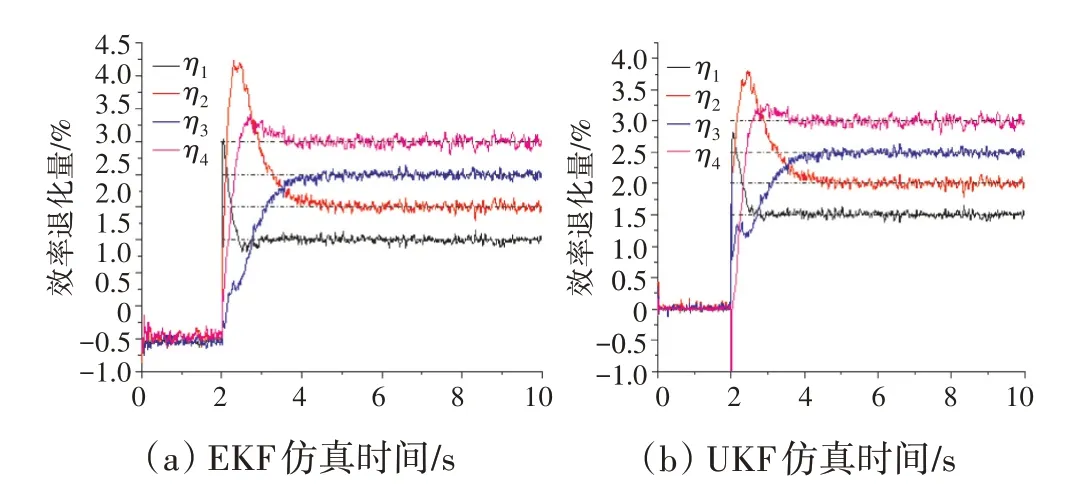
图8 EKF、UKF参数估计结果（模式2）

图9 EKF、UKF参数估计结果（模式3）

从图7～9中可见，基于EME模型，无论是采用EKF还是UKF都能迅速准确地定位到退化参数，并估计出部件性能退化程度。二者均没有出现结合线性状态变量模型和标准卡尔曼滤波估计时所存在的较大稳态误差，体现出EME模型对原非线性系统良好的近似性。此外EKF与UKF的收敛速度基本一致，均在5 s以内，但UKF的估计参数变化曲线更平稳。考虑到UKF相较于EKF更适用于对强非线性系统进行参数估计，侧面佐证了EME模型是原非线性系统的较佳近似模型。可在保证精度的情况下代替部件级模型进行健康参数退化估计。

4 结束语

（1）提出基于平衡流形展开模型结合非线性卡尔曼滤波器的方法进行发动机健康参数估计，验证了发动机健康参数估计新的模型基础。

（2）得益于EME模型对原非线性系统良好的近似性，多参数渐变、多参数突变模式参数估计结果准确高效，稳态误差不超过3%，弥补了线性状态模型近似性差、部件级模型计算量大等不足。为基于EME模型构建机载自适应模型奠定了方法基础。

（3）当退化参数较多，并且需建立整个飞行包线内的EME模型时，系数矩阵求解、调度参数拟合等方面工作量大，需进一步探索更为高效的方法。