铝蜂窝夹层结构等效模型在低速冲击仿真中的应用

李宗权，张胜兰，杨稳

（湖北汽车工业学院 汽车工程学院，湖北 十堰 442002）

蜂窝夹层结构由面板、轻质芯材以及中间粘合剂层组成，具有密度低、强度高、隔音好及优异的耐碰撞性和能量吸收能力等特点［1］，广泛应用于航空航天［2］、汽车工业［3］和船舶［4］等领域。在日常使用中，蜂窝夹层结构容易受到外来物品低速冲击的影响，导致材料性能降低。用有限元软件对蜂窝夹层结构低速冲击过程进行研究，可以为蜂窝夹层结构的性能校核及结构设计提供设计依据。国内外学者对蜂窝夹层结构在低速冲击下的动力学响应进行了大量的研究。Recep等［5］利用落锤冲击试验系统测量冲击过程中的接触力和变形，建立了铝蜂窝夹层结构有限元模型。齐佳旗等［6］基于文献［5］中的模型发现蜂窝芯单元尺寸越大，夹层板的刚度和稳定性越低，蜂窝芯的高度对吸能的影响较小。谢鑫等［7］发现随着冲击角度的增大，铝蜂窝夹层结构的最大损伤深度减小，上面板的变形减小，下面板几乎没有变形，沿着冲头冲击方向的蜂窝芯单元屈曲增多，但损伤程度减轻。Liu等［8］采用Abaqus/Explicit方法在铝蜂窝芯中填充圆形管更能提升蜂窝夹层结构的抗冲击能力，但是并没有考虑面板与蜂窝芯之间的胶粘剂层，因此预测的夹层板塑性吸能值被低估。Zhang等［9］分别构建了考虑胶层以及没考虑胶层的铝蜂窝夹层结构冲击模型，发现考虑粘接层的模型比不考虑粘接层的模型得到的结果更准确。Sharunov［10］等使用Abaqus软件的二维Hashin 失效准则对复合材料蜂窝夹层结构损伤模型进行了仿真分析。Wang等［11］利用蜂窝夹层结构低速冲击模型的对称性，对模型的1/4 进行建模，减小了模型的尺寸和运行分析时间。目前对于蜂窝夹层结构低速冲击下的动态响应研究文献较多，但较少有建立蜂窝夹层结构等效模型进行动力学分析。文中基于三明治夹芯板理论、Y模型理论简化蜂窝夹层结构，并进行低速冲击仿真，与详细模型仿真结果进行对比，验证等效模型的仿真精度。

1 蜂窝夹层结构详细仿真模型

基于文献［5］的试验及有限元模型，建立蜂窝夹层结构的低速冲击详细模型，铝蜂窝芯采用Al 3003-H19 铝箔由胶结拉伸法粘接而成，结构如图1所示。材料的力学参数如表1所示。冲击所用冲头为半球型，直径为20 mm，质量为5.045 kg。建立了内径为40 mm，外径为80 mm，厚度为2 mm 的圆形夹紧环来约束蜂窝夹层结构的自由度。在面板和蜂窝芯之间设置Tie 约束，限制夹紧环所有的自由度，并且冲头只保留Z轴方向的移动自由度。在冲头和上面板之间建立面面接触，令冲头的外表面为主面，上面板为从面。面面接触的法向设置为硬接触，切向设置为罚函数接触，其摩擦系数设为0.5。为了防止冲击过程中部件与部件之间发生穿透干涉问题，设置通用接触，法向设置与切向设置与面面接触的设置保持一致。

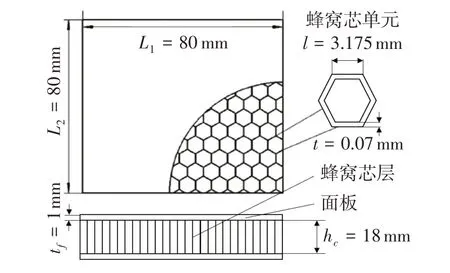
图1 蜂窝夹层结构示意图

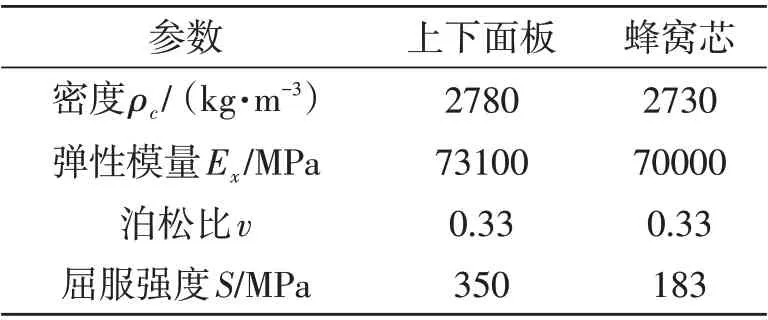
表1 铝面板和铝蜂窝芯的材料参数

上下面板采用Solid 材料属性，蜂窝芯采用Shell材料属性，冲头以及约束环为刚体材料模型。为了与Recep［5］的试验以及仿真模型保持一致，将蜂窝夹层结构低速冲击详细有限元模型的网格尺寸设置为1 mm，建立的详细有限元模型见图2。

图2 蜂窝夹层结构详细模型

2 蜂窝夹层结构等效模型

2.1 三明治夹芯板理论

三明治夹芯板理论将面板和蜂窝芯分开考虑，将面板等效为服从Kirchhoff假设的均质薄板，蜂窝芯等效成正交各向异性的均匀连续结构［12］。根据蜂窝芯结构的几何特征和材料属性，确定蜂窝芯的等效参数［13-14］，蜂窝芯为正六边形，等效参数为

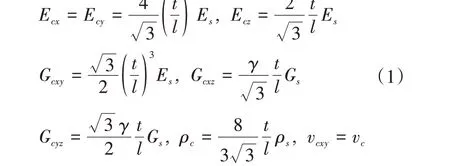
式中：Es为弹性模量；Gs为剪切模量；ρs为密度；vs为泊松比；t为壁厚；l为六边形蜂窝外接圆半径；γ为修正系数，取0.4～0.6；Ecx、Ecy、Ecz为3个方向的等效弹性模量；Gcxy、Gcyz、Gcxz为3个坐标面内的等效剪切模量；ρc为蜂窝芯的等效密度；vcxy为蜂窝芯在xoy面内的等效泊松比。

2.2 Y模型理论

目前大部分蜂窝芯都是采用制造工艺比较简单的胶结拉伸法制成，导致蜂窝在沿Y轴方向上的壁厚是其他四边壁厚的2倍，而蜂窝芯的Y模型理论解决了该问题［15］。正六边形双壁厚蜂窝芯Y模型等效参数［16］：

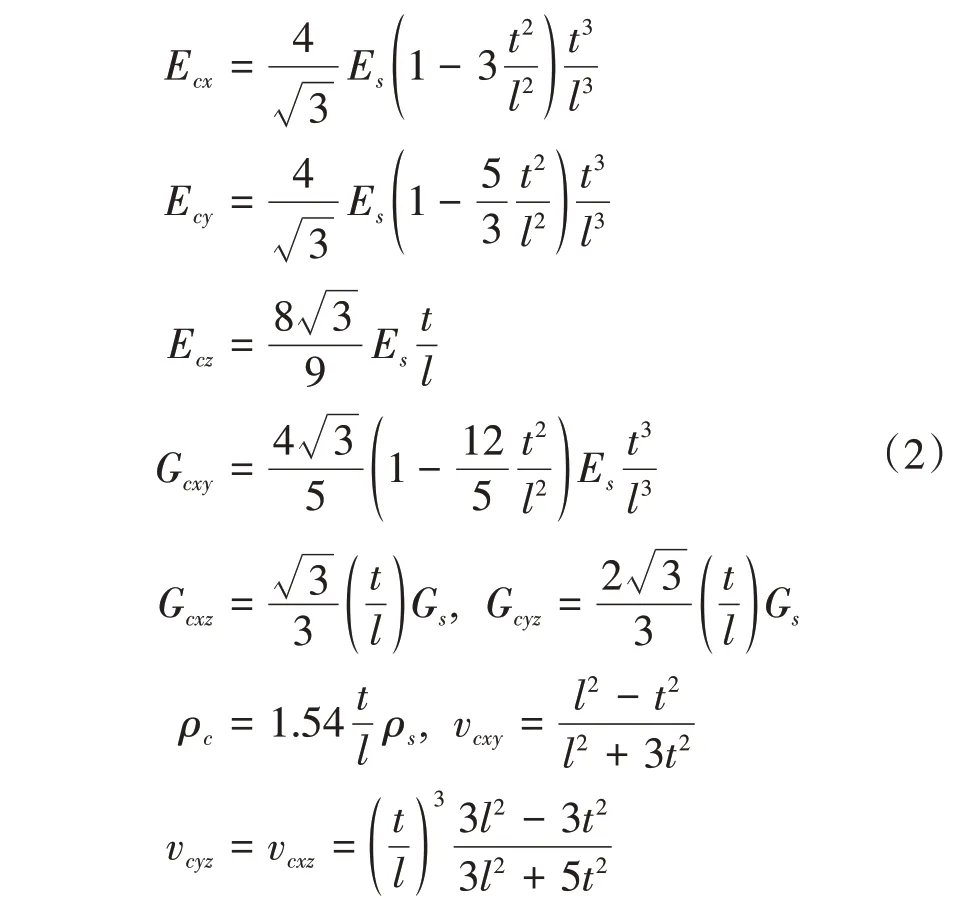
式中：vcyz为蜂窝芯在yoz坐标面内的等效泊松比；vcxz为蜂窝芯在xoz坐标面内的等效泊松比。

2.3 等效模型构建

蜂窝夹层结构等效模型的设置及约束与蜂窝夹层结构详细模型保持一致，冲头以及约束环采用刚体材料模型。由于三明治夹芯板理论计算出的泊松比只有xoy方向的参数，因此将三明治等效模型的蜂窝芯赋予层合板属性，而Y等效模型赋予工程常数属性，2种等效模型所采用的材料参数如表2所示。在有限元仿真中，等效模型的网格尺寸设置为3 mm，建立的蜂窝夹层结构等效有限元模型如图3所示。

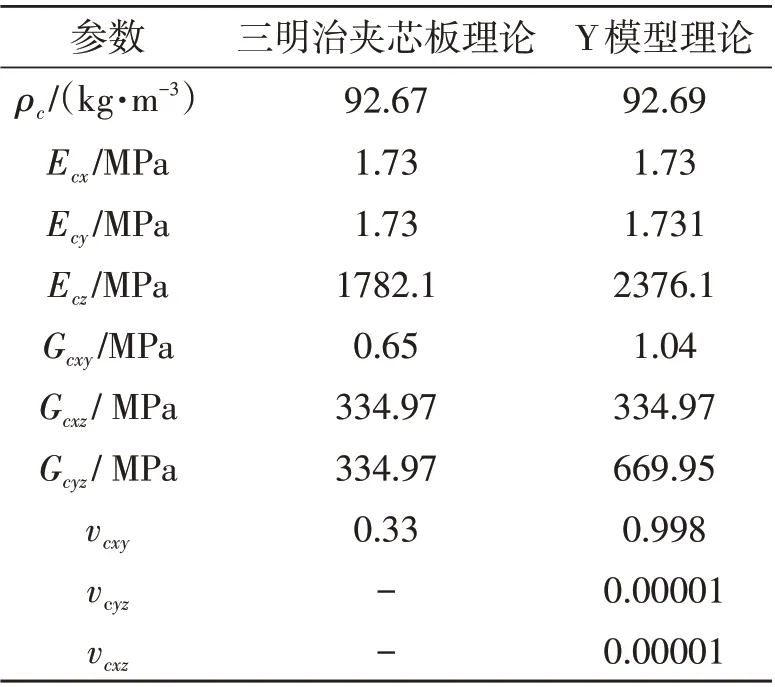
表2 等效模型的材料参数

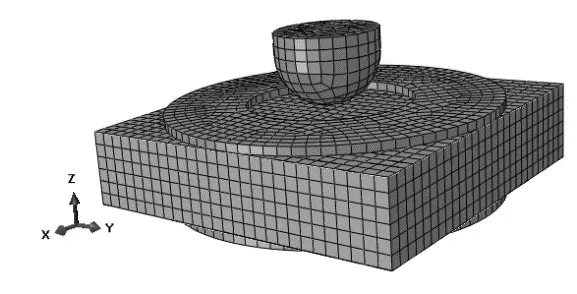
图3 蜂窝夹层结构等效模型

3 模型验证

3.1 接触力时间曲线

搭建了蜂窝夹层结构低速冲击的详细有限元模型，与三明治等效模型及Y等效模型进行仿真对比。在其他参数相同的情况下，冲击能量E分别为41.95 J、59.78 J、81.07 J时，详细模型与等效模型的接触力时间曲线如图4所示。

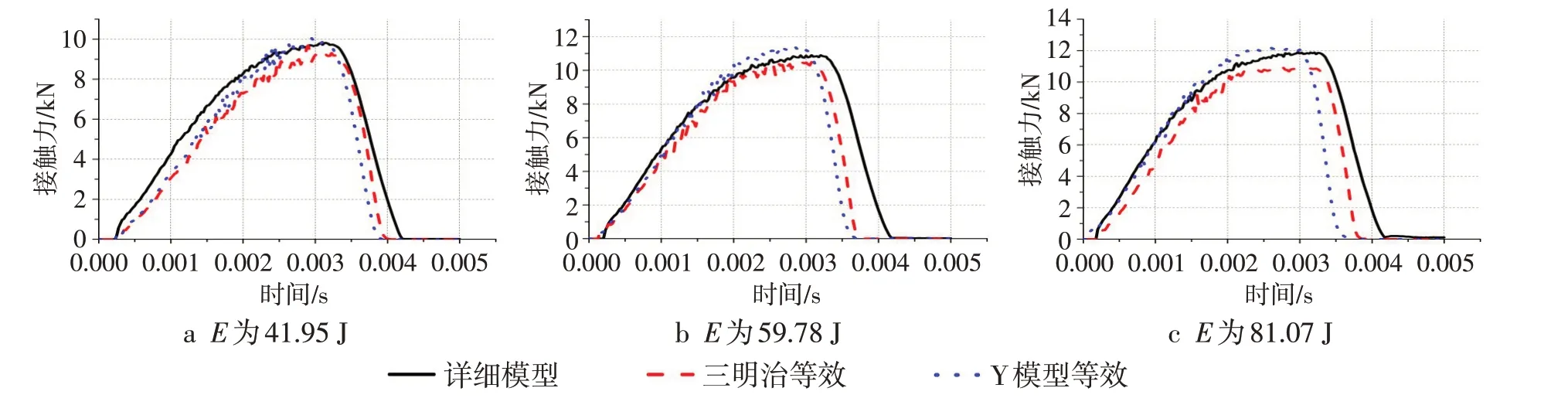
图4 不同冲击能量下3种模型接触力变化曲线

通过对比详细模型与等效模型数据可知，在3种不同冲击能量的作用下，详细模型接触力峰值分别为9.81 kN、10.80 kN 和11.89 kN，三明治等效模型接触力峰值分别为9.76 N、10.53 kN和10.94 kN，Y 模型的接触力峰值分别为10.05 kN、11.38 kN 和12.19 kN。计算可得，三明治等效模型和详细模型接触力峰值的偏差分别为0.56%、2.53%和8.03%，Y 等效模型和详细模型接触力峰值的偏差分别为2.45%、5.39%和2.43%。

3.2 接触力时间曲线

蜂窝夹层结构详细模型与三明治等效模型、Y等效模型在3 种不同冲击能量作用下的冲击损伤深度对比，如图5～7所示，可以看出：三明治等效模型的损伤深度普遍比详细模型偏大，三明治模型和详细模型损伤深度的偏差分别为5.75%、2.81%和2.84%；而Y 等效模型的损伤深度都比详细模型要小，Y等效模型和详细模型损伤深度的偏差分别为1.7%、1.62%和3.48%。Y 等效模型对于冲击损伤深度的计算更加精确。

图5 不同冲击能量下详细模型冲击深度

综上可知，所建立的铝蜂窝夹层结构等效有限元模型能够较为准确地预测冲击后的铝蜂窝夹层板的损伤变形和动力学响应。

图6 不同冲击能量下三明治等效模型冲击深度

图7 不同冲击能量下Y等效模型冲击深度

4 结论

将蜂窝夹层结构的等效模型应用到低速冲击中，分别将三明治夹芯板等效模型和Y等效模型应用到铝蜂窝夹层结构的低速冲击动力学仿真中，比较了不同冲击能量下的3 种铝蜂窝夹层结构模型的表现。整体上来说2 种等效模型的冲击损伤深度与详细模型较为接近，但是三明治模型的接触力峰值普遍比详细模型要小，Y模型的接触力峰值普遍比详细模型要大。