双SCARA机器人运动模型仿真与控制系统

潘广通，李慧玲，杨畅畅，姚天胜，王佳维

（湖北汽车工业学院 电气与信息工程学院，湖北 十堰 442002）

相比单个机器人，双机协作机器人对环境表现出更强的适应能力，具有更强的灵活性和鲁棒性，可以更加出色地完成作业任务［1］。经过几十年的迅速发展，双机协作机器人的研究取得了较多成果。李猛等［2］对双机协作空间进行了求解与仿真分析，为双机器人避让问题提供了理论依据。李鹏飞等［3］对理想环境下双机器人运动路径进行了规划，为工业实际应用提供了理论基础。王文林等［4］对双机器人系统协调搬运作业进行了实验分析，水平和垂直方向的运行精度均控制在±2.8 mm以内。文中以2 台三自由度SCARA 机器人为研究对象，针对双机器人协作搬运时的干涉问题，建立运动学模型，制定双机协调工作任务，开发上位机人机交互界面和双机避让程序，控制机器人运行。

1 方案设计及模型建立

1.1 方案设计

采用D-H 法建立双机协作机器人运动学模型，通过MATLAB 编程求解双机协作机器人的协调工作空间。以PLC 为下位机控制器，对SCARA机器人进行逻辑控制，制定双机协作机器人协调工作任务。基于C#开发的运动控制上位机根据协调工作空间选择双机协作机器人避让程序，使双机协作机器人在工作空间内稳定运行。PLC设备、上位机之间进行双向通信，上位机向PLC 发送命令，PLC反解程序将位置数据转换为脉冲，控制机器人运动，PLC 正解程序将脉冲转换为位置数据，通过上位机实时显示。系统总体结构如图1所示。

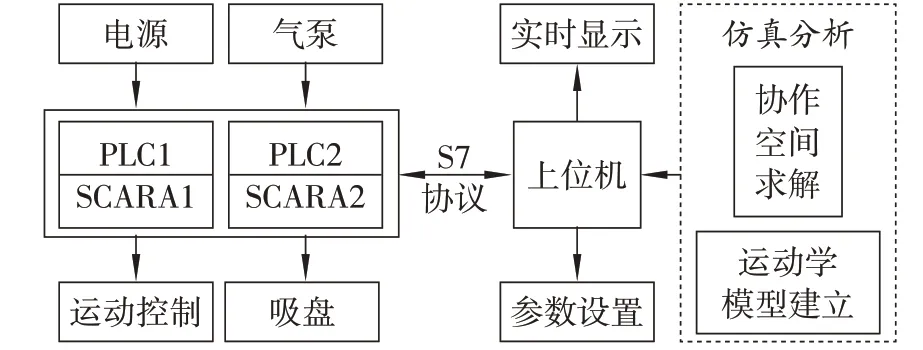
图1 系统总体结构图

1.2 运动学模型建立

为了对双机协作时的干涉问题进行分析，建立了双机协作机器人运动学模型。对2 台相同型号的SCARA 机器人运用D-H 法建立连杆坐标系，以1 号机器人基坐标系作为双机器人系统的世界坐标系。双机协作机器人位姿约束方程［5］为

式中：T3A为1号机器人基坐标A到末端的位姿变换矩阵；T3B为2号机器人基坐标B到末端的位姿变换矩阵；T0为A到B的齐次变换矩阵。根据式（1）可确定每个插补点的约束方程。以1号机器人为例，建立连杆坐标系如图2所示，机器人D-H参数如表1所示，ai为第i个关节的连杆长度，αi为第i个关节的扭角，di为第i个关节的移动范围，θi为第i个关节旋转角度。

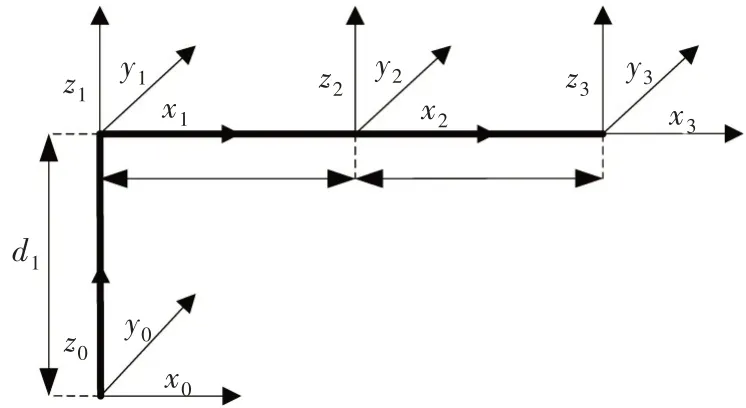
图2 连杆坐标系

表1 SCARA机器人D-H参数表

1.2.1 机器人运动学求解

正运动学问题是已知初始给定的各关节转动角度及关节参数，求解末端坐标系在基坐标系下的位姿［6］。根据机器人学的连杆变换求解正运动学，将各连杆变换矩阵相乘，得到SCARA 机器人的末端变换矩阵：

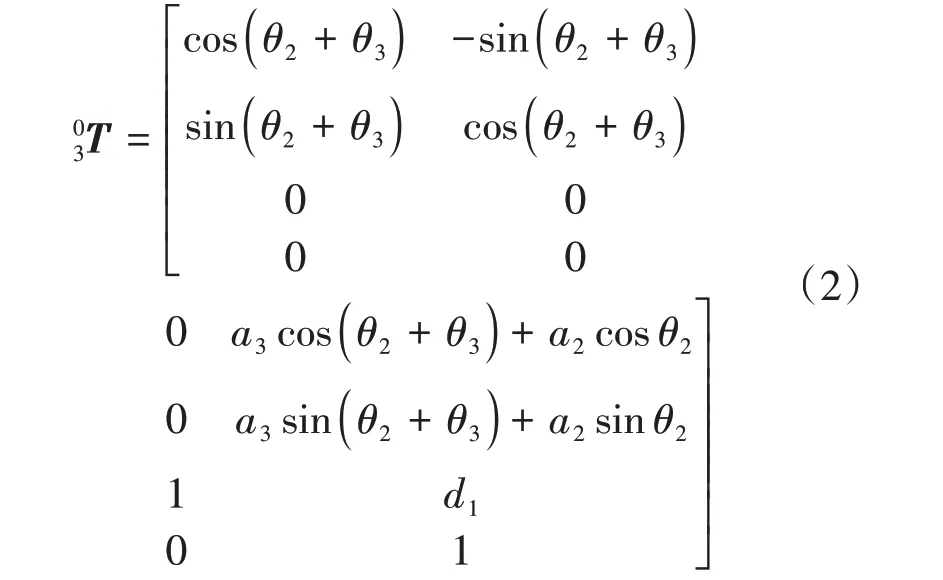
式（2）描述了末端连杆坐标系x3y3z3相对于基坐标系x0y0z0的位姿，在给定D-H参数的情况下，通过正运动学求解，机器人工作空间范围内的任意位姿均可用末端变换矩阵表示。

机器人的逆运动学问题是根据已知机械臂末端的位姿，反推各个关节到达期望位姿时的角度值［7］。求解机器人逆运动学的方法主要有几何法、逆变换法和解析法，文中采用逆变换法，其计算速度快，便于实时控制。机器人末端相邻关节位姿的逆矩阵间关系为

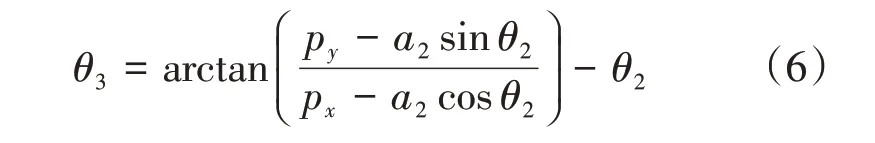
式（5）中θ2、θ3即SCARA 机器人的运动学逆解，均在机器人工作空间范围内，控制各关节角与逆解相同，可到达期望位姿。

1.2.2 双机器人关节模型与协调工作空间

机器人的大臂长21.5 cm，小臂长21.5 cm，升降臂变化范围为0～30 cm，大臂旋转范围为-180°～0°，小臂旋转范围为-135°～135°，2个机器人间相距78 cm。MATLAB 中双机器人关节模型根据SCARA 机器人实际参数建立，其仿真效果与实际工况理论上一致，模型如图3所示。

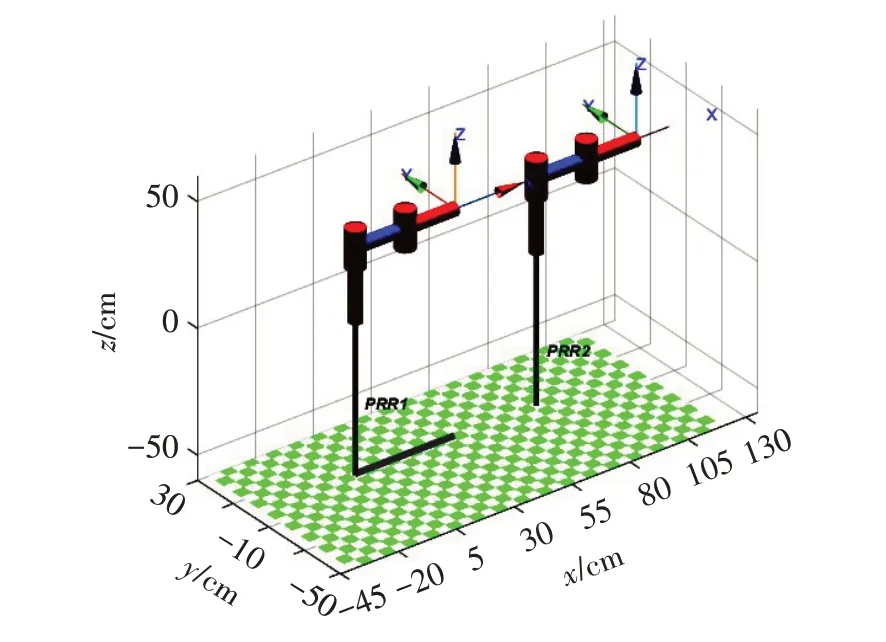
图3 双SCARA关节模型

工作空间指机器人末端执行器能够到达的工作范围［8］。文中采用蒙特卡罗法求取双SCARA 机器人的协作空间，在Robotics toolbox工具箱中运用蒙特卡罗法求取双机器人工作空间。根据正运动学方程解出机器人末端坐标（px，py，pz）,用Rand 函数产生关节角度变量随机值：

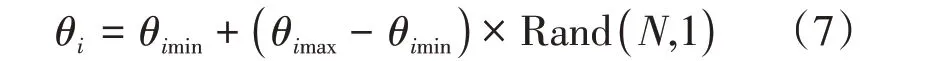
式中：θimin为第i个关节的最小转动角度；θimax为第i个关节的最大转动角度；N为生成的随机点的数量，取值100 000。利用MATLAB软件，用打点的方式画出1～2号机器人的工作空间，如图4所示。重叠部分为双机协调工作空间，由图4可得双机器人协作空间为x∈［35,43］，y∈［-18,12］，z∈［0,30］。

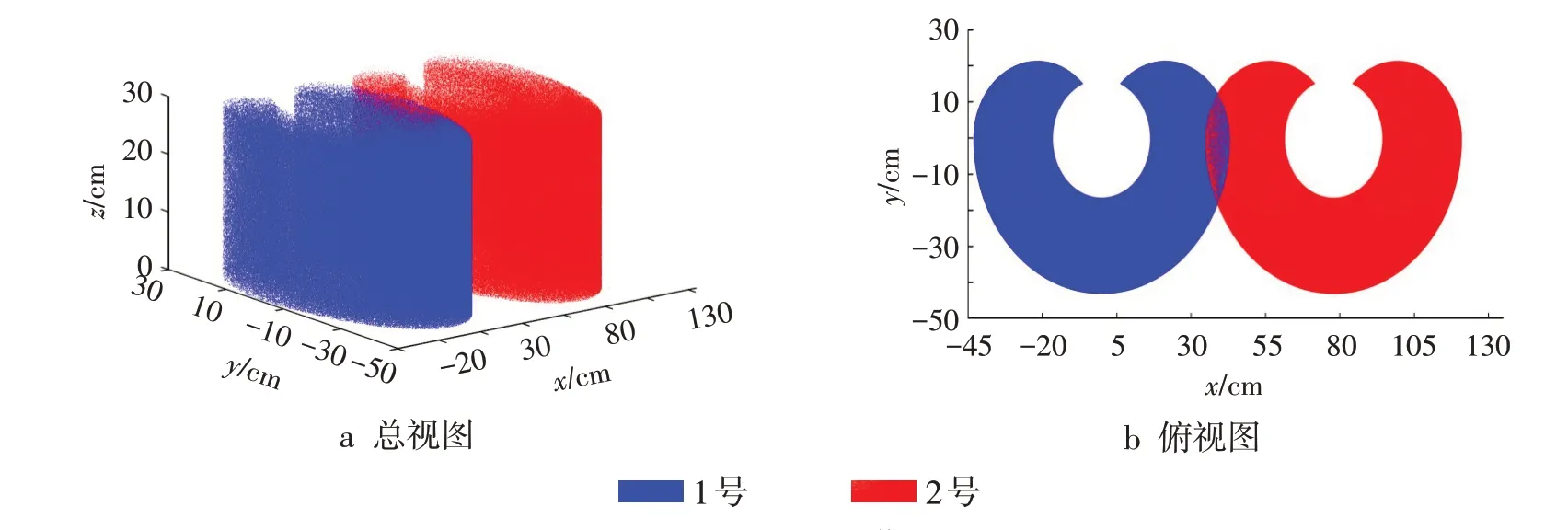
图4 双机器人工作空间

2 双机器人系统控制设计

2.1 控制系统方案设计

控制系统主要由SCARA机器人、西门子PLC、末端气动吸取装置及上位机组成。PLC 负责控制机器人的动作运行，上位机负责实现双机器人自动避让功能和实时显示机器人运动过程中的位置信息。在双机器人协作搬运物料过程中，要求1号机器人末端气动装置夹持物料至协调工作空间内指定位置，放下物料后返回，2 号机器人到上述指定位置取料。采用2台实验室三自由度SCARA 机器人构成协作平台，完成协调搬运作业。

整个控制系统分为2 级，第1 级为上位机与双机器人控制器间的通信与控制，第2 级为2 个PLC控制器对各自机器人本体的控制。将2 台PLC 通过以太网与计算机相连，基于C#编写的上位机通过S7协议与PLC建立通信，采集解析PLC数据，在上位机界面显示，通过上位机向PLC 发送命令，PLC反解程序将平面位置数据转换为脉冲，通过驱动器发送给步进电机，步进电机将脉冲信号转换为角度信号，控制机械臂各轴运动。

2.2 PLC程序设计

根据实际工况，在博图软件运动控制向导中组态速度参数，通过设置合理的加减速参数和急停时间参数，使设备平稳运行。由于步进电机通过脉冲转换为步距角，控制机器人动作，因此选择脉冲作为度量单位，机器人步进电机初始步距角为1.8°，为保证机器人的运行精度，设定关节3驱动器8细分，结合机器人自身传动比，修改后关节3 步进电机步距角为0.028°；根据逆运动学求解时多移动小关节少移动大关节原则，设定关节2 驱动器16 细分，修改后关节2 步进电机步距角为0.014°。经运动学正解计算，机器人末端水平X方向运行精度为±0.065 mm，水平Y方向运行精度为±0.25 mm，运行精度高，运动可靠。双机器人系统各关节运行参数，如表2 所示。PLC 程序采用模块化编程，程序由1个主程序和若干个子程序组成，通过主程序和子程序的互相配合，使2个机器人按照设定路径循环运动［9］。功能子程序包括轴初始化程序、建立零点程序、手动控制程序、自动控制程序、反解程序和正解程序。图5为双机器人协调运动实物图。

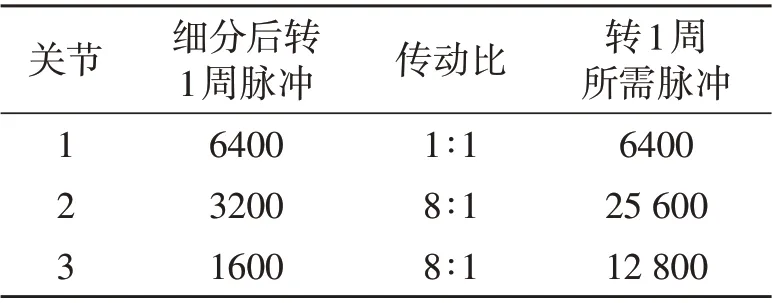
表2 各关节参数

图5 双机器人协调运动

2.3 上位机功能设计

上位机开启2 个线程，分别与2 台PLC 建立通信。上位机作为客户端，PLC 作为服务端，服务端先在内核中创建socket结构体，使当前进程与网卡建立联系，然后绑定IP地址和端口号，主动监听该端口，处理监听状态。客户端向服务端发送报文，进行连接请求，等待服务端回复报文，接受请求，建立客户端连接，客户端确认连接建立后，完成握手。实现客户端对服务端位置数据的读写，程序运行完成后关闭socket，将资源释放。上位机连接PLC设备后，需要定时循环读取PLC数据。为保证数据实时有效，在上位机与下位机通信成功后，开启1 个线程不断地读取下位机数据。为解决上位机读写操作时的资源共享问题，在上位机读写程序中创建线程锁，确保写操作程序运行时不会被读取线程中断，避免上位机崩溃，直到该代码块运行完成后，释放该线程锁［11］。

上位机界面如图6 所示，从功能上可划分为4个部分：初始化操作，包括连接PLC，设置IP 地址、端口号、显示当前连接状态等；实时显示，可以实时显示机器人的位置信息；参数修改，可以改变机器人各关节的位移值和速度值；运动控制，能够控制机器人自动运行、点动运行、回归原点等操作。

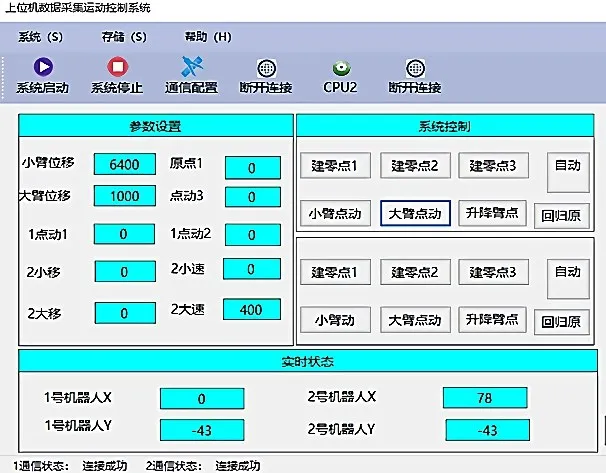
图6 上位机界面

2.4 实验验证

将对2台PLC进行数据采集的程序封装成2个类，在主窗体类中创建2 个数据采集类的对象，在上位机中实现2个PLC的数据交互，将MATLAB中求得的双机协调工作空间作为双机协作机器人的干涉空间。通过运动学正解，在上位机中获得机器人末端执行器的位置，运行时双机器人末端x、y坐标变化曲线见图7。由图7 可看出，在75 s 时，2 个机器人的末端坐标分别为（35，-18）和（48，-20），1号机器人的末端先于2 号机器人末端进入干涉空间，此时，上位机执行轴暂停命令，使2号机器人停止当前运动并减速停止；在115 s时，2个机器人的末端坐标分别为（35，-18）和（48，-20），1号机器人离开干涉空间，上位机执行轴启动命令，使2 号机器人继续运行。同理，当2号机器人先进入干涉空间时，暂停1号机器人运动。图7中双SCARA机器人移动轨迹变化平缓，可在干涉区间内进行避让，没有发生碰撞，说明控制系统设计合理，运行可靠。

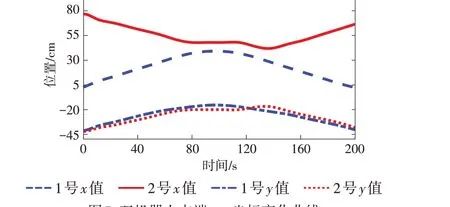
图7 双机器人末端x、y坐标变化曲线

3 结论

建立了双SCARA 机器人运动学模型，推导其正逆解，运用蒙特卡罗法求出了双机器人协作空间。编写了PLC 控制程序，开发上位机控制软件，根据干涉空间范围设计了双机器人避让策略，实现了双机器人的有效避让，运行可靠。