基于模型分析方法的DC-DC变换器设计

张磊，江学焕

（湖北汽车工业学院 电气与信息工程学院，湖北 十堰 442002）

移相全桥变换器利用寄生电容和谐振电感实现零电压开关减小开关损耗，效率超过95%，在电动车充电领域得到广泛应用。众多学者对移相全桥变换器的设计方法进行了研究。周永航［1］在以移相全桥变换器实例基础上使用频率特性分析方法从3个不同方面对系统稳定性分析,但是没有从补偿网络的角度分析系统稳定性。揭贵生等［2］分析了系统传递函数，并用MATLAB 搭建电路电压电流双闭环控制系统仿真模型，通过Simulink工具箱设计了闭环控制网络参数，并在系统仿真模型上验证；王凡等［3-4］设计了电压环补偿网络，在模型中验证了补偿网络的正确性，这些文献中都设计了补偿网络，但是没有结合电路实验验证。宋克岭等［5-7］分别使用了移相式脉宽调制控制芯片UC3875 和UCC3895 设计了移相全桥电源，使用光耦、运算放大器等元件制作了外围反馈回路，使用双闭环控制方式使电路满足了系统的快速响应和稳定性的要求，但是由于采用的是传统的移相控制专用集成芯片，电路的控制精度和灵活性受到限制。上述研究在设计方法、设计过程以及结论验证方面都有一定的局限性。闭环直流变换器是自动控制系统，设计闭环控制校正环节是变换器设计中重要的环节，而控制环节的设计和电路的拓扑与参数有较大的关系［8］。文中提出的基于模型分析方法设计的直流变换器，以MATLAB 作为辅助工具可以简化变换器设计过程，提高效率。

1 移相全桥变换器结构与数学模型

双闭环移相全桥变换器控制见图1。S1～S4是4 个MOSFET，其中S1和S2构成超前桥臂，S3和S4构成滞后桥臂。PWM1～PWM4是对应的驱动波形。Lr为谐振电感，Tr为带中心抽头的高频变压器，VD1和VD2为整流二极管，RL为负载电阻，Rs、R1和R2分别为电流采样电阻和输出电压分压电阻。为避免同一桥臂的2 个开关管同时导通，每个桥臂的2个开关管成180°互补导通，且驱动波形中添加死区时间。每个开关管有固定的导通时间，2个桥臂之间导通角相差1个移相角，通过调节移相角大小控制PWM 占空比，控制输出电压大小。移相全桥变换器电路结构简单，易实现高频化和软开关。

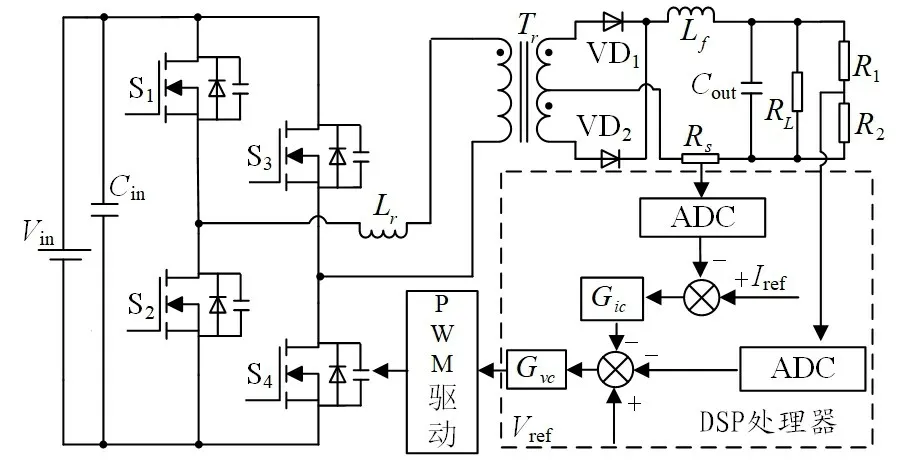
图1 移相全桥变换器闭环控制结构

移相全桥变换器是衍生的Buck 变换器，但移相全桥变换器的高频变压器初级存在漏感导致变压器副边出现占空比丢失的现象，因此可以从Buck变换器小信号模型导出移相全桥变换器小信号模型。移相全桥变换器电压传递函数Gvd(s)、电流传递函Gid(s)数和功率级传递函数Rd［9］分别为

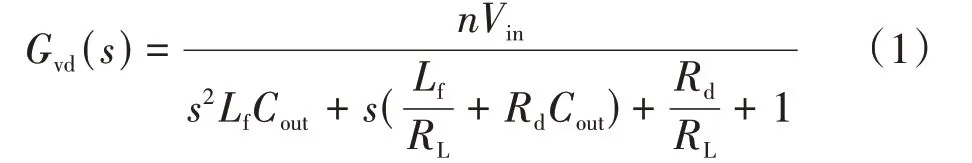
式中：Vin为移相全桥变换器输入电压，取26 V；n为变压器匝比，取4/3；Lr为谐振电感，取1.2 μH；fs为开关频率，取50 kHz；Lf为滤波电感，取107 μH；Cout为滤波电容，取330 μF；RL为负载电阻，取3.2 Ω。

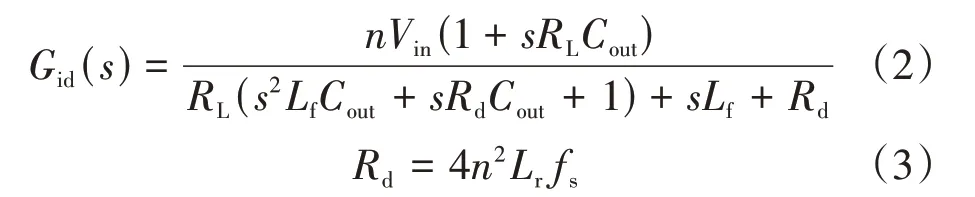
2 系统特性分析与补偿环节设计

2.1 电压环

1）开环特性分析 将变换器各参数代入式（1），得到电压环开环传递函数：

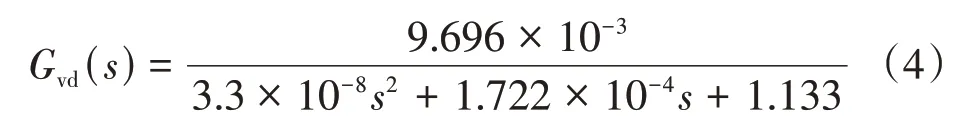
开环Bode图如图2a所示，从图2a中可知增益裕量Gm为-1.2 dB，相角裕量Pm为88.8°，截止频率ωc为5.68× 103rad·s-1。未调节的电压环单位阶跃响应曲线如图2b所示。此时的超调量δ为22.4，上升时间tr为0.27 ms，峰值时间tp为0.61 ms、调节时间ts为1.49 ms，稳态值vt为0.867。

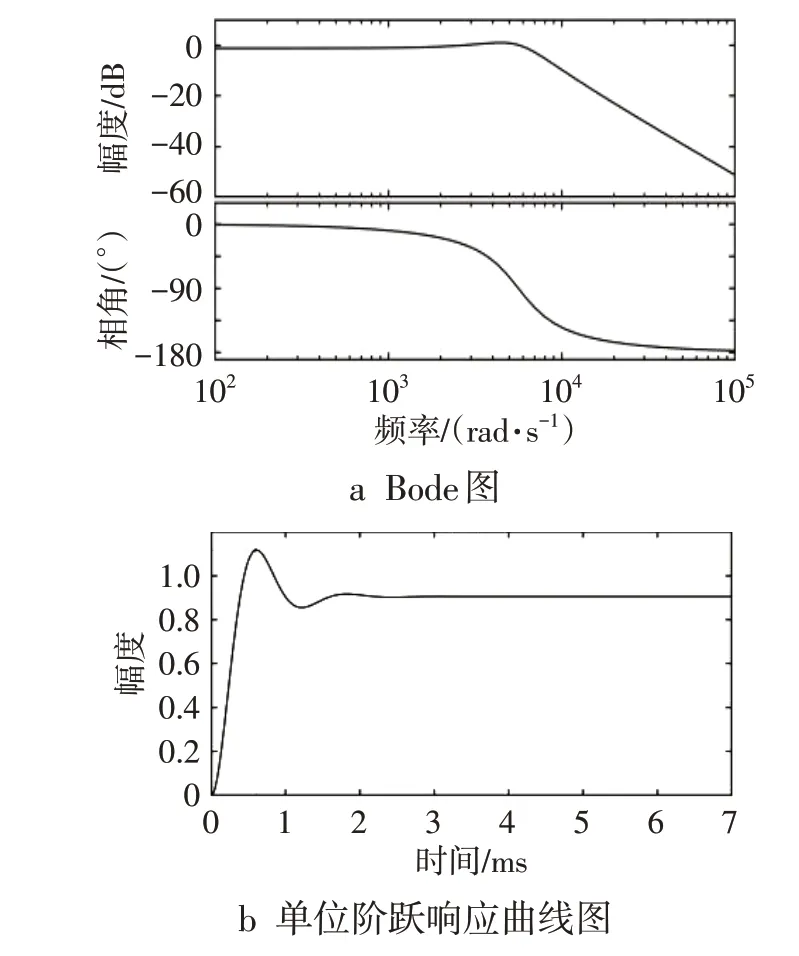
图2 调节前电压环开环特性分析结果图

2）补偿网络环节设计 在设计控制系统时既要提高系统的响应速度，也要增强系统的稳定性。调节后的电压环应具有较大的低频增益和高频段的衰减速度，较小的超调量和稳态误差。文中借助MATLAB 的分析工具SISOTOOL 在根轨迹曲线中添加3 个极点和2 个零点，在SISOTOOL 分析界面拖动极点或者零点位置，观察幅频和相频曲线，使其满足要求，得到电压环的补偿网络传递函数为

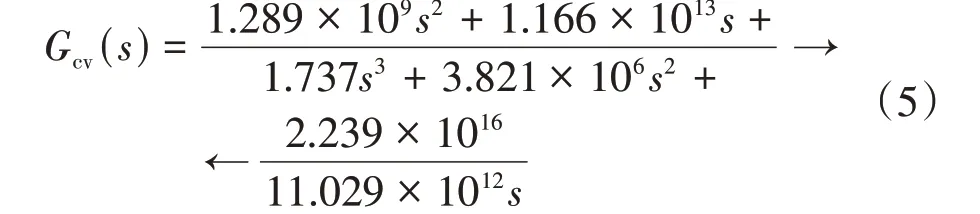
调节之后的电压环系统Bode 图见图3a，此时Gm为36 dB，Pm为75.9°，ωc为3.54 × 104rad·s-1。系统单位阶跃响应曲线见图3b，调节后的系统指标δ为3.51，tr为0.05 ms，tp为0.12 ms、ts为0.9 ms，vt为1。对比图2b 和图3b 可知，系统在调节之后电压环截止频率更大，单位阶跃响应输出超调量更小，稳态值等均满足系统要求。

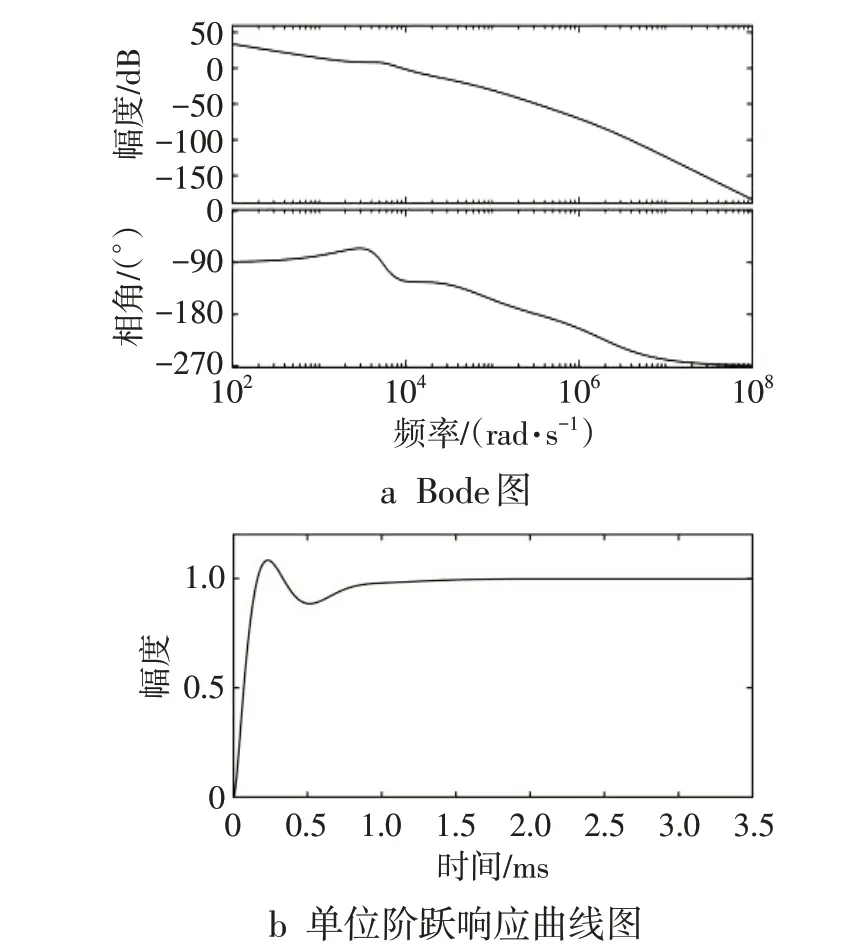
图3 调节后的电压环分析结果图

2.2 电流环

1）开环特性分析 将变换器各参数代入式（2）得到电流环开环传递函数：

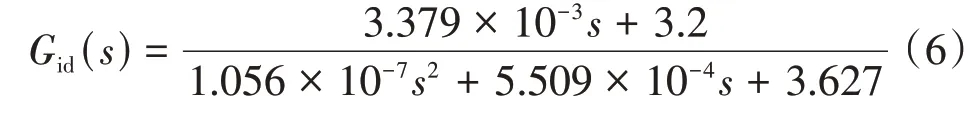
系统Bode图如图4a所示，由图可知Gm为-2 dB，Pm为97.7°，ωc为3.06 × 104rad·s-1。电流环单位阶跃响应曲线如图4b所示，此时δ为346，系统不稳定，选择PI 补偿网络调节电流环，提高电流环抗干扰的性能。

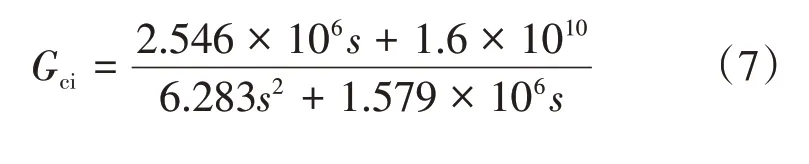
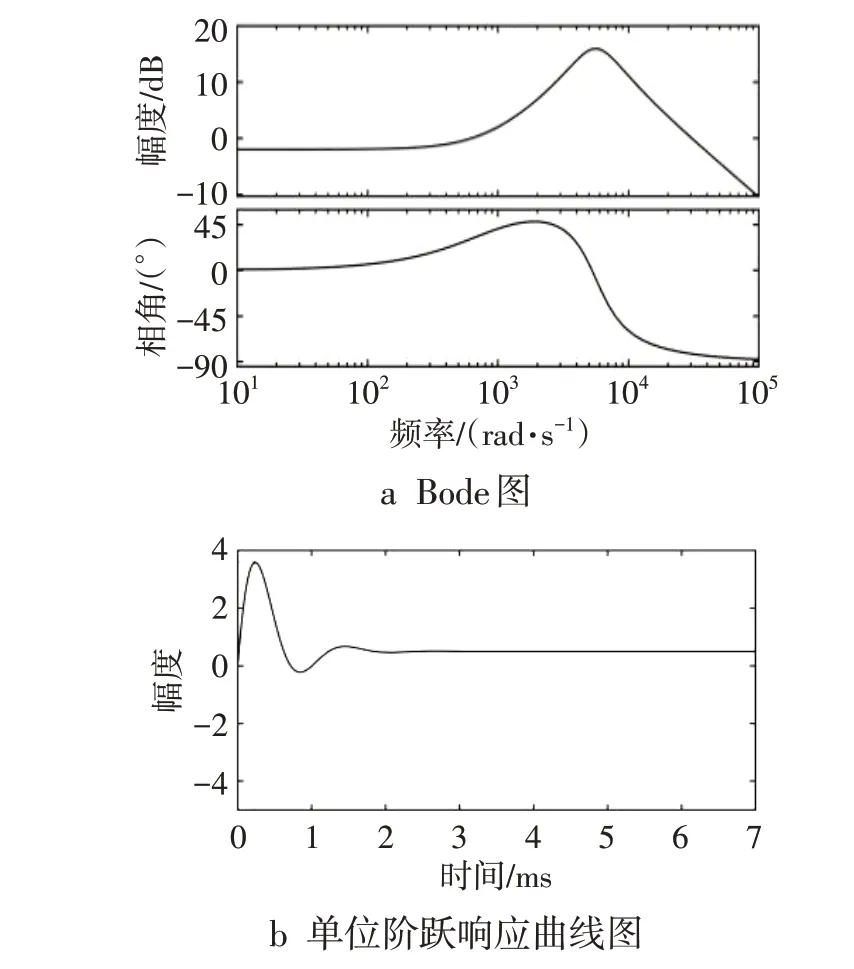
图4 未调节的电流环分析结果

2）补偿网络环节设计 在SISOTOOL 分析工具中通过在根轨迹上添加1个零点和2个极点，经过调节零极点位置得到合适的PI补偿网络。电流环PI补偿网络传递函数为调节后的电流环闭环Bode 图见图5a，此时系统低频增益较大，Pm为76.5°，ωc为4.82 × 104rad·s-1。单位阶跃响应曲线如图5b 所示，电流环低频段增益较大，高频段衰减快，输出无超调量，在频域和时域均满足系统要求。

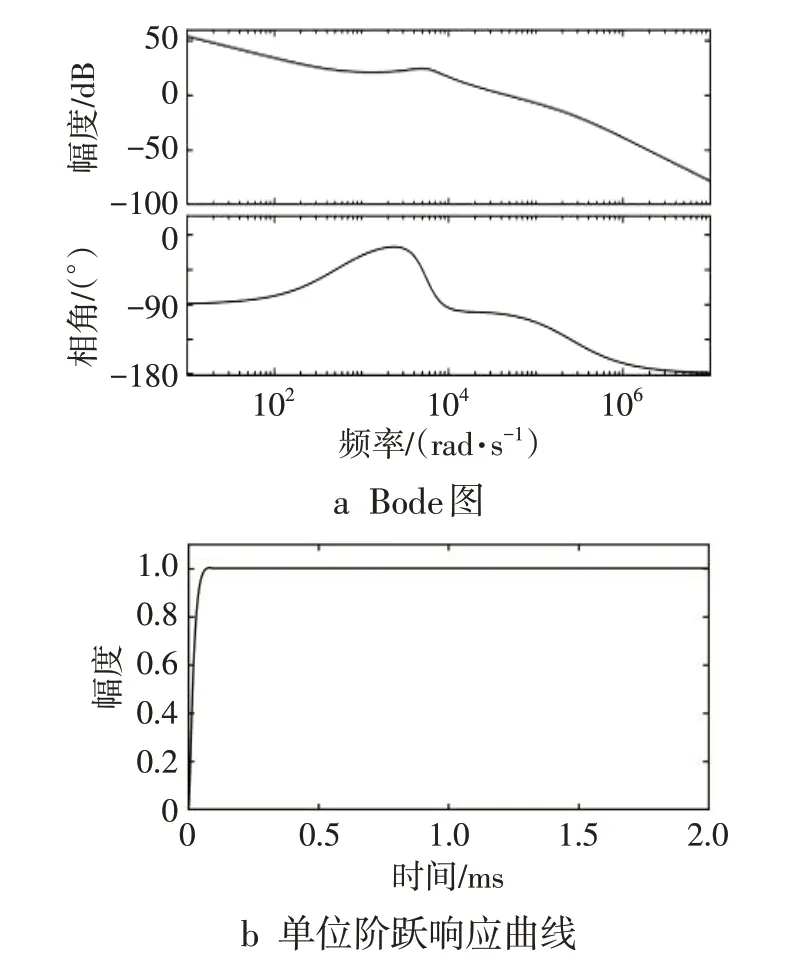
图5 调节后电流环分析结果

3 系统仿真

3.1 闭环控制环路设计

闭环控制框图见图6a，Kv为电压环反馈环节，Ki为电流环反馈环节，Gpv为移相全桥变换器功率环节。为了便于验证设计的环路补偿网络和移植程序到DSP处理器，选择在MATLAB中使用Fcn模块设计控制模型。在Fcn 模块中用户可以自定义函数和开发相应的算法，而且Fcn模块具有较强的程序移植功能。闭环控制程序模型如图6b 所示，Sample 模块采集输出电压和电流数据之后分别输出到电压环VLOOP 和电流环ILOOP 运算，计算出调节量并输入到PWM模块PG产生两路PWM驱动波形，再通过反相器生成对应互补的驱动波形。

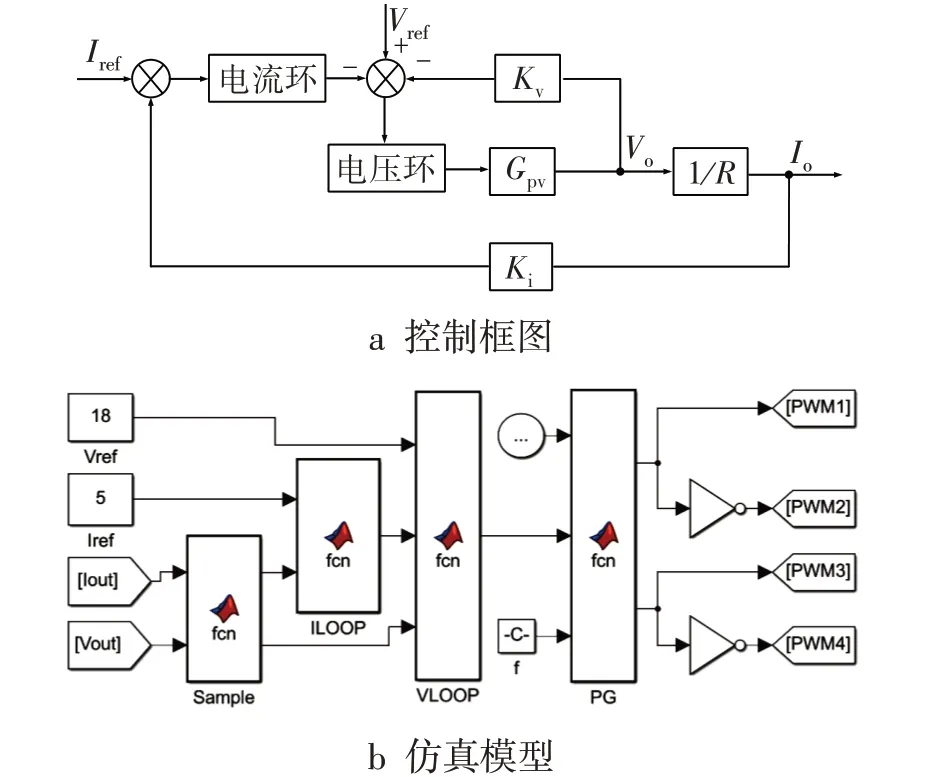
图6 闭环控制设计图

3.2 仿真分析

按照电路的实际参数搭建移相全桥变换器的模型见图7。电路仿真模拟主频为60 MHz 的DSP28034 处理器，运行周期为16.667 ns。RL0、Ideal Switch 和Stair Generator 模块组成了负载切换装置。结合数字式闭环控制环路和主电路模型进行仿真，仿真时间为0.2 s，并在Stair Generator 中设置时间分别为0.04 s、0.14 s 时刻闭合，0.06 s 和0.16 s 时刻断开。在时间节点切换负载得到系统的仿真模型电流和电压输出曲线图8所示。从图8可看出，系统启动之后电压在0.02 s内达到了系统的稳态期望值，在2 次切换负载后都在0.01 s 内恢复稳态值，闭环控制程序达到了良好的控制效果。

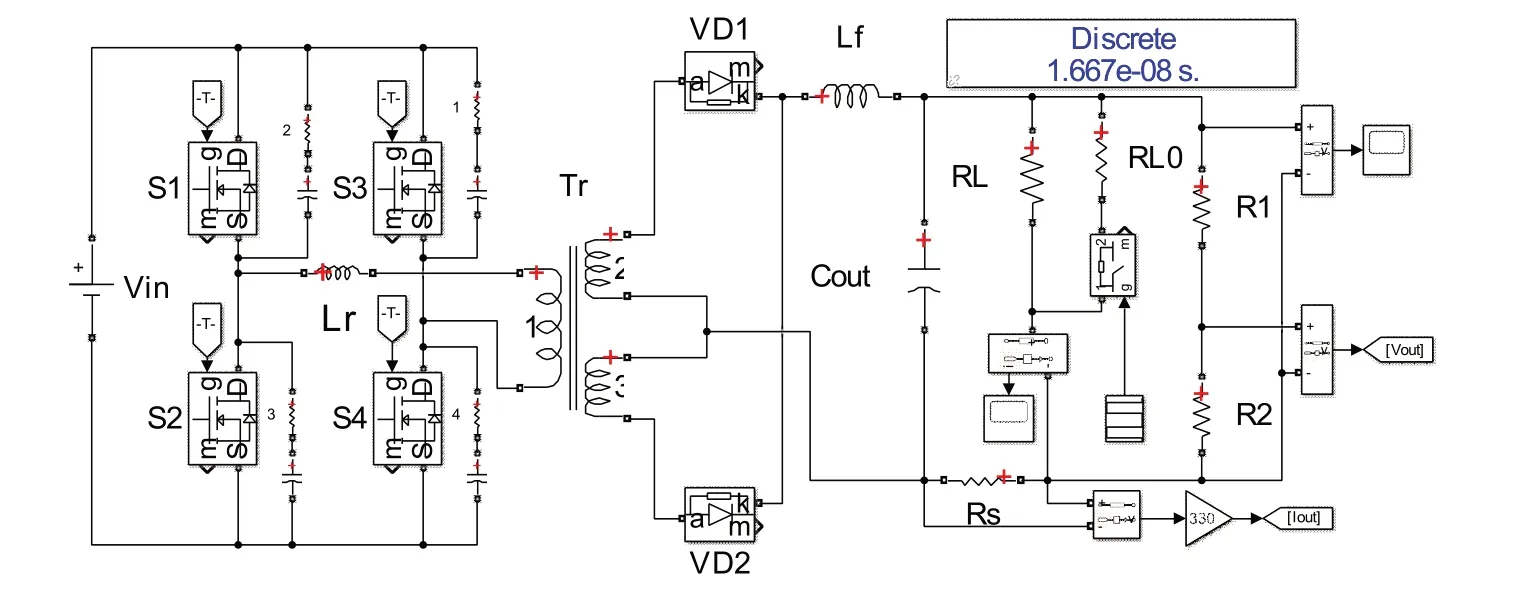
图7 移相全桥变换器电路仿真图

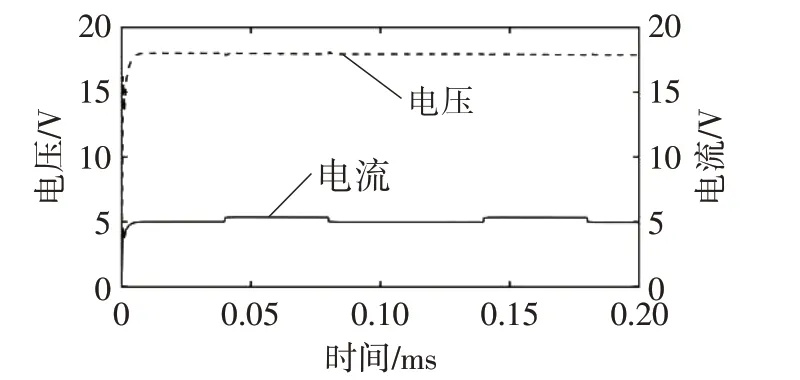
图8 系统仿真曲线图

4 实验分析

供电电源采用两路单通道输出26 V、最大电流3.5 A 的电源并联，使用直流可编程电子负载IT8830B 作为测试负载。移相全桥变换器的开关管S1和S4的PWM 驱动波形见图9a。移相全桥变换器的负载由24 Ω不等间距顺序切换至3.2 Ω，将变换器在全负载范围内进行测试，负载切换局部波形如图9b 所示，导出电子负载数据如图10 所示。综合图9b和图10可知变换器在全范围负载测试情况下，由仿真模型中生成的闭环控制程序可以在电路中较快地调节变换器的输出，随着负载改变，主回路中的电流随之改变，但是输出电压在短暂的过冲之后恢复到设定值，控制效果满足系统的要求。

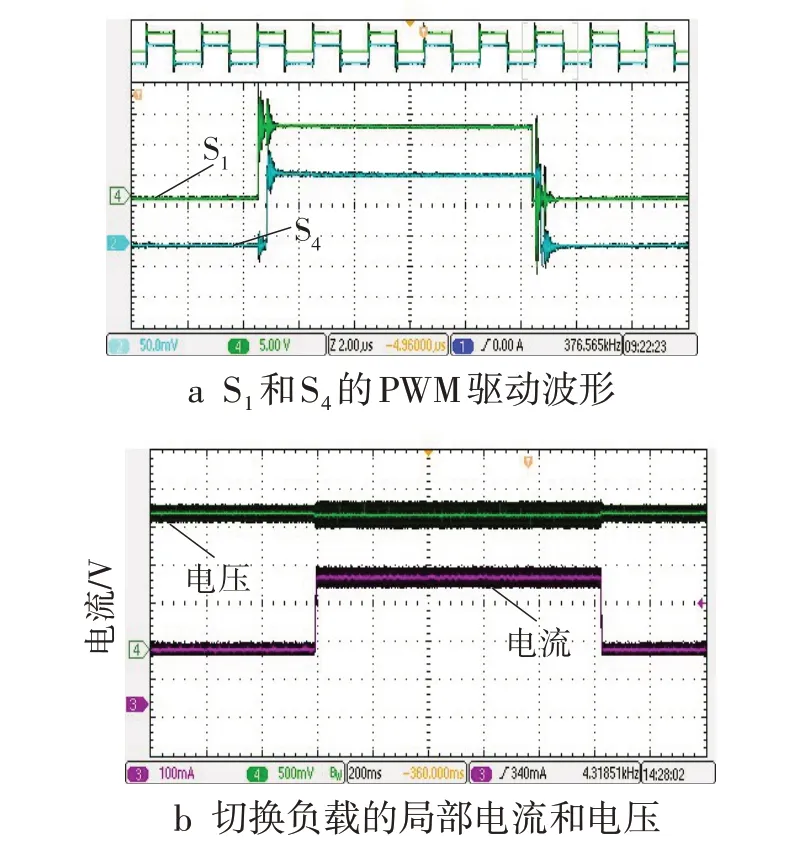
图9 实验测试波形图

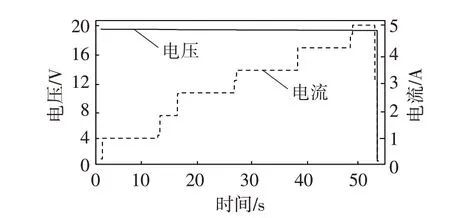
图10 变换器负载数据曲线图

5 结论

文中通过对移相全桥变换器模型分析，设计补偿网络和仿真，结合电路对控制算法进行了验证。基于模型分析设计方法在设计过程中提高了变换器设计效率，降低了补偿器设计复杂度，实现了DC-DC变换器良好的控制效果。后续可优化高频变压器设计，降低变压器的漏感，缓解副边占空比丢失带来的影响，同时对闭环PID 参数优化，进一步提高系统的动态响应和降低稳态误差。