商用车驾驶室半主动悬置的建模仿真

李楚琳，田晨，杨朝阳，曹坤泽，袁显举，陈小兵

（湖北汽车工业学院 汽车工程学院，湖北 十堰 442002）

商用车行驶工况具有时间长、距离远、路况多变的特点，人们对商用车驾驶室的舒适性要求日益增高，而驾驶室悬置是提高舒适性的重要零部件。为降低驾驶室振动，目前国内外研究大多对汽车驾驶室四点悬置系统中结构参数进行精确匹配及优化结构［1-3］，具有一定的局限性。当车辆行驶条件变化时，悬置系统结构参数不可调，驾驶室舒适性无法达到预期改善效果。半主动控制能根据车辆不同行驶条件下的实时激励产生实时控制力，形成闭环反馈。驾驶室动力学模型是半主动控制研究的基础，目前商用车驾驶室舒适性的模型大致分为2种：1）商用车1/2模型［4-5］，主要考虑驾驶室的垂直运动与俯仰运动，模型简单能反映车辆主要性能，但忽略了侧倾运动；2）商用车整车模型［6］，与实际情况较相符，但模型复杂，需要大量建模参数且各系统会产生误差累积，导致分析驾驶室振动时难以保证精度。此外，有学者提出六自由度驾驶室模型，对驾驶室质心处的垂直振动、俯仰振动及侧倾振动加以控制［7］。文中以商用车驾驶室为研究对象，建立三自由度动力学模型，基于最优控制理论设计控制模型，利用Simulink进行仿真分析。

1 系统动力学模型

1.1 驾驶室动力学模型

对某型商用车驾驶室及悬置系统进行简化，主要考虑驾驶室质心处的垂直振动、侧倾振动及俯仰振动。驾驶室与车体通过4对复合隔振单元连接，由弹簧和外置电磁阀可调阻尼器构成。采用集中质量法建立三自由度驾驶室悬置系统模型，驾驶室质心与坐标系原点重合，X轴平行于地面指向前方，Y轴指向驾驶员左侧，Z轴通过质心指向上方，如图1所示。动力学方程为

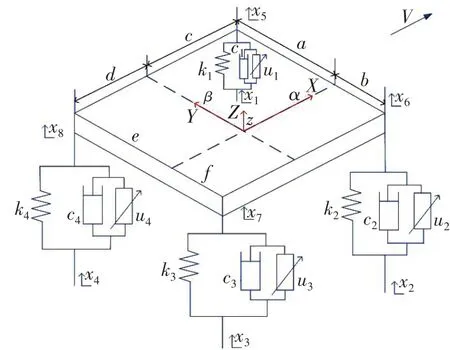
图1 三自由度驾驶室悬置系统模型

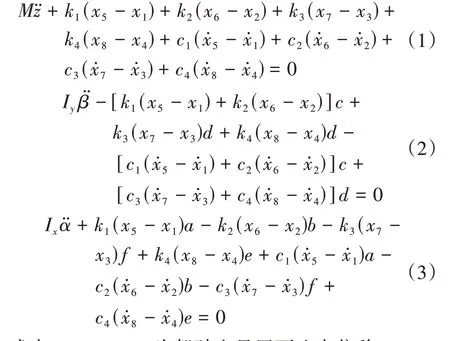
式中：x1、x2、x3、x4为驾驶室悬置下止点位移，x5、x6、x7、x8为驾驶室悬置上止点位移；M为驾驶室质量；Ix、Iy分别为驾驶室在侧倾与俯仰方向的转动惯量；k1、k2、k3、k4为驾驶室悬置中弹簧刚度；c1、c2、c3、c4为驾驶悬置中阻尼器阻尼；a、b、c、d、e、f分别为左前、右前、右后、左后端驾驶室悬置上支撑点至驾驶室质心的距离。U1、U2、U3、U4为驾驶室悬置的控制力，即可调阻尼器的阻尼力。

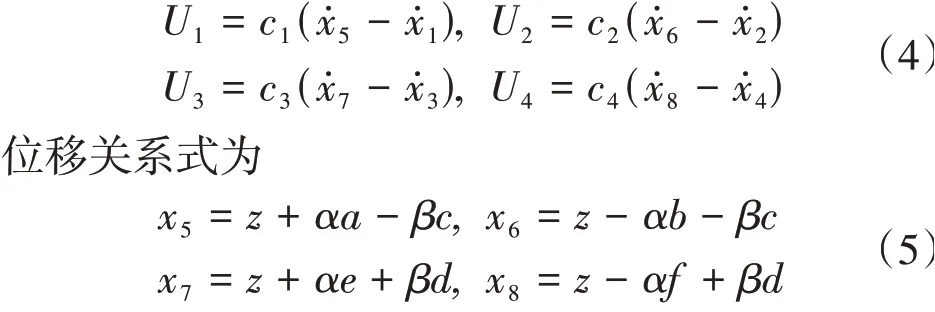
式中：z为驾驶室质心处的垂直位移；α、β分别为绕X轴、Y轴的转动角度。

1.2 驾驶室悬置输入模型

实际工况中，驾驶室悬置系统的激励输入主要来自发动机等内部机体振动和路面外部输入，激励通过驾驶室悬置下止点输入驾驶室悬置系统。由于速度、路面等行驶条件的不规律性，驾驶室悬置的激励输入具有一定的随机性。激励输入模型以路面输入模型为基础，经过一定的衰减，达到路测输入量级［8-9］，满足一定的随机性。路面激励输入模型根据《路面不平度表示方法草案》，采用滤波白噪声法［10］模拟，激励方程为

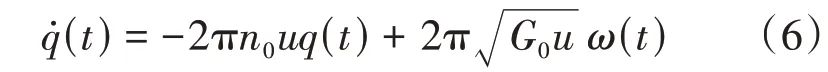
式中：q(t)为时域路面随机位移；ω(t)为高斯分布白噪声；n0为下截止空间频率，取0.01 m-1；u为车速。G0为仿真B 级公路路面不平度系数，取6.4×10-5m3。驾驶室后悬置的激励输入相对前悬置有一定的滞后时间：

2 控制策略设计

2.1 整体方案

商用车驾驶室半主动悬置控制系统通过改变阻尼器外置电磁阀的电流大小，改变阻尼器的阻尼特性，从而改变振动传递特性，抑制驾驶室质心处的振动，达到提高驾驶室舒适性的目的。控制原理如图2 所示。控制系统由驾驶室模型和最优控制器构成。当商用车行驶时，产生实时可变的外部激励，经过信号处理进入最优控制器，控制器利用最优算法计算得到实时变化且满足适调值范围的最优控制力。此时根据可调阻尼器特性曲线，利用查表法得到该控制力下的电流，改变电磁阀电流大小，改变阻尼器特性，改变悬置的控制力。前悬置可调阻尼力的适调范围为-4000～2200 N，后悬置可调阻尼力的适调范围为-1750～1150 N。

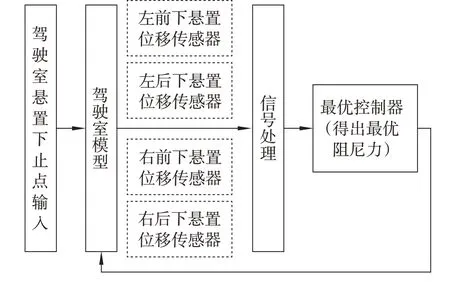
图2 控制系统原理

2.2 最优控制器理论

在三自由度驾驶室模型中，为降低驾驶室质心处的垂直加速度、俯仰加速度、侧倾加速度，使驾驶室在3个方向上达到最优状态，将动力学方程结合位移关系式写成状态方程：

式中：X为状态向量；Y为输出向量；u为控制向量；w为扰动向量；A为系统矩阵；B为控制矩阵；F为扰动矩阵，即路面输入矩阵；C为输出矩阵；D为传递矩阵。

根据汽车平顺性试验方法ISO2631—1：1997（E）中的相关法规可知，各方向的振动对于人体有着不同的影响，驾驶室质心处的侧倾、俯仰、垂直振动会引起横向、纵向、垂向的水平振动，汽车平顺性的评价指标为各轴向加权加速度均方根值和总的加权加速度均方根值。因此以驾驶室质心处垂直加速度、俯仰角加速度和侧倾角加速度的加权平方和最小作为优化目标，尽可能降低驾驶室质心处的振动提高商用车驾驶室的平顺性，即

式中：Q为状态加权矩阵；R为控制加权矩阵；N为Q和R关联的加权矩阵。

根据最优控制理论可知，系统在最优控制律的作用下，从初始状态转移到终端状态满足性能指标最小。系统的最优控制律为

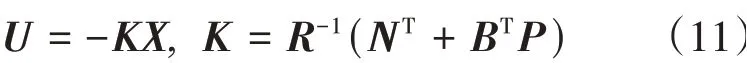
式中：u为驾驶室悬置系统控制力矩阵；K为最优控制反馈增矩阵；P为黎卡提方程解。黎卡提方程为

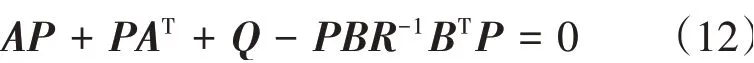
通过MATLAB中LQR函数求解得到实时状态下的K，将K代入式（11）得到最优控制力，作用于悬置处，形成闭环反馈。

3 模型仿真分析

利用Simulink 构建三自由度驾驶室悬置系统模型和LQR 控制器，对汽车在B 级公路上不同车速下的行驶状况进行仿真分析。为客观比较控制器性能，采用某商用车驾驶室相关实测参数（表1）。

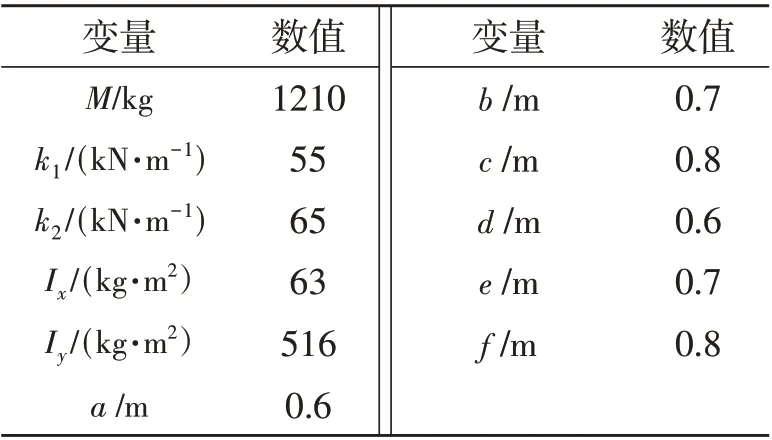
表1 驾驶室悬置主要参数

通过仿真计算可得到：

将K代入Simulink中，将-K与X相乘得到4个悬置系统的控制力，反馈至悬置系统中，构成闭环反馈，得到被动与半主动控制下驾驶室质心处不同轴向加速度的响应结果，如图3所示。由图3可知，基于最优控制的驾驶室悬置系统对比于被动驾驶室悬置系统，在驾驶室质心处的侧倾、俯仰、垂直3个方向上都有较好的控制，减振效果明显。

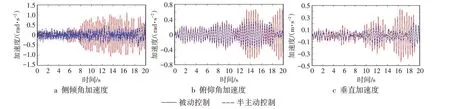
图3 驾驶室质心处加速度仿真结果

对于单轴向连续记录的加速度，通过式（14）计算其加权加速度均方根：

式中：aw(t)为加权加速度变化值；T为作用时间。驾驶室质心处3个方向的加权加速度均方根为

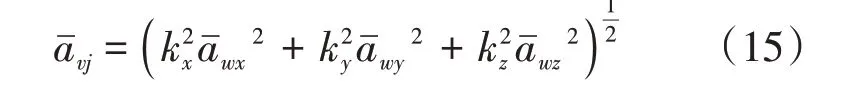
根据式（15）计算得到不同速度下驾驶室质心处不同方向及总加权加速度均方根值，见表2，结果表明：3种不同速度下，采取最优控制后，驾驶室质心处的侧倾角加速度、俯仰角加速度和垂直加速度的均方根值均减小。车速为36 km·h-1时，侧倾角加速度均方根值有较小提高，但俯仰角加速度、垂直加速度以及总加权加速度均方根值均有大幅度减小。车速为72 km·h-1、90 km·h-1时，各项评价指标均有较大减小，驾驶室舒适性有较大提高。

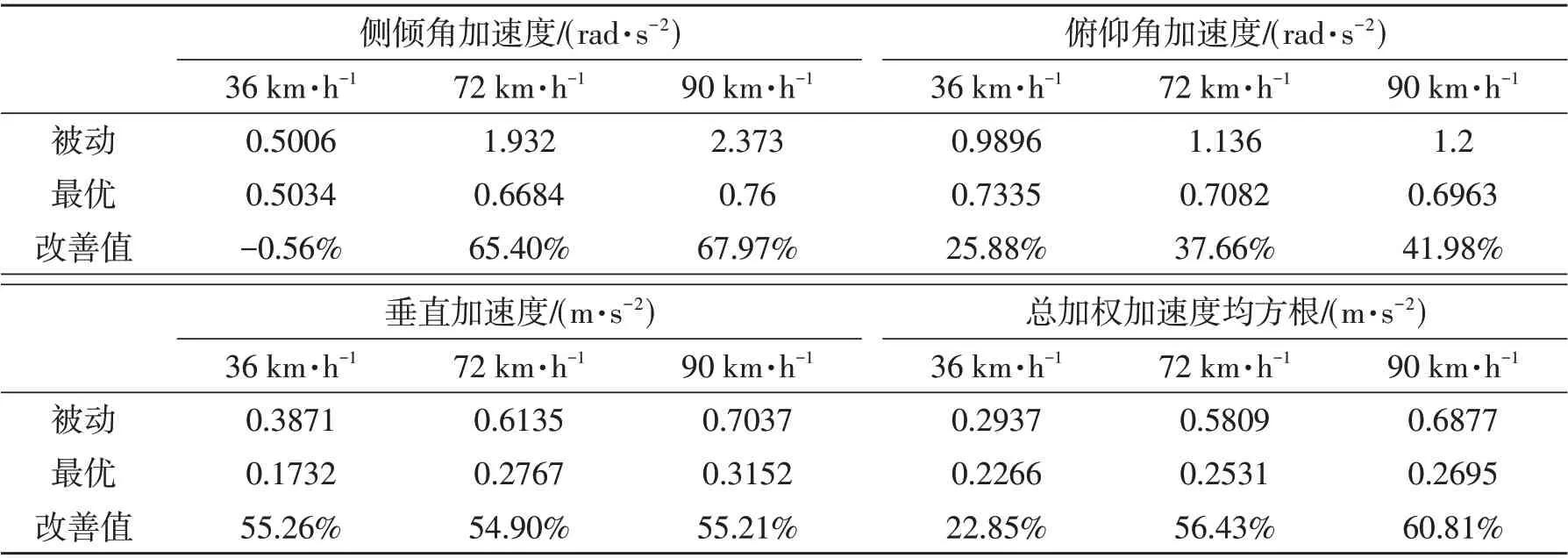
表2 控制评价指标对比分析结果

4 结论

建立三自由度驾驶室悬置系统模型，根据最优控制理论设计最优控制器，在B级路面车速分别为36 km·h-1、72 km·h-1、90 km·h-1的行驶条件下，利用Simulink进行仿真分析，并与被动驾驶室悬置进行比较，结果均表明：采用最优控制器的驾驶室半主动悬置能显著抑制驾驶室质心处侧倾、俯仰及垂直方向上的加速度，对于商用车驾驶室的舒适性有较大改善。