基于Hoek-Brown准则的非常规态型近场动力学弹塑性模型

禹海涛，胡晓锟，李天斌

（1. 成都理工大学地质灾害防治与地质环境保护国家重点实验室，四川 成都 610059；2. 同济大学土木工程防灾国家重点实验室，上海 200092；3. 同济大学土木工程学院，上海 200092）

岩石作为一种天然介质体，具有显著的弹塑性变形特征和断裂力学行为，如何构建一个能够合理描述岩石弹塑性变形特征和连续-非连续力学行为的数值模型，对于深入研究岩石在复杂荷载条件下的物理力学行为至关重要。

近年来学者们提出了不同类型的岩石本构模型，其中Hoek-Brown（H-B）准则是应用最为广泛、影响最大的岩石强度准则［1］，主要通过对大量的岩石试验数据进行统计分析提出的。相比于Mohr-Coulomb（M-C）准则和Drucker-Prager（D-P）准则，H-B准则能够综合考虑岩块的结构面强度以及岩体结构的影响，Hoek 等［2］建立了与地质强度指数（GSI）相关的参数确定方法，因此可以合理地反映岩石强度的非线性破坏特征。Cundall等［3］建立了基于H-B 准则的岩石弹塑性本构模型，根据应力状态和岩石变形的破坏特点建立了不同的流动法则，并将其应用于FLAC软件中进行实现。由于H-B准则的屈服面存在棱线和尖点，在数值求解中需要进行适当的处理，比如H-B 准则屈服函数尖点处的平滑处理［4］，Clausen 等［5］采用主应力空间的返回映射方法并结合有限元进行弹塑性模拟分析，解决了棱线和尖点难以收敛的问题。

然而，目前H-B 准则的研究主要基于传统连续介质力学框架，比如有限元法、有限差分法，对于岩石断裂破坏等不连续问题的研究较为欠缺。近场动力学（PD）［6］作为一种新的非局部的理论，通过空间积分方程代替传统连续介质力学的偏微分方程，避免了模拟不连续问题时的奇异性，因此非常适合描述岩石等准脆性材料的断裂损伤力学行为。Yu等［7］建立了广义微极近场动力学模型来模拟黏弹性问题，并提出了相应的渐近断裂准则，能够合理表征准脆性材料在不同加载速率下的非线性黏弹性行为与断裂模式。Zhou 等［8］建立了基于Drucker-Prager 准则的常规态型近场动力学模型来研究岩土材料的塑性变形行为，并模拟了岩石介质的裂纹萌生和扩展问题［9］。虽然近场动力学已经应用于弹塑性断裂问题的模拟，但是缺少对岩石弹塑性力学行为的准确描述。此外，由于键型［6］和常规态型近场动力学［10］均缺少与材料对应关系的描述，故难以实现材料弹塑性本构模型的通用表述，而非常规态型近场动力学模型［11］中包含了与连续介质力学相对应的变形梯度张量，便于应用岩石相关的弹塑性本构关系，因此，有必要结合广泛应用的H-B 准则和非常规态型近场动力学模型建立岩石的非局部弹塑性断裂力学模型，以期合理表征岩石弹塑性连续变形特征以及断裂非连续力学行为。

本文提出一种基于H-B强度准则的非常规态型近场动力学弹塑性模型，旨在描述岩石的弹塑性变形连续场特征以及断裂力学不连续场力学行为。通过非局部理论框架下主应力空间的返回映射方法，模拟岩石的弹塑性变形特征，并基于建立的等效塑性应变断裂准则实现复杂荷载条件下岩石弹塑性断裂问题的数值模拟。基于数值模拟结果与有限元和试验数据的对比分析，验证该模型的正确性。

1 非常规态型近场动力学理论框架

近场动力学基于非局部理论的思想，将模型离散为物质点的形式，并认为一个物质点不仅与它邻近点发生相互作用，还会受到整个近场非局部作用区域Hx内其他物质点的影响，且物质点之间相互作用以长程力的形式表征，通过对邻域内积分可得近场动力学的运动方程为［6］

式中：D为弹性刚度矩阵。进而可得第一类Piola-Kirchhoff（P-K）应力张量和柯西应力张量

式中：J为雅可比矩阵行列式的值。根据第一类P-K应力与应变能和变形梯度的关系，得到近场动力学的力态表达式

式中：E为弹性模量；υ为泊松比；h为二维问题的厚度；h1为一维问题的截面面积。

2 基于Hoek-Brown 准则的近场动力学弹塑性模型

2.1 屈服方程

Hoek 和Brown［15］在1980 年通过对大量试验进行分析得到了H-B准则，1992年Hoek等［16］对H-B准则进行改进，提出了适用更广泛的广义H-B准则，为

式中：σ1、σ3分别为最大和最小主应力（以拉应力为正）；σc为岩石的单轴抗压强度；a为经验参数，反映材料的非线性程度；mb为经验参数，是岩石的材料常数，表示岩石软硬程度；s为经验参数，与岩体的完整性有关，当岩体完整性较好时，s取1.0。Hoek等［2］还建立了这3个经验参数与地质强度指标（GSI）之间的联系

式中：mi为不同岩体的经验参数；D为爆破影响和应力释放对节理岩体扰动程度的参数，取值范围0～1，当岩体没有受到外界扰动影响时，D=0。

考虑主应力之间大小的关系，基于广义H-B 准则的屈服函数在主应力空间可以表示为

为了在NOSBPD 中建立基于H-B 准则的弹塑性本构模型，通过式（6）求解柯西应力张量，然后基于柯西应力张量的特征矩阵将三维空间下的应力张量转化为主应力张量，从而实现NOSBPD模型中主应力空间的H-B准则的描述。

2.2 主应力空间的塑性流动法则

通过主应力空间能够判断出某点应力状态在屈服面上的位置关系，如单一屈服面、双屈服面相交的棱线或者多屈服面相交的尖点处，如图1所示，若应力状态在σ1=σ2棱线上时，塑性应变的流动需要考虑左右2个屈服面的流动方向ra和rb。

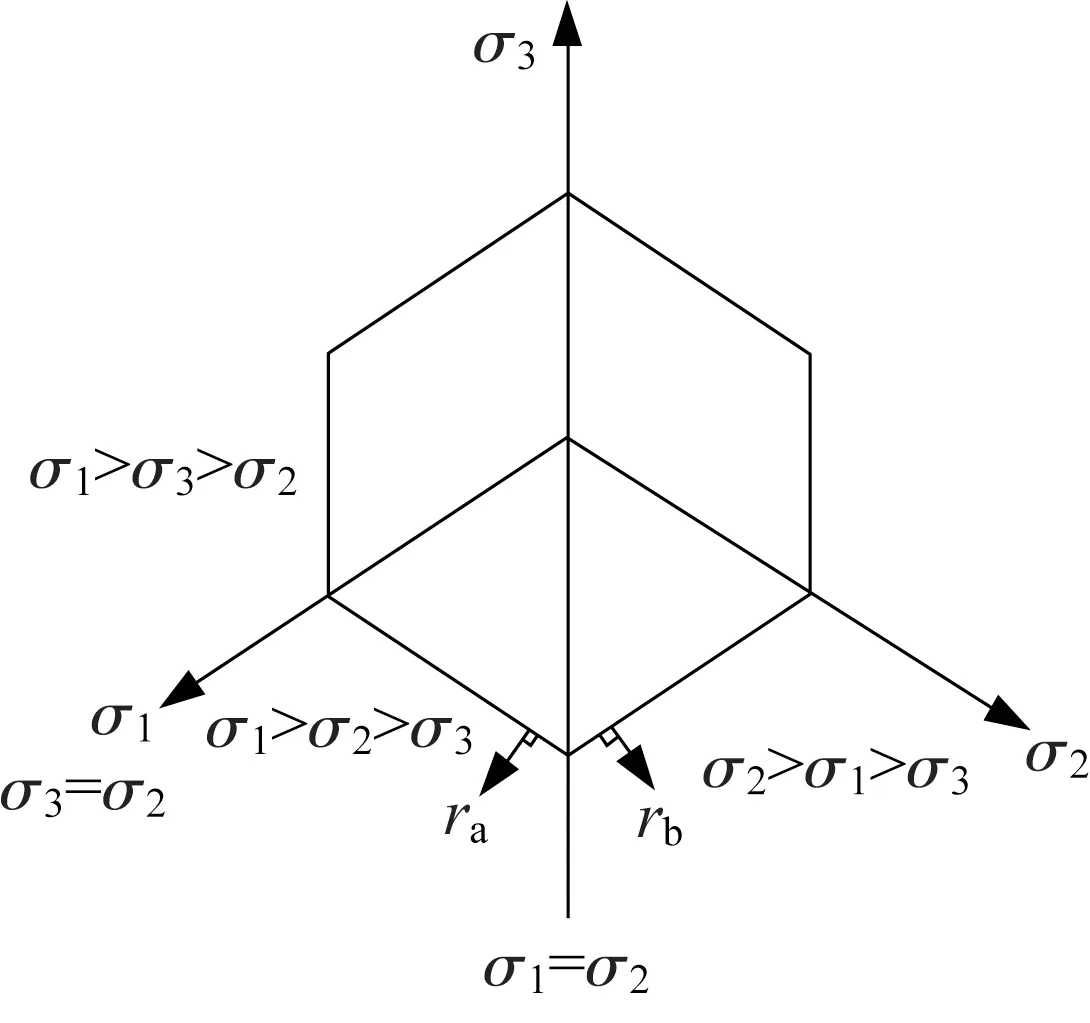
图1 屈服面在π平面的投影Fig.1 Projection of yield surface on π plane

采用相关联流动法则，塑性势函数的形式与屈服函数一致，则塑性应变张量的增量表达式为

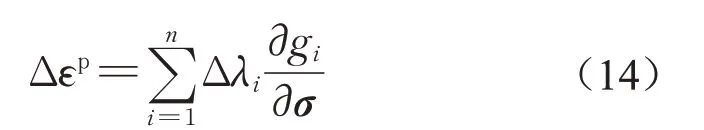
式中：n为式（13）中屈服函数大于零的个数，当应力在屈服面、棱线和尖点时，分别需要1个、2个或多个Δλ，其中λ为塑性因子；gi为屈服函数；σ为主应力张量。当σ1＞σ2＞σ3时，主应变和主应力的塑性增量为

2.3 应力更新

当岩石进入屈服产生塑性应变时，采用主应力空间的返回映射方法计算塑性应变增量，使得更新后的应力落在屈服面上，可得主应力与塑性应变增量表达的非线性方程组为

由于在返回映射的过程中剪应力始终为零，且主应力方向不变，因此可依据之前求解的主应力特征矩阵将满足屈服函数的主应力张量转化为三维空间的应力张量σe，进而得到基于H-B 强度准则的非常规态型力态表达式为

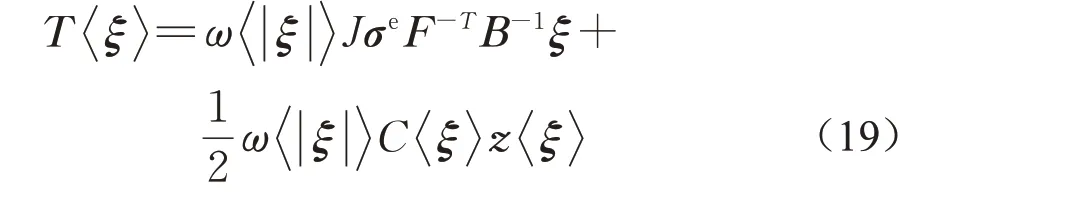
将力态方程（19）代入式（1）即可求解运动方程。

2.4 断裂准则

为了考虑岩石塑性损伤的影响，采用基于等效塑性应变的断裂准则。等效塑性应变的表达式为

2.5 数值求解方法

为了求解NOSBPD运动方程，将模型离散为物质点的形式，位移边界条件通过施加在边界处的虚拟物质点进行实现，即通过边界的虚拟物质点带动内部物质点进行传递，力边界条件可直接将外力转化为体力施加在边界处的物质点上。

基于物质点的控制方程，采用显式的动态松弛方法，即通过增加阻尼项来求解准静态问题［17］，如式（23）：

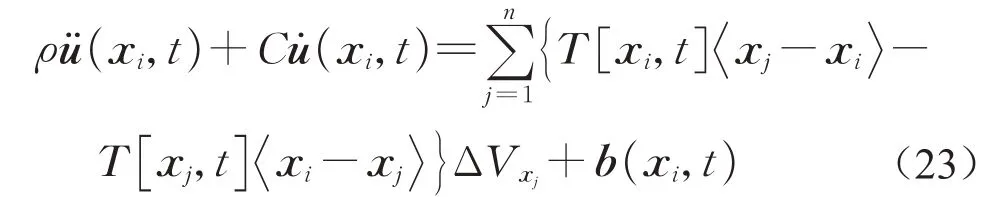
式中：C为人工阻尼。

然后，采用中心差分方法求解位移场u，具体的计算流程如图2所示。

图2 数值求解流程Fig.2 Computational flowchart of the model proposed

3 算例验证

3.1 岩石试样的压缩模拟

为了验证提出的岩石弹塑性非局部力学模型，基于平面应变假设，分别对边长为1 m 的岩块和含孔洞岩块进行模拟分析，并结合有限元模拟结果进行对比验证。假设岩石杨氏模量为28 GPa，泊松比为0.2，单轴抗压强度为100 MPa，广义Hoek-Brown准则中的参数s为1，mb为0.5，a为0.5。对不含孔洞的岩石模型施加位移边界条件，对含圆孔的岩石模型施加力边界条件进行模拟，具体模型及边界条件如图3所示。

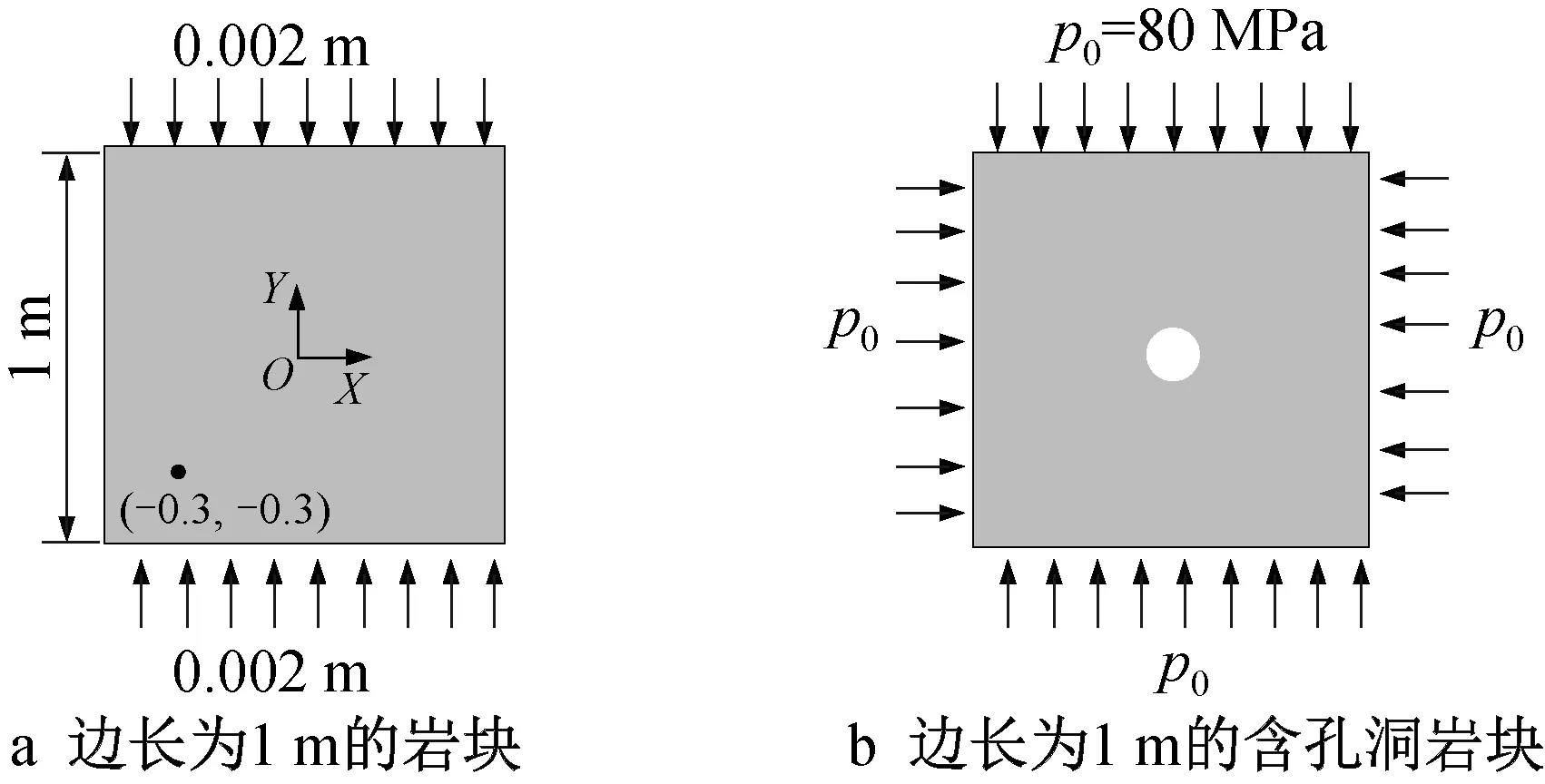
图3 模型及边界条件Fig.3 Model and boundary conditions

对于不含孔洞的模型，将位移加载分为1 000个时间步，对模型上下表面均施加0.002 m 的位移压缩荷载。选择图3中（-0.3，-0.3）为观测点，该点竖直方向的压缩应力与压缩应变响应关系曲线如图4所示。从图中可以看出，当应变接近0.003 5时，岩石进入塑性屈服阶段，本文提出的NOSBPD弹塑性模型计算结果与有限元结果完全一致。

图4 观测点在垂直方向的应力-应变关系Fig.4 Stress-strain relationship of observation points in vertical direction

对于含圆孔岩石的数值模型，为了精确刻画孔洞形状，模型离散为40 090个物质点，物质点间距为0.005 m，对模型四周直接施加80 MPa压力进行计算。图5给出均匀受压荷载作用下含中心圆孔岩石模型的主应力云图和等效塑性应变云图。由图可见，平面模型在四周均布压力作用下，圆孔周边主应力方向为沿径向和环向的圆环形分布，本文NOSBPD模型计算得到的等效塑性应变分布与有限元结果一致，进一步验证了所提出模型的准确性。

图5 主应力及等效塑性应变云图Fig.5 Contours of principal stress and equivalent plastic strain

3.2 含预制裂纹岩石的压缩破坏模拟

岩体中预先存在的缺陷是影响岩石结构稳定性的重要因素，本算例以文献［18］中的受压倾斜缺陷板试验为对象，模拟内部裂纹的萌生与扩展过程。依据文献［18］，试验对象为高0.15 m、宽0.075 m的大理岩模型，其中心处的预制裂纹长0.012 7 m、倾角为30°，模型上下边界分别施加50 MPa 的压缩荷载。大理岩模型的杨氏模量为49 GPa，泊松比为0.19，单轴抗压强度为84.67 MPa，GSI取95，扰动参数D为零，mi为9，通过式（12）可求得广义H-B 准则中的参数s为0.573 8，mb为7.528 2，a为0.500 1，临界等效塑性应变取7.5×10-6。

基于本文NOSBPD 弹塑性模型的计算结果与试验数据对比如图6所示。可见本文模拟的裂纹扩展模式与文献［18］中的试验观测基本一致，即初始的裂纹扩展路径与预制缺陷呈90°夹角，然后随着荷载的增加，产生翼型裂纹。此外，分别采用了11 250个、45 000个物质点离散的数值模型来模拟此问题，得到的裂纹扩展模式均与20 000个物质点离散的数值模型结果图6a一致，验证了本文模型处理弹塑性断裂问题的收敛性。说明本文模型可以有效描述含裂隙岩石在受压荷载下的翼型裂纹扩展问题。

图6 PD预测的裂纹扩展模式与试验结果的对比Fig.6 Comparison of PD-predicted crack growth modes with experimental results

3.3 拱形洞室的模型试验对比分析

Vu 等［19］开展了不同埋深条件下软岩拱形洞室模型的变形破坏试验研究，如图7，其中整体模型尺寸为2.00 m×2.00 m×0.40 m，洞室模型尺寸为0.37 m×0.22 m。软岩模型的密度为2 100 kg·m-3，杨氏模量为0.3 GPa，泊松比为0.32，单轴抗压强度为0.95 MPa，GSI为30，扰动参数D为零，mi为12，mb为0.985，s为4.2×10-4，a为0.522，临界等效塑性应变取8×10-3［20］。限制模型前后表面的移动以模拟平面应变假设，模型底部固定，顶部和两侧压力由单独的液压千斤顶系统控制，通过调整施加的竖向和水平应力可以模拟不同埋深和侧向压力系数。限于篇幅，本文选取侧压力系数为1 的试验数据进行对比分析，即施加于试验模型顶部和两侧压力均相等，且分别考虑3 种围压条件，分别为280 kPa、525 kPa 和700 kPa。

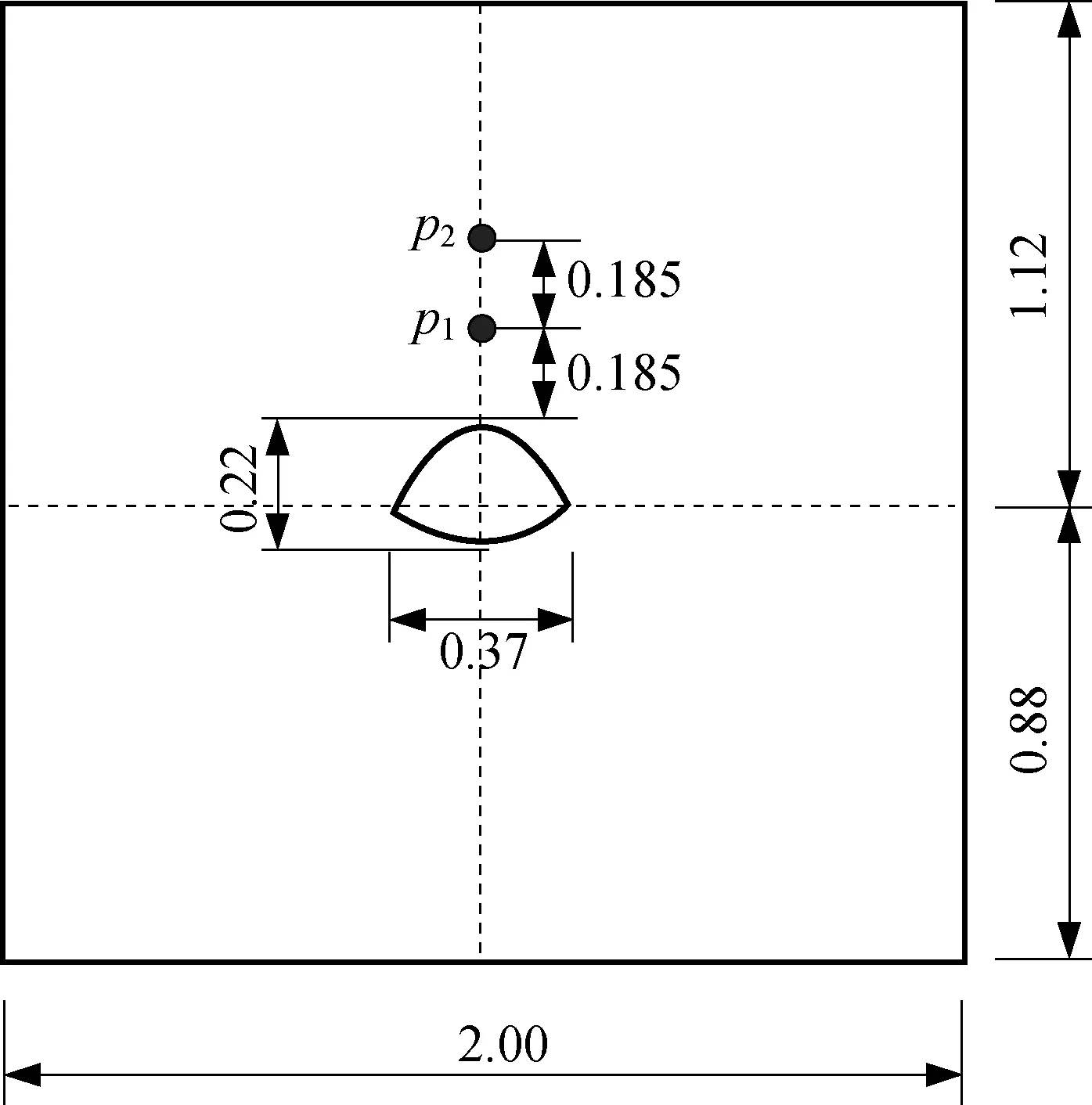
图7 拱形洞室试验示意（单位：m）Fig.7 Sketch of vaulted cave test（unit:m）

图8 为280 kPa 的围压条件下采用本文NOSBPD 模型得到的塑性区分布结果与试验受损情况的对比分析，可见本文模型的塑性预测结果与试验结果吻合较好。图9给出不同围压条件下计算得到的模型结构损伤云图和试验观测结果，可见，围压525 kPa条件下洞室模型基本处于完好状态，而当围压增加至700 kPa 时洞室模型的底部和拱顶发生损伤破坏，整体破坏形态趋向圆形，这与图9c的试验观测现象基本一致，从而进一步说明本文非局部模型用于模拟地下洞室弹塑性损伤分析的有效性。

图8 塑性区域对比Fig.8 Comparison of plastic regions

图9 不同围压条件下的洞室损伤Fig.9 Damage of cavern under different confining pressure conditions

4 结论

提出了一种基于Hoek-Brown（H-B）强度准则的非常规态型近场动力学（NOSBPD）弹塑性模型，可以同时描述岩石的弹塑性变形连续场特征以及断裂力学的非连续场行为，即该模型基于H-B 准则在主应力空间的返回映射方法，能够准确地描述岩石材料的弹塑性变形特征；同时，结合建立的等效塑性应变断裂准则，还可以实现岩石在复杂荷载作用条件下的断裂行为全过程力学分析。基于所提出的NOSBPD弹塑性模型，模拟分析了压缩荷载作用下完整岩石试样与含孔洞岩石试样的弹塑性变形行为，计算结果与有限元结果基本一致，从而验证了本文模型的准确性。通过与试验观测结果对比分析表明，本文模型还可以准确地描述在单轴压缩条件下含预制斜裂纹的岩石试样沿裂尖的翼型裂纹的萌生与扩展过程。此外，还将该模型应用于拱形洞室的弹塑性破坏数值模拟，发现当围压较大时，洞室的拱顶和底部首先发生破坏，分析结果与室内模型试验观测现象基本一致，进一步说明了本文模型用于岩石弹塑性断裂问题模拟的有效性，为实际工程岩石弹塑性破坏的连续-非连续问题研究提供了可靠的分析手段。

作者贡献声明：

禹海涛：项目负责人、论文构思、指导模型构建及数据分析、论文修改。

胡晓锟：模型构建、数据分析及论文撰写。

李天斌：论文修改。