单轴压缩下炭质板岩的应变速率效应及声发射特性

肖颖鸣，乔亚飞，2，李红儒，何满潮

（1. 同济大学土木工程学院，上海 200092；2. 同济大学岩土及地下工程教育部重点实验室，上海 200092）

炭质板岩作为地质构造运动形成的一种特殊软岩，广泛分布于我国西部地区。随着“西部大开发”战略的实施，穿越炭质板岩的隧道工程愈来愈多。这些隧道时常发生大变形灾害，如在建的木寨岭公路隧道［1］。除流变与构造应力的诱发因素外［2-3］，开挖工序及开挖速率也会影响大变形的发展，这与岩石力学特性的应变速率依赖性有关［4］。因此，揭示应变速率对炭质板岩力学特性的影响规律对进一步认识隧道大变形的发生机制和防控具有重要意义。

应变速率会对岩体的基本力学参数、能量演化规律及声发射特征产生影响。刘晓辉等［5］认为准静态应变速率下煤岩存在应变速率临界值；低于临界值时，煤岩的峰值强度、弹性模量等逐渐增加，而高于临界值时逐渐降低；在准静态应变速率内，煤岩的特征应力与峰值应力比值呈减小趋势［6］。李海涛［7］发现煤岩的破坏时间和强度等随加载速率的增大先增加后减小。王晓东等［8］则发现花岗岩的特征应力值随加载速率增大均逐渐增大。杨仕教等［9］指出在一定加载速率内，石灰岩由峰值强度至残余强度之间的跌落曲线随应变速率增加而变陡。尹小涛等［10］分析了应变速率对能量演化机制的影响，认为高应变速率下剧烈的能量变化更容易诱发岩爆灾害。岩石破坏的本质就是微裂纹不断闭合、萌生、演化至最后成核的过程，在该过程中岩石内部的应变能会以弹性波的形式进行释放，产生声发射现象［11-12］。采用声发射监测技术，部分学者分析了应变速率对岩石渐进破坏过程的影响，比如Liu等［11］指出静载作用下大理岩的累计声发射数随应变速率的增加逐渐减小；姜德义等［13］发现在单轴压缩状态下，盐岩的单次声发射信号频率随加载速率增大逐渐增大；杨文君等［14］基于砂岩加载速率与声发射累计振铃计数构建了砂岩的损伤本构。综上可知，应变速率对不同岩石力学特性的影响规律存在差异，需要开展针对性的试验研究。

由于突出的各向异性特征，很多学者研究了层理倾角对炭质板岩力学特性的影响［15-17］，如刘运思等［15］通过7种不同层理倾角下炭质板岩的单轴压缩试验分析了弹性参数及抗压强度随层理倾角的变化规律；王永刚［16］对炭质板岩进行常规三轴试验，认为竖直层理试样横向扩容更早，但水平层理试样体应变增长更迅速；李二强等［17］针对炭质板岩进行了不同层理倾角的巴西劈裂试验。既有关于应变速率对炭质板岩力学特性影响的研究尚少，这不利于炭质板岩隧道开挖过程的精准分析，故亟需开展不同应变速率下炭质板岩的力学试验研究。

因此，开展了4 组准静态应变速率（8.50×10-6s-1、1.70×10-5s-1、1.70×10-4s-1、3.34×10-4s-1）下的单轴压缩试验，并同时进行了声发射信号监测，旨在揭示应变速率对炭质板岩力学特性、能量演化规律、声发射特征的影响。

1 试样及试验方法

1.1 试样加工

试验所用炭质板岩均取自渭武高速公路木寨岭隧道2#斜井，钻取试样均呈水平层理，如图1 所示。该岩样主要为灰色与深灰色互层，且厚度较薄，主要成分为石英及黏土矿物，黏土矿物主要包括伊利石、绿泥石、伊蒙混层以及高岭石。根据《水利水电工程岩石力学规程》（SL 264—2001）［18］对试样进行研磨，以保证试样端面的平整度。为减小加工对炭质板岩原始状态的影响，圆柱试样的直径控制在50±2 mm，高度为100±2 mm。

图1 水平层状炭质板岩试样Fig.1 Samples of horizontal layered carbonaceous slate

1.2 试验设备及方法

试验加载设备为意大利Matest 岩石伺服压力机，最大轴力为3 000kN，可采用荷载、位移等方式控制加载，如图2 所示。声发射装置采用16 通道DS2型声发射仪，并设置声发射门槛值为40dB。为分析应变速率对炭质板岩单轴压缩力学特性的影响，采用位移控制的加载方式，共进行了0.05mm·min-1、0.1mm·min-1、1mm·min-1、2mm·min-14 种加载速率的试验，其对应的应变速率分别为8.50×10-6s-1、1.70×10-5s-1、1.70×10-4s-1、3.34×10-4s-1。为了减小试样离散性的影响，每组应变速率值进行3 次平行试验。在试验过程中，加载过程和声发射监测同步进行，并且所有试验均在室温条件下进行。

图2 炭质板岩加载示意Fig.2 Loading diagram of carbonaceous slate

2 单轴压缩下炭质板岩的应变速率效应

2.1 应变速率对应力-应变曲线的影响

选取4种不同应变速率中的一组平行试验进行分析。图3 为4 种不同应变速率下的应力-应变曲线。不同应变速率下的应力-应变曲线均可分为4个阶段：压密阶段、线弹性阶段、裂纹扩展阶段和峰后阶段。

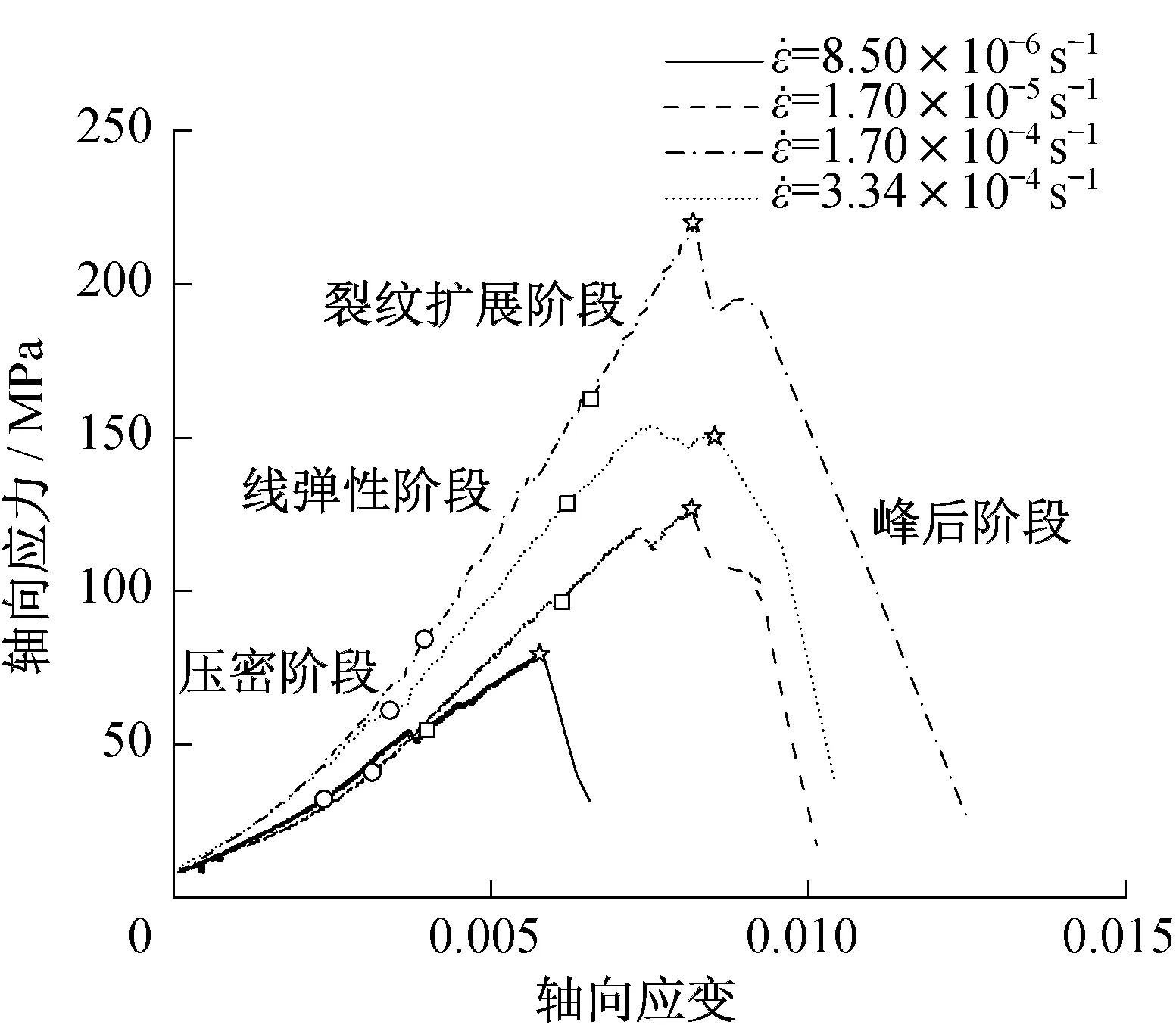
图3 不同应变速率下炭质板岩的轴向应力-轴向应变曲线Fig.3 Axial stress-axial strain curves of carbonaceous slate at different strain rates

2.1.1 压密阶段

压密阶段出现在加载初期，曲线呈上凹型增长。由于试样内部原生裂隙及应变速率的不同，压密阶段范围长短不一。随着应变速率的增加，同等应变下炭质板岩的应力增幅增大，压密阶段的应力-应变曲线随应变速率的增大呈向上方移动趋势（图3）。

2.1.2 线弹性阶段

此阶段，应力-应变曲线呈线性增长。在较低应变速率（8.50×10-6s-1和1.70×10-5s-1）时，试样压缩较慢，出现应力略微下降现象。其原因为在较低应变速率下，炭质板岩微裂隙有较充分的时间发展，微裂隙的形成降低了试样的承载能力。在较高应变速率（1.70×10-4s-1、3.34×10-4s-1）时，炭质板岩内部裂隙没有足够时间发展，试样应力-应变曲线呈较好的线性增长。

采用峰值应力40%～60%区间数据计算试样的弹性模量，统计结果如图4。随应变速率的增大，炭质板岩的弹性模量先增大后减小。应变速率为8.5×10-6s-1、1.7×10-5s-1、1.7×10-4s-1时，平均弹性模量分别为17.96GPa、18.65GPa、27.16GPa，呈现出较好的增长趋势；但当应变速率为3.34×10-4s-1时，平均弹性模量减小为22.33GPa。当应变速率低于1.7×10-4s-1时，随着应变速率的增加，试样内部裂隙快速闭合，短时间内裂隙发展不充分，弹性模量出现增大趋势；在应变速率高于1.7×10-4s-1时，随着应变速率的增大，试样内部结构在较短时间内出现过快调整，试样内部发生多次微破裂，进而导致弹性模量的下降。

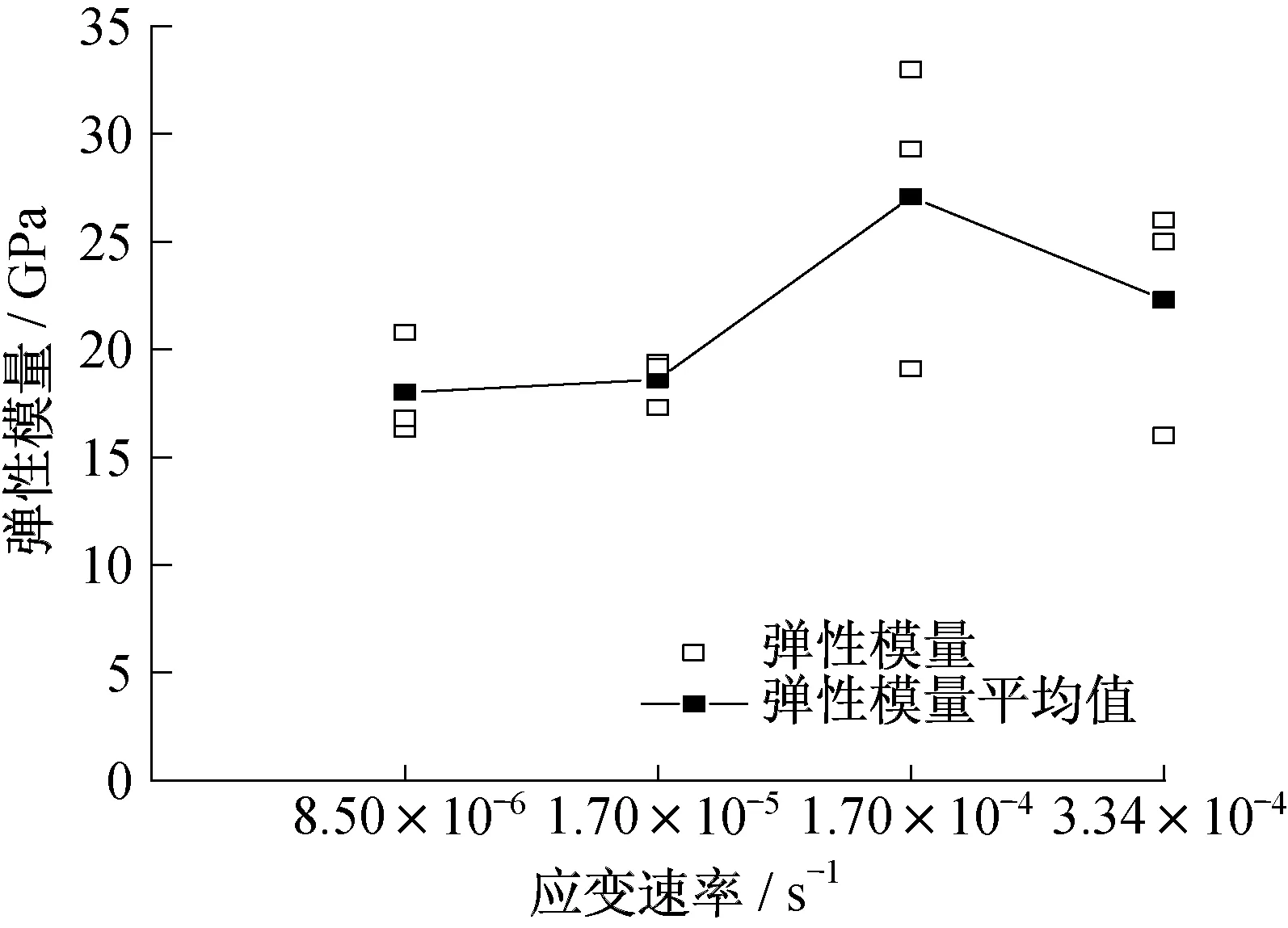
图4 不同应变速率下炭质板岩的弹性模量Fig.4 Elastic modulus of carbonaceous slate at different strain rates

2.1.3 裂纹扩展阶段

此阶段，微裂隙逐渐发育形成宏观裂纹，试样应力-应变曲线偏离线性段，在峰值处发生破坏。图5汇总了不同应变速率下炭质板岩的峰值强度值σf。应变速率对峰值强度的影响规律与其对弹性模量的影响规律一致：当应变速率小于1.7×10-4s-1时，平均峰值强度随应变速率的增加逐渐增大（分别为95.98MPa、121.86MPa、174.55MPa）；当应变速率为3.34×10-4s-1时，平均峰值强度减小为131.44MPa。

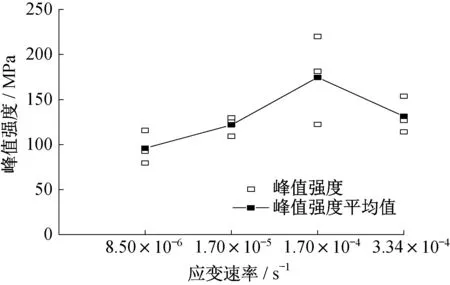
图5 不同应变速率下炭质板岩的峰值强度Fig.5 Peak strength of carbonaceous slate at different strain rates

2.2 应变速率对能量特征曲线的影响

2.2.1 能量分析原理

岩石的变形破坏是岩石内部能量不断演化并与外界交换的结果［19］。荷载作用下岩石的变形破坏过程主要涉及到弹性能、塑性能、损伤能等多种形式能量之间相互转化，但其总能量保持不变［20］。

假设单位体积炭质板岩是一个没有与外界进行热交换的封闭环境，则炭质板岩各部分能量之间关系如式（1）：

式中：U为外力做功所产生的单元总应变能；Ue为可释放的弹性应变能；Ud为耗散应变能。在单轴压缩条件下，仅有轴向压力对炭质板岩做功，因此单位体积内的输入总能量为

式中：σ为轴向应力；ε为轴向应变。假定弹性模量E为定值［21］，则单位体积内的弹性能为

式中：σi为第i次数据采集时的轴向应力。由式（1）-（3）可知，耗散能密度为

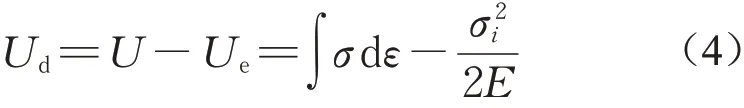
2.2.2 应变速率对总应变能密度的影响

采用式（2）计算不同应变速率下炭质板岩的总应变能密度演变规律，如图6 所示。随着轴向应变的增加，单位体积内试样吸收总能量逐渐增加；在加载初期呈上凹型，这与试样本身的原生孔隙被压密有关，随后近似呈S 形发展。应变速率低于1.7×10-4s-1时，单位体积内输入总能量随应变速率的增大而增大，3种应变速率下的最大总应变能密度分别为2.8×105J·m-3、6.8×105J·m-3、1.4×106J·m-3；在应变速率为3.34×10-4s-1时，单位体积内输入总应变能减小为9.2×105J·m-3。

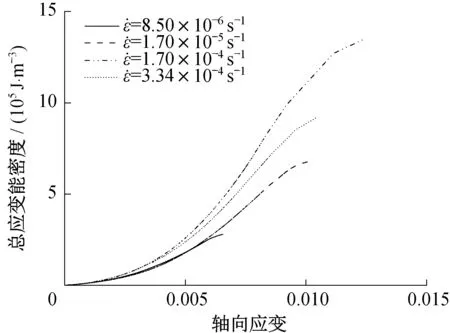
图6 不同应变速率下炭质板岩的总应变能密度与轴向应变关系Fig.6 Axial strain-total strain energy of carbonaceous slate at different strain rates

2.2.3 应变速率对弹性应变能密度的影响

图7对比分析了不同应变率下炭质板岩弹性应变能密度的变化规律。弹性应变能密度在峰值应变前逐渐增加，在峰值应变处达到最大值，后急剧减小。不同应变速率下弹性应变能密度的积聚趋势与应力-应变曲线变化趋势类似。在应变速率小于1.70×10-4s-1时，炭质板岩的弹性应变能密度曲线逐渐上移；大于1.70×10-4s-1时，弹性应变能密度曲线出现了下移。

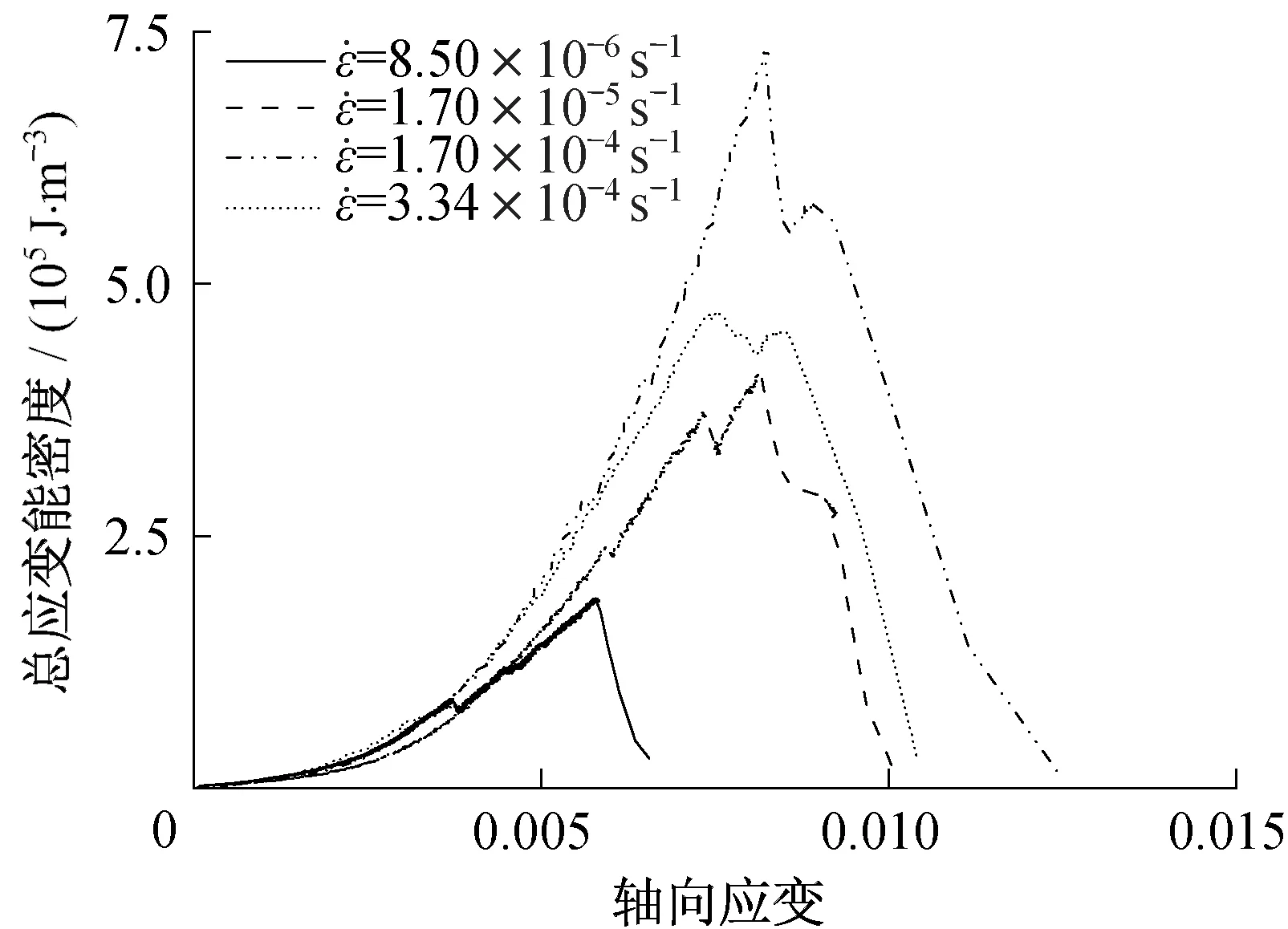
图7 不同应变速率下炭质板岩的弹性应变能密度与轴向应变关系Fig.7 Axial strain-elastic strain energies of carbonaceous slate at different strain rates

2.2.4 应变速率对耗散能密度的影响

图8对比分析了不同应变速率下耗散能密度的演变规律。随着轴向应变的增加，耗散能密度先逐渐增大，后与横坐标近似平行，耗散能密度几乎不产生变化，最后出现急剧增大。当应变速率低于1.7×10-4s-1时，3 种应变速率下的耗散能密度最大值分别为：2.5×105J·m-3、6.7×105J·m-3、1.3×106J·m-3。应变速率为3.34×10-4s-1时，耗散能密度的最大值为8.9×105J·m-3，出现了下降趋势。

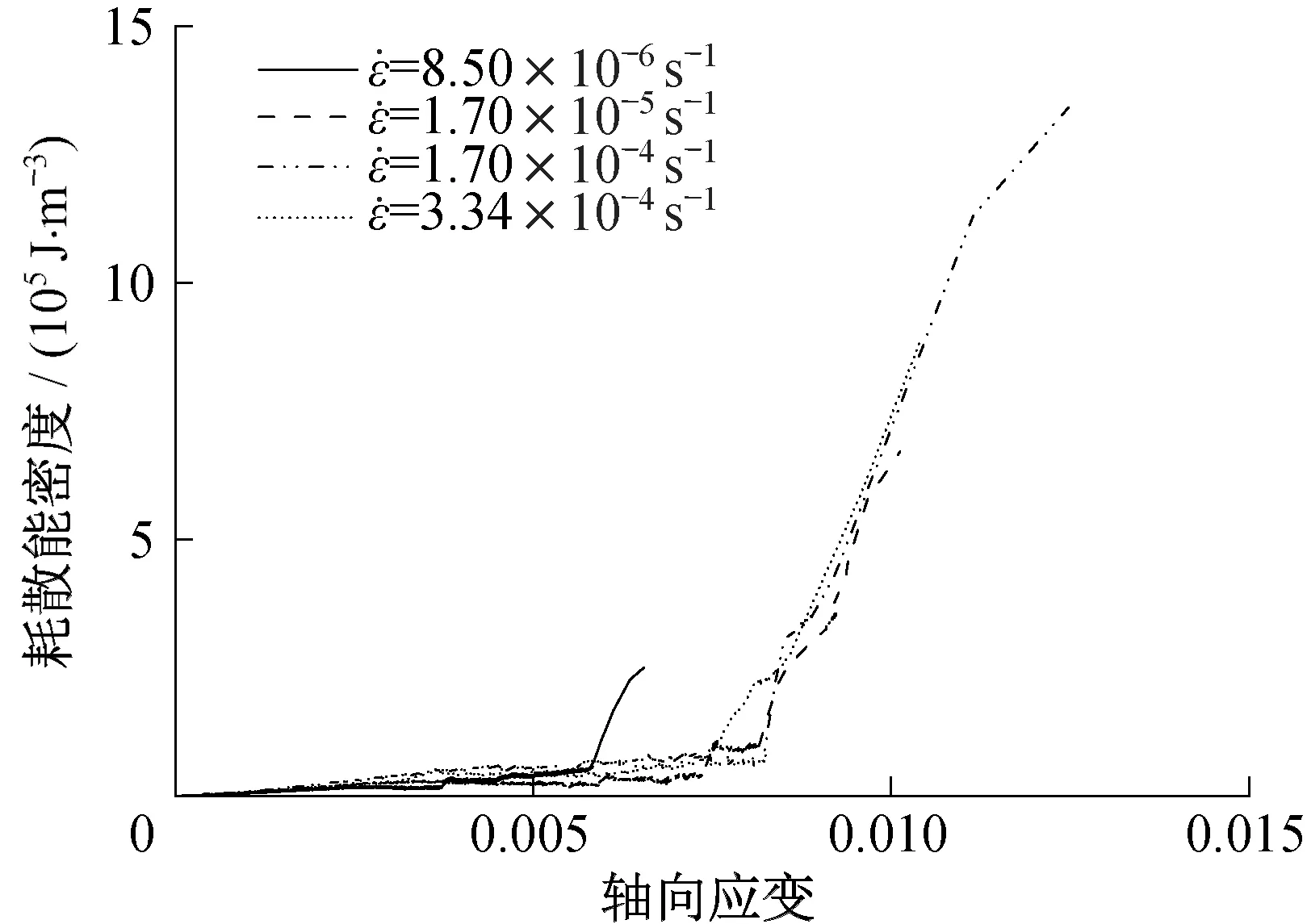
图8 不同应变速率下炭质板岩的耗散能密度与轴向应变Fig.8 Axial strain-dissipated energy of carbonaceous slate at different strain rates

2.3 应变速率声发射信号对振铃计数特征的影响

2.3.1 振铃计数特征

振铃计数是振铃脉冲超过阈值电压的次数，能够反映岩石的损伤程度。图9汇总分析了不同应变速率下加载过程中炭质板岩的振铃计数特征。应变速率为8.5×10-6s-1时，试样内部原生裂纹在加载初始阶段随应力的增大缓慢闭合，此阶段不利于应变能的积聚与释放，故振铃计数处于较低的水平；当应力-应变曲线偏离线性段时，振铃计数信号变得显著，并出现一个较高的声发射计数，且一直处于活跃阶段，直至达到峰值应力。

随着应变速率的增加，振铃计数信号出现于加载初期，如图9d 所示，在压密阶段向线弹性过渡阶段，出现了一定量的振铃计数。过大的加载速率使原生裂纹迅速闭合并相互碰撞挤压，产生大量的声发射信号。而在弹性阶段，振铃计数进入一段平静期。在裂纹扩张阶段，声发射信号再次活跃，大量裂纹开始衍生、扩展成主裂纹。

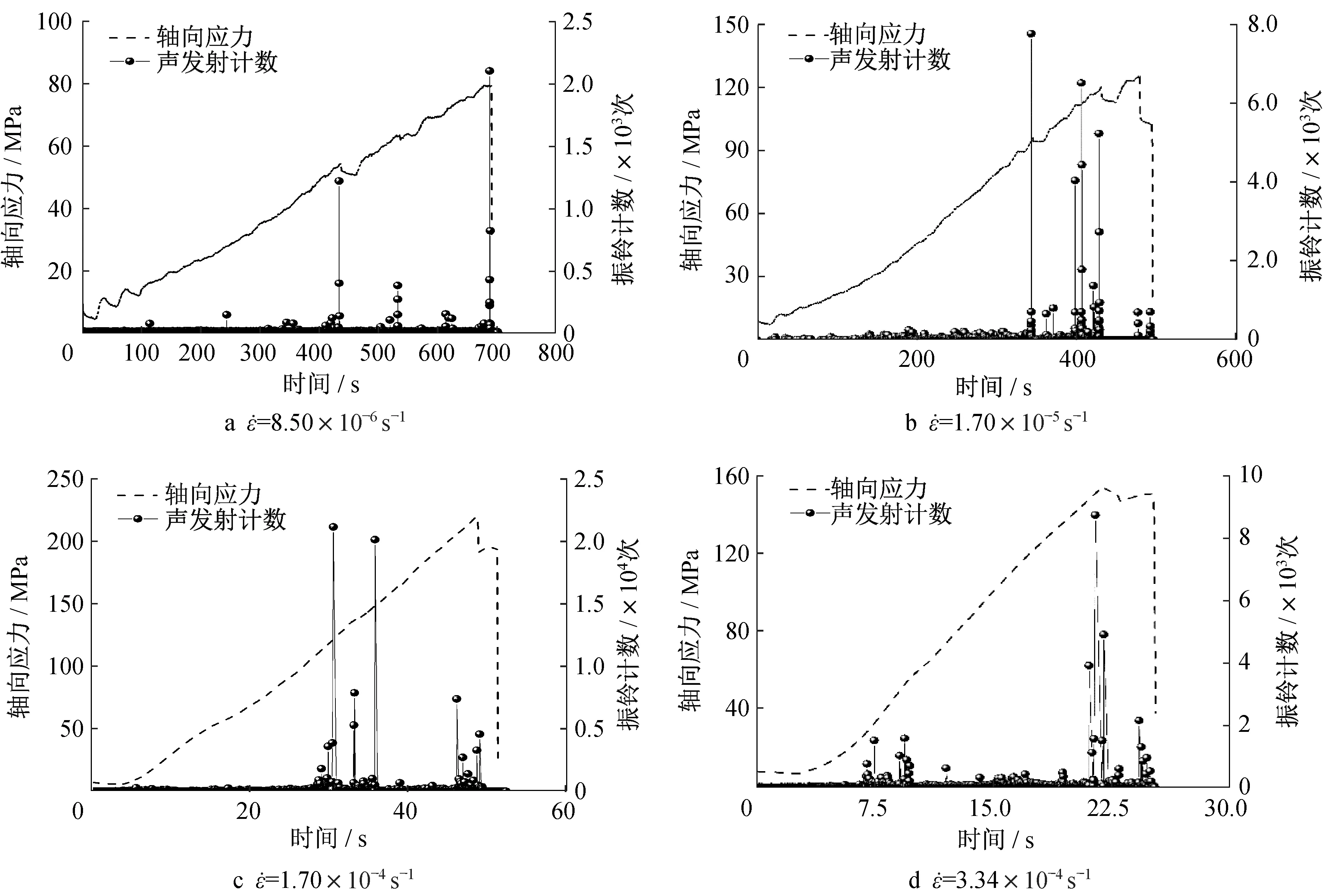
图9 不同应变速率下炭质板岩的振铃计数特征Fig.9 Acoustic emission counting characteristics of carbonaceous slate at different strain rates

2.3.2 主频率特征

声发射信号中的主频率分布可以用来表征岩石的破坏形式［11］。声发射信号中大量的低频组分表明岩石破裂过程中产生了大规模裂纹，而大量的高频组分则表征小规模裂纹的产生［22-23］。图10汇总分析了炭质板岩在不同应变速率下的主频率分布规律。在单轴压缩作用下，不同应变速率下的主频率分布具有明显的分区特征，均可化分为3 个条带：Ⅰ：0～50 kHz、Ⅱ：50～100 kHz、Ⅲ：100～250 kHz。为了更准确地分析应变速率对主频率分布特征的影响，图11统计了不同应变速率下主频率在各个条带内的占比。随应变速率的增加，早期裂纹的萌生和扩展时间较短，低频（Ⅰ：0～50 kHz）范围内的主频率占比呈现逐渐增加的趋势，而高频（Ⅲ：100～250 kHz）范围的主频率占比呈现减小趋势，试样破坏得更严重。

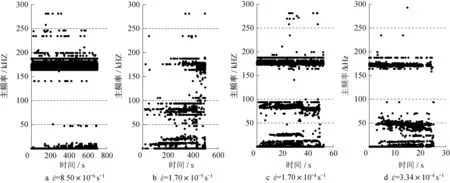
图10 不同应变速率下炭质板岩的主频率分布特征Fig.10 Main frequency distribution characteristics of carbonaceous slate at different strain rates

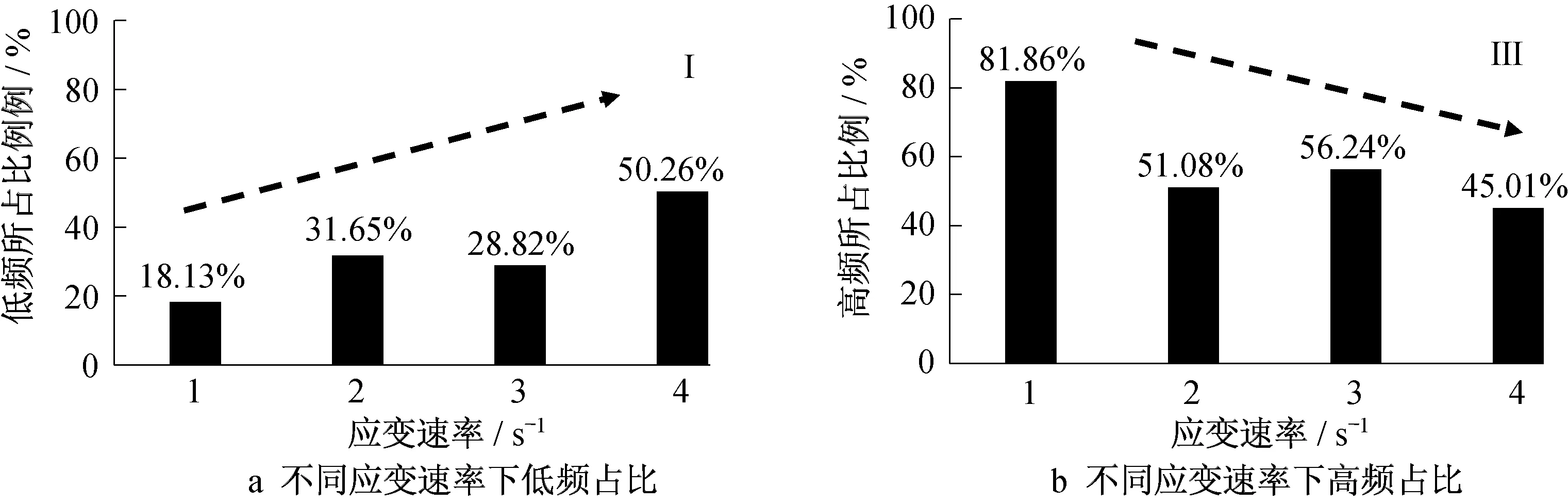
图11 不同应变速率下炭质板岩低频带和高频带的变化特征Fig.11 Variation characteristics of low frequency band and high frequency band of carbonaceous slate at different strain rates

2.4 应变速率对试样破坏特征的影响

炭质板岩在不同应变速率下的破坏形式如图12所示。在单轴压缩作用下，应变速率对炭质板岩的破坏形式影响较大。应变速率为8.5×10-6s-1时，炭质板岩先形成与压力方向平行的裂缝，并有充足的时间扩展、贯通，储存的弹性应变能较小，加载过程中试样损伤较严重，试样呈张拉破坏，破裂面较粗糙。当应变速率为1.7×10-5s-1时，加载过程中储存弹性应变能相对较大，用于破坏时的能量相对较多，脆性张拉裂纹逐渐贯通。随着应变速率进一步增大至1.7×10-4s-1时，原生裂纹不能充分闭合，耗散能占比较小，加载输入能量大部分以弹性应变能形式储存于炭质板岩试样内部；进入裂纹扩展阶段后，过高的弹性应变能使得张拉裂纹和剪切裂纹同时发生，导致耗散能急剧增大，最终形成宏观裂纹，试样呈张拉-剪切复合破坏。当应变速率为3.34×10-4s-1时，高应变速率下储存的大量弹性能使得试样产生剪切滑移面，且剪切滑移面角度较大；在加载后期，剪切面滑移摩擦，大部分弹性能转化为耗散能，破坏程度更加剧烈，试样主要呈剪切破坏甚至崩解破坏。试样的破坏形态与2.3.2 节的主频率分布特征相一致。

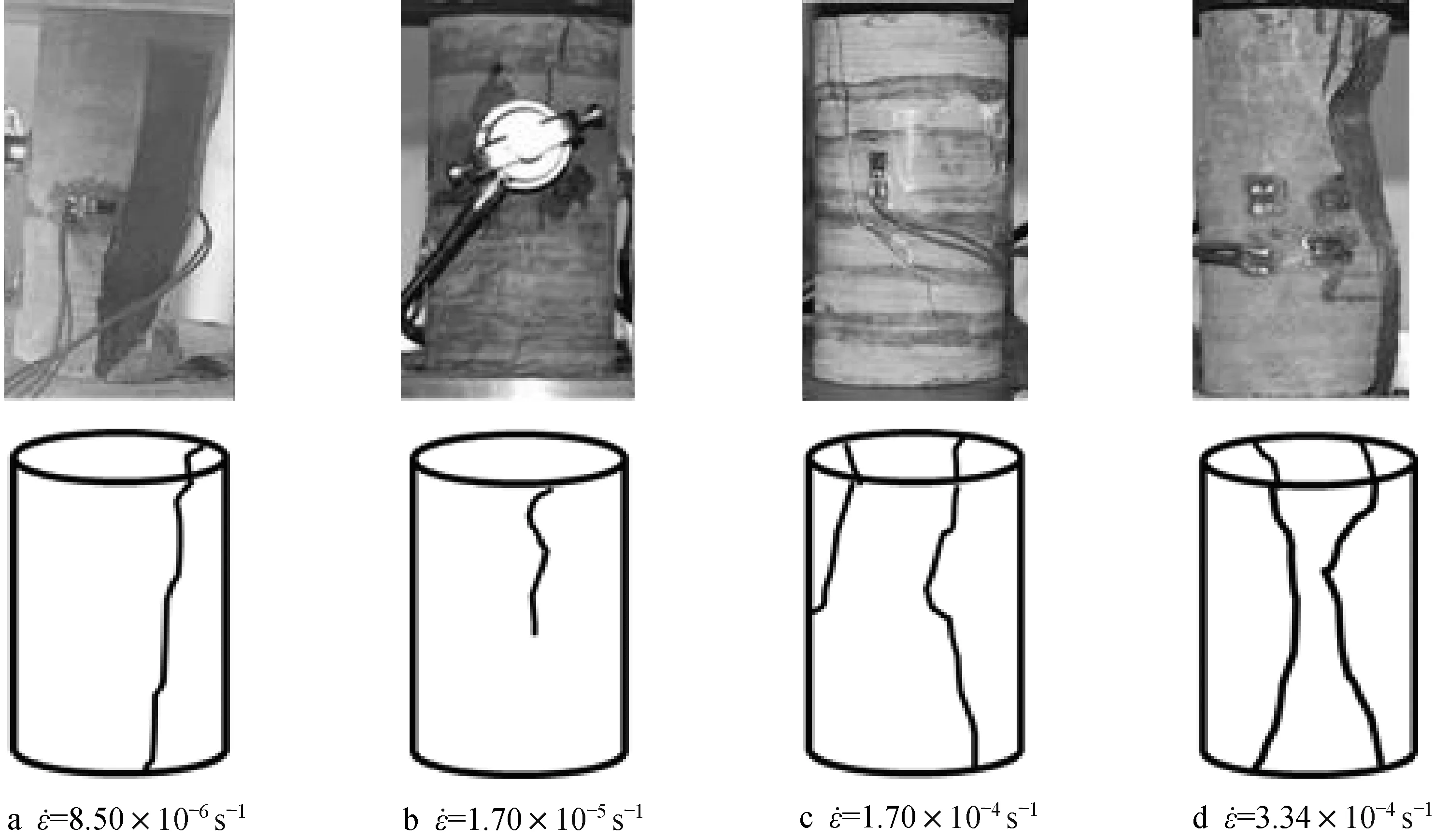
图12 不同应变速率下炭质板岩的破坏形式Fig.12 Failure modes of carbonaceous slate at different strain rates

3 炭质板岩特征应力的确定方法及变化规律

特征应力（闭合应力σcc、起裂应力σci、扩容应力σcd）是表征岩石裂纹形成、发展、贯通的重要指标，是描述岩石渐进性破坏过程的核心指标［24-29］。分析应变速率对特征应力的影响规律，有利于进一步揭示炭质板岩的应变速率效应。

3.1 基于耗散能演化的特征应力确定方法

3.1.1 线弹性阶段耗散能演化理论

假设裂纹闭合点的应力、应变分别为σcc和εcc，单位体积内输入的总能量为Ucc。在线弹性阶段，满足式（5）：

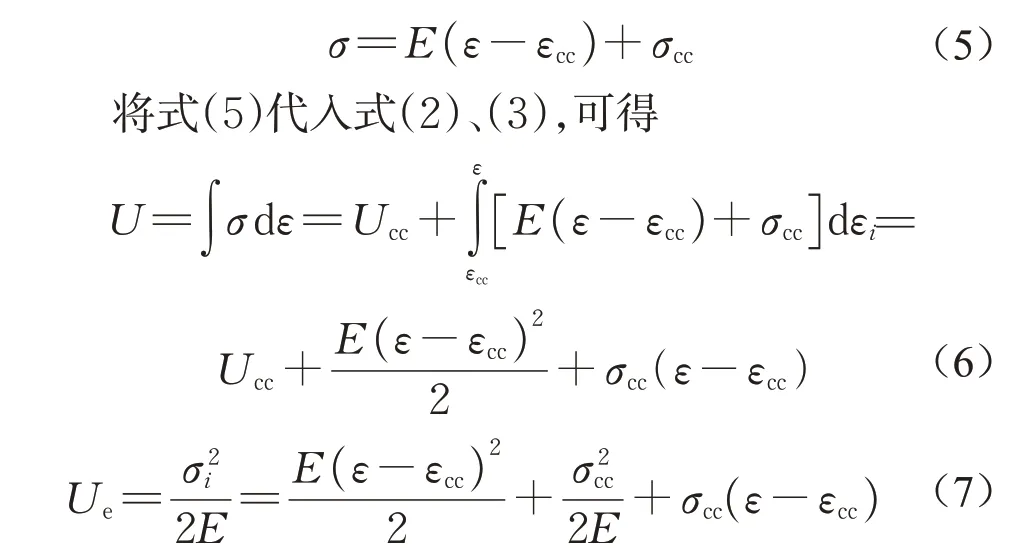
由式（6）和（7）可知，在线弹性段单位体积内弹性应变能和总应变能随应变均呈二次抛物线分布。将式（7）和式（6）代入式（4）可得

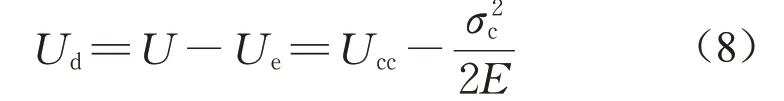
由式（8）可知：在线弹性段，单位体积内耗散能不随应变的增加而改变，保持恒定。因此，可定义耗散能密度曲线斜率为零的起点处应力为裂纹闭合点σcc，耗散能密度曲线斜率零的终点处应力为扩容应力点σcd。

3.1.2 炭质板岩特征应力的确定

图13汇总分析了加载速率为1.7×10-5s-1时炭质板岩的轴向应力及能量变化规律。通过单位体积内耗散能演化特征可将炭质板岩的峰前应力-应变曲线分为3个阶段。

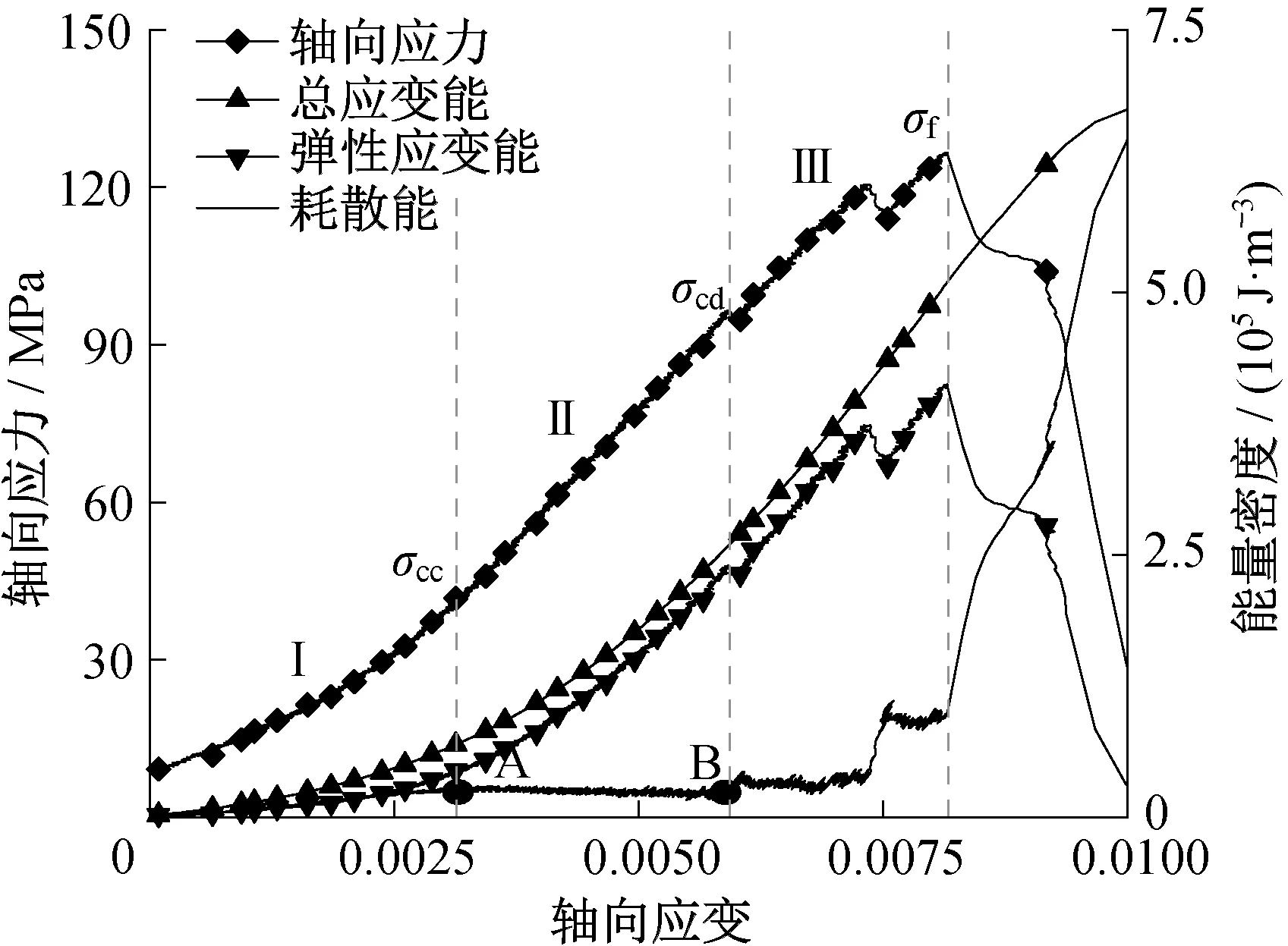
图13 1.7×10-5s-1速率下炭质板岩的应变能发展规律Fig.13 Evolution of strain energy of carbonaceous slate at a strain rate of 1.7×10-5s-1

裂隙闭合阶段Ⅰ：此阶段试样内原生微裂纹逐渐闭合；总应变能的输入一部分转化为弹性能，一部分用于原生裂纹的闭合，从而导致耗散能的增加。该阶段结束的特征应力为裂纹闭合应力σcc［26］。

线弹性阶段Ⅱ：此阶段原生裂纹稳定扩展，总应变能密度及弹性应变能密度均呈抛物线型增长，耗散能密度曲线与横坐标平行，压力机对试样做功均转化为弹性应变能。该阶段结束的特征应力为扩容应力σcd［29］。

裂纹扩展阶段Ⅲ：此阶段裂纹出现不稳定增长，逐渐形成宏观裂纹，耗散能再次增加，且增加速率变快。

在单轴压缩过程中，横向应变对裂纹的扩展较为敏感，尤其在应力-应变的线弹性阶段，仅从轴向应力-应变很难确定起裂应力点的位置。Zhao 等［30］采用声发射方法对起裂应力的确定进行了讨论，认为起裂应力点为累计声发射撞击数离开线性段的位置。图14是应变速率1.7×10-5s-1时累计声发射撞击数随应力的演变规律。随着轴向应力的增加，累计声发射撞击数先缓慢增加；在线弹性阶段内，累计声发射撞击数增长较平稳，基本呈线性；随着裂纹的出现，累计撞击数偏离线性位置，故该点可作为炭质板岩的起裂应力点。

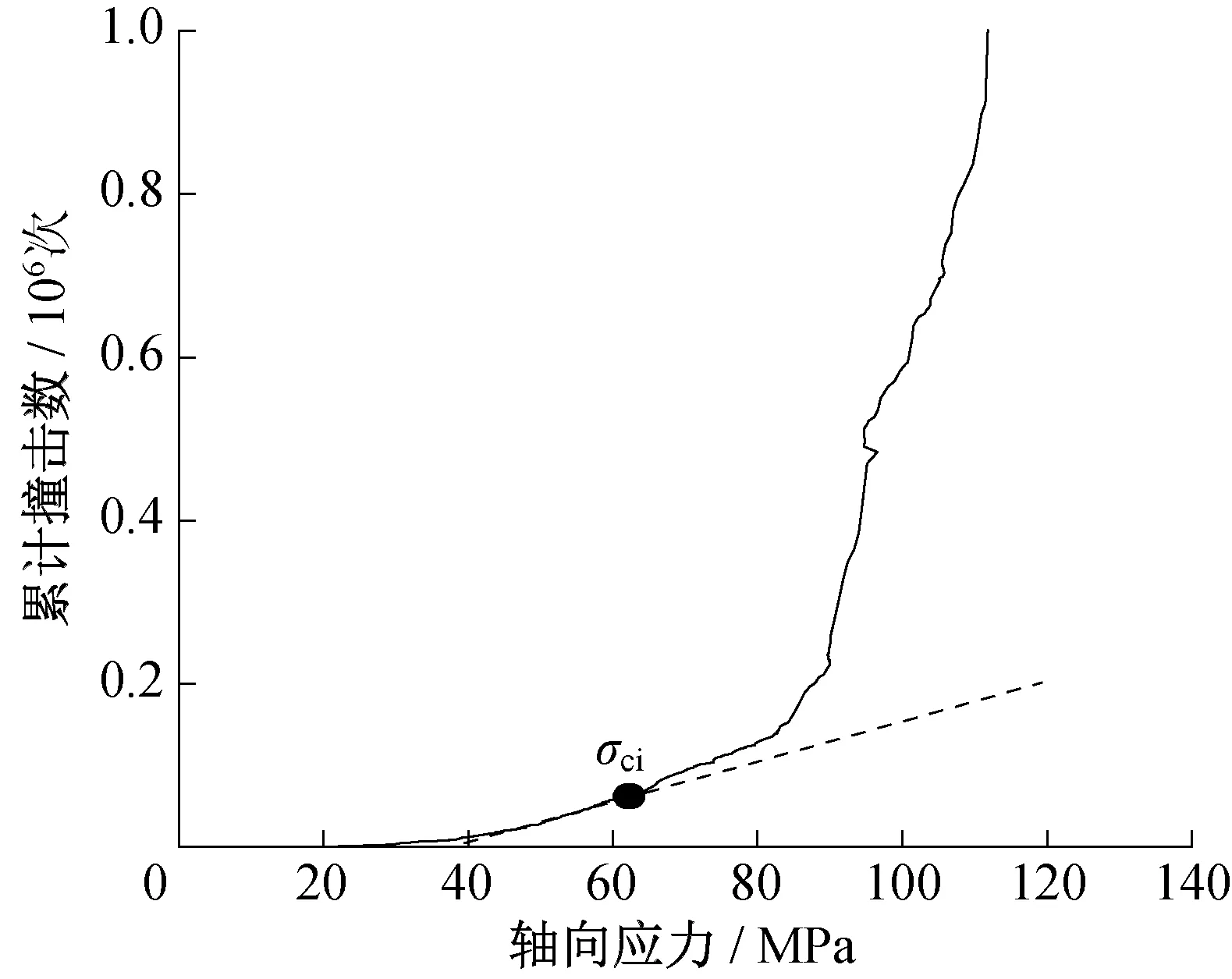
图14 炭质板岩累计声发射撞击数Fig.14 Cumulative acoustic emission impact number of carbonaceous slate

3.2 应变速率对特征应力的影响

采用3.1节方法确定不同应变速率下炭质板岩的特征应力，如表1所示。当应变速率从8.5×10-6s-1增加至1.70×10-5s-1时，σcc、σci和σcd的平均值均逐渐增大，当应变速率为3.34×10-4s-1时，σcc、σci和σcd的平 均值出现了减小，如表2所示。

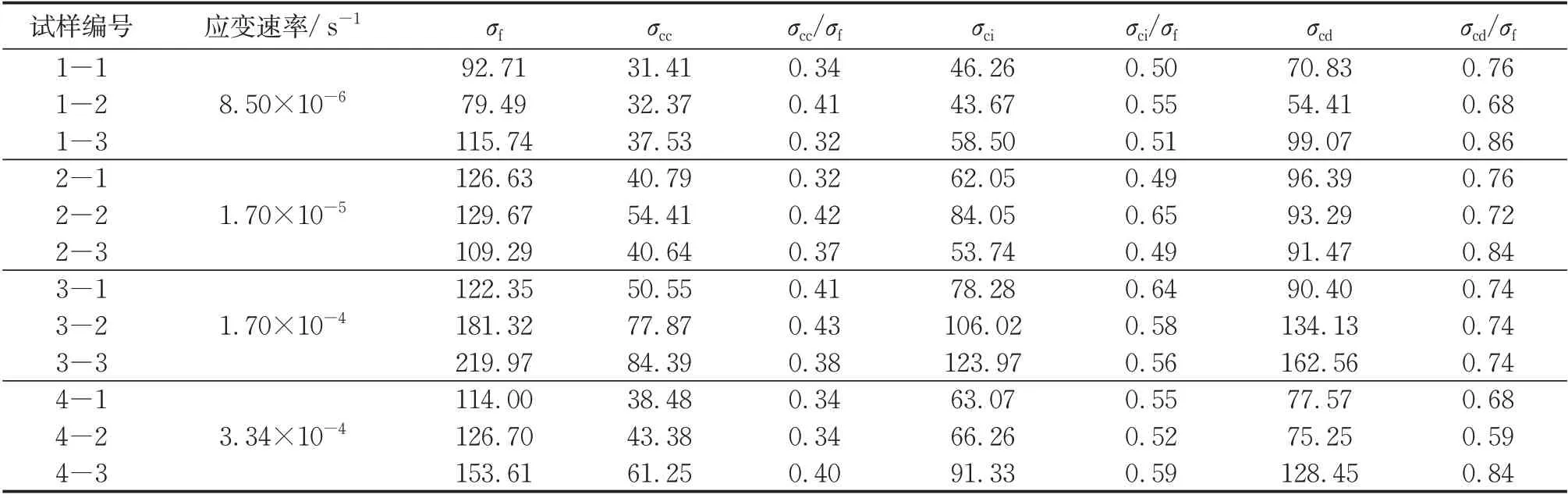
表1 不同应变速率下炭质板岩特征应力Tab.1 Characteristic stress of carbonaceous slate at different strain rates

表2 不同应变速率下炭质板岩特征应力平均值Tab.2 Mean characteristic stress of carbonaceous slate at different strain rates

图15 汇总了不同应变速率下各特征应力与峰值强度的比值。随着应变速率的增加，各特征应力与峰值强度的比值虽有变化，但变化范围较小，可近似为定值，其中σcc/σf约为0.37，σci/σf约为0.55，σcd/σf约为0.74。因此，应变速率虽会对炭质板岩的特征应力及峰值强度造成影响，但对各特征应力与峰值强度的比值几乎无影响。

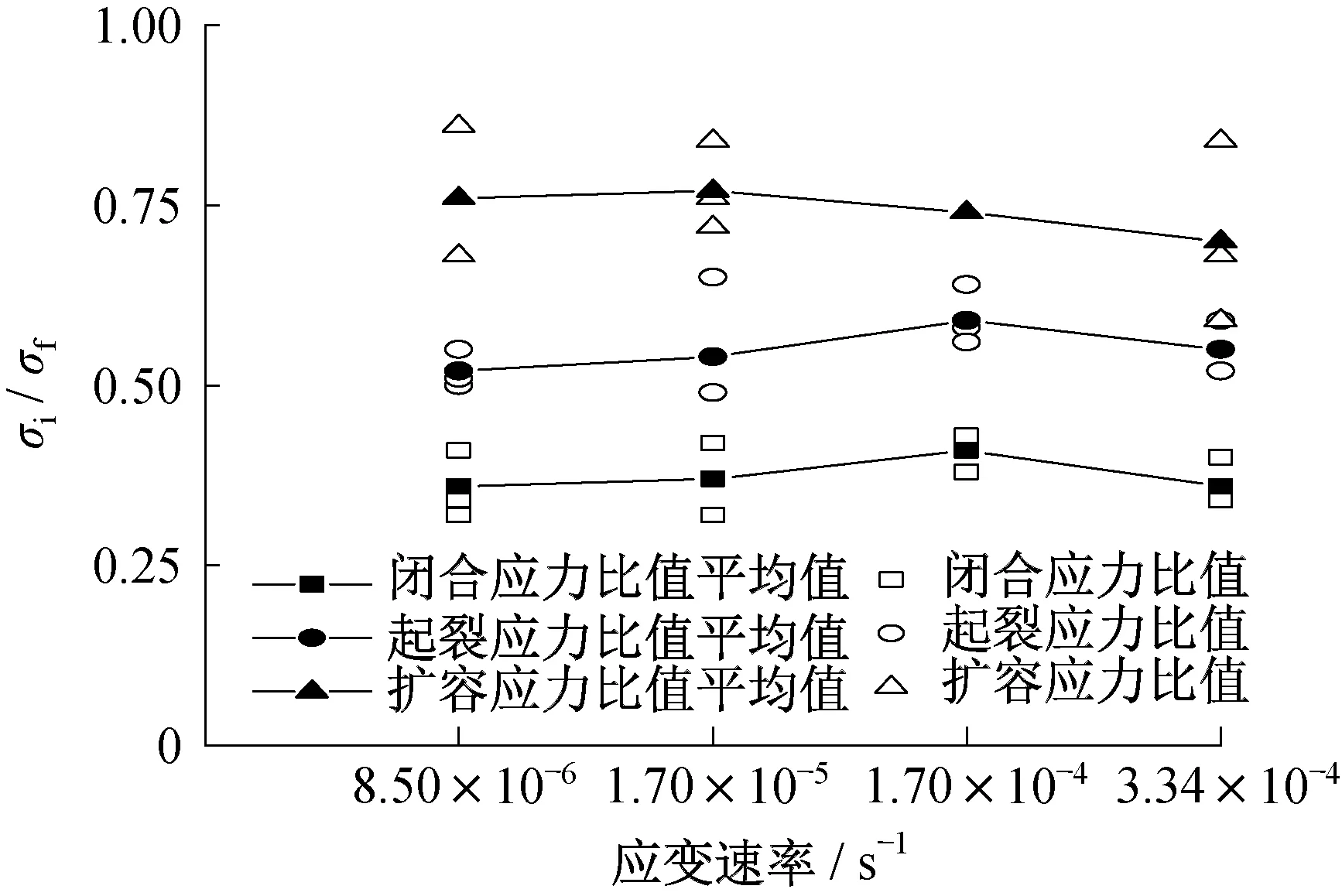
图15 不同应变速率下炭质板岩特征应力变化规律Fig.15 Characteristic stress variation of carbonaceous slate at different strain rates

4 结论

在准静态应变速率范围内开展了4种不同应变速率下的单轴压缩试验，分析了应变速率对炭质板岩力学响应及声发射特征的影响，探究了应变速率对炭质板岩破坏机制的影响，并提出了基于耗散能密度演化的特征应力确定方法，形成了以下结论：

（1）在单轴压缩过程中，炭质板岩在准静态应变速率范围内存在明显的应变速率效应：随应变速率的增大，峰值强度和弹性模量先增大后减小，峰值强度和弹性模量在1.70×10-4s-1时达到最大，平均值分别为174.55 MPa和27.16 GPa。

（2）在单轴压缩过程中，声发射信号中低频信号占比随应变速率增加逐渐增加，高频信号占比逐渐减小，试样破坏程度愈加剧烈，且破坏形式由张拉破坏逐渐转为剪切破坏，在应变速率8.50×10-6s-1时主要为张拉破坏，在应变速率3.34×10-4s-1时主要为剪切破坏。

（3）炭质板岩的闭合应力、起裂应力和扩容应力与峰值应力的比值不随应变速率发生变化，基本为定值，分别约为0.37、0.55和0.74。

作者贡献声明：

肖颖鸣：开展试验，数据处理及分析，图表呈现，论文撰写和返修。

乔亚飞：论文概念设计，论文指导和修改，基金提供。

李红儒：协助开展试验。

何满潮：工程现场协调，基金提供。