基于地下水入渗反演解析的污水管网破损数值化定位
徐祖信,王思玉,刘淑雅,尹海龙,楚文海
(1. 同济大学环境科学与工程学院,上海 200092;2. 同济大学污染控制与资源化研究国家重点实验室,上海 200092;3. 同济大学长江水环境教育部重点实验室,上海 200092;4. 同济大学上海污染控制与生态安全研究院,上海 200092)
截至2020 年,我国城市排水管道总长约80.2 万km[1],其中,近一半排水管道使用年限超过10 年,管网老化增加了管网破损的几率[2]。在污水管道埋设于地下水位之下的地区,污水管道破损导致的地下水入渗问题严重。调查显示,我国南方部分城市污水管道的地下水入渗量可达3 800~6 300 m3·(km·d)-1,部分地区入渗量可占污水量的42%~66%[3-4]。入渗地下水侵占了管道容量,虚高了城市污水处理率,影响污水处理厂处理效能[5-6]。因此,污水管道破损检测十分重要,破损管段定位有助于管道修复和改造。
目前,污水管道破损诊断主要应用检测设备,如管道闭路电视(CCTV)和潜望镜检测(QV)等,通过实时影像反映管道内部结构,直接确定管道破损位置[7-9]。设备检测定位精度高,但是价格昂贵,难以全面推广应用。此外,基于水量、水质监测数据解析水量来源,可间接判断管道状况,如最小流量法和三角分析法等可对封闭片区污水管道的地下水入渗情况进行评估[10-11],操作简便但定位精度低,难以获得准确的破损位置。
本文创新性建立了高地下水位地区污水管道破损的数值化定位技术,将污水管道破损识别转化为入渗地下水量的识别,晴天条件下对管道中的污水和地下水水量进行解析,判断管道是否破损或者破损是否严重。进入管网的污水和地下水属于管网系统流动模拟的外部边界条件,由此,这个问题在管道水动力数学模拟上属于已知管道内部流动求解外部边界条件,是数学上的反演问题[12-14],通过启发式算法进行寻优搜索[15],确定入渗地下水量和入渗点位,从而识别污水管网破损点位和管段。本研究方法无需开挖地面,不干扰污水管道的运行,有限节点的水位监测成本低,容易实施。
1 研究方法
1.1 基于检查井水位的流量计算方法
基本原理是通过管道实际流动的监测来计算分析区域的边界条件。由于污水管道的流量监测存在操作复杂、成本高等问题,通过管道检查井的水位监测来计算管道流量。根据管渠水力学计算原理[16],流量计算公式为
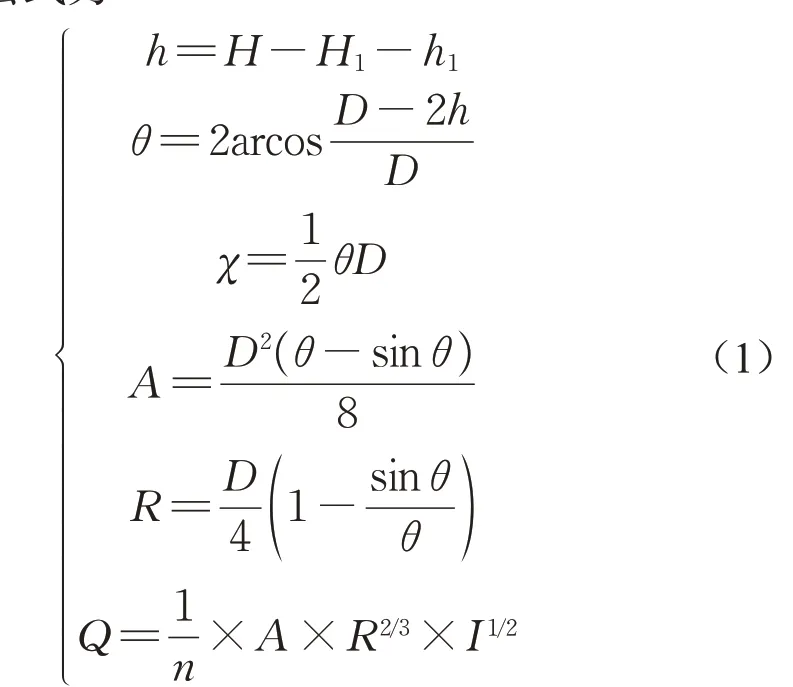
式中:h为下游管道水深,m;H为检查井地面高程,m;H1为管底标高,m;h1为地面至水面高度,m;θ为水流中心夹角,rad;D为管径,m;χ为湿周,m;A为过水断面面积,m2;R为水力半径,m;Q为管道流量,m3·s-1;n为管道粗糙系数;I为水力坡度。
1.2 基于寻优定位模型的破损节点诊断
污水管网系统的水流运动由管网拓扑结构和边界条件共同确定。当管网拓扑结构一定时,任意管段或节点发生地下水入渗,都会引起管网内水流运动改变。根据此特性,可以反向解析地下水的入渗量和入渗位置。我国城市污水管网破损点较多,地下水入渗量的直接逆向求解比较复杂。因此,采用寻优分析方法将反问题转化为正问题参数寻优问题,寻找适配的边界条件,使得污水管网水动力模拟数据和检查井监测数据误差小于允许误差,技术路线如图1 所示。由此可见,污水管道破损寻优定位模型的实质就是遍历所有管网节点地下水适配方案,寻求实际入渗量的过程。
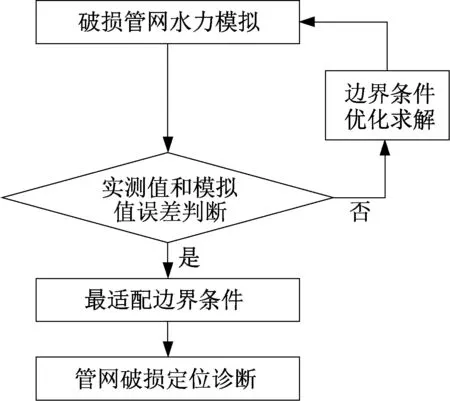
图1 污水管网破损诊断技术路线Fig.1 Technical roadmap of sewer defect diagnosis
污水管道破损寻优定位模型包括两部分,一是污水管网水动力模型,二是寻优定位模型。
1.2.1 污水管网水动力模型
污水管网水流运动可用圣维南方程组描述,如式(2):
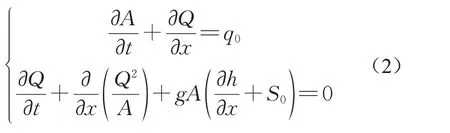
式中:t为时间,s;x为沿水流方向管道的长度,m;q0为单位管长上的旁侧入流,m3·s-1;g为重力加速度,m·s-2;S0为管底坡度。
采用InfoWorks ICM 模型模拟污水管网中的流动状况。在InfoWorks ICM 中,管道的旁侧入流可通过节点外部入流输入。在晴天工况下,城市污水管网外部入流主要包括接纳的污水和入渗地下水,因此,在管网模型节点上,有

1.2.2 寻优定位模型
寻优定位模型主要由决策变量、目标函数和约束条件共同组成。
(1)决策变量。决策变量为待求的各节点地下水入渗水量,由于全部节点都有可能发生地下水入渗,破损节点的优化维度直接由管网的节点数确定。
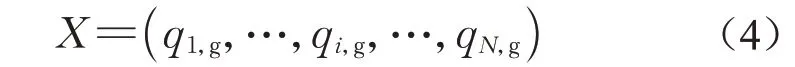
式中:qi,g为节点i的地下水入渗量,m3·s-1;N为污水管网的总节点数。
(2)目标函数。目标函数表达为监测点的实测水位与模拟水位的最小均方根误差,如式(5)所示:

式中:X*为地下水入渗适配方案;Ns为监测点数量;T为管网模拟时间序列;h1,s和h2,s分别为监测点s处的模拟水位和监测水位;Ks为模拟的时刻数目。
(3)约束条件。在污水管道破损寻优定位过程中,除了保证总的节点地下水入渗量与污水管网系统的地下水入渗总量一致,还需满足污水管网的水力平衡条件,包括节点连续性方程和管段能量方程,如式(6):
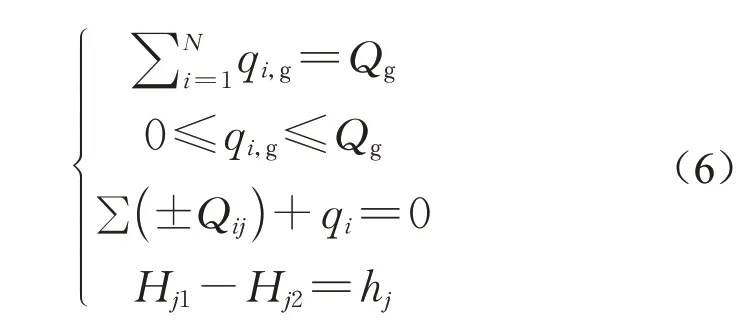
式中:Qg为污水管网系统整体的地下水入渗量,m3·s-1;Qij为与节点i连接的各管道流量,m3·s-1;qi为节点i的流量,m3·s-1;Hj1为管段j上游节点水头,m;Hj2为管段j下游节点水头,m;hj为管段j的压降,m。
1.2.3 基于粒子群优化算法的模型求解
污水管道破损寻优定位模型的求解空间随着管网结构复杂程度的增加呈指数型增长,可借助启发式优化算法完成入渗地下水分配方案的试算过程。
粒子群优化算法(Particle Swarm Optimization,PSO)[17]是一种基于群体智能理论的优化算法,由于其特有的记忆性和简单的算法结构,已被广泛应用于多个研究领域,如供水管网爆管定位[18]、排水管网设计[19]、排水管网污染源溯源[20]等。在各种改进粒子群算法中,基于随机权重策略的PSO算法能在一定程度上避免多峰函数陷入局部最优[21-22]。选择基于随机权重策略的PSO算法进行模型求解,完成地下水分配方案的持续自反馈寻优过程。具体步骤如下:
(1)初始粒子群生成:随机产生多个粒子,初始化粒子群。每个粒子的位置向量代表一种地下水分配方案,其中每个维度代表一个节点的地下水入渗量;粒子的速度向量控制着粒子飞向最优解。
(2)目标函数值评价:将粒子代表的地下水分配方案嵌入到水动力模型中,基于模拟结果计算粒子的目标函数值,以衡量个体的优劣性,根据目标函数值确定粒子和粒子群的最优位置。
(3)粒子群进化:更新每个粒子的位置向量和速度向量,产生新一代的粒子群。并与上一代粒子群进行比较,更新每个个体的历史最优位置和粒子群的全局最优位置。在更新粒子速度时引入了随机惯性权重策略。惯性权重是平衡算法全局与局部搜索能力的最重要参数,利用随机变量改变惯性权重可以帮助算法跳出局部最优,在迭代后期不易发生目标函数值停滞现象,保证粒子群的多样性[21]。
(4)迭代终止:当目标函数值小于给定误差范围或满足迭代次数时结束计算,得到全部节点的地下水最适配方案,否则重复上一步,直到满足终止条件。
基于ICM Exchange 模块实现污水管道破损寻优定位模型的构建和求解,ICM Exchange 能够在Ruby开发环境下对默认封装的InfoWorks ICM模型进行外部调用,从而实现与MATLAB 软件运行文件的交互。因此,利用ICM Exchange 平台,在MATLAB开发环境下,实现InfoWorks ICM管网模型和PSO算法的耦合(图2)。该耦合模型能够实现管网节点地下水适配方案的自动设计,并在水力平衡和目标函数的约束下对参数空间进行充分搜索,直至得到最小误差解。
1.3 污水管道节点破损程度评价方法
寻优定位模型最终解析的是各节点的地下水入渗量,为了更好地评价各节点是否为破损点,通过管段破损状况进行评估。《室外排水设计标准》(GB 50014—2021)[23]给出了单位管长、单位管径地下 水 入 渗 量ε的 限 值 为0.01~1.0 m3·(d·mm·km)-1。参照这一标准值,建立如表1的评价方法。
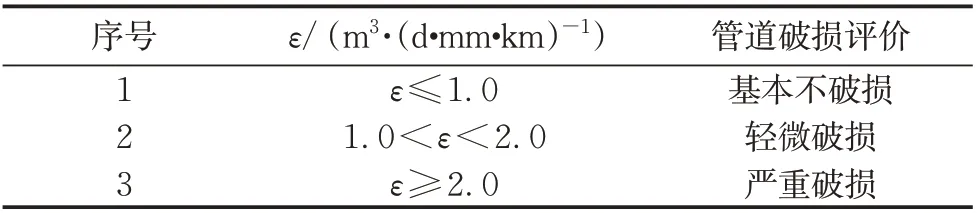
表1 污水管道破损评价方法Tab.1 Evaluation method for damage to sewage pipes
2 案例应用
2.1 研究区域概况
研究区域为安徽省某市HS 污水泵站服务范围涉及的污水管网系统(图3 a),区域总面积约3.93 km2,污水管道总长约9 km,污水管网封闭、独立,主要接纳区域内居民生活排放的污水。
首先建立研究区域的污水管网和污染源综合地理信息系统(GIS 系统,见图3 b),确定该污水系统接纳的生活污水总量约5 305 m3·d-1。根据污水泵站旱天进水水量记录,确定该污水泵站晴天进水量约11 156 m3·d-1。因此,基于水量平衡可确定该系统地下水入渗总量约5 184 m3·d-1,占晴天总水量的49%,说明研究区域内污水管网系统整体破损情况严重。
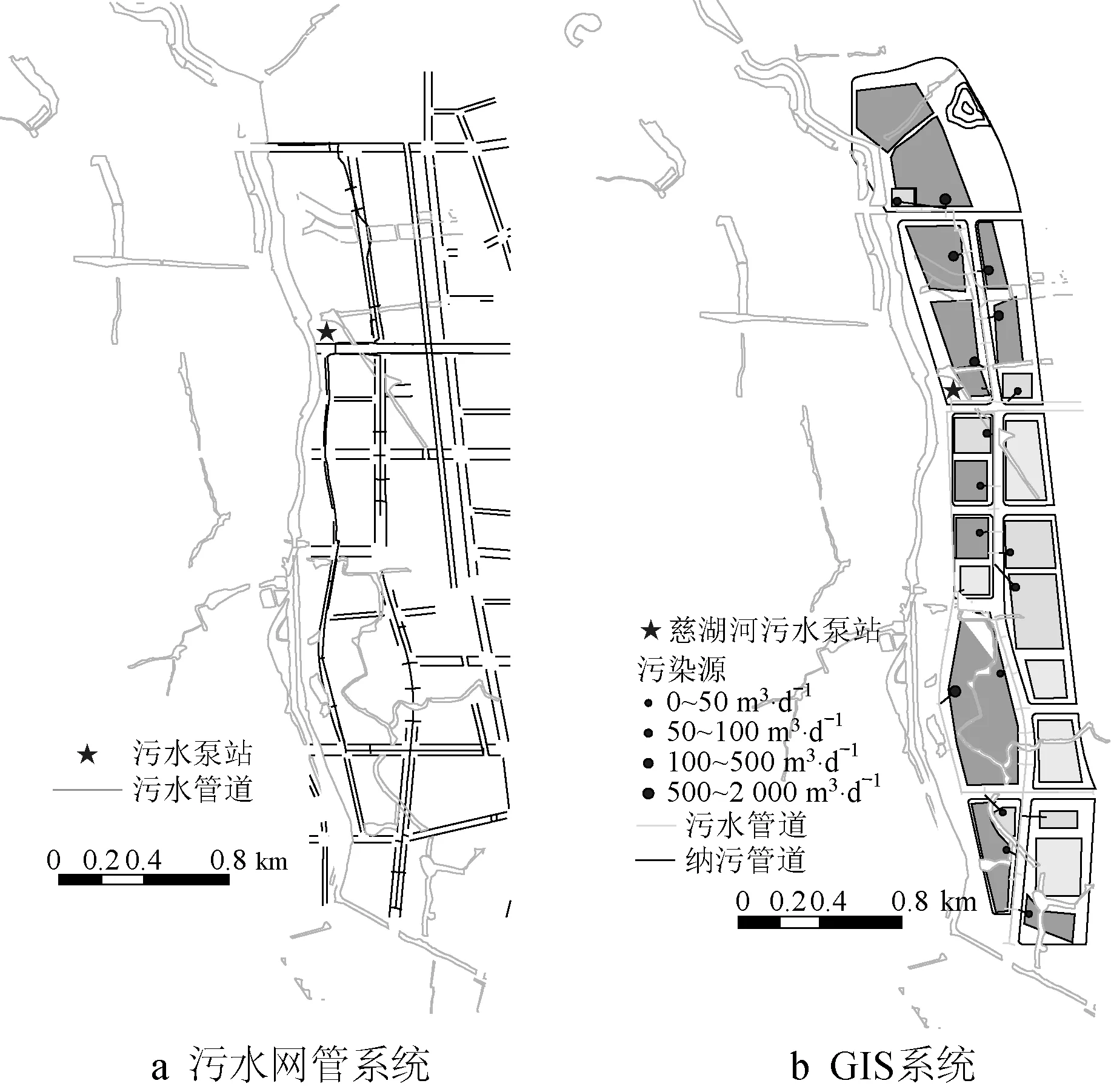
图3 研究区域示意Fig.3 Schematic diagram of the area studied
2.2 检查井水位监测及流量计算
研究区域内的污水管网共有100 个检查井,全部进行水位监测,监测时间为2021年10月28日,前期晴天数为7 天,每个检查井分别于高水位时段(10:00—11:00)和低水位时段(15:00—16:00)各监测1 次,监测时刻是根据泵站实测水位的变化情况确定的,以获取各检查井的高、低水位,计算平均值。现场工作分为7 个小组同步开展,以保证在同一时间段内完成全部监测工作。
城市污水管网晴天输送水量一般仅包括生活污水和地下水。日均生活污水的波动性不大,地下水入渗量主要和破损程度相关,一般认为地下水日入渗水量是恒定的[24]。因此,假设晴天时污水管网流动是恒定流,取fs(t)=fg(t)=1,通过检查井日平均水位可以计算日平均流量(图4)。
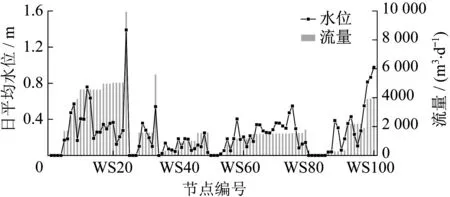
图4 节点日平均水位及流量Fig.4 Water level and flow of manholes
2.3 破损点位的确定性分析
为了减小计算工作量,提高计算精度,排水管网水动力模拟前通常需要根据流动性一致原则进行管网概化。概化后的管网共有99条管道,节点数与检查井数一致。根据连续性方程,管道节点下游出水量和上游进水量的差值为该节点的外部入流量(包括接纳的生活污水和入渗地下水),因此节点地下水入渗量为
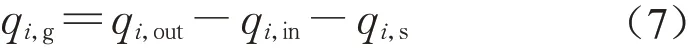
式中:qi,out为节点i下游出水量,m3·s-1,通过该节点水位计算得到;qi,in为节点i上游进水量,m3·s-1,通过上游节点水位计算得到;qi,s为节点i的生活污水接纳量,m3·s-1,根据建立的研究区域污水管网和污染源GIS系统确定。
对全部节点建立连续性方程,结合图4 所示节点流量水位关系,可以确定性求解出全部节点的地下水入渗量,节点破损计算分析结果如表2 所示。从中可以看出:研究区域内共存在16 个破损节点,其中2 个节点为轻微破损,14 个节点为严重破损。破损节点的总地下水入渗量为5 050 m3·d-1,与污水管网总水量平衡解析结果相比,其相对误差小于5%,说明计算结果可靠。

表2 实际破损节点及其地下水入渗量Tab.2 Actual damaged nodes and their groundwater infiltration
2.4 有限监测节点下破损点位定位寻优解析
污水管网的监测点数量会影响计算结果的准确程度,水位监测节点若少于实际检查井数量,会直接影响寻优定位模型诊断的精度。但是,在实际工程中,对所有检查井监测水位较为困难,有必要继续探讨检查井监测数量和模型计算精度之间的关系。为探究最佳监测点数量,采用均匀布点,选取占总节点数20%、30%、40%、50%、60%、70%、80%共7种工况进行分析。
运用InfoWorks ICM水力模型耦合PSO算法自动反演计算时,设置粒子维度为100,粒子群规模为80,进化代数为300,学习因子均为2。为了避免粒子出现早熟收敛现象,引入随机惯性权重来提高算法的收敛速度和全局收敛性。图5展示了60个监测点数量工况下目标函数的变化情况,大致可分为3个阶段:在迭代初期目标函数值离散分布,经过20代后,目标函数值从0.042 快速减小到0.035;在迭代中期,目标函数值逐渐密集,减小速度变缓;在迭代后期,目标函数值逐渐收敛,最终趋近于最优值0.026。由于PSO 中的粒子具有记忆性,可将历史最优位置传递给其他粒子,因此目标函数是朝着同一方向逐步下降的[21]。
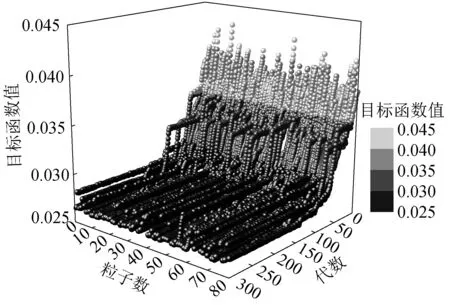
图5 基于粒子群算法的管网模型寻优过程Fig.5 Process of sewer modeling optimization based on PSO algorithm
不同监测点数量工况对应的寻优定位结果见图6、图7和表3。当监测点数量较少时,模型定位存在较大偏差。20 个监测点寻优定位结果是32 个模拟破损节点,实际上,其中只有11个为实际破损点,误差较大,主要原因是监测点数量过少,模型的约束条件和目标函数无法限制反演参数的多种组合方式,难以寻出最优解。随着监测点数量的增加,约束条件和目标函数也随之进行了调整,模型的定位结果也逐渐改善。当增加到80个监测点时,模型正确定位到了全部实际破损点,如图6 g 所示,表明不需监测全部检查井水位在计算上是可行的。
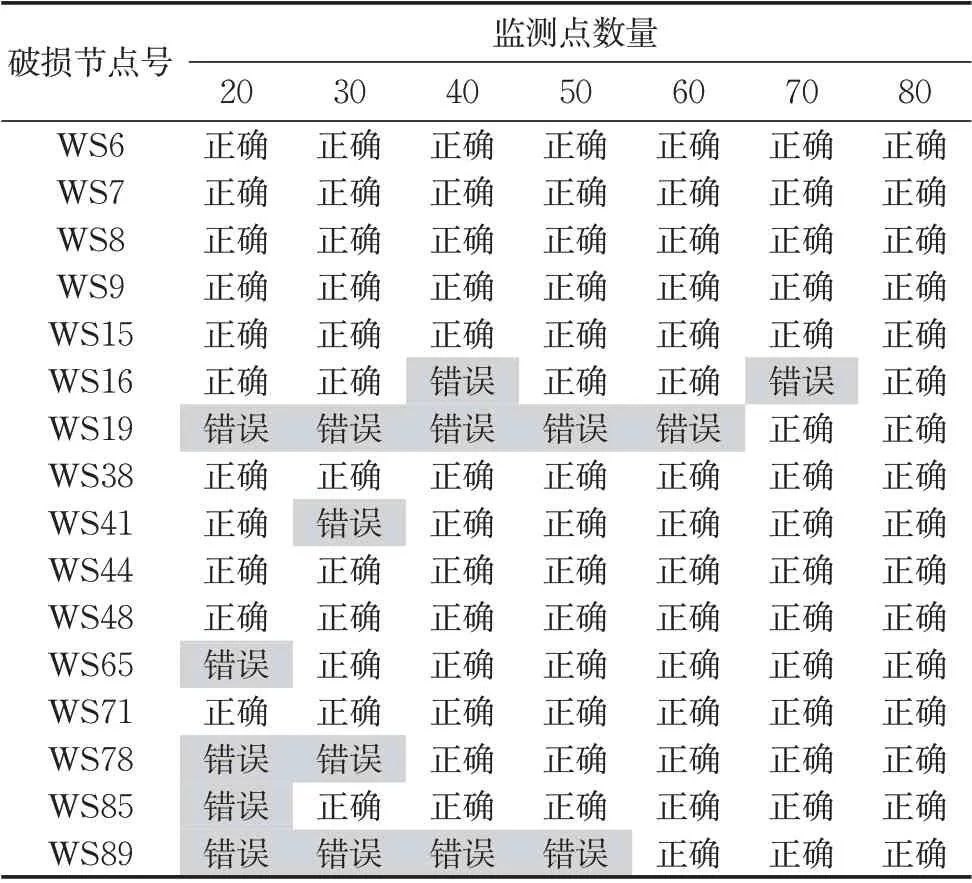
表3 不同监测点工况下实际破损节点处定位结果Tab.3 Positioning results at actual damaged points under different monitoring point conditions
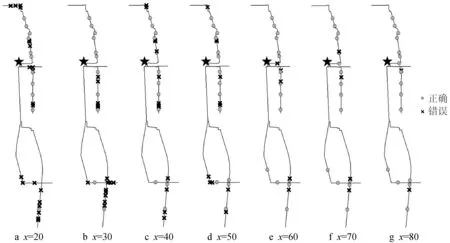
图6 不同监测点工况下模型的定位结果Fig.6 Location results under different monitoring point conditions
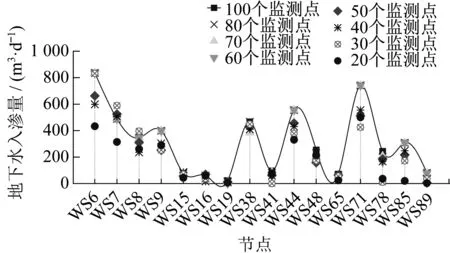
图7 不同监测点工况下实际破损点的地下水入渗量反演计算结果Fig.7 Inversion calculation results of groundwater infiltration at actual damaged points under different monitoring point conditions
为了进一步说明监测节点数对寻优定位结果的影响,建立定位查准率和定位查全率指标对模型的定位效果进行评价。定位查准率直接从模型的诊断结果出发,衡量模型定位结果的有效性;定位查全率从实际情况出发,衡量模型是否能尽可能多地定位到真实的破损节点。对应表达式如式(8)、式(9):式中:P为定位查准率;NT为模型模拟破损正确的全部节点数;ND为模型模拟破损的全部节点数;R为定位查全率;NP为实际破损的全部节点数。
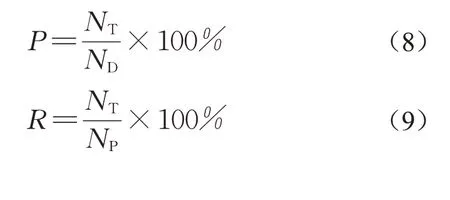
定位查准率和定位查全率与监测点数量呈正相关关系,在60 个监测点处,定位查准率的斜率发生陡增,定位查全率与70 个监测点处相当(图8)。因此,在同时考虑模型定位精度和监测成本的情况下,推荐60个监测点为最佳工况,此时模型正确定位到了15个实际破损点,误判了5个节点,均位于实际破损点周边1个节点处,定位查准率为75%,定位查全率为94%。若对定位到的实际破损点及其上游管道进行修复,可相应减少5 028 m3·d-1地下水入渗量,由此可见,基于有限监测节点的破损寻优定位技术可行、有效。相比于全范围内的CCTV检测,可以大幅度减少现场排查的工作量,降低人力、物力成本。
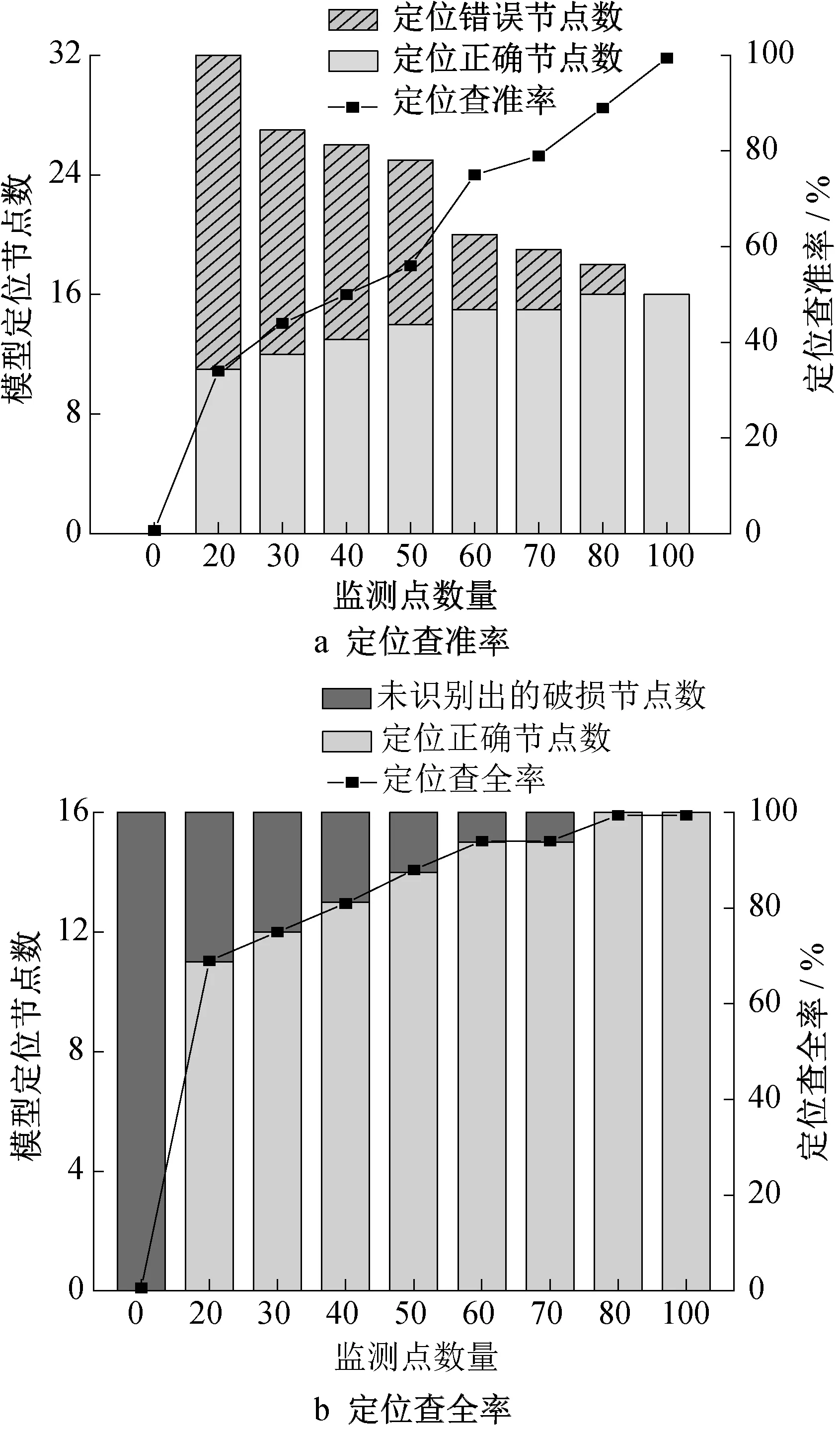
图8 不同监测点工况下定位查准率与定位查全率Fig.8 Location precision rate and location recall rate under different monitoring point conditions
3 结语
创新了高地下水位地区基于有限检查井水位监测的管道破损数值化定位技术,采用InfoWorks ICM模型与PSO算法耦合的方式,建立了具有自我反馈调节机制的破损寻优定位模型。通过构建污水管道外部入流与检查井水位的响应关系完成节点地下水入渗方案的自动设计和动态寻优,可以有效进行污水管道破损点诊断,实现了低成本、无干扰的污水管网破损点数值化定位。
实证研究表明,寻优定位结果的精度与监测点数量相关。通过不同监测点数量的寻优定位结果分析,根据定位精度与技术经济可行性综合比较,推荐监测点是总节点数的50%~60%较为合理,此时定位查准率为75%,定位查全率为94%。对这些节点及其上游管段进行修复,可减少污水管网系统97%的地下水入渗量,显著提升污水管网的运行效能。
综上,本文创新的污水管网破损数值化解析定位方法有效可行、应用简便、经济实用,在我国城市污水治理提质增效中有重要作用。
作者贡献声明:
徐祖信:研究整体指导、论文修改。
王思玉:数学模型构建、论文撰写。
刘淑雅:数据采集。
尹海龙:研究方法指导。
楚文海:论文审阅与修订。

