基于近场动力学均匀化的混凝土防渗墙等效损伤模型

孙 伟，包世诚，张 嘎

（1. 中山大学土木工程学院，广东 广州 510275；2. 清华大学水沙科学与水利水电工程国家重点实验室，北京 100084）

由于能良好地适应基础条件、就地取材、充分利用建筑物开挖渣料、造价较低等优势，土石坝是坝工建设中最有发展前景的坝型之一。防渗结构是高土石坝安全的生命线［1］，处于覆盖层内的混凝土防渗墙受力条件复杂，在巨大水推力、土压力及不均匀沉降作用下，可能会出现局部破损，对坝基渗透稳定性及坝体安全产生不利的影响。同时，高土石坝-混凝土防渗墙是一个多尺度相互作用的系统，存在着千米级的山体、百米级的大坝、米级的防渗体、厘米级的结构面乃至毫米级的裂缝及更小尺度的土体颗粒等多个尺度，这些不同尺度之间的相互耦联和相互作用共同决定了该复杂系统的性能演化和全寿命周期过程（图1）。因此需要发展多尺度数值分析方法，以更精确地刻画上述多个尺度之间的相互作用和更合理地揭示墙体复杂的破损机制。

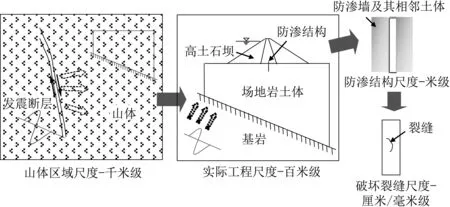
图1 高土石坝-防渗结构多尺度相互作用系统Fig.1 Multi-scale system of the high embankment dam and its prevention structures

学者们基于现场监测、模型试验和数理分析等各种手段，对高土石坝防渗墙应力变形规律和破损机理等开展了研究，取得了很多进展。在现场监测方面，Rice 和Duncan［2］详细分析了美国境内多座坝体防渗结构的服役情况。在模型试验方面，主要以采用土工离心模型试验的方法为主［3］。在数理分析方法方面，目前多采用有限元方法，在高土石防渗墙结构的应力变形［4］、接触模拟［5］、接头型式［6］和水力耦合［7］等多个方面取得了进展。本文主要研究防渗墙结构的破损开裂分析方法。何四清［8］测定了塑性混凝土的断裂特性，并用弥散裂缝模型对册田水库副坝混凝土防渗墙进行了断裂破坏分析；Rice 和Duncan［9］通过安全度计算分析，指出防渗体最大可能开裂的位置为覆盖层与基岩接触的部位；Yu等［10］采用塑性损伤模型模拟了墙体的损伤破坏；冯蕊等［11］基于弥散裂缝模型分析了长河坝坝基廊道的开裂；Cen 等［12］使用细观随机损伤模型分析了面板挤压破损问题等。然而高土石坝中的混凝土防渗墙，因其受力条件复杂，所以破损的多尺度精细化分析方法及据此得到的破损机理规律等研究工作仍需加强。孙伟［13］基于Peridynamics［14-16］（PD，即近场动力学）理论，提出了高土石坝防渗墙破损的PD-FEM（Finite element method）并发式多尺度精细化分析方法。该方法可以实现百米级大坝尺度中毫米级裂缝的精细模拟与扩展演化，较为真实地再现了混凝土防渗墙中拉剪耦合裂缝起裂与扩展形态［17］。相比弥散裂缝模型或损伤模型等，能够得到更具体准确的分离式的裂缝位置和形态；相比DEM（Discrete element method）-FEM 等方法［18］，则可避免DEM 细观参数可能难以确定以及用于实际工程时颗粒大小需要放大等问题。然而，在高土石坝混凝土防渗墙的破损分析中，局部破损计算采用非局部PD 模型，虽然该局部区域可以选取得非常小，但在三维情形下，矩阵的稀疏性大大削弱，计算量陡增，面对实际复杂工程仍然是无能为力的。因此，此时并发式多尺度方法不再适用，有必要发展基于均匀化多尺度方法的等效简化分析模型，这种简化模型既能保留前期多尺度分析获得的某些破损信息，又能较为简单地为工程大尺度计算服务，这样就能更好地将多尺度方法应用于实际工程。

多尺度分析方法根据分析对象或问题的不同可大致划分为两类：均匀化递阶式方法和并发式方法［19］。针对不同的问题，应根据两类方法的特点合理地加以选择。本文采用均匀化多尺度方法（Homogenization/Hierarchical multiscale method）沟通宏细观信息，建立可包含细观破损演化信息在内的宏观损伤模型。Fish 等［20-22］采用双尺度渐进展开法研究复合材料的破损，通过引入某些假设，缩减单胞RVE 的自由度，发展了一种降阶多尺度方法（Reduced order multiscale method），其可根据分析问题的特点，引入某些假设，缩减单胞的自由度，这样耦合计算量即大为减少。Ghosh［23-24］研究提出了另外一种简化多尺度方法的思路，在细观上采用VCFEM（Voronoi cell finite element method）模拟复合材料破损，均匀化后得到宏观上的各向同性或各向异性的损伤模型，直接使用该模型进行宏观破损分析。这种宏观损伤模型，被称为均匀化损伤模型（Homogenization-based continuum damage model）。在土木工程中，也有学者对多尺度等效分析模型进行了研究。Zhang［25］根据复杂模型和简化模型动力模式等效来进行等效简化模型的参数识别，发展了桥梁隧道工程中大型正交各向异性结构的等效简化建模方法。梁诗雪等［26］通过多尺度均匀化方法，对含有缺陷的混凝土细观RVE（Representative volume element）进行随机分析，得到了工程实用的混凝土随机损伤演化方程。李阳［27］根据均匀化多尺度方法得到的刚度矩阵具有各向异性的特点，假设碎石桩复合地基为横观各向同性材料，据此推导了碎石桩复合地基等效简化模型，并给出了等效模型参数的取值方法。

本文借鉴Ghosh 建立均匀化损伤模型的方法，采用近场动力学多尺度均匀化方法，建立一种包含破损演化信息在内的等效损伤模型，以供高土石坝工程三维分析使用。

1 近场动力学基本理论

近场动力学（Peridynamics，PD）理论［14］是一种非局部计算力学理论。这种理论基于积分-微分方程，是对一般用偏微分方程描述的经典连续介质力学理论的一次重大改进，避免了位移导数项，获得了连续-非连续的统一表达，可直接采用键的断裂（bond breakage）来模拟裂缝扩展。它在描述复杂破损问题方面具有巨大的优势，从而可方便地分析防渗墙混凝土结构的破损问题。采用非常规态型（non-ordinary state-based）PD理论［15］，该理论不再使用键的刚度来与连续介质力学模型等效，而是可以直接嵌入已有的连续介质力学中的本构模型，工程应用较为方便。

NOSBPD的运动方程［15］为

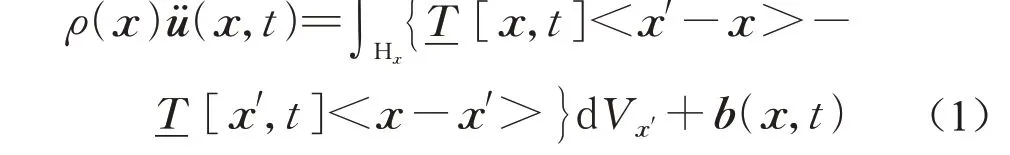
式中：ρ为质量密度；u为位移；b为给定的体积力；t为时间；Hx为点x的邻域，它是指初始参考构型中截断半径δ所包围的区域；f为对点力函数；-T[x，t]＜x′-x＞--T[x′，t]＜x-x′＞表示作用在点x上的由点x′给的力密度向量；-T[x，t]和-T[x'，t]为力向量态。

初始位置参考构形向量态和某一时刻的变形向量态分别为

式（6）建立了NOSBPD中的力态与经典连续介质力学理论中的应力、变形梯度（或应变）等物理量之间的关系。即PD 键发生变形后，通过式（4）可以计算出非局部变形梯度（也可以得到应变），通过材料本构可以得到应力。将变形梯度（或应变）与应力代入式（6），即可得到PD 的力态，从而代入式（1），进行PD运动方程的计算。同时，材料损伤准则体现在影响函数ω(‖ξ‖)中。

2 等效损伤模型建立的基本原理

2.1 总体思路

在采用精细化PD-FEM耦合方法分析防渗墙破损时，随着PD 键的逐渐断裂，破损区材料性能不断退化。根据上述NOSBPD方法的基本原理可知，材料在受载过程中键的断裂对结构的作用是通过影响函数来体现的，而影响函数的值又会影响到变形梯度的计算（见式（4）），进而可认为影响到应变的计算，故可将应力表达为

即此时d=0.5。

图2 破损区某PD点邻域内键的状态示意图Fig.2 Damage status of the bonds in the horizon of a peridynamics material point located in the damage zone

因此，精细化PD-FEM耦合分析时，防渗墙破损模拟是通过改造“形函数”来实现的，即某点邻域内的键，如果达到阈值，可以进行删除，这就相当于具有了丰富的“形函数”，可以表达多种变形模式（这与XFEM引入非连续变形的变形模式是类似的），同时键是有方向的，这就使得其依靠单个键的破损准则即能够模拟裂缝的走向，而无需再借助于其他判别标准。而对于基于有限元离散的经典连续介质力学理论，单元内部的变形模式是连续的，不具有表达非连续变形的能力，但可以用损伤变量来表达材料受荷过程中的性能衰退，达到模拟材料破损的目的，即可将式（7）改写成

所以，首先可通过式（7）表达的PD-FEM耦合分析确定在给定应力路径下混凝土防渗墙破损过程，从而得到损伤变量d的演化规律，再代入到式（9）中，即可得到与该精细化方法相等效的简化分析模型。

由精细化PD-FEM 耦合分析可知，防渗墙结构的破损是一定应力状态下发生的复杂的材料性能退化过程。同时，防渗墙在特定应力路径下存在拉、压2种破损模式。因此，本文在对防渗墙破损应力路径进行分析和简化后，使用多尺度均匀化方法分析RVE拉压损伤演化过程，最终建立形式简单的损伤模型。

2.2 应力路径分析

（1）受拉破损模式。基于某堰塞坝防渗墙破损的PD-FEM 耦合分析［17］，研究防渗墙在受拉破损模式下的应力路径。该破损模式控制工况在蓄水期。蓄水过程中防渗墙破损区典型点应力路径如图3a所示。防渗墙施工完成后，水位较低时，存在着一定的卸载过程，而后随着墙前水位逐步淹没该点，防渗墙受到的围压和弯矩引起的拉应力同步增大，轴向从受压逐步过渡到受拉状态，最后在拉剪耦合应力作用下发生破损。根据破损区应力状态的分析［13］，确定破损区围压σ1为0～2.0MPa。

（2）受压破损模式。基于某砾石土心墙堆石坝覆盖层坝基防渗墙破损的多尺度分析［13］，研究防渗墙在受压破损模式下的应力路径。该破损模式控制工况在施工期。有研究表明，土石坝填筑过程是一个坝体大小主应力增量比基本不变、各主应力逐渐增大的等应力比加载过程［28］。防渗墙破损区典型点的应力路径如图3b所示。分析可知，在坝体填筑过程中，墙体的应力路径也基本符合等应力比加载的特点，随着大主应力的持续增大，墙体发生受压破损。根据破损区应力状态的分析［13］，确定破损区围压σ3为0～2.0MPa。

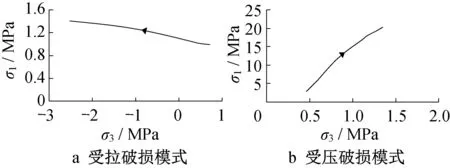
图3 防渗墙应力路径（仅显示了破损时刻附近）Fig.3 Stress path of cut-off wall (only near thedamage instance is shown)

2.3 均匀化过程

首先取RVE，根据防渗墙破损应力路径的分析，施加相应的拉压和压压混合荷载（图4），同时为了引起不均匀破损，在RVE 中引入了随机缺陷，采用PD分析该RVE破损过程。在PD模型中，采用的是基于能量的键的断裂准则［17］。

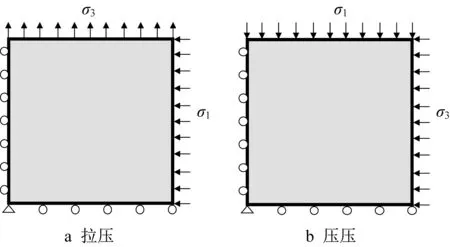
图4 细观RVE及其边界条件Fig.4 RVE and its boundary conditions

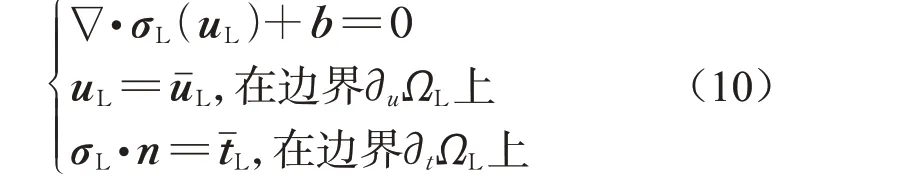
这样，得到RVE的控制方程为式中：下标L 表示与RVE 有关的量。破损信息由PD表达。

对由式（10）获得的应力场σ和应变场ε（注意这里的非局部应变应是所有键都完好情形下计算出来的，即后处理时，对于断裂的键，应将其恢复为完整的键再进行应变计算）进行均匀化，如式（11）、（12）：

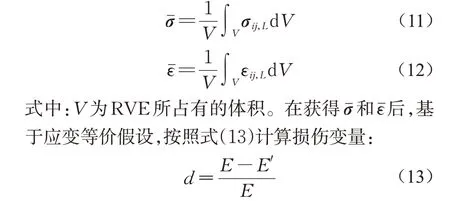
式中：d为损伤变量；E为无损时的弹性模量；E′为损伤后的弹性模量。

PD方法可以自发地判断裂缝走向，因此得到的损伤应是各向异性的张量，但这里简单地通过一个标量d来定义损伤。即通过多尺度均匀化分析得到损伤因子d与总应变ε的关系，从而建立包含破损信息在内的宏观各向同性损伤模型。

得到损伤变量的演化规律后，即可采用经典连续介质力学理论描述宏观尺度，并采用常规有限元方法进行离散。这样，得到总的宏观控制方程为

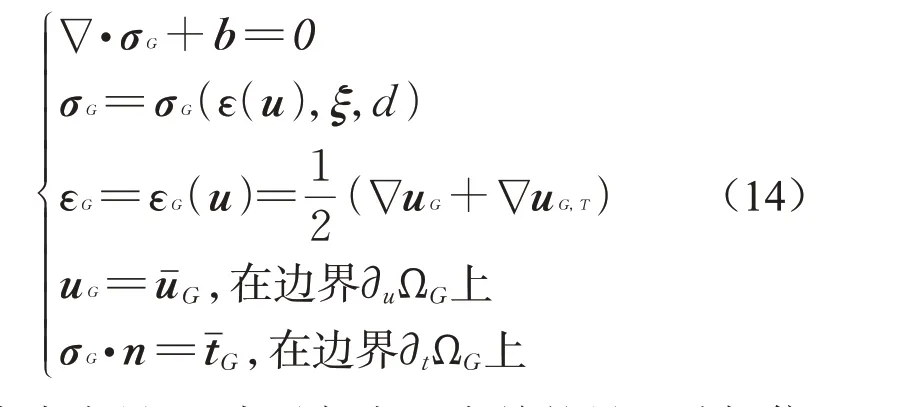
式中：ξ为内变量；G表示与宏观有关的量。破损信息由损伤变量d表达。

3 等效损伤模型

3.1 损伤演化规律

对于普通混凝土防渗墙，按照泵送浇筑的要求，一般采用二级配混凝土，参考水工混凝土试验规程对于二级配混凝土试样尺寸的规定，选取RVE大小为150mm×150mm。混凝土变形破损计算参数如表1所示。

表1 防渗墙RVE变形破损计算参数Tab.1 Computational parameters for the concrete cut-off wall

（1）受拉破损模式。根据前面应力路径的分析，这里研究σ1为0、1、2MPa 不同围压情形下防渗墙RVE 在拉压荷载作用下的破损规律。边界条件如图4a所示。最终得到不同围压下，承受拉压荷载作用的防渗墙RVE 的损伤曲线如图5a 所示。由分析可知，由于副轴方向压应力与抗压强度的比值比较小，破坏仍主要由主轴方向的拉应力控制，因此围压的增大对峰值强度和损伤曲线的影响较小。同时，损伤曲线均大致呈现外凸形状，即在损伤值0.8 之前，损伤发展较快，在其之后则发展较慢，逐步趋近于完全损伤。

（2）受压破损模式。根据前面应力路径的分析，这里研究σ3为0、1、2MPa 不同围压情形下防渗墙RVE 在压压荷载作用下的破损规律。边界条件如图4b所示。最终得到不同围压下，承受压压荷载作用的防渗墙RVE 损伤曲线如图5b 所示。由分析可知，由于副轴/主轴应力比较小，所以围压对受压损伤发展影响比较小（特别是在损伤发展较快的初始阶段），并且仍然具有在损伤值小于0.8的曲线段发展较快而后发展趋缓的特点。

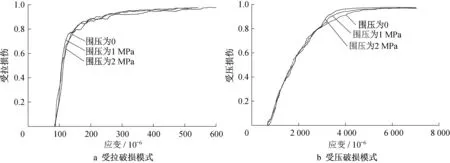
图5 不同围压荷载作用下RVE损伤曲线Fig.5 Damage curves at different confining pressure loads of the RVE

3.2 拉压统一损伤模型

由前面的分析可知，在防渗墙破损对应的应力路径下，围压对受拉和受压损伤发展的影响较小，同时受拉和受压损伤曲线均具有指数型的发展形式，因此这里以单轴受拉和单轴受压破损过程为研究对象，参考两类形式比较简单混凝土静动力损伤模型即双线性模型［29］和指数型模型［30］后，考虑多尺度均匀化得到的受拉和受压损伤曲线的特点，建立了如式（15）形式简单的拉压统一损伤模型：

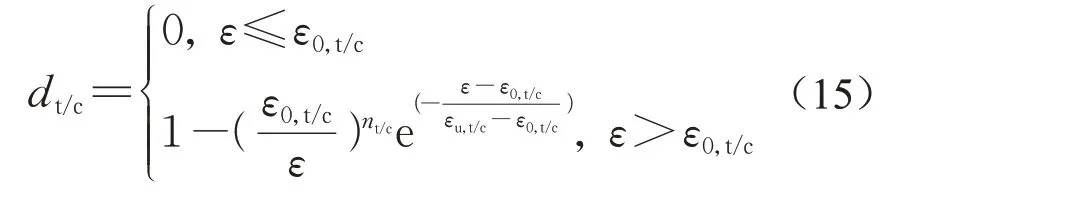
式中：ε为应变；ε0，t/c为损伤门槛应变；εu，t/c为接近完全损伤对应的应变；nt/c为本文添加的参数，用来控制损伤发展的快慢。

使用式（15）拟合损伤曲线，受拉损伤取ε0，t=6.67×10-5，εu，t=1×10-3，nt=2.5，受 压 损 伤 取ε0，c=6.67×10-4，εu，c=1×10-2，nc=0.8。由图6可知：本文模型可以通过调节参数nt/c来模拟相应的损伤发展速度，对受拉损伤模拟较好，而双线性模型是假设应力应变软化段为直线型而得到的简化损伤模型，其和指数型模型都有可能会低估混凝土损伤发展速度。为了使模型形式简单且参数少，本文没有对受压损伤进行更精细的描述，因此模型对受压损伤模拟有一定的偏差，但选择合适的参数后，模型总体上仍能近似模拟曲线的大致形状和演化过程。

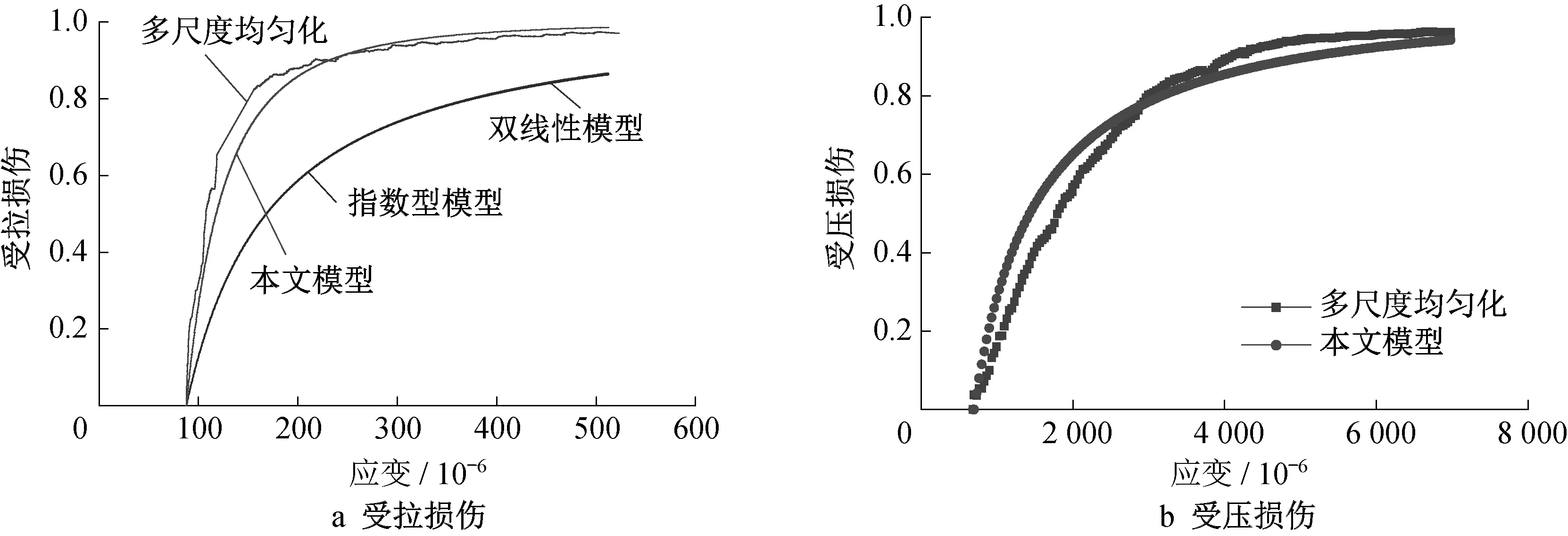
图6 损伤因子演化规律拟合结果Fig.6 Fitting results of evolution laws of damage factors

3.3 模型参数的确定

模 型 拉 压 损 伤dt/c各 具 有3 个 参 数：ε0，t/c、εu，t/c和nt/c。

（1）ε0，t/c为损伤门槛应变。这里与Mazars 模型［31］一样，假设峰值前无损伤，近似取ε0，t=ft/E0和ε0，c=fc/E0，其中ft为单轴抗拉强度，fc为单轴抗压强度，E0为初始弹性模量。ε0，t/c可通过混凝土抗拉和抗压强度试验确定。

（2）εu，t/c为接近完全损伤时的应变。它们可取为混凝土极限拉压应变，并可通过混凝土极限拉伸和混凝土柱承压试验确定。定义极限应变系数η=εu，t/c/ε0，t/c，若无试验数据，η可取10左右。

（3）nt/c为控制损伤发展快慢的参数。nt/c取值越大，则损伤越快。nt/c可通过试验测定混凝土单轴受拉或受压应力应变全曲线，按照式（13）计算损伤值dt/c，然后根据试验测点进行确定。假设有试验测点(ε1，t/c，d1，t/c)，其中d1，t/c≠0，d1，t/c≠1，则

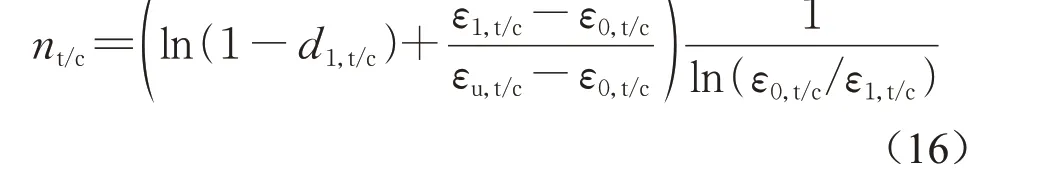
在实际操作中，可选取多对试验点，最后取平均值加以确定nt/c值，甚至还可以在曲线的不同阶段选取各自的测点，从而确定各自不同的nt/c，这样可以更好地与试验曲线相匹配。若无试验数据，对于常见的刚性混凝土防渗墙，通过相应的多尺度均匀化计算分析，建议nt取2.5，而nc取0.8。

4 模型的验证

4.1 混凝土单轴试验

首先采用文献中的材料试验［32］验证本文损伤模型模拟混凝土单轴受拉和受压应力-应变曲线及其损伤发展过程的有效性。混凝土材料参数为：E=31GPa，ft=3.48MPa，fc=27.6MPa。损伤模型参数根据试验数据确定为：ε0，t=1.12×10-4，εu，t=1×10-3，nt=2.5 和ε0，c=8.90×10-4，εu，c=8×10-3，nc=0.8。模型模拟效果如图7和图8所示，其中试验损伤值是根据试验数据采用式（13）计算而得到的。

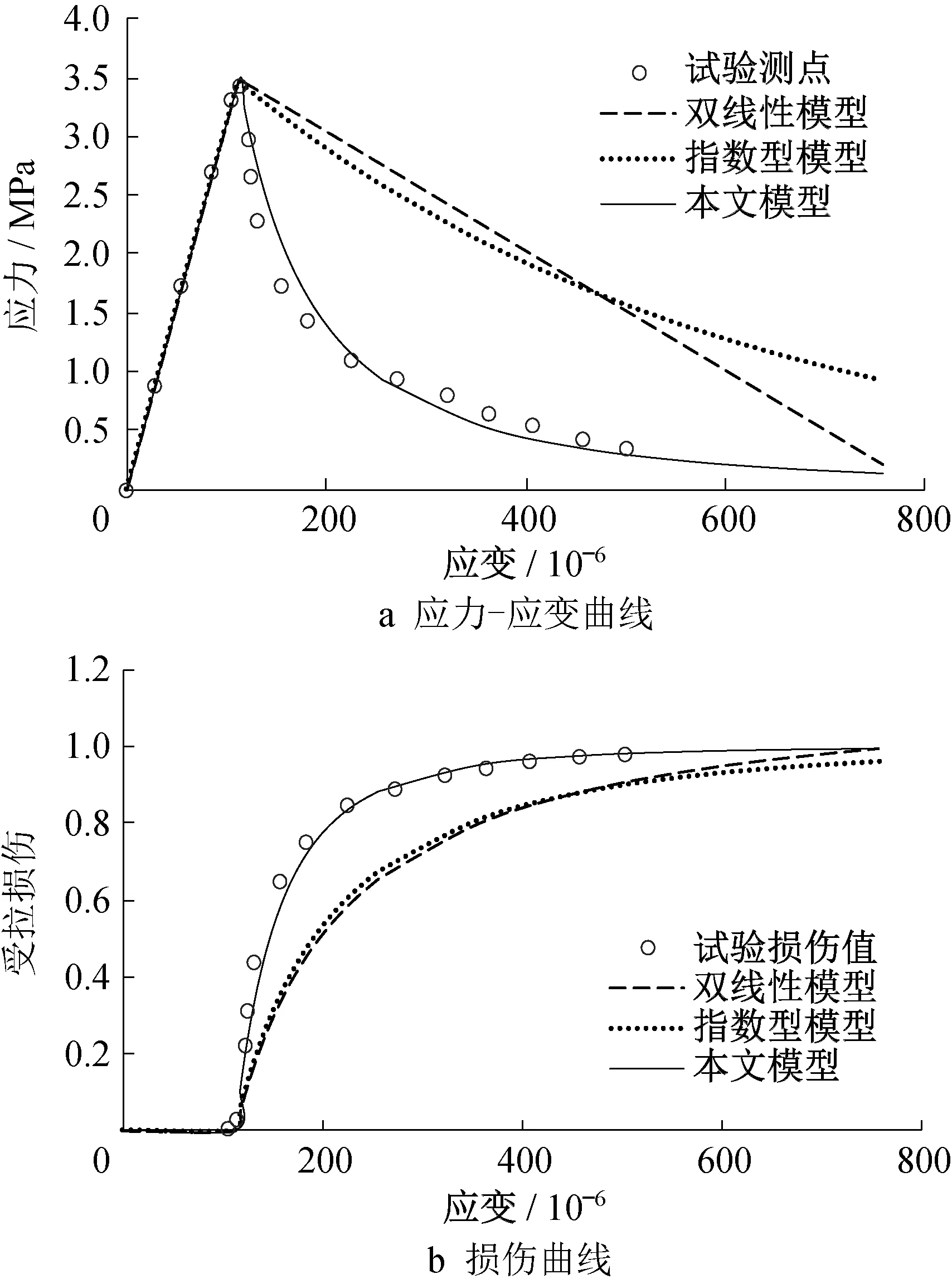
图7 混凝土单轴受拉模拟Fig.7 Simulation results of uniaxial tension test of concrete

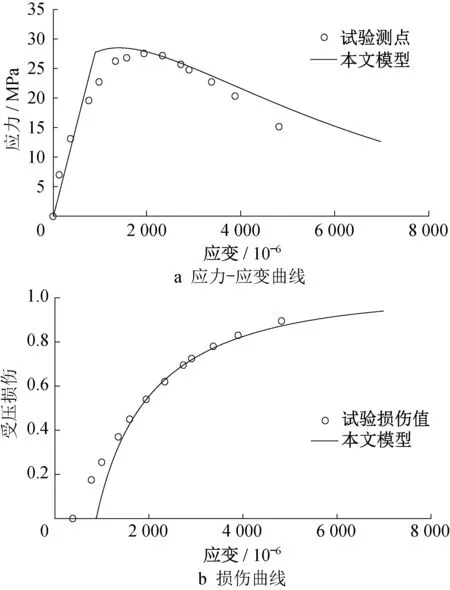
图8 混凝土单轴受压模拟Fig.8 Simulation results of uniaxial compression test of concrete

模拟结果表明，对于混凝土单轴受拉，本文模型模拟效果较好，而双线性模型（εu，t=8×10-4）和指数型模型（εu，t=6×10-4，nt=1.0）则低估了损伤发展速度，模拟效果不佳；对于混凝土单轴受压，本文模型假设峰值前无损伤，这导致模拟结果与试验值存在一定的偏差，更精确地模拟可以考虑调整混凝土受压损伤门槛值，但这可能需要更多的模型参数，不便于工程应用。

总体上来说，本文模型新引入了指数参数nt/c，相比于指数型或双线性模型，可较好地模拟混凝土材料单轴受拉损伤发展过程，同时也可近似地模拟混凝土材料单轴受压损伤发展过程。

4.2 偏心三点弯曲梁

采用混凝土偏心三点弯曲梁［33］算例来验证等效模型在混凝土结构破损模拟方面的有效性。混凝土计 算 参 数 为：E=38GPa，υ=0.2，ft=3.0MPa，GI=69N·m-1，损 伤 模 型 参 数 为：ε0，t=7.89×10-5，εu，t=1×10-3，nt=2.5（需要根据有限元单元尺寸大小，进行相应的正则化，以保持断裂能的恒定［34］）。PD-FEM 耦合模型中PD 的离散参数为：Δx=1mm，δ=3Δx。

图9为试验布置和几何尺寸。图10为2种方法的计算模型。图11 为最终裂缝形态。图12 为2 种方法得到的加载点承载力-位移曲线与试验测值的比较，灰色带阴影部分为试验测得的包络线。由分析可知，在破损分布方面，损伤模型计算的损伤区域由于弥散效应，相比多尺度或者试验结果，稍微偏大；在承载力位移曲线方面，峰值及峰后行为基本都在试验测得的包络区间内，吻合较好。

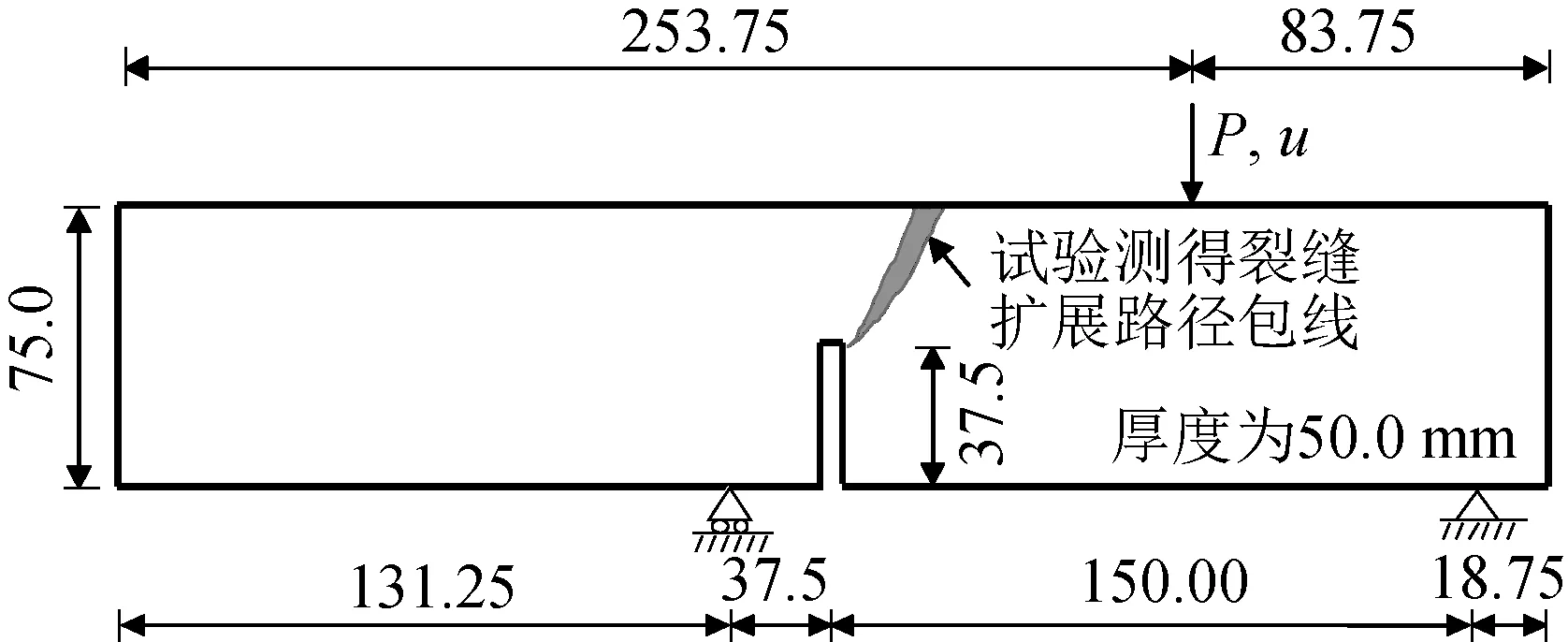
图9 混凝土偏心三点弯曲梁试验（单位：mm）Fig.9 Concrete eccentric three-point bending beam test(unit:mm)

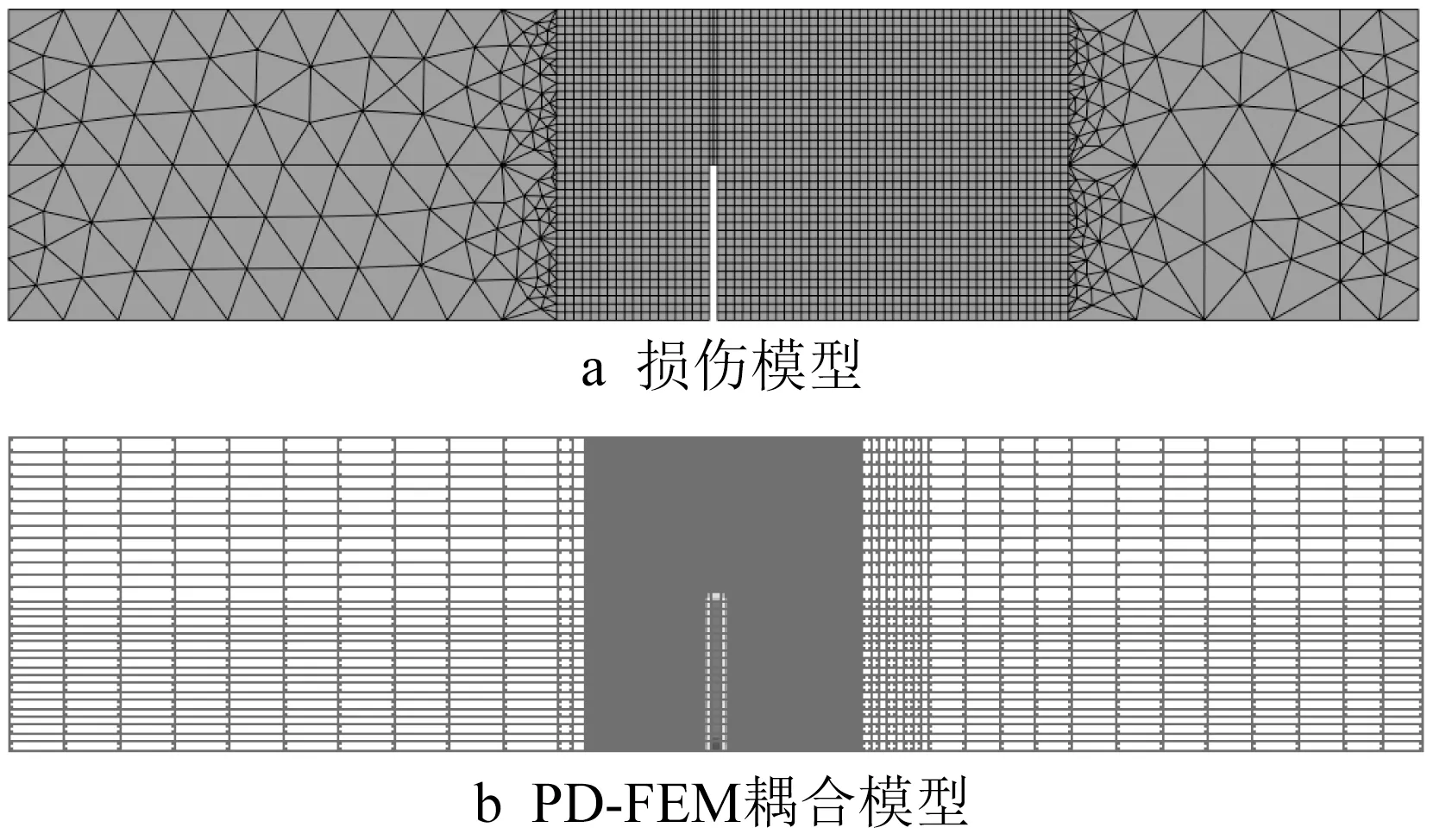
图10 计算模型Fig.10 Computational models for different methods

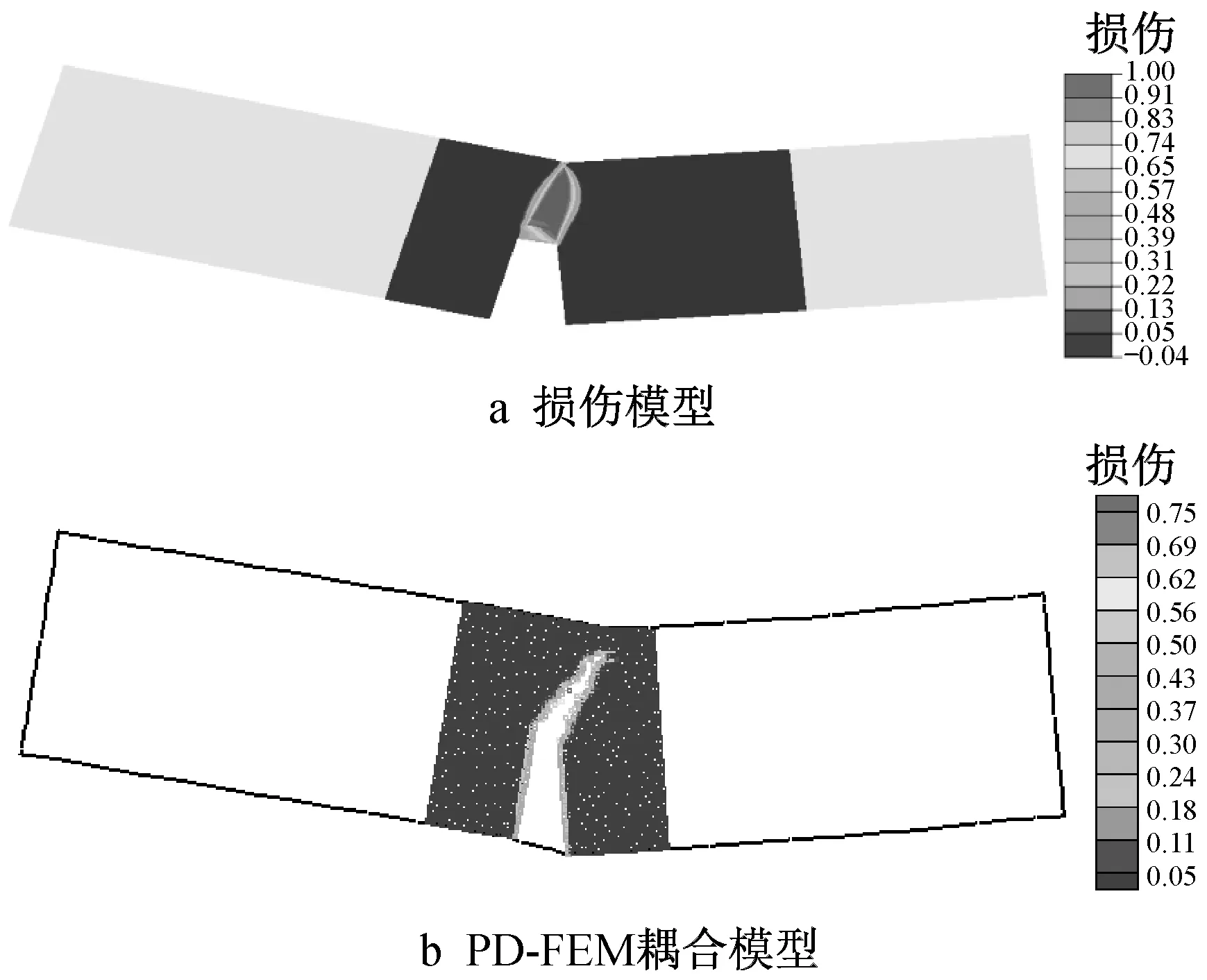
图11 变形放大100倍时的最终裂缝形态Fig.11 Final crack patterns (at a deformation magnification factor of 100)

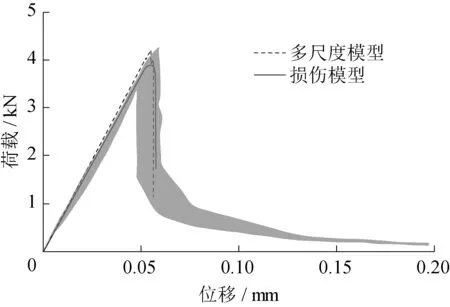
图12 加载点荷载-位移曲线Fig.12 Curves of bearing capacities versus displacements

因此，本文建立的等效模型可以在避免多尺度复杂计算的前提下获得较好的混凝土结构破损模拟效果。

5 模型的工程应用

以某砾石土心墙堆石坝为工程背景，并进行一定的简化，使用本文等效模型进行该堆石坝防渗墙三维破损分析。该心墙堆石坝坝高123m，河床覆盖层（最大厚度72.4m）设置一道厚度为1.2m 的全封闭式混凝土防渗墙防渗［35］。计算模型如图13所示。计算参数［36］如表2 所列。另外，防渗墙损伤模型参数取自图6。

表2 计算参数Tab.2 Computational parameters

图14给出了基于等效损伤模型的墙体位移、应力和损伤分布。由分析可知，等效模型能够有效地模拟高土石坝坝基防渗墙的三维破损状况，其中受拉损伤主要分布在防渗墙顶部扩大端和防渗墙两岸岸坡约束区域，而河床中下部区域则出现较大范围的受压损伤。

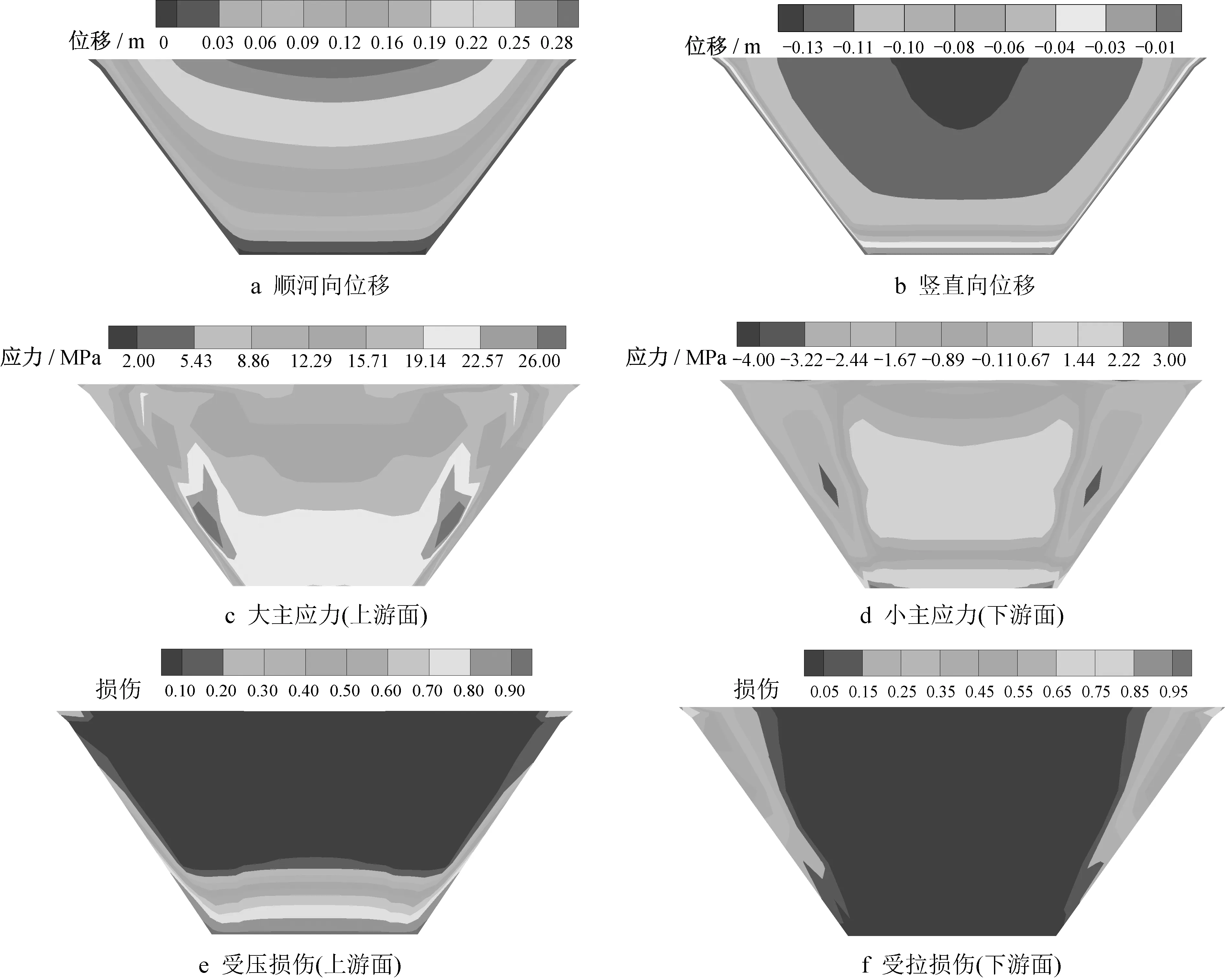
图14 基于等效损伤模型的墙体位移、应力和损伤分布Fig.14 Distributions of displacements,stress,and damage of cut-off wall using the method proposed

6 结语

基于防渗墙破损的机理和应力状态规律的认识，采用近场动力学多尺度均匀化方法，建立了可用于工程三维分析的高土石坝防渗墙破损的等效模型，最后完成了模型的验证和工程应用。同时，该等效损伤模型建立的思路也可供其他类似工程参考。

近场动力学多尺度均匀化方法建立的拉压统一损伤模型，形式简单、参数少且具有明确的物理意义。模型新引入了指数参数nt/c，相比于指数型或双线性模型，可以更好地模拟混凝土材料单轴受拉损伤发展过程，同时也可近似地模拟单轴受压损伤发展过程。采用偏心三点弯曲梁算例验证了等效模型可以在避免多尺度复杂计算的前提下获得较好的混凝土结构破损模拟效果，破损分布和结构承载力曲线计算结果与试验或多尺度方法较为一致。采用该模型进行了某砾石土心墙堆石坝工程的三维计算分析，结果表明建立的等效模型能够有效地模拟高土石坝坝基防渗墙的三维破损状况，其中受拉损伤主要分布在防渗墙顶部扩大端和防渗墙两岸岸坡约束区域，而河床中下部区域则出现较大范围的受压损伤。

作者贡献声明：

孙 伟：完成论文主要计算和分析工作，撰写论文。

包世诚：整理论文初稿。

张 嘎：提出选题，设计论文框架。