铝合金板式节点火灾后承载性能

郭小农，徐泽宇，陈 晨，罗金辉

（1. 同济大学土木工程学院，上海 200092；2. 华润置地有限公司，上海 201103）

板式节点是铝合金单层网壳结构中最为常见的节点形式［1-3］。其优点在于造型美观、施工方便；该节点采用了紧固件连接而非焊接，可避免焊接引起的铝合金材料强度的折减。目前，对常温下铝合金板式节点力学性能的研究已较为深入。研究结果表明铝合金板式节点的破坏模式主要为节点板块状拉剪破坏和节点板的屈曲破坏［4-6］，其受力全过程符合四折线模型［7］，当构件为箱型截面时还易发生构件端部的撕裂破坏［8-9］。在往复荷载作用下，铝合金板式节点由于其受力初期会发生螺栓滑移，节点耗能能力较差［10］。

对铝合金板式节点高温下性能的研究相对较少，郭小农团队曾对高温下铝合金板式节点平面外受弯承载力进行试验研究［11］，发现节点在高温下的破坏模式与常温下一致，且当节点板厚度较大时，节点域在300℃以下不会发生破坏；在进行铝合金板式节点网壳破坏性火灾试验时，发现网壳在火灾下的破坏模式为倒塌破坏，结构部件的破坏模式包括熔化、断裂和弯扭失稳破坏，在进行结构设计时需考虑温度场的不均匀分布［12］。

在许多空间钢结构的火灾事故中，结构在遭遇火灾后仅出现局部损伤，一般不会发生整体垮塌，较为典型的案例如济南奥体中心网壳［13］。铝合金结构也存在同样的情况，虽然铝合金在高温下的力学性能较差［14］，但在火灾发生后，其强度会随着外界温度的降低而得到不同程度的恢复，使得灾后未倒塌结构仍具备一定承载能力，经检测和修复加固后仍可继续使用，从而降低火灾损失。

节点作为结构中受力最为关键的部分，其火灾后的承载性能值得关注；但目前尚未出现有关铝合金板式节点火灾后力学性能的研究。基于此，通过试验及有限元分析，对铝合金板式节点火灾后承载性能进行研究，以便为铝合金网壳的火灾后修复加固提供依据。

1 材性试验

所有材性试样均在截面规格为H100mm×50mm×4mm×5mm 的6061-T6 铝合金杆件腹板处取样，材性试件的尺寸按GB/T 228—2010［15］以及GB/T 2975—2018［16］标准确定。将材性试件在高温炉中加热以模拟试件的过火过程，按ISO834标准升温曲线进行自动升温，当炉温达预设过火温度后，恒温0.5h后取出并自然冷却至室温，用于材料力学性能试验［17-21］。过火温度Taf分别为室温（20℃）、100℃、200℃、300℃、350℃、400℃、450℃、500℃和550℃等，每个温度下各有2 根拉伸试件，试件总数为18 根。试件按“CG-T-i”进行命名，其中T表示过火温度，i表示平行试件编号。

18 根标准材性试件破坏形态如图1a 所示。当过火温度低于300℃时，材性试件断裂处有明显颈缩现象，具备塑性破坏特征；当过火温度处于300～450℃时，材性试件主要发生脆性破坏，断裂处未表现出明显的颈缩，从试件的应力-应变曲线（图1b）也可以看出，此时试件的极限应变显著减小；而当过火温度高于450℃时，材性试件断裂处也有明显颈缩现象，并重新具备塑性破坏特征，试件的极限应变增大。

表1给出了9组拉伸试验的试验结果，表中数据为2根平行试件的平均值。由表1可见，过火温度对铝合金弹性模量的影响很小，经不同温度过火后，试件的弹性模量与常温时基本一致，其平均弹性模量为69.8GPa。

表1 拉伸试验结果Tab.1 Tensile test results

由于国产6061-T6铝合金的应力-应变关系曲线没有明显的屈服平台，其名义屈服强度取残余应变为0.2%对应的应力f0.2。当过火温度低于300℃时，其屈服强度及抗拉强度与常温状态下基本一致；当过火温度高于300℃后，屈服强度及抗拉强度开始迅速减小，并在450℃时达到最低值；而当过火温度高于450℃后，屈服强度及抗拉强度又会有较小幅度的提升。

定义铝合金屈服强度折减系数为过火后的屈服强度fyT与室温下未受火的屈服强度fy之比，抗拉强度过火折减系数为受火后的抗拉强度fuT与室温下未受火的抗拉强度fu之比。基于试验结果计算得到的屈服强度及抗拉强度过火折减系数变化规律呈现明显的“三折线”走势，最终拟合得到的强度过火折减系数计算式为见式（1）和式（2）。试验和拟合计算式得到的强度过火折减系数对比如图2所示。

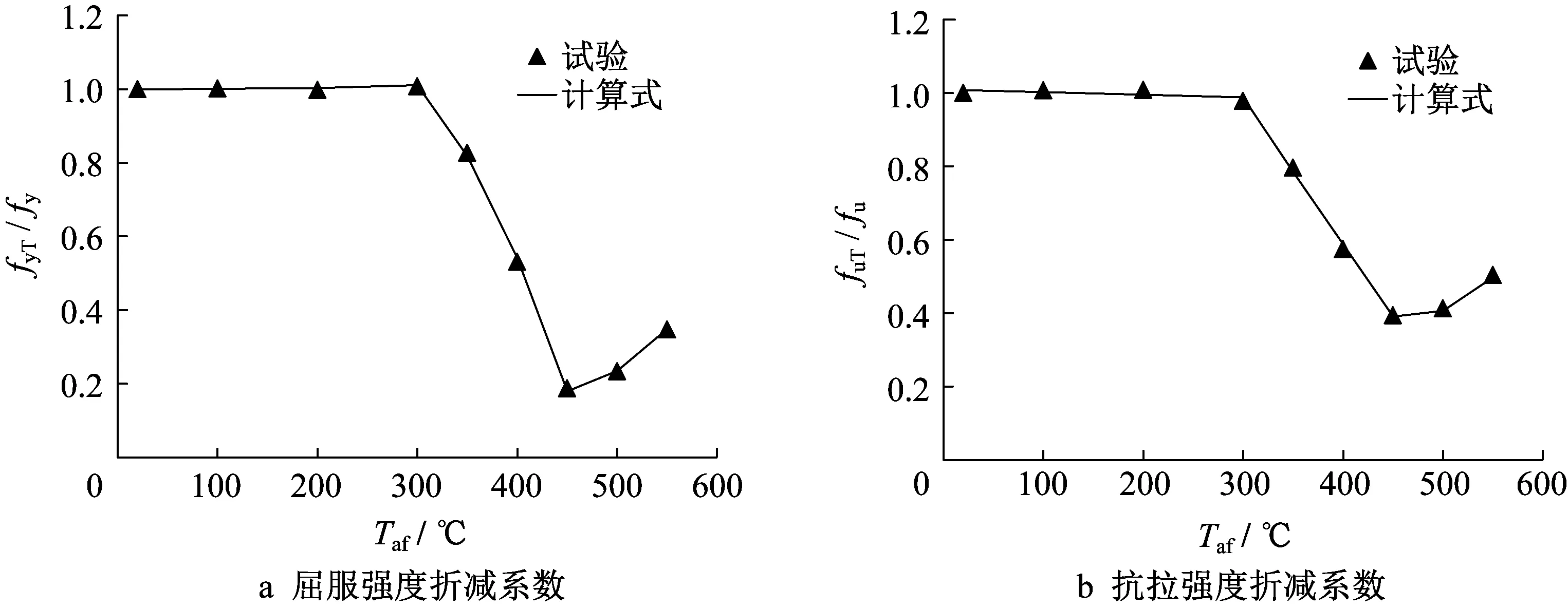
图2 强度折减系数Fig.2 Strength reduction factors

2 节点试验

2.1 试件设计

为研究过火温度和节点板厚度对铝合金板式节点承载力和刚度的影响，考虑过火温度为室温（20℃）、200℃、300℃、400℃、500℃和550℃等6 种情况，节点各部件过火过程与材性试件过火过程一致，节点板厚度为2mm和5mm这2种情况，共计12个板式节点试件。节点试件按“JT-j”进行命名，其中T为过火温度，j为节点板的厚度。铝合金板式节点试件装配示意图如图3所示，节点板和杆件均为6061-T6铝合金。每个节点试件通过2 块节点板连接6 根H型杆件，其中4 根杆件长度为150mm，2 根杆件长度为1 050mm。杆件截面为工字型截面，取截面规格为H 100mm×50mm×4mm×5mm，根据郭小农团队以前的试验研究成果，该尺寸已能较好反应结构整体以及节点的受力特性［11-12］。每根杆件端部上、下翼缘通过6个M6不锈钢螺栓与节点板连接，螺孔直径均为6.5mm，螺栓材质为奥氏体不锈钢，性能等级为A2-70。

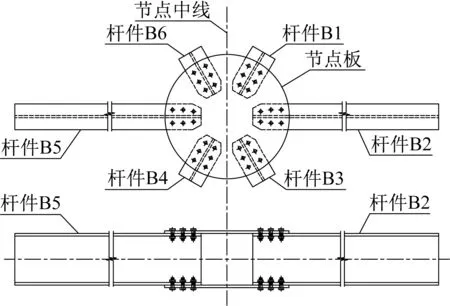
图3 板式节点试件示意Fig.3 Gusset plate joint specimens

2.2 加载方案

加载装置如图4a所示，采用两杆加载模式，节点域传力较为明确，便于研究节点域的受力机理以及破坏模式［22］。试验采用可调节宽度的夹支铰支座以模拟两端简支的约束支承条件，支座构造如图4b所示。试验采用两点对称加载，可防止因不平衡弯矩引起节点发生面外扭转，加载点与支座中心的水平距离为300mm。在每个千斤顶与加载杆件上翼缘之间各放置一块加载垫块以防止杆件局部压屈。

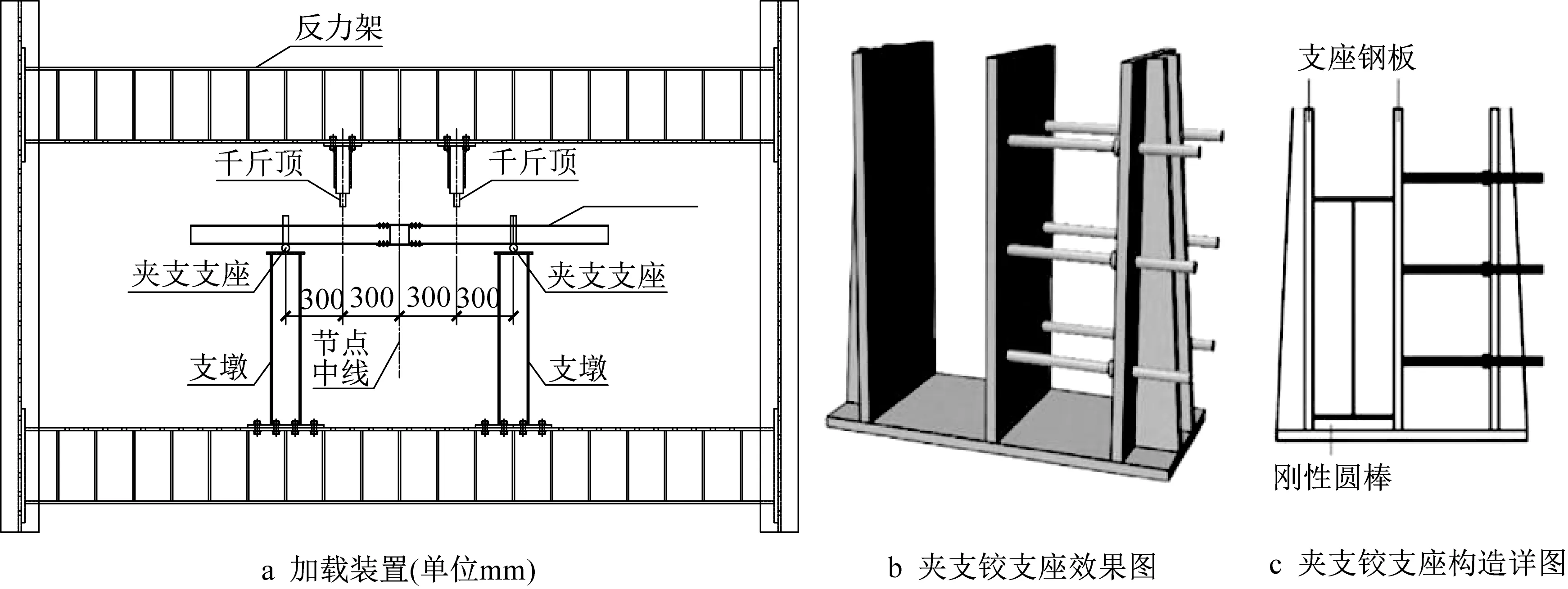
图4 加载方案示意Fig.4 Loading scheme

2.3 测点布置

所有试件采用相同的测点布置方案：分别在杆件B2、B5的加载点所在位置的下翼缘处布置一个位移计D-2、D-3 来监测加载点位移并测量杆件挠度，以此来间接计算节点的转角；为监测加载点是否出现面外偏心，分别在加载杆件B2、B5 靠近节点域的截面上、下翼缘的左右两端布置4枚单向应变片，编号为P5～P8、P9～P12，该处应变片读数可用于计算杆端弯矩和轴力；为监测约束端内力，分别在加载杆件B2、B5 靠近约束端的截面上、下翼缘的左右两侧布置4枚单向应变片，编号为P1～P4、P13～P16，杆件上的测点布置如图5所示。

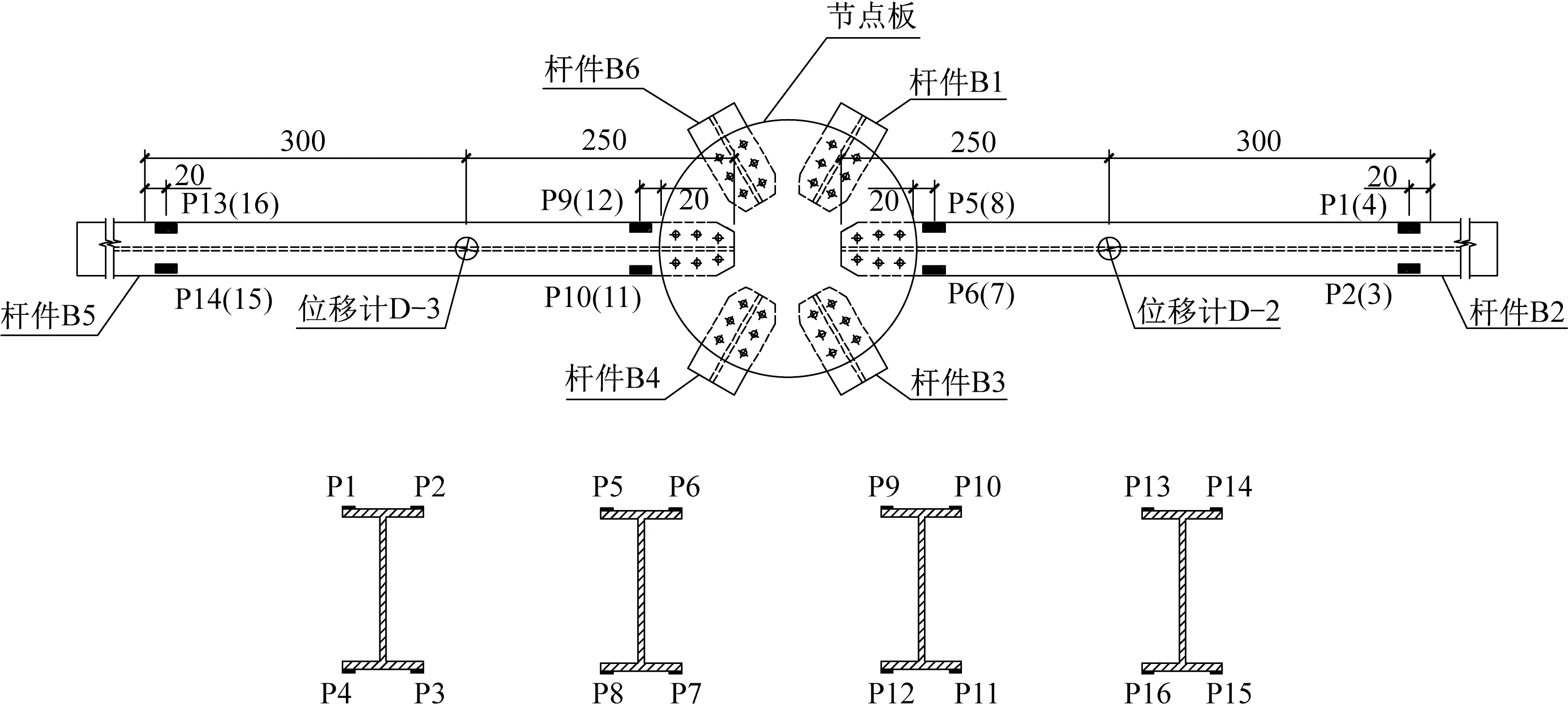
图5 杆件测点布置Fig.5 Arrangement of measuring points on members

在上节点板顶面及下节点板底面（外表面）自由区对称轴上布置3个径向和3个环向应变片，应变片按图6 中摆放情况进行顺时针编号；在上节点板顶面及下节点板底面（外表面）中心区对称轴上布置三向应变花；在上节点板外表面中心附近布置一竖向位移计D-1，用来监测节点试件的整体变形情况，节点板测点布置如图6所示。

3 节点试验结果及分析

3.1 破坏模式和承载力

第2节所述所有试件的破坏模式和极限承载力见表2。结合现场试验观察记录与实测曲线发现，在加载初期，螺栓与节点板首先开始贴紧，节点板此时发出轻微“噼啪”的响声，后续随着荷载的增加，杆件及节点板的竖向位移计及应变读数基本呈线性 增长。

表2 各试件的极限弯矩和破坏模式Tab.2 Bending capacity and failure modes of specimens

对于薄板节点，节点域向下移动的同时杆件并无明显变形而节点板则变形明显，最终节点板发生破坏，杆件无明显变形。薄板节点的节点板呈现块状拉剪破坏或屈曲破坏2种破坏形式，如图7a所示。对于厚板节点，节点板向下移动的同时向一侧倾斜，杆件出现弯扭变形。在加载末期，杆件发生明显弯扭变形，而节点板无明显变形。对于厚板节点只出现杆件失稳破坏，如图7b所示。

图7 试件破坏形态Fig.7 Failure modes of specimens

3.2 试验结果分析

根据实验监测系统记录的杆件上应变片读数，可得铝合金板式节点的弯矩-转角曲线［11］。常温下铝合金板式节点的弯曲刚度性能分为螺栓嵌固、螺栓滑移、孔壁承压和节点失效4 个阶段［10］，如图8所示。

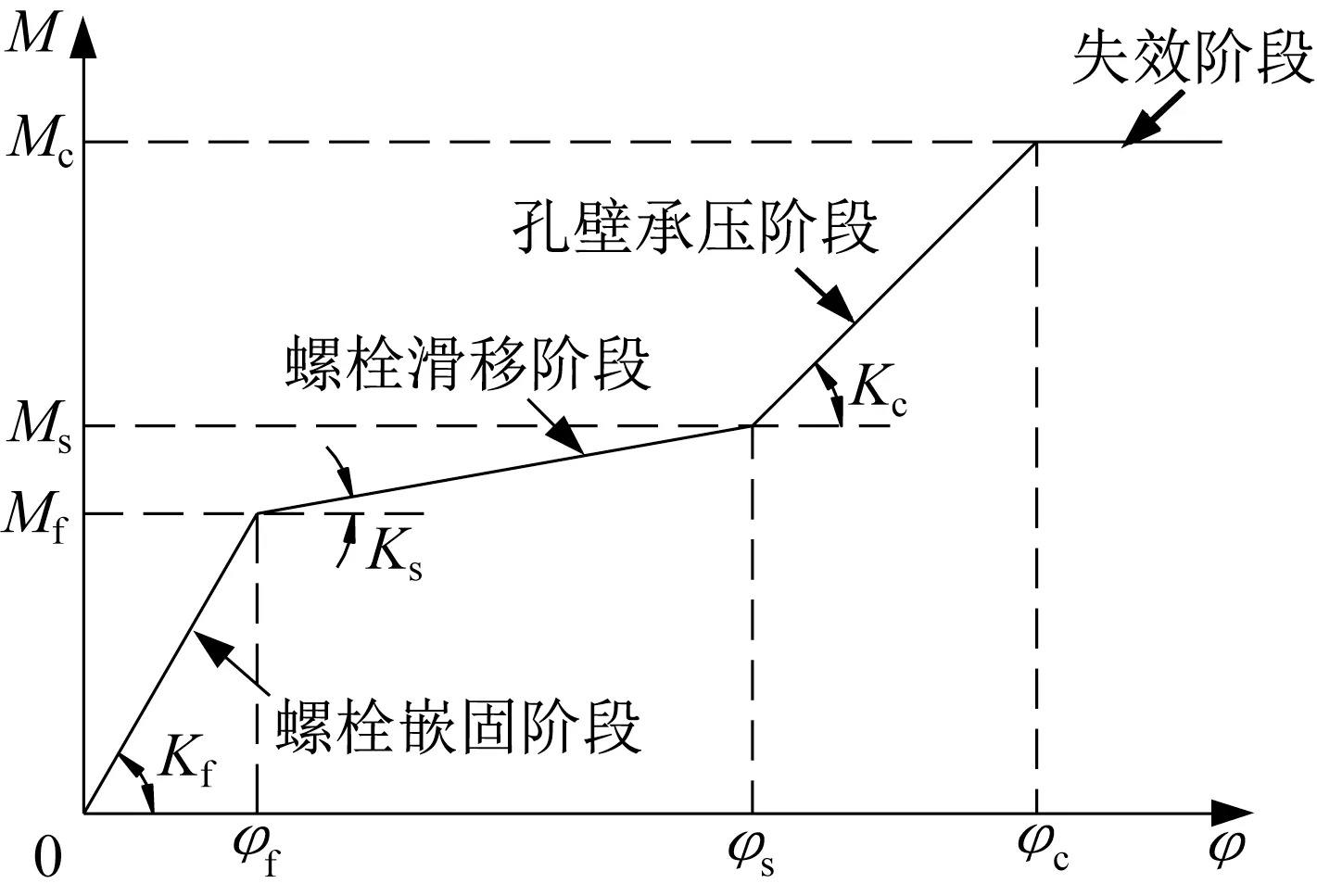
图8 铝合金板式节点四折线模型Fig.8 Four-line model of AAG joints

根据位移计D-1、D-2 和D-3 的读数，可以绘制出节点试件的弯矩-转角曲线，如图9 所示。由图9可知，过火后铝合金板式节点弯矩-转角曲线的形状基本符合常温下的四折线模型。图10 给出了各阶段刚度和承载力随过火温度的变化规律。

在加载初期，曲线进入螺栓嵌固阶段。从图9和图10 可以看出，随着过火温度的改变，螺栓嵌固阶段的刚度Kf及极限弯矩Mf并没有发生明显改变，螺栓滑移阶段的转角区间范围基本一致。由此可知，螺栓嵌固阶段极限弯矩Mf及刚度Kf基本没有折减，与过火温度无明显关系。

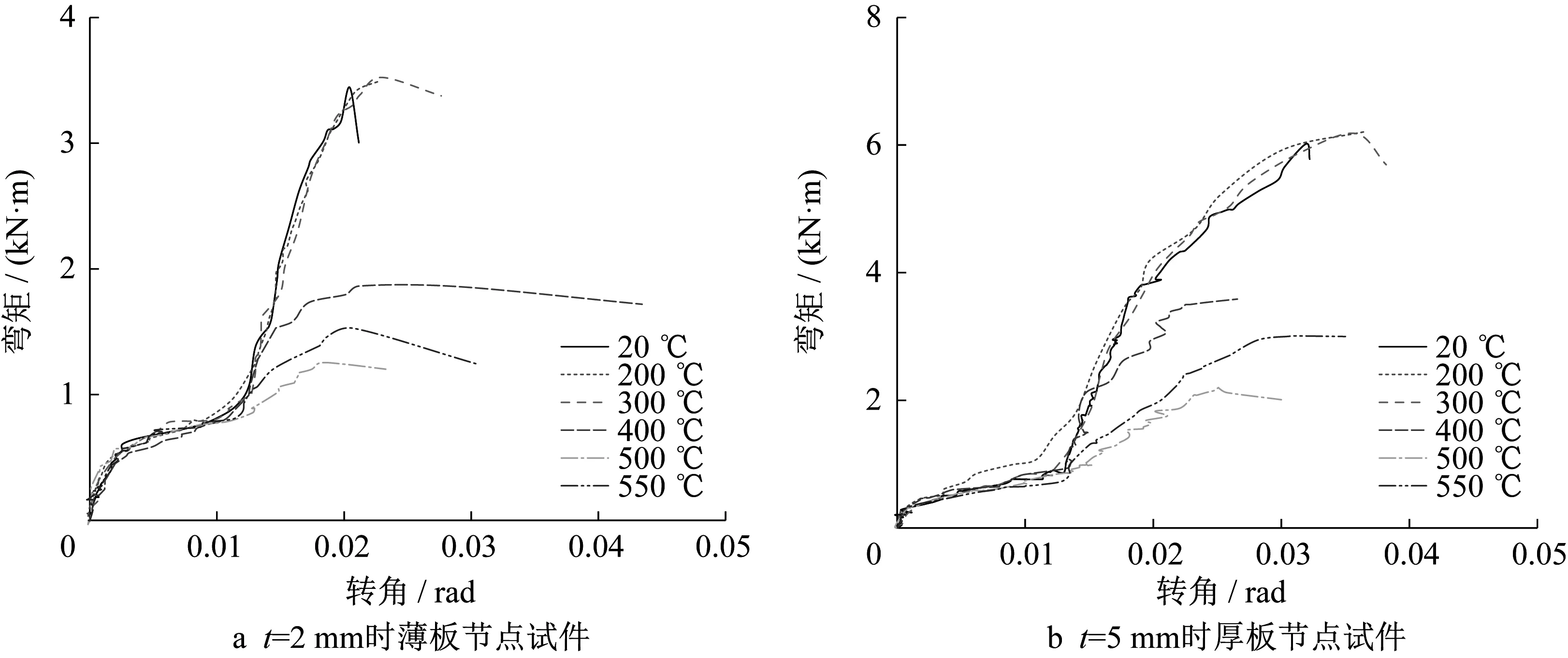
图9 弯矩-转角曲线Fig.9 Moment-rotation curves

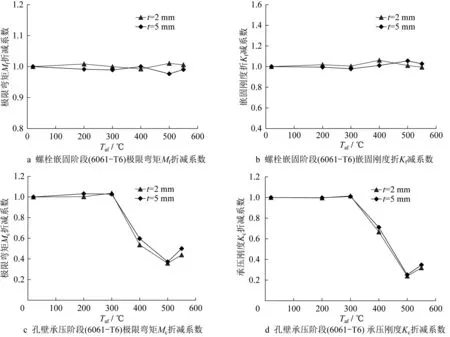
图10 过火后铝合金板式节点承载力和刚度折减系数Fig.10 Reduction factors of bearing capacity and stiffness of AAG joints after fire

在加载后期，曲线进入孔壁承压阶段，其刚度及极限弯矩随过火温度的改变发生不同程度的折减，图10c、图10d给出了铝合金板式节点过火后弯矩-转角曲线中孔壁承压阶段的极限弯矩Mc及刚度Kc与过火温度的关系。从图中可以初步得到，孔壁承压阶段的极限弯矩Mc及刚度Kc与过火温度的关系呈现“三折线”走势。

4 数值模拟的建立和验证

采用通用有限元软件ABAQUS 对过火后铝合金板式节点破坏过程进行模拟。考虑到螺栓对最终结果影响很小［11］，故数值模型中不对螺纹及垫片进行建模；螺杆直径采用其名义值，并考虑螺杆与螺栓孔之间的孔隙。为模拟部分螺栓与孔壁在正式加载前就进入了承压阶段这一现象，调整靠近节点中心的第1排螺孔直径与螺栓直径相同。两杆对称荷载下的全尺寸铝合金板式节点有限元模型见图11a。

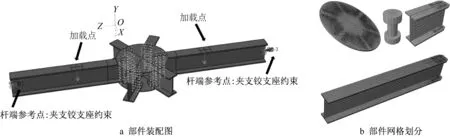
图11 节点有限元模型Fig.11 Infinite element model of joint

所有部件均采用三维线性减缩积分六面体单元（C3D8R）进行模拟。由于螺栓孔附近建立了较多接触关系，故加大了螺栓孔附近单元密度，各部件具体网格划分见图11b。铝合金节点板及杆件经不同过火温度处理后的材料性能由拉伸试验得到。不锈钢螺栓的本构关系采用双折线模型，弹性模量和屈服强度均可取为其常温下的值［23］。边界条件在初始时间步施加。其中，在杆件中部施加强迫位移，以模拟实际加载情况；杆端通过设置参考点施加夹支铰支座约束。在ABAQUS 有限元模型中通过设置接触对考虑铝合金板式节点不同部件受力时的相互作用，共考虑四大类接触对，各接触对的属性见表3。其中，螺帽与节点板间设置了过盈接触以模拟螺栓预紧力。

表3 接触对参数设定Tab.3 Setting of contact pairs

图12 给出了薄板节点和厚板节点的典型破坏模式图。从图12 可以看出，对于薄板节点，受拉节点板出现了大范围的塑性区，塑性区的分布和块状拉剪破坏线一致；而受压节点板出现了较大的屈曲变形，和试验所得破坏模式一致。对于厚板节点，节点整体向一侧发生弯扭失稳，杆件上出现了大范围的塑性区，并产生较大的弯扭变形，加载点附近有凹痕。由图7 和图12 可知，有限元分析所得的破坏模式与试验现象基本一致。

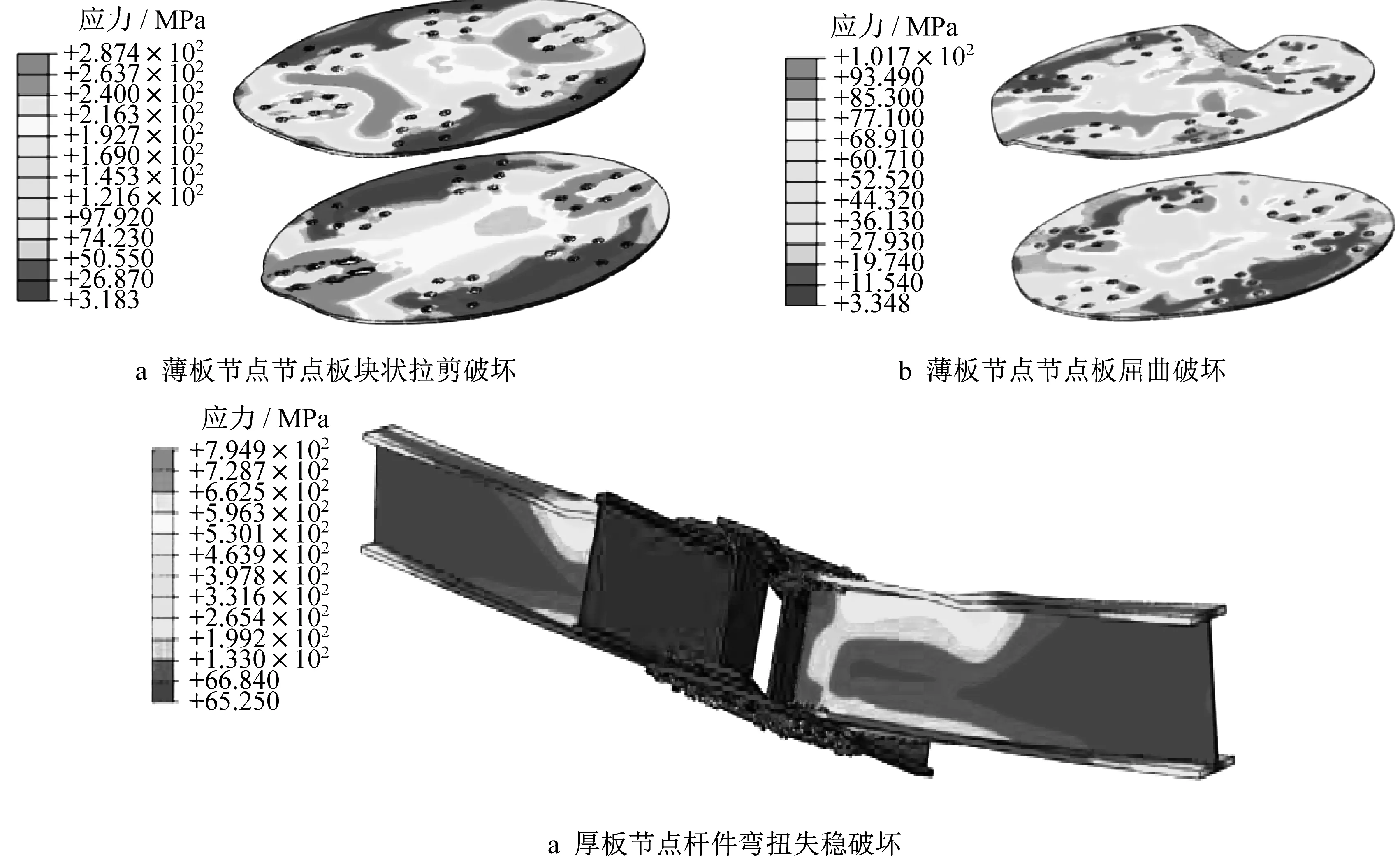
图12 有限元分析结果Fig.12 Numerical results

图13 给出了典型节点J300-2 和J300-5 的弯矩-转角曲线的数值分析结果与试验结果的对比图。从图13可以看出，数值模型计算结果具有较高的准确性。在此基础上，表4 和表5 给出了螺栓嵌固阶段和孔壁承压阶段的刚度和极限弯矩。从表4 可知，在螺栓嵌固阶段，极限弯矩Mf及刚度Kf的试验实测结果与有限元计算结果之间的最大误差分别为1.55%和1.39%，平均误差为0.06%和0.37%；从表5 可知，在孔壁承压阶段，极限弯矩Mc及刚度Kc的试验实测结果与有限元计算结果之间的最大误差分别为6.63%和2.29%，平均误差为1.55%和-0.15%。

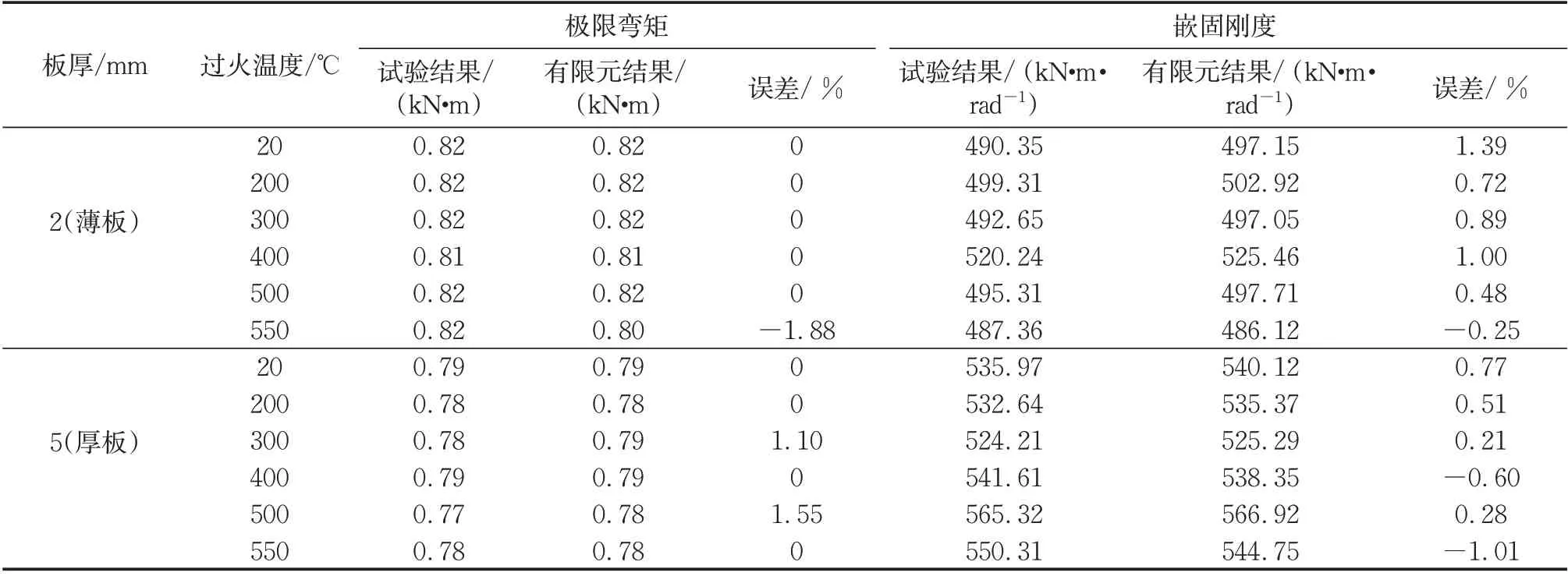
表4 螺栓嵌固阶段试验结果与有限元结果对比Tab.4 Comparison of experiential and numerical results at the stage of bolts fixed

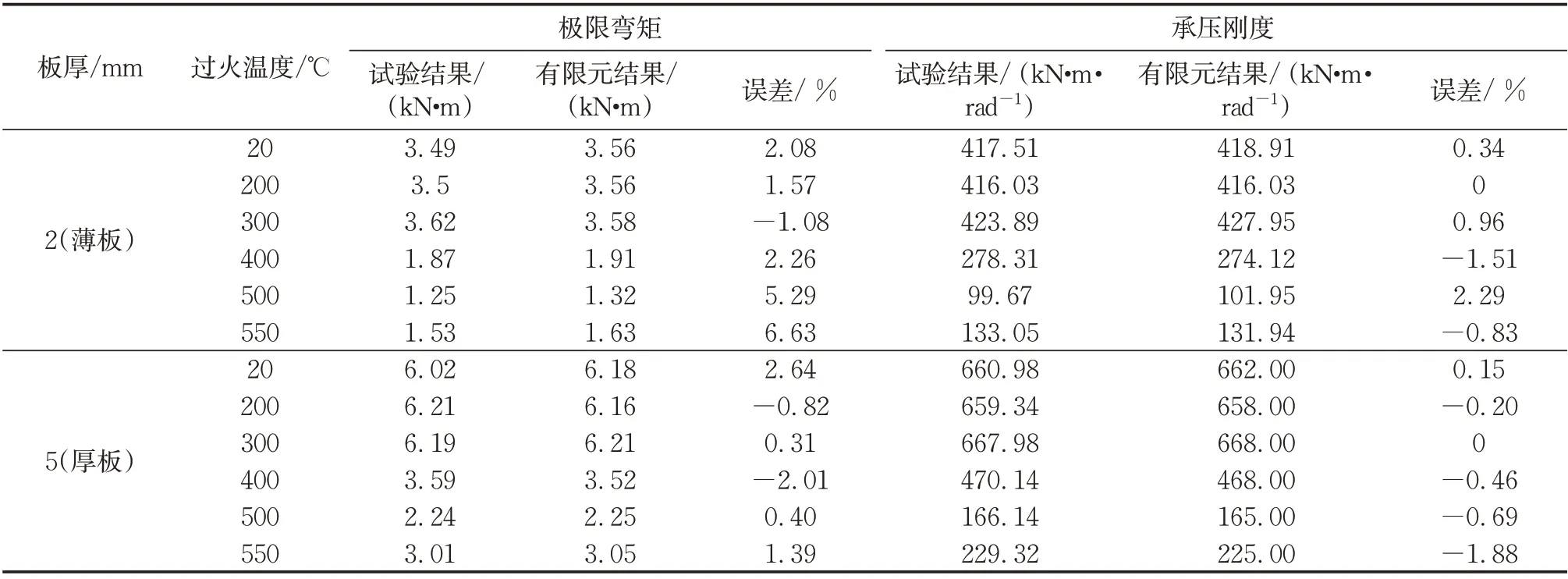
表5 孔壁承压阶段试验结果与有限元结果对比Tab.5 Comparison of experiential and numerical results at the stage of bolt holes pressed

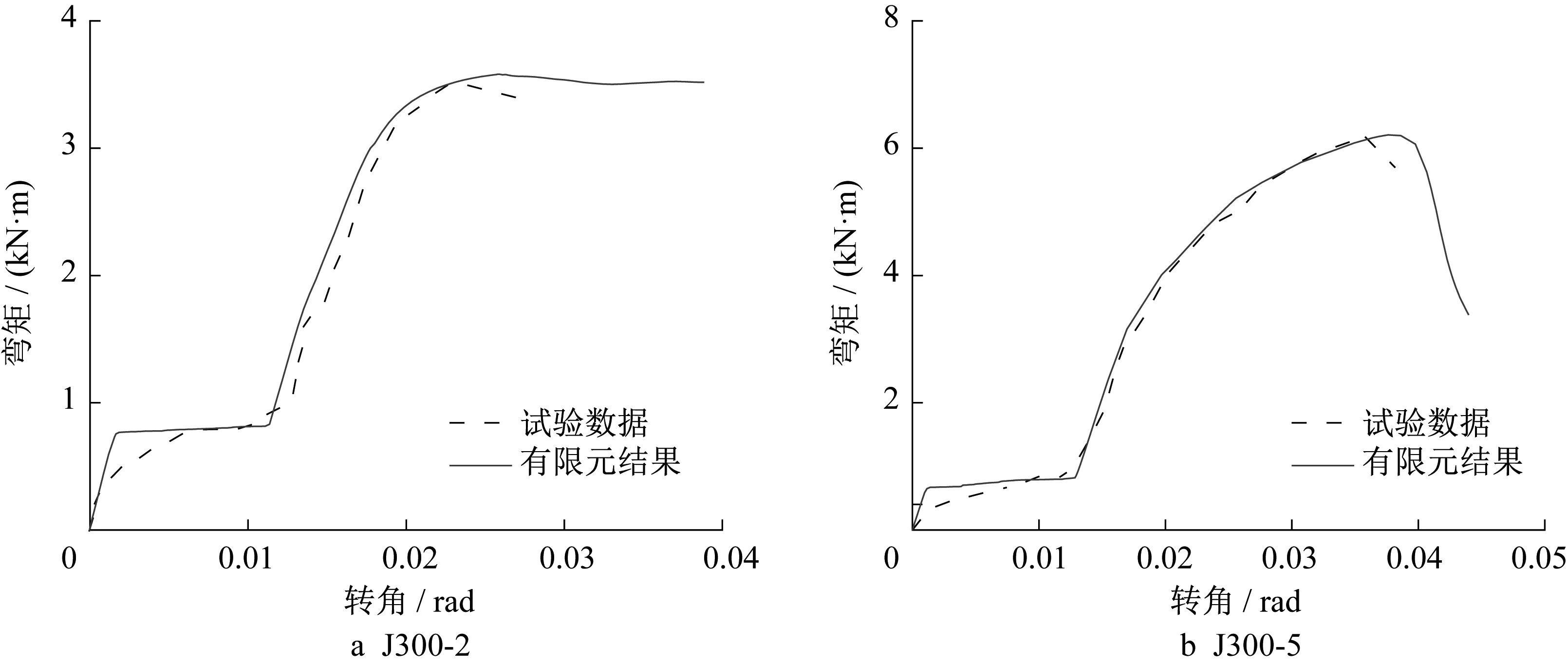
图13 J300-2及J300-5试件的弯矩-转角曲线Fig.13 Bending moment-rotation curves of specimens J300-2 and J300-5

5 参数分析和公式拟合

第4 节研究表明，全尺寸的数值模型和试验结果吻合良好，具有较高的准确性；然而采用全尺寸模型进行大量数值计算效率较低。为此，在全模型的基础上，简化建立了六杆对称荷载下的1/6 尺寸铝合金板式节点有限元模型并进行参数化分析，其建模方法与两杆对称荷载下的全尺寸铝合金板式节点有限元模型完全一致［11］。

共建立20 个1/6 数值模型，如图14 所示。通过改变模型的铝合金牌号、节点板厚度、过火温度等参数以研究材料性能、尺寸规格及过火温度对铝合金板式节点火灾后承载性能的影响规律。节点板厚度考虑2mm 及5 mm 这2 种；铝合金牌号选用6061-T6；过火温度选取常温（20℃）、100℃、200℃、300℃、350℃、400℃、450℃、500℃和550℃。

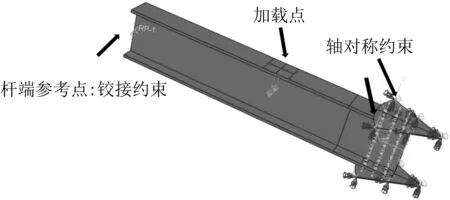
图14 节点的1/6模型Fig.14 1/6 finite element model

汇总所有数值计算结果可知，在不同过火温度条件下，1/6模型的螺栓嵌固刚度KfT、螺栓嵌固极限弯矩MfT随过火温度的变化规律不明显，这与试验结果及全尺寸模型数值分析结果相同。因此螺栓嵌固刚度及螺栓嵌固极限弯矩可采用常温下的计算公式［7］。

在孔壁承压阶段，过火温度对极限弯矩和承压刚度产生明显影响，可以通过设置过火温度影响系数γcT和ζcT来搭建与过火后极限弯矩和承压刚度计算公式与其常温下计算式的关联性。在文献［7］提出的常温下计算公式的基础上，可得火灾后的孔壁承压刚度KcT及承压阶段极限弯矩McT的计算式，如式（3）、式（4）所示：式中：ζcT为孔壁承压刚度过火温度影响系数，考虑了过火后铝合金和不锈钢的热膨胀以及铝合金材料的塑性软化等因素对该阶段刚度的折减程度；γcT为螺栓嵌固极限弯矩过火温度影响系数，考虑了节点过火后对其极限弯矩的折减程度；ET为过火后的弹性模量；fuT为过火后的抗拉强度，其余参数的意义详见文献［7］。

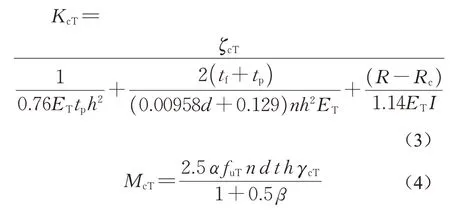
图15 给出了根据1/6 数值模型计算得到的γcT和ζcT随过火温度的变化规律。从图15可以看出，在不同过火温度条件下，孔壁承压刚度KcT及孔壁承压极限弯矩McT与过火温度之间存在明显的“三折线”走势，因此可以采用分段函数的形式进行拟合。孔壁承压刚度过火温度影响系数ζcT及孔壁承压极限弯矩过火温度影响系数γcT拟合结果如式（5）、式（6）所示：

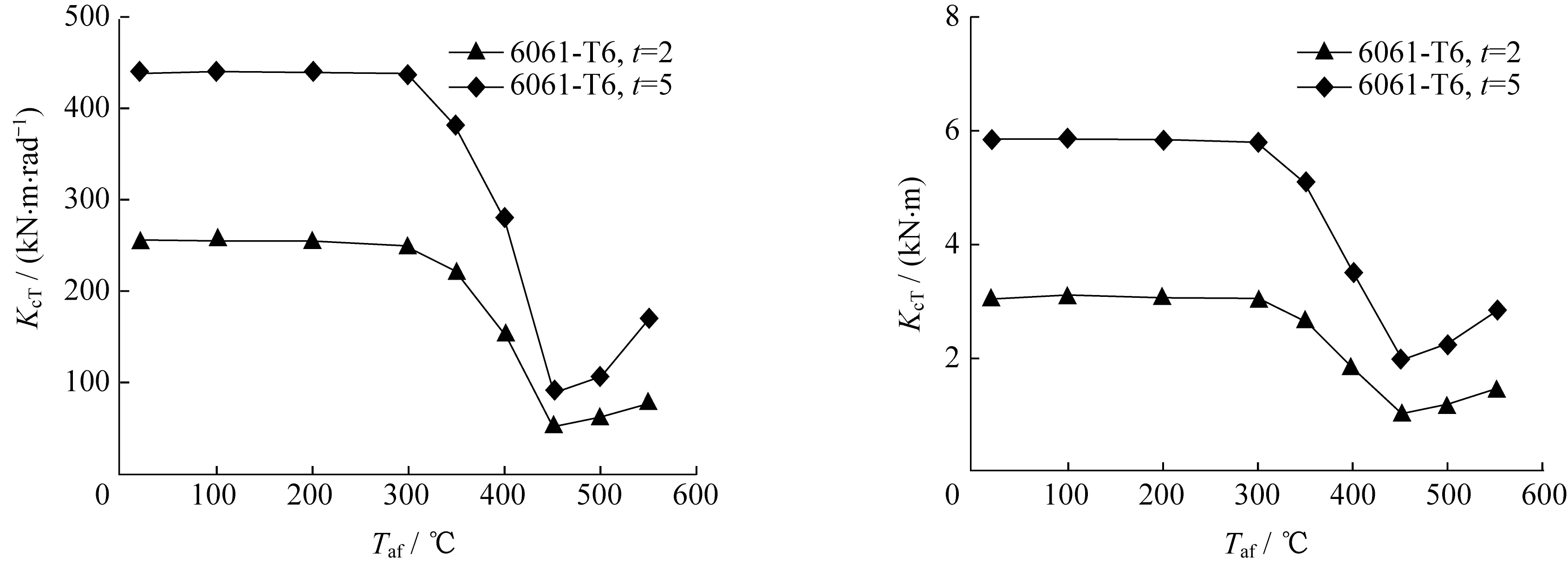
图15 孔壁承压阶段有限元结果Fig.15 Numerical results at the stage of bolt holes pressed

表6 对不同过火温度条件下孔壁承压刚度KcT及孔壁承压极限弯矩McT的误差分析进行了汇总。从表6可以看出，由式（5）、式（6）得到的计算结果和数值分析结果的误差均在5%以内，从而验证了该参数拟合计算式的合理性与准确性。

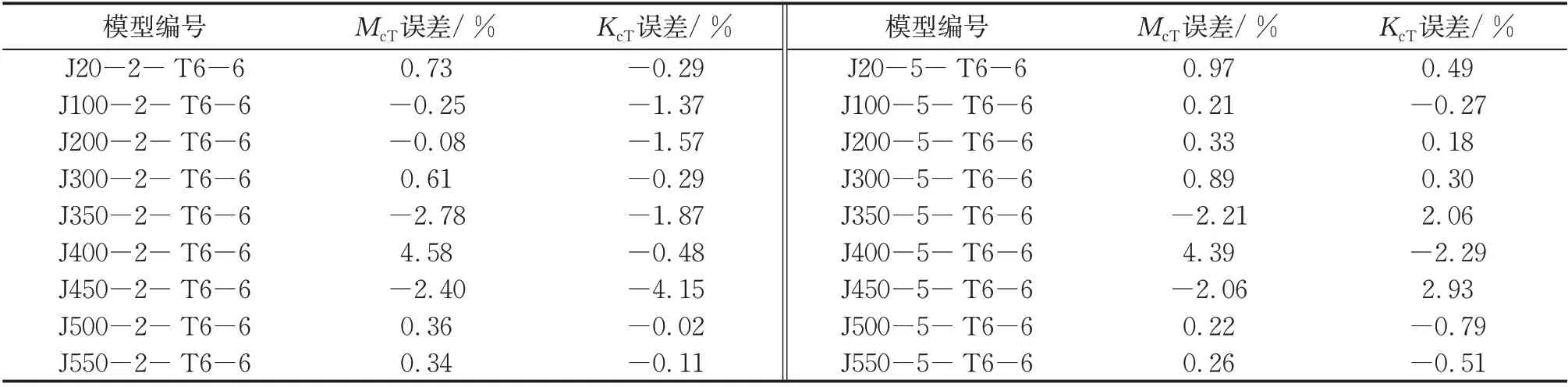
表6 孔壁承压阶段拟合公式与有限元结果对比Tab.6 Comparison of theoretical and numerical results at the stage of bolt holes pressed

图16 给出了过火后弯曲刚度四折线模型与有限元结果的对比情况，图中给出了3 个典型过火温度下的对比曲线。从图16 可以看出，在全过程中，有限元结果与过火后四折线模型基本吻合，式（3）—（6）计算得到的承载力与刚度能较好地反映实际结果。

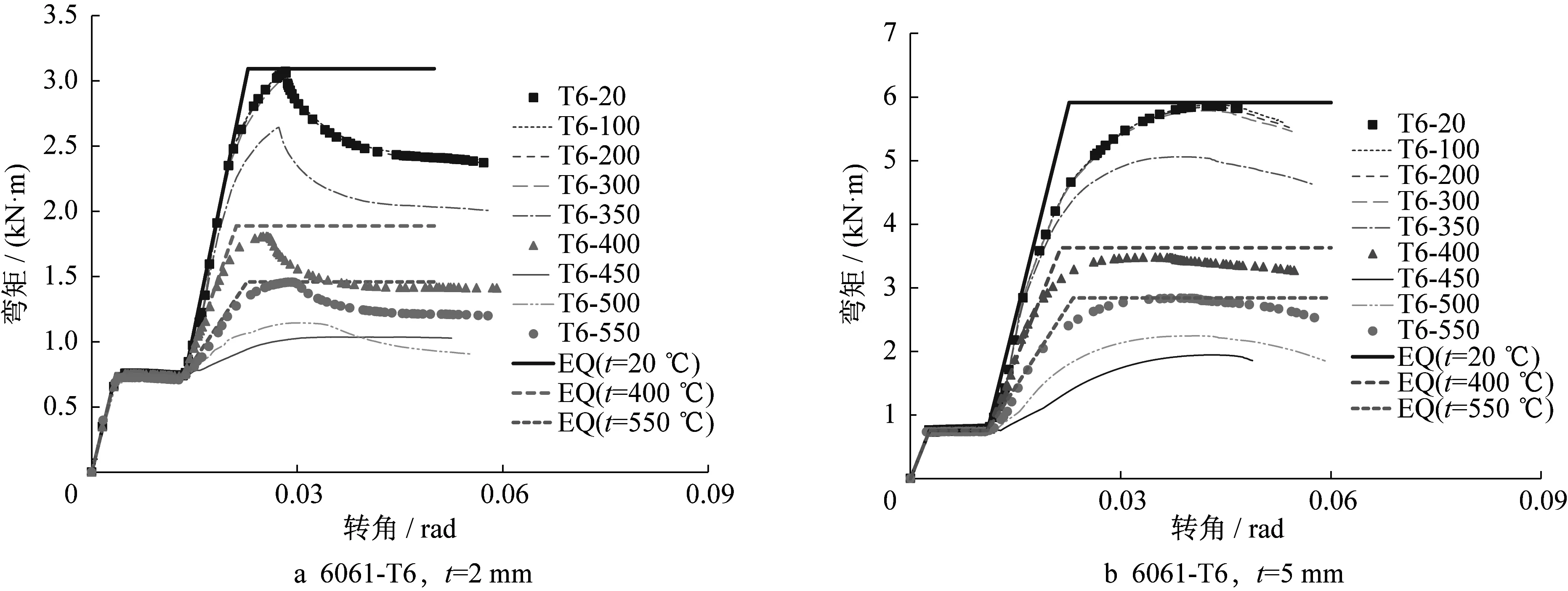
图16 四折线模型及弯矩-转角曲线对比Fig.16 Four-line model and bending moment-rotation curves

6 结论

（1）国产6061-T6 铝合金单次受火经自然冷却后的弹性模量在过火后无明显变化，但材料强度受过火温度影响较大，呈现明显的“三折线”走势；当过火温度高于300℃后，屈服强度及抗拉强度开始迅速降低，并在450℃时达到最低值，降幅达80%和60%，之后随着过火温度的继续升高，其屈服强度及抗拉强度会出现小幅度的恢复。

（2）铝合金板式节点在过火后发生的破坏模式与常温下的破坏模式基本相同；其中，薄板节点试件发生受拉节点板块状拉剪或受压节点板屈曲破坏，厚板节点试件发生杆件弯扭失稳破坏。

（3）铝合金板式节点过火后弯矩-转角曲线中的螺栓嵌固阶段极限弯矩Mf及刚度Kf基本没有折减，与过火温度无明显关系，与常温下一致。

（4）铝合金板式节点过火后弯矩-转角曲线中的孔壁承压阶段极限弯矩Mc及刚度Kc与过火温度有明显关系，呈现“三折线”走势。

（5）火灾后铝合金板式节点的弯矩-转角曲线也可采用常温下的四折线模型描述，在常温条件下各阶段的弯曲刚度计算式的基础上引入过火温度影响系数，可考虑过火温度对预紧力及材料热膨胀等因素对各阶段极限弯矩及刚度的影响。

作者贡献声明：

郭小农：指导论文开展、文章撰写与修改工作。

徐泽宇：参与理论分析、试验研究及文章初稿撰写。陈 晨：参与试验研究。

罗金辉：指导理论分析及文章修改工作。