基于超构材料设计吸声降噪结构的研究进展
潘永东,宋 潮,赵金峰,张晓青
(1. 同济大学航空航天与力学学院,上海 200092;2. 同济大学物理科学与工程学院,上海 200092;3. 同济大学上海特殊人工微结构材料及技术重点实验室,上海 200092)
随着工业和城镇化的不断发展[1-2],噪声的影响越来越突出,已经成为了显著的环境问题之一。在日常生活方面,噪声不仅会损伤听力,而且会诱发睡眠障碍和多种生理疾病[3];在社会发展方面,工厂作业产生的噪声严重影响其运营状态和效率[4];在国防领域,噪声的辐射增加空中侦察机和水下潜艇等设备被敌军探测的风险,并且对其自声呐系统产生不利影响,显著降低其隐蔽能力和安全性能[5-7]。故噪声不仅对人体健康产生极大负面影响[8-11],而且阻碍国民经济发展、危害国防安全[12-14]。
噪声是声波的随机变化,声压、频率以及声源都是随时间瞬态变化的[15],且可听声范围内的声波在介质中的耗散非常微弱[16-18],如低频声波的波长可达到数米,其衍射效应明显。图1 统计了近年来在Web of Science 中发表的吸声论文的数量。从2010年起,关于吸声结构的论文数量呈逐年增加的趋势,表明吸声结构逐渐成为学术研究的热点,这也体现了当代社会对吸声结构的迫切需求。
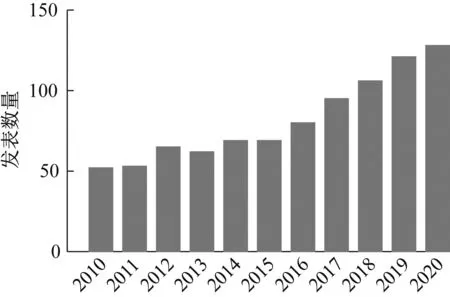
图1 发表论文的数量与出版年的关系Fig.1 Histogram of publication year and number of papers published
传统多孔材料的吸声基于其微孔结构,通过将声能转换为热能实现吸声。根据文献[19],多孔材料的厚度近似等于声波波长的1/4才能实现对应频率的吸声,因此在高频范围内有较好的吸声效果[20-21],而对低于500 Hz 的低频声波则需要较大的厚度(至少17 cm)才能实现。共振型吸声材料主要有薄板共振结构、微缝共振结构、穿孔板共振结构、微穿孔板共振结构等。其中,微穿孔板共振结构的厚度可缩小到共振波长的1/9[22],具有优异的中高频吸声性能。
声学超构材料是一种由单元组成的人工周期性结构[23-34],因其新颖的声学响应性质而受到广泛关注。声学超表面则是超构材料中的重要分支,是指由亚波长微结构单元(λ10 ~λ,λ为声波波长)组成的二维表面结构。超构材料的局域共振特性增加低频状态下的体密度[35-36],进而有效降低了结构的共振频率,实现小尺寸结构单元调控大尺度声波。目前,基于超构材料的吸声结构可实现深亚波长的极低频近完美吸声[29],因此,超构材料在低频吸声领域具有强大的应用潜力。其中,很多学者致力于研究可调控的吸声结构[23-24,37],如有学者将压电材料与声学结构结合起来,通过外部电路控制电压信号,由逆压电效应调控吸声性能[38-39]。然而,低频范围的宽带吸声依然是有待解决的重要前沿问题。
本文首先回顾了吸声的主要机制,包括声学黏滞性理论和热传导理论;简要介绍吸声结构的研究方法,主要有阻抗分析方法、仿真计算分析方法以及实验分析方法。在此基础上,根据目前已发表的文献对吸声结构进行分类和介绍,深入介绍基于超构材料设计的研究进展,并讨论其未来可能的发展方向。
1 声学吸收机制与研究方法
1.1 声学吸收机制
由于实际媒质中存在黏滞作用,声波在其中传播时,会被吸收一部分声能,黏滞力的存在使得同一界面上相邻质点的运动速度存在差异,并且带动周围媒质质点运动,引起媒质的压缩和膨胀现象,形成温度梯度,进而产生热传导[40]。这2 种机制都是频率依赖的,其对声波的耗散能力近似正比于频率的平方,因而对高频声波的吸收性能更为显著[36,41-42]。
1.1.1 声学黏滞性理论


图2 声波在管中传播的仿真结果Fig.2 Simulation results of sound propagation in straight tube
当声波在一个半径为a、长度为l的圆柱形管中沿着轴向(x轴)传播时,考虑管壁的黏滞作用时,运动方程为[40]

式中:u为声速;p为声压;ua、pa分别是半径为a处的声速和声压;K为流体导热率,K=(1-j)δv;J0为零阶柱贝塞尔函数。由式(2)可知,在同一截面,ua的大小与径向位置r密切相关。
1.1.2 热传导理论

1.2 研究方法
目前关于吸声结构的主要理论研究方法包括阻抗匹配法、复频率平面法、耦合模式理论(Coupled mode theory,CMT)和因子提取法。
耦合模式理论是从量子动力学中引申出来的概念,文献[43]中有详细介绍。

在阻抗匹配分析法中,阻抗匹配即结构的声阻抗与空气特性阻抗相等,使入射声波完全进入结构中而不产生反射波,可用于揭示声学结构的声学性能[18,29,45-52]。吸声结构的反射系数r与吸声结构表面声阻抗率Zs之间的关系可用式(3)表示:

其中,Z0=ρ0c0为空气的特性阻抗。对于反射型的吸声结构,其吸声系数α可表示为α=1-|r|2,将该式进行归一化处理,得到

式中:ξ=ZsZ0=xs+jys为归一化表面声阻抗率;xs和ys分别为声阻率比和声抗率比。
复频率平面分析方法是一种有效的设计宽带吸声结构的经典方法[53-55],可用于研究系统的物理特性。通过在波数上引入虚部,也就是将k′=ke+jki代替波数k,ke为系统的固有波数,ki为引入的虚波数,通过复频率平面内实频率f和虚频率fi的分布可以分析吸声结构的反射特性和吸声特性。将k′代入到吸声结构的声阻抗中,记为Z′s,得到反射系数r′=(Z′s-Z0) (Z′s+Z0)表示成关于实频率和虚频率的函数,其中Z0为空气的声阻抗。在复频率平面内,绘制关于lg|r′|的云图,r′为反射系数。通过分析云图上零极点的位置可判断系统是否处于完美吸声,具体分析方法如图3。

图3 完美吸声体的复频率平面分析示意Fig.3 Diagram of complex frequency plane illustration for perfect absorber (r′being the reflection coefficients)
在无损耗系统中,反射系数的零点和极点位于实频率轴,对称地分布在复频率平面上,其对应的实频率为系统的共振频率;当系统考虑损耗时,反射系数的零点和极点将沿着虚频率轴的正方向移动。当固有损耗与辐射损耗相等时,零点处于实频率轴上,如图3中圆圈所示,则系统满足临界耦合条件,实现完美吸声,故以此可判断系统是否实现完美吸声。
1.3 仿真计算分析方法
近些年大部分研究学者使用有限元软件COMSOL Multiphysics中的压力声学模块仿真分析吸声结构。在使用压力声学模块时,使用平面波辐射设置入射声压场,如果是透射型吸声结构,则需要设置出射界面为平面波辐射,避免声波遇到硬边界形成二次反射波,影响吸声系数的计算。当所设计的吸声结构的声阻抗远大于空气的特性阻抗时,可将结构边界设置为硬边界,这样将简化计算过程,避免多物理场耦合,很大程度上减少计算时间;当所设计的结构包括管状、腔体、孔洞等结构时,需要考虑热损耗和黏滞效应,这些精细部分的仿真需要用到狭窄区域声学进行计算。
1.4 实验分析方法
吸声系数的测量体系主要有混响室法、阻抗管法和自由场法[56]。主要介绍基于阻抗管的吸声系数测量方法。阻抗管是测量吸声系数的专用设备,主要供应商包括丹麦的Brüel&Kjær公司和北京声望声电技术有限公司。商用阻抗管的尺寸是固定的,且大多数为圆柱形结构,限制了其他截面形状的吸声结构的测试,在已发表的论文中也出现截面为正方形的自制阻抗管[57-59]。主要的测试过程是:计算机控制驻波管中的扬声器发出平面波,安装在驻波管上的标准麦克风采集声压信号并通过数据采集卡传送回计算机,通过计算机上的配套软件进行处理,基于传递矩阵法或三传感器法、四传感器法计算得到测试结构的吸声系数。3D 打印技术具备打印精密器件的能力,是现阶段精密吸声结构制备的主要选择方向。目前的3D打印可以实现0.5mm的打印精度,且可选择的材料包含金属、树脂、尼龙、软胶等,以满足不同的应用需求。
2 吸声结构
目前的吸声结构可以分为传统吸声结构和基于超构材料的吸声结构。传统的吸声材料按吸声机理的不同,可分为多孔吸声材料和共振吸声结构。多孔介质的吸声特性可以通过有效介质理论解释[18]。共振型吸声结构通过共振增加声能密度,提高声波的黏滞和耗散能力,使吸声性能更强。基于超构材料设计的吸声结构按照共振类型可以分为薄膜复合共振型超表面、卷曲空间型超表面和亥姆霍兹谐振腔型超表面。
2.1 传统吸声材料与结构设计
传统材料用于吸收低频声波时,其厚度近似为声波波长的1/4[19,34],即吸声性能与结构厚度密切相关。因此,在空间受限的情况下,多孔材料的实际应用将受到影响。为有效降低多孔材料在低频吸声时的结构厚度,目前常见的方法是将其填充到含有腔体的吸声结构内部[60]或与其他声学器件耦合[48],基于多种耗散机制耦合实现吸声,或覆盖在吸声结构表面用于提高系统损耗。
2019 年Yoon 等[21]提 出 了 使 用 拓 扑 优 化 算法在多孔结构中夹杂刚性板,激发多种共振机制,1 500 Hz 情况下的吸声系数几乎为1,结构厚度为2cm。2020年Xie等[60]在同等结构厚度的情况下,将聚酯纤维填充到蜂窝结构中形成一种混合结构,如图4a所示,在3 000 ~6 000 Hz内,结构的平均吸声系数大于0.8。

图4 参考文献中涉及的声学吸声结构图Fig.4 Diagrams of acoustic and sound absorption structures in references
为了获得更好的低频吸声性能,Zhao 等[48]提出将三聚氰胺泡沫和迷宫通道结合,将2 种不同的损耗机制结合以提高低频吸声性能,在491 Hz 处实现完美吸声,结构厚度与工作波长的比值为1/25。
在共振吸声结构中,应用最广泛的是微穿孔板吸声结构,因其在较宽的频率范围内能实现高的吸声性能。马大猷先生很早提出了微穿孔板的等效电路理论[61],详细分析了微穿孔吸声器的基本声学特性,指出其缺点是在低频范围的吸声性能较差[62]。
为提高微穿孔板吸声器的低频吸声性能,很多研究学者在孔形设计方面做了相关研究。2018 年Zieliński 等[63]设计了一种特殊的微缝孔共振吸声结构,该孔型的吸声结构在750 Hz处的吸声系数为1,比方形微穿孔板的吸声系数提高了0.2。2020 年Carbajo 等[52]提出具有斜穿孔的微穿孔板结构,该结构的斜射角度从0°增至60°时,共振频率由1 730 Hz移动到1 000 Hz,吸声系数由0.07提高到0.89。
在结构耦合方面,2016 年Li 等[50]将穿孔板与内插管相结合显著提高了结构的低频宽带吸声性能,如图4b 所示。所设计的结构在125 ~250 Hz 处的吸声系数大于0.8,结构厚度为10 cm。
在多层微穿孔板结构的设计方面,2017 年Qian等[51]通过串并联方式设计了一种背腔分隔的复合微穿孔板吸声器,如图4c所示。结构厚度为5.85 cm,在500 ~2 000 Hz的平均吸声系数大于0.85。
为实现可调吸声性能,2015年Duan等[38]使用铁电聚偏氟乙烯薄膜(PVDF)作为微穿孔板的原材料,如图4d,通过逆压电效应尝试实现可调吸声,在500 Hz 处的吸声系数约为0.4。随后,Kong 等[37]将PVDF 薄膜的穿孔率增大,通过改变激发频率实现可调吸声,在550 Hz处的吸声系数可达到0.8。
综上,传统吸声材料通常需要与声学结构结合设计,在中高频范围的吸声性能较好,而在低频范围的吸声性能较低,且加工困难,因此很难实现深亚波长尺度(<λ10或<λ20)的低频高效吸声。
2.2 基于超构材料设计的吸声结构
2.2.1 薄膜、薄板复合型超构材料
文献[28,64]最早将薄膜材料应用于吸声材料,提出了镶嵌薄膜共振结构(decorated membrane resonator,DMR)。该结构主要由弹性薄膜和附着在其上的刚性质量片构成,弹性薄膜需张紧,用于提供回复力,如图5a 中的样品B,每块弹性薄膜的长、宽、厚分别为159 mm、15 mm、0.2 mm。每块薄膜的表面镶嵌有8 片半圆形的金属片,共有左右2 组,每组有4片,对称分布在左右两侧,相距32 mm。在共振频率处,质量片的拍打模式极大增加了局域声能密度,扩宽了结构的吸声频带(100 ~1 000 Hz),如图5b中曲线所示,测试装置为2层样品B,样品之间的间隔为28 mm,并在后方28 mm处放置一块铝板。吸 声 峰 值 分 别 位 于164、376、511、645、827 和960 Hz。箭头为有限元得到的吸收峰频率位置,实验与仿真结果一致,最低吸声频率为164 Hz,而整体结构厚度只有56 mm,为对应波长的1/37。
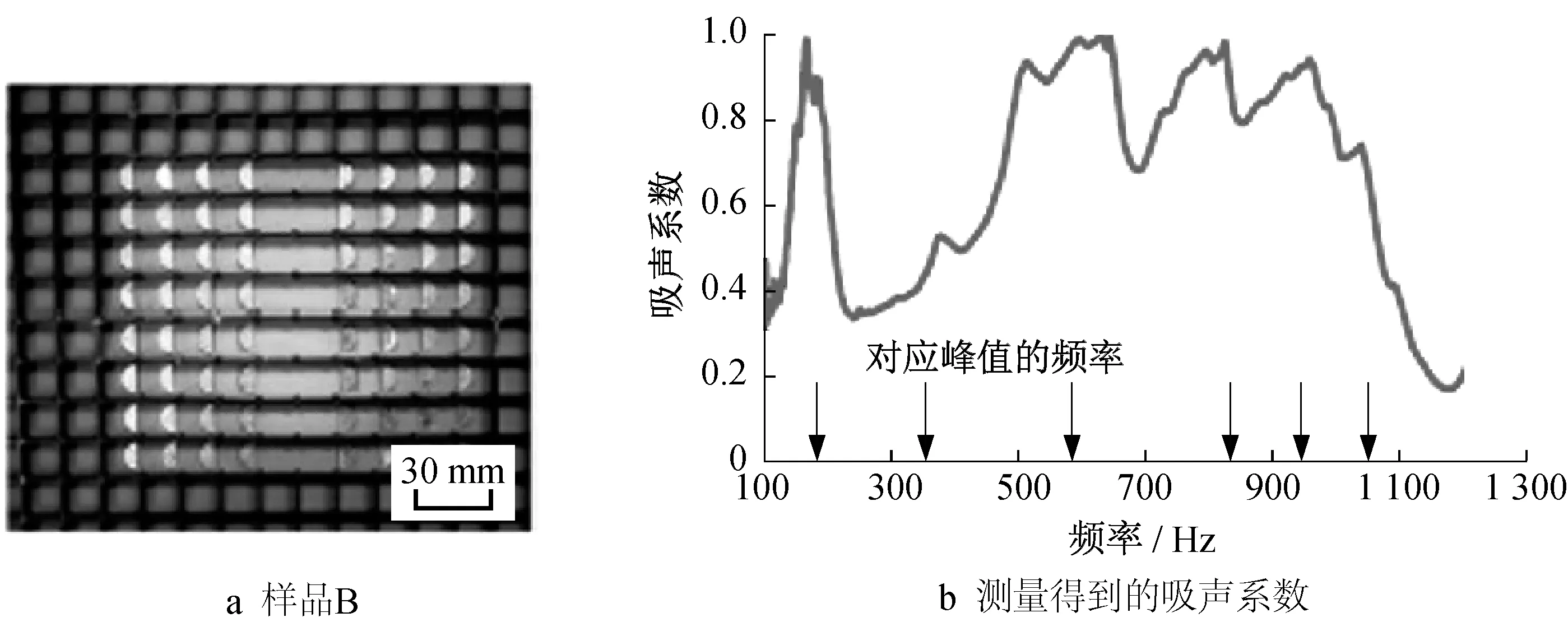
图5 样品B及其实验结果[28]Fig.5 Sample B and absorption results of experiment[28]
随后,Ma等[26]在此基础上设计了一种基于杂化共振的薄膜吸声器(Hybrid Membrane Resonator,HMR),该结构是在镶嵌有质量片的薄膜共振器的基础上增加空气腔体和背衬结构,如图6所示,图中a1为薄膜半径,s为密封腔体的深度,k为入射声波的波矢,W为薄膜的实际位移,Ws为入射声波振幅。由于薄膜与背衬间的多重反射,形成新的杂化共振模式,在共振频率152 Hz 实现了单端口入射声波的全吸收。并且在系统中引入磁场,在入射声波的作用下,粘贴在薄膜上的导线切割磁力线而产生电流,声电转换效率为23%,同时实现了单频吸声和声能采集。Yang等[65]针对该结构进行了理论分析,研究了声波在单向入射和双向入射情况下可实现的吸收能量极值问题。随后,Yang等[66]设计了一种基于简并共振的镶嵌薄膜吸声器,当单极子共振与偶极子共振的频率相同时,就会发生简并,此时会完全消除散射,实现完美吸声。Li 等[67]将压电效应引入薄膜共振的超构材料中,同时实现了隔声与声能采集,并研究了薄膜张力对吸声效果的影响。

图6 超表面单元结构的几何示意图和共振特性[26]Fig.6 Geometry diagram and resonance characteristics of unit cell of metasurface[26]
2019年Liao等[39]基于2种压电材料设计了可调的吸声超构材料,建立了压电-结构-声耦合模型用于分析吸声性能。其自适应机制可根据入射波频率调节超构材料的声阻抗以满足阻抗匹配。在112 ~236 Hz 的平均吸声大于0.9,而超构材料厚度仅为30 mm。
为避免薄膜张力对吸声性能的影响,Li 等[68]使用薄板进行吸声。在薄板中心位置以及薄板上下两侧分别放置磁铁,由此在薄板两侧产生强吸引力,通过磁场与板之间的相互作用在127 Hz处实现高效吸声,增大磁场强度将使吸声峰值频率向低频移动并且增加吸声带宽。
综上,薄膜复合型超表面主要是由张紧的弹性薄膜和贴附在其上的刚性质量片组成。薄膜厚度一般为数百微米,可在深亚波长尺度下实现吸声,然而,薄膜张力影响结构的吸声效果,增加样品制备的难度,使系统的稳定性受到影响;且薄膜类结构具有高品质因子,限制了其在吸声降噪领域中的应用。薄板复合结构虽然避免了张力对实验结果的影响,但是需要较强的外力才能使薄板运动,适用场景受到一定限制。
2.2.2 卷曲空间型超构表面
卷曲空间型超构表面主要是通过折叠空间的方法压缩共振腔以增加声波传播的路径,从而调控声波相位实现吸声。2014年Cai 等[46]基于亥姆霍兹谐振腔设计了共面螺旋管超表面,通过将谐振腔的腔体卷绕增大腔体长度,实现低频吸声。在理论和实验上实现了在250 Hz 处的高效吸声,对应波长为结构厚度的100 倍。2016 年Li 和Assouar[47]将微穿孔板与卷曲型折叠超表面结合,如图7 所示,图中d为穿孔直径,a2为穿孔常数,l2为腔体深度,t为微穿孔板厚度,a3为超表面边长,d1为穿孔直径,b为实心梁厚度,w为空腔厚度。使用理论和仿真分析方法研究了该结构的吸声特性,实现极低频(125.8Hz)下的完美吸声,结构厚度仅为波长的1/233。

图7 传统微穿孔板系统与超表面结构[47]Fig.7 Conventional perforated system and metasurface structure[47]
为了扩宽吸声带宽,2016 年Zhang 和Hu[49]将6个完美吸声的卷曲空间结构拼装成声学超表面,如图8 所示,图中h为结构厚度,a为横截面边长,t1为隔板厚度,h1、h2、h3为高度,p1为通道宽度,Ⅰ-Ⅲ为层标号,1-6分别表示6个卷曲通道。该结构实现了105 ~171 Hz 内的宽带吸声,吸声系数大于0.9,结构厚度仅为波长的0.07 倍。文中通过耦合模式理论计算了系统的声阻抗,由阻抗匹配计算得到共振频率与腔体长度之间的关系,进而确定在各共振频率下的腔体长度,并将各部分腔体有机地组合起来。
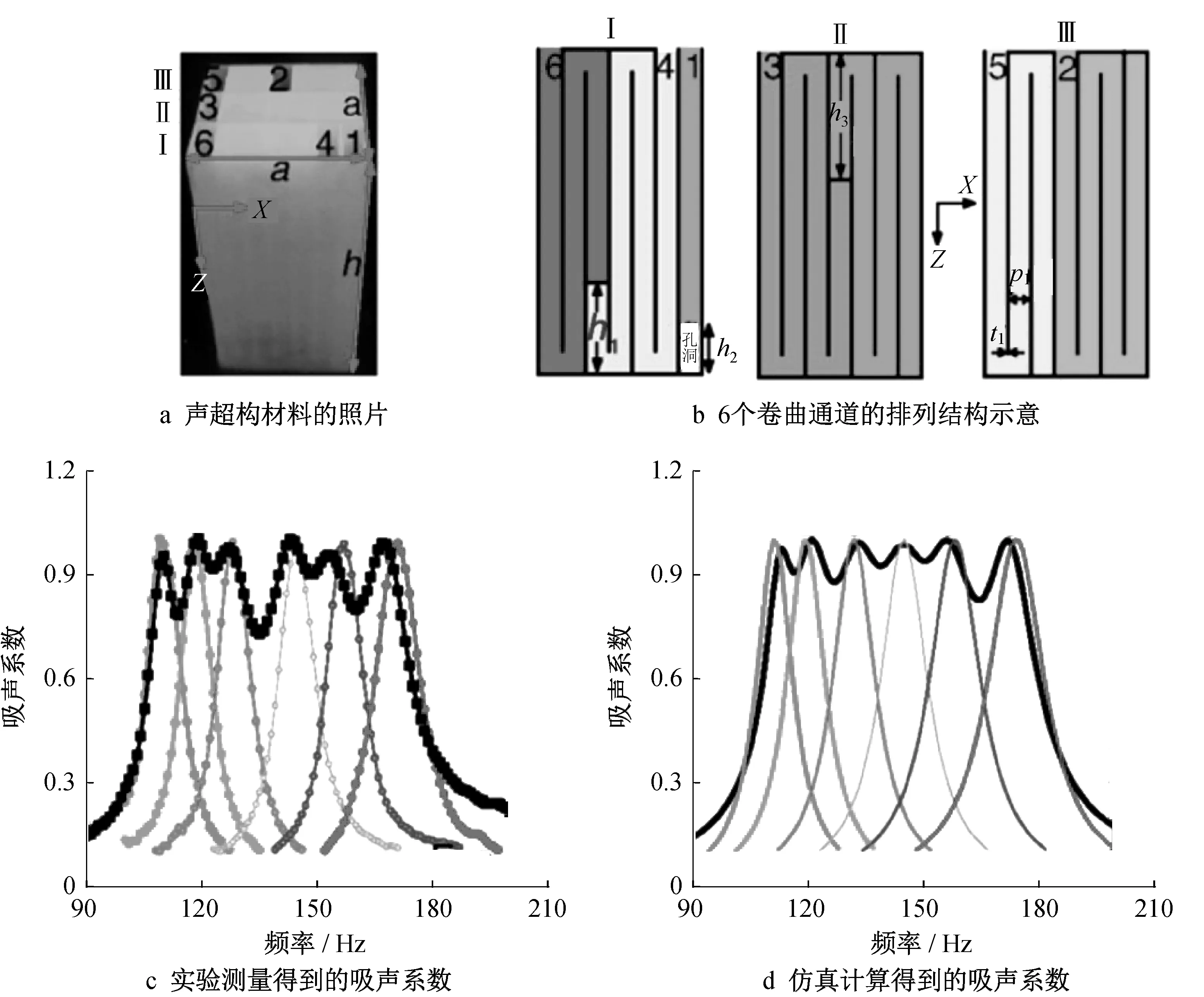
图8 一种三维单端口卷曲型超构材料[49]Fig.8 Experimental realization of a 3D single-port LAMM with broadband absorption[49]
为进一步降低结构厚度,2018 年Huang 等[69]设计了共面卷曲结构的吸声超表面,引入插入管结构调控系统的声阻抗进而实现可调的完美吸声。文献[70]应用Crandall 理论得到插入管的声阻抗,再结合卷曲腔体的声阻抗得到系统的总阻抗,研究了插入管的半径和管长对结构声阻与声抗比值的影响,对插入管结构优化具有指导作用。
为实现声电转换,2019年Jin等[71]将压电片与卷曲空间型超表面结合,压电片放置于在共振频率处声压最大的位置,将穿孔板理论和阻抗转移理论结合,分析了系统的吸声性能,与仿真结果具有一致性。在共振频率处,声波被局限在超表面内,声能密度被急剧放大,在1 303 Hz 处实现声能吸收和能量采集,结构厚度为声波波长的1/63。
为了在结构厚度不增加的情况下降低结构共振频率,Donda 等[29]将卷曲通道放置于含有内插孔的卷曲空间中,提出了多卷曲超表面的概念(multicoiled metasurface,MCM),既充分利用了卷曲腔的空间,同时增加了额外的自由度,以此削弱腔体长度对卷曲空间共振频率的影响,使用声电等效电路对系统进行分析,实现了在深亚波长尺度(<λ20)上的极低频(50 Hz)吸声,结构厚度(13 mm)仅为波长的1/527。该结构的物理机制是基于螺旋卷曲腔、迷宫通道和由卷曲形成的类亥姆霍兹腔体的复合共振机制,声波在结构中的传播路径不仅包括卷曲通道,还包括嵌入在其内部的迷宫通道,相对于传统的1/4波长谐振腔,增加了波长的传播路径,故使共振频率向低频移动。在此基础上,作者设计了超晶胞结构实现了极低频宽带吸声(49 ~53 Hz)。
2019 年Long 等[32]在具有全反射的刚性壁中周期性地嵌入了卷曲空间谐振腔(coiled space resonators,CSRs),实现单端口亚波长完美吸声,如图9所示(图中PI为入射声波,PR为反射声波,D为2个吸声器之间的距离,H为高度,T为海绵层厚度,Dy、Dz分别为结构在y、z方向上的周期常数),使用耦合模式理论对系统进行分析,并使用复频率平面方法证明了临界耦合。为扩宽吸声频带,将6 个不同共振频率的单元结构耦合,并在表面覆盖薄层海绵增加系统损耗,实现了228 ~319 Hz 的宽频近似完美吸声,对应波长为结构厚度的12.6 ~9.0倍,吸声系数大于0.95。此外,该课题组将单个单元的吸声器以低填充率的方式嵌入刚性墙中[72],将全反射的刚性墙转换为完美吸声体,实现了185 ~385 Hz 的宽频吸声,吸声系数大于0.8,而对应波长为结构厚度的17.7 ~8.5倍。

图9 低填充率吸声结构示意与多频带吸声系统示意[32]Fig.9 Schematic of ultrasparse absorptive system configuration at a low filling ratio[32]
由传输线阻抗转移理论可知,卷曲空间型超构表面需要1/4 波长的结构空间才能实现阻抗匹配,因此在低频处时,结构尺度会较大,故需结合多种共振模式降低结构尺度;而一旦内部结构固定,其吸声频率也随之被确定,使该类型的吸声结构在调节吸声带宽方面面临挑战。值得关注的是Sun等[73]提出了一种号筒状中空的螺旋型超表面用于隔声,同时实现了多入射角下的宽带隔声和高效通风,并进一步结合耗散和干涉机理,设计了多角度入射下的超宽带通风隔声装置[74],工作频率范围为650 ~2 000 Hz,显著提高了其在工业领域的应用。因此,在吸声的同时保证空气的流通将是吸声结构的发展方向之一,这将有利于吸声结构在日常生活中的应用。
2.2.3 亥姆霍兹谐振腔型超表面
亥姆霍兹谐振腔(Helmholtz resonators,HRs)相比于法布里珀罗(Fabry-Pérot,FP)谐振腔具有更小的颈口,可提供较大的声阻,通过较小的体积实现低频吸声,因此,很多研究学者应用亥姆霍兹谐振腔实现低频完美吸声。
2016 年Jiménez 等[35]基于亥姆霍兹谐振腔设计了深亚波长尺度的超薄声超材料。通过控制亥姆霍兹谐振腔和狭缝的尺寸,调节系统的热粘损耗,使系统满足临界耦合条件。2017 年Jiménez 等[75]又提出了腔体高度梯度变化的亥姆霍兹谐振腔阵列,如图10所示,图中d3为结构高度,h[n]1为波导宽度,L为结构厚度,n为亥姆霍兹谐振腔编号,N=9,a[n]为波导长度,h[n]3为波导高度。该结构实现了300 ~1 000 Hz的宽频完美吸声,结构厚度为11cm。
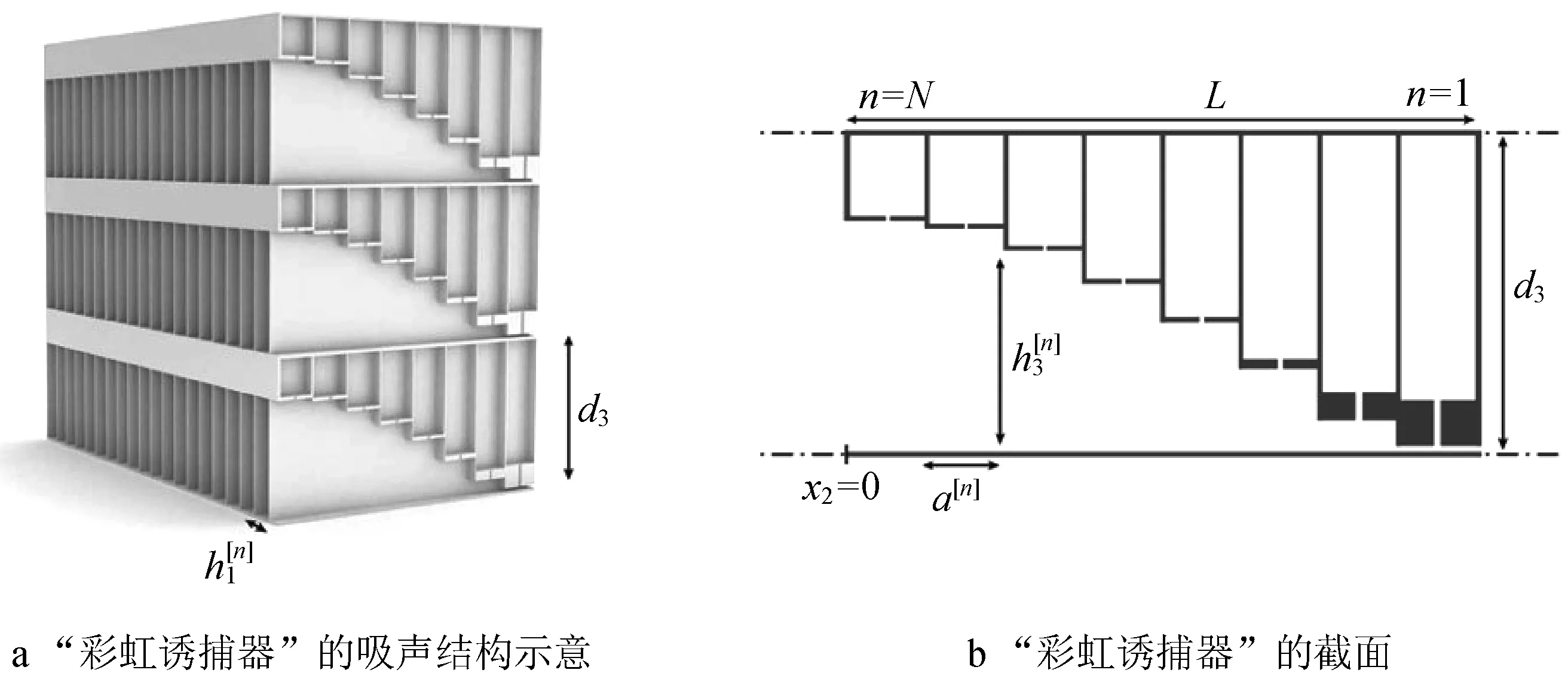
图10 “彩虹诱捕器”的吸声结构示意与截面示意[75]Fig.10 Conceptual view of a rainbow trapping absorber and its section diagram[75]
为降低结构厚度,2019 年Huang 等[45]将内插管与亥姆霍兹谐振腔结合,通过调节内插管的直径和管长实现了不同频率的完美吸声,如图11 所示,图中da为内插管直径,la为内插管长度。理论分析了内插管壁的热粘损耗和端部补偿,与实验和仿真结果一致,如图11c中实线和点线所示,而结构厚度仅为波长的1/50。2020 年Huang 等[55]将多个嵌入内插管的亥姆霍兹谐振腔组合形成超表面,设计了低频宽带的吸声结构(298 ~479 Hz,870 ~3 224 Hz),结构厚度分别为5.0cm、3.9 cm,平均吸声系数高于0.95,体现了内插管在调节系统阻抗并实现可调带宽的极大优势。

图11 样品图与吸声系数结果[45]Fig.11 Photograph of experimental sample and sound absorption results[45]
分析参考文献中的吸声频率与吸声系数的研究,如图12a 所示,图中深灰色、中灰色和淡灰色分别代表低频(<500 Hz)、中频(500 ~1 000Hz)和高频(>1 000 Hz)区域,可以看出吸声频带已基本覆盖中高频区域,而对100 Hz 以内的吸声研究还较少。其次,分析了参考文献中的吸声频率与发表年份的关系,如图12b所示。由图可知,低频吸声是近年研究的热点,同样在100 Hz 以内对极低频吸声的研究较少。最后,统计参考文献中的工作波长λ与结构厚度D之间的最大比值,在不同吸声结构设计中的分布如图12c。可以看出,超构材料在降低结构厚度方面具有明显优势,其比值与基于多孔材料的结构设计相比至少提高1 个数量级,在实际应用中具有明显优势。
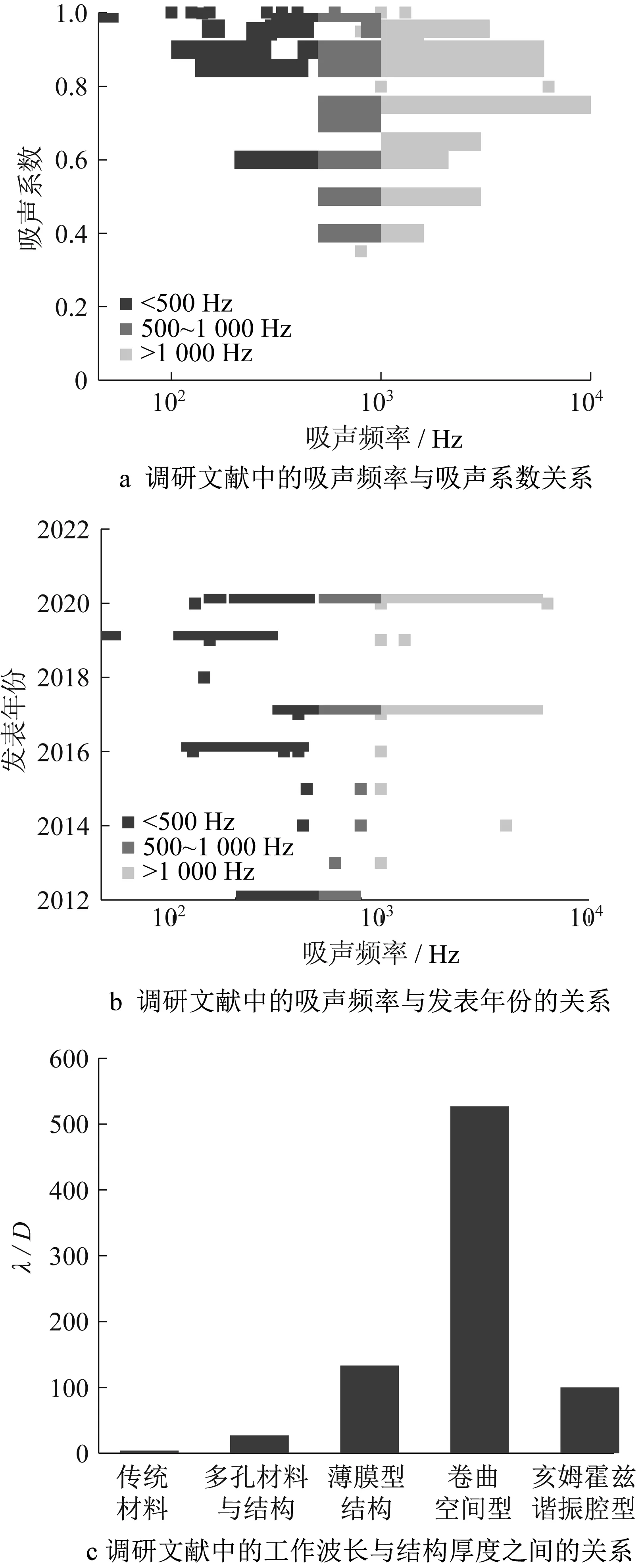
图12 参考文献中的相关参数分析Fig.12 Analysis of relevant parameters in references
3 实际应用与未来发展
3.1 实际应用
在实际应用方面,吸声结构已经取得了一定的进展。在2020年的国际消费类电子产品展览会上,日产汽车展出了基于声学超构材料的新型轻质隔声材料[76],由晶格结构和塑性薄膜构成,可有效抑制500 ~1 200 Hz宽频的噪声传播,并且比传统隔声材料轻75%,显著提高了汽车的能源利用效率。同年,马裕超工程师在基于薄膜型超构材料的降噪技术中取得突破[77],可在100 Hz 处降低7 dB 的变压器噪声。值得关注的是中国香港的静音科技集团在吸声超构材料方面的实际应用也做出了极大的贡献[78],并已实现产品化。其设计的隔声超构材料成功应用于酒店的中央空调系统[79],将中央空调的噪声由83 dB 降低到63 dB,并且不阻碍空气流通,安装方便。纵观全球,波音航空公司、丰田汽车公司、LG电子公司、雷神导弹公司以及国内深圳光启高等理工研究院等都在超构材料产业化方面取得了一定的成果[80],故吸声型的超构材料有望成为应用最广泛的超构材料。
3.2 智能化设计与应用
在基于声超构材料的结构设计上,利用智能算法进行结构优化,将多声学器件耦合,结合主被动吸声等将是吸声结构向小尺度、高性能、可调带宽发展的重要方向和手段[81]。同时,在声能吸收与采集的结构中,可将智能控制算法融入外部电路中,根据结构共振频率调整电路参数,提高系统的声能采集和吸收效率。需要解决的主要问题有:理论分析多声学器件的耦合效应、提取有效的外部环境信号分析噪声频段、自适应调控结构声阻抗等。
3.3 多种物理参数、声学结构的耦合
在可调超构材料吸声结构的设计中,引入电场、磁场等可大幅度提高吸声结构的可调能力。声波作为输入信号,将引起电场或磁场变化,其中,电场信号的变化可以通过压电材料实现,如柔性的压电驻极体薄膜[82];磁场信号的变化可由小型磁铁结合导线实现;由此实现吸声结构对外部信号变化的响应,设计可调的吸声结构。除此之外,在吸声结构的设计上,可同时引入多种声学器件,耦合多种共振模式实现宽频吸声能力。
3.4 多功能发展趋势
共振型的吸声结构在实现吸声的同时将声能转换为电能并存储[83],将是未来发展的重要方向。在工业应用领域,可为无人自主系统提供自供能,如无人机、机器人、无线传感等;在交通运输方面,可在降低高铁、飞机噪声的同时提供电力能源;在国防安全方面,可有效降低鱼雷、潜艇等声辐射,减小被探测到的风险并为设备提供能源。除此之外,吸声结构的设计已经从单通道吸声结构向双通道吸声结构发展,在吸声的同时保持空气流通,将很大程度上提高其在民用降噪领域的应用。
4 结论
在结构设计方面,以往的吸声材料设计是基于材料本身的特性设计的,比如吸声棉、穿孔板等;而现在基于超构材料概念的设计思想,可实现从吸声需求入手,通过定制多功能单元和设计人工结构实现对声能的主动调控,提高吸声结构性能;在工作频带设计方面,从单频到宽频,再到向可调带宽发展;在结构尺寸方面,从亚波长尺度到深亚波长尺度发展;在功能扩展方面,增加声能采集与通风功能;在吸声效果方面,从高效吸声到向完美吸声发展;在入射角度方面,实现从垂直入射到全角度入射的吸收。
然而,吸声型超构材料同样也面临着许多挑战。由于超构材料是根据性能指标、应用场景等需求反向设计的,因此需要逆向求解边界条件,并优化结构参数,这将增加计算的复杂程度;其次,由于超构材料是周期排布的人工序构,如果结构受到破坏和损伤,将会影响人工结构的正常功能,如何对超构材料进行有效检测是一个值得思考的问题;除此之外,目前的超构材料结构大多采用3D打印,而结构的精密程度将直接受到打印精度的制约;最后,根据不同的应用领域,超构材料面临不同的工况需求,如在轨道交通和空中客机中,受到振动、冲击、异物撞击等,并且对持久性有较高的要求;在船舶中,需承受台风、海上恶劣环境以及低温潮湿的环境;在室内应用中,受到空间的限制,并在通风、绿色环保等方面有较大要求,故如何确保超构材料在不同工况下的工作效率也是其面临的挑战。
作者贡献声明:
潘永东:构思论文框架,指导论文写作与修改。
宋 潮:完成论文初稿的写作和修改。
赵金峰:指导理论部分分析和论文写作、修改。
张晓青:指导论文写作与修改。

