Adaptive modification of turbofan engine nonlinear model based on LSTM neural networks and hybrid optimization method

Yanhua MA， Xian DU， Ximing SUN

a School of Microelectronics， Dalian University of Technology， Dalian 116024， China

b Key Laboratory of Intelligent Control and Optimization for Industrial Equipment， Ministry of Education， Dalian University of Technology， Dalian 116024， China

c School of Control Science and Engineering， Dalian University of Technology， Dalian 116024， China

KEYWORDS Hybrid optimization;Long short-term memory;Model modification and testing;Sensitivity analysis;Turbofan engines

Abstract An accurate and reliable turbofan engine model which can describe its dynamic behavior within the full flight envelop and lifecycle plays a critical role in performance optimization， controller design and fault diagnosis. However， due to the performance differences caused by the tolerance of engine manufacturing and assembly， and performance degradation during continuously stringent environmental regulations，the model accuracy is severely reduced.In this paper，an adaptive modification method of turbofan engine nonlinear Component-Llevel Model (CLM)based on Long Short-Term Memory (LSTM) Neural Network (NN) and hybrid optimization algorithm is pro-posed. First， a dynamic compensator with a combined LSTM NN architecture is constructed to compensate for the initial error between the experimental data and CLM of a turbofan engine under health condition. Then， a sensitivity analysis approach based on the entropy coefficient and technique for order preference by similarity to an ideal solution integrated evaluation is developed to choose the unmeasurable health parameters to be adjusted.Finally， a parallel hybrid optimization algorithm is developed to complete the adaptive model modification when the performance degrades.The proposed method is verified on a military low-bypass twin-spool turbofan engine， and the experimental results show the effectiveness of the proposed method.

1. Introduction

As the power plant of commercial and military aerocraft， turbofan engine is a typical complicated nonlinear system which operates under varying conditions. An accurate and reliable turbofan engine performance model which can describe its dynamic behavior within the full flight envelop and lifecycle plays a critical role in simulation verification for the performance optimization，control scheme design and fault diagnosis strategy. However， due to the tolerance of manufacturing and assembly within the same fleet，and most importantly，the performance degradation caused by continuously stringent environmental regulations， the model would become less accurate.In practical engineering， model modification for a specific turbofan engine is realized by manually tuning the relative variations of the flow and efficiency factors of each component in the nonlinear component-level performance model，which are commonly defined as the health parameters. The health parameters are unmeasurable and often adopted to reflect the performance degradation of turbofan engine. Then，by comparing the difference between the outputs of performance model and experimental data， we can find out whether the model is successfully modified. This procedure is also considered to be an inverse modeling optimization process.In the past decades， a number of studies have sought to achieve the model modification.Roth et al.presented a minimum variance estimator algorithm based optimization method for performance adaption of a turbofan engine.Kong and Ki suggested a scaling method based on system identification method.Refs. 7–10 used a genetic algorithm to search for an optimal set of health parameters，and furthermore， particle swarm optimization， least square algorithm， and even scaling functions were adopted. Despite of the progress and extensive application， there are still some problems which might deteriorate the modification accuracy.

First， even though the turbofan engine is under healthy condition， there always exists an initial error between its performance model and experimental data due to the tolerance of manufacturing and assembly.That also explains the performance variations of each turbofan engine within the same fleet.During the practical model modification， this error is often neglected.However， as shown in Fig. 1， it has been figured out that the initial error also has a great impact on model accuracy even though the turbofan engine is completely healthy.Recently， a direct compensation of the initial error has been studied by Least Square Support Vector Machine (LSSVM).That is，an LS-SVM model is used to describe the initial error directly.It is noticeable that due to the unneglectable noise existing in the initial error with a small amplitude， accuracy of the direct compensation will be severely reduced.

Second， there are mainly 10 unmeasurable health parameters in the turbofan engine.In fact，not all of them are strongly related to the measurable performance parameters， which are the outputs of the model. Usually， a step-response method is used to select the related health parameters，that is，decreasing each health parameter by 1%， and calculating the variations of measurable performance parameters through the model.Then， the most related health parameters will be selected according to the amplitude of these variations.However， the relationship between the measurable performance parameter and health parameter might be nonlinear or even non-monotonic. For example， if we increase the mass flow factor of a turbofan engine performance model from 0.85 to 1.1 by a step of 0.01， that is 0.85， 0.86，...， 1.1， respectively and keep the other health parameters unchanged， the corresponding measurable high-pressure rotor speed can be obtained through the model. The relationship between mass flow factor and high-pressure rotor speed is depicted in Fig.2，which is non-monotonic，obviously.This example indicates that the traditional sensitivity analysis by a fixed step of 1% is not appropriate for such situations. Therefore， instead of a fixed step， each health parameter should be described by a series of amplitude which covers its effective value. Thus，each corresponding measurable performance parameter pis depicted as an interval number [p， p]. Therefore， how to select the related health parameters based on interval numbers forms a challenging task.

Fig. 2 Relationship between mass flow factor of fan and highpressure rotor speed.

Fig. 1 Initial error of compressor outlet pressure P3 and low-pressure turbine outlet temperature T5 at 2 km and Ma = 0.42 for a turbofan engine.

Moreover， once the related health parameters are selected，an optimization algorithm is implemented so that the measurable performance parameters of the model are consistent with the experimental data.Thus， model modification is transformed to a high-dimension optimization problem. The optimization algorithm with fast convergence rate， high accuracy and the ability to deal with high-dimension data has become an increasingly important issue. Recently， swarm intelligent optimization algorithms are commonly used in this procedure.Nevertheless，it is inevitable that each optimization algorithm has demonstrated its own advantages and drawbacks. Thus， efficient hybrid optimization algorithm should be developed to deal with this problem.

To this end， in this paper， we try to provide a model modification method for the turbofan engine performance model.Compared with the existing literatures，the main contributions of this paper are as follows:

(1) To the best of our knowledge， it is the first time that a dynamic compensator based on Long Short-Term Memory (LSTM) Neural Network (NN) is proposed to deal with the initial error between the performance model and experimental data under healthy condition of turbofan engine， which is severely polluted by the nonstationary measurement noise.

(2) To improve the sensitivity analysis method in dealing with the non-monotonic relationship between health parameters and measurable performance parameters， a new approach based on entropy coefficient and Technique for Order Preference by Similarity to an Ideal Solution (TOPSIS) integrated evaluation is developed to solve the decision problem of multi-index interval numbers.

(3) Instead of the single intelligent optimization algorithm，a parallel hybrid optimization algorithm with global search ability and fast convergence speed is proposed to complete the adaptive model modification.

The remainder of this paper is organized as follows: Section 2 describes the model modification problem. Section 3 presents our methodology. The application case and its corresponding results are demonstrated in Section 4.Section 5 concludes the paper.

2. Problem formulation

In this section， we first introduce the model of the low-bypass twin-spool turbofan engine， and describe the model modification problem subsequently.

2.1. Component-level model of turbofan engine

The structure of the low-bypass twin-spool turbofan engine is shown in Fig. 3， with components of intake， fan， compressor，combustor， High-Pressure Turbine (HPT)， Low-Pressure Turbine (LPT)， bypass， mixing chamber， afterburner， and nozzle.

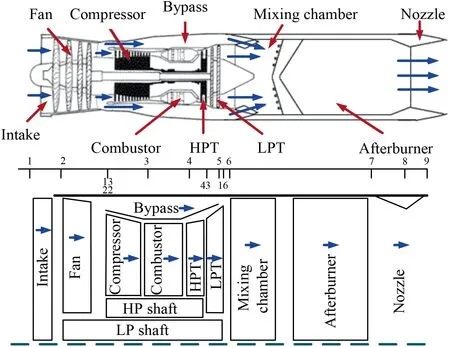
Fig. 3 Schematic diagram of turbofan engine with crosssectional number.

As a performance model， the Component-Level Model(CLM) of the turbofan engine is most extensively used. For model construction， first， each component of engine is modelled based on dynamic aerothermodynamics principles， rotor dynamics， etc. Then， by the co-operating equations， including the flow continuity equations， pressure balance equations and power balance equations or shaft dynamics equations， the cooperation relationship among the component models is established. Usually， by using of the Newton-Raphson method to solve the formulated nonlinear co-operation equation set， we can finally derive the measurable performance parameters，such as the rotor speeds， pressures and temperatures in the flow path， and the unmeasurable parameters， such as thrust.Both of the measurable and unmeasurable performance parameters are the outputs of CLM and determined by the health parameters.

A detailed description of the CLM can be referred to in Ref. 20 and Fig. 4 gives the flowchart of turbofan engine model computation. Pand Tstand for the atmospheric pressure and temperature at H km above sea level， respectively; Ma denotes the flight Mach number; Wrepresents the fuel flow of combustor; ais the area of nozzle throat;e－eindicate the flow continuity equation of HPT inlet，flow continuity equation of LPT inlet，static pressure balance equation between internal duct exit and the bypass duct exit， and total pressure balance equation at nozzle throat， respectively.

2.2. Problem statement

The measurable performance parameters of the military lowbypass twin-spool turbofan engine CLM concerned in this study are measurements of its flow path，including the relative corrected speed of the low-pressure rotor nand high-pressure rotor n， outlet pressure Pof the compressor and outlet temperature Tof the LPT， which are represented by a vector p = [n， n， P， T]∈R.

According to the above subsection， p is considered to be a function of ambient and operating condition parameters u = [P， T， H， Ma， α， α， W， W， a]∈R， which determines the power level.αand αare the guide vane angle of fan and compressor， respectively; Wrepresents the fuel flow of afterburner.

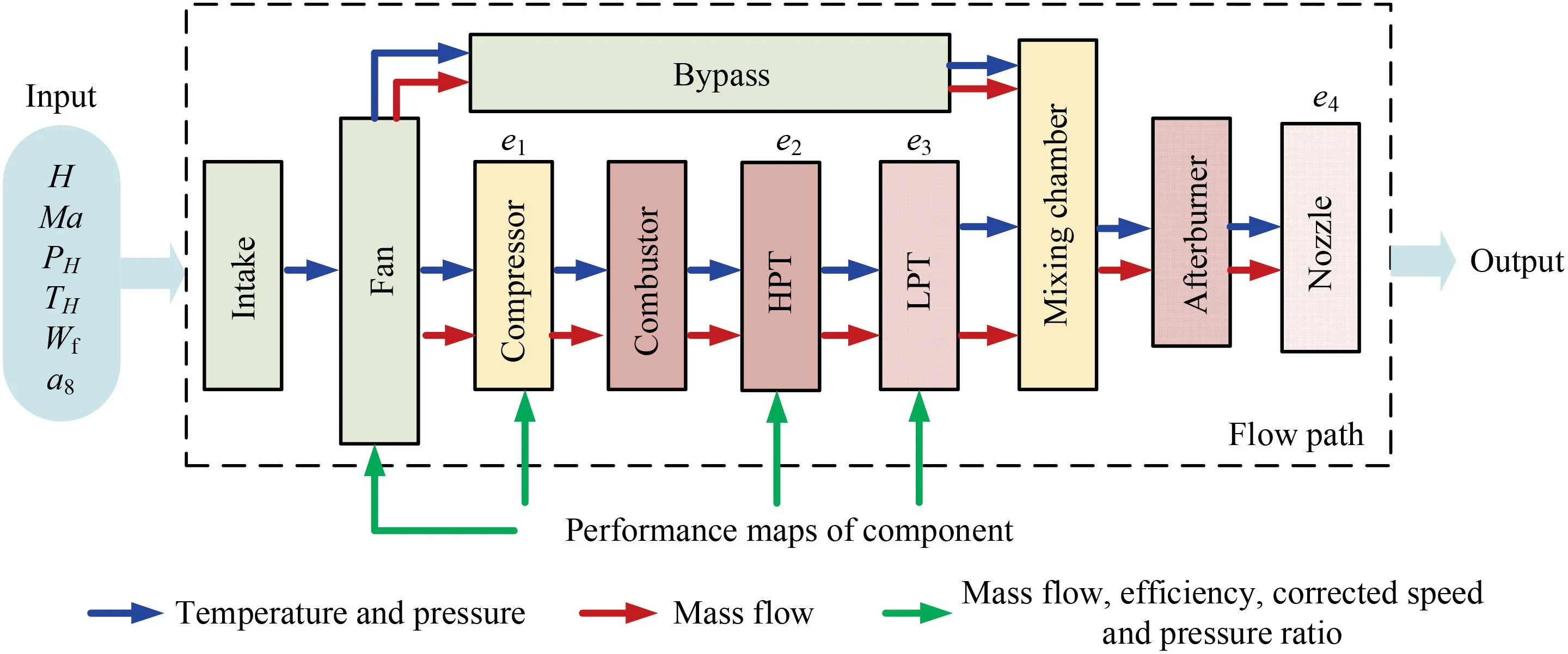
Fig. 4 Schematic diagram of computational interaction of turbofan engine model.

The unmeasurable health parameters that we focus on in this study are represented by a vector x＊ as

x＝ ［W，W，W，W，η，η，η，η，π，π］∈Rwhere W， W， Wand Wdenote the corrected flow of inlet and outlet of compressor and LPT， respectively; η，η， ηand ηstand for the efficiency of fan， compressor，LPT and HPT，respectively;πand πare the pressure ratio of combustor and bypass， respectively.

Practically，instead of x＊，we often employ the relative variation of each health parameter， which is called normalization.Then x＊ is normalized as

To this end， the objective of this paper is to achieve the adaptive modification of turbofan engine performance model，so that:

(1) For the turbofan engine under healthy condition， a dynamic compensator based on LSTM NN is proposed to mitigate the initial error caused by the tolerance of manufacturing and assembly within the same fleet， so that the measurable performance parameter p of CLM agrees with the experimental data during the whole flight envelope.

(2) In the presence of performance degradation， x can be adaptively adjusted so that the measurable performance parameter p of CLM agrees with the experimental data during the whole flight envelope.

3. Methodology

The schematic diagram of the proposed methodology is shown in Fig. 5.

First，a dynamic compensator with a combined LSTM NN architecture is proposed to compensate for the initial error between the experimental data and CLM under healthy condition.Then，a new sensitivity analysis method based on entropy coefficient and TOPSIS integrated evaluation is developed to select the related health parameters. Finally， when the performance of turbofan engine degrades，a parallel hybrid optimization algorithm is employed to achieve the adaptive model modification.

3.1. Dynamic compensator based on neural network

3.1.1. Architecture

As mentioned in the previous section，a direct compensation of the initial error between CLM and experimental data of a turbofan engine under healthy condition as depicted in Fig.6(a)is inaccurate. Because under the varying flight conditions， there always exists noise in the experimental data.Usually，the measurable outputs are considered to be polluted by additive，nonstationary colored noise w(t)， i.e.

where yrepresent the measurable performance parameters generated by the CLM.

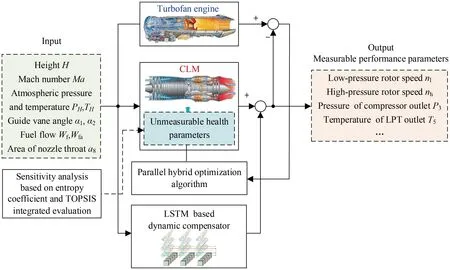
Fig. 5 Schematic diagram of proposed methodology.

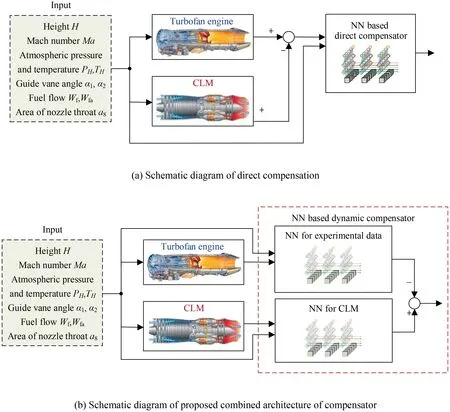
Fig. 6 Dynamic compensator based on NN.

To deal with this problem，we propose a combined architecture composed of two NNs as shown in Fig. 6(b). One NN is used to approximate the measurable performance parameters of experimental data under healthy condition，which is defined by y+w(t).And the other NN is used to approximate the outputs yof CLM. Then， instead of one NN， the initial error can be described by calculating the difference of the two NNs as follows:

Following that， the kernel of the dynamic compensator design is to select a suitable NN to achieve the sequential modeling. Recently， LSTM NN， originally introduced by Hochreiter and Schmidhuber，has been demonstrated to be one of the most efficient models when dealing with time series because of its ability to retain information about previous states of the system.Different from the traditional Recurrent Neural Network (RNN)， which is hard to learn to store information for very long time，the central idea behind the LSTM architecture is a memory cell which can maintain its state over time，and nonlinear gating units which regulate the information flow into and out of the cell.Fig. 7 illustrates a typical architecture of LSTM network， and each of its cell is constructed by forget，input，and output gates to control the flow of information through the cell and accordingly the output of the cell.

To start with， the forget gate determines the information which will be abandoned.The combination of input of the current time xand output of the previous time his used for calculating the output of forget gate fby a nonlinear transformation as

where^iand istand for the input and output of the input gate，respectively， and W， R， and bare input gate’s input weights，recurrent weights and bias， respectively.

Meanwhile， a nonlinear function φ， usually chosen to be a tanh function， creates a vector of new candidate value φ， and updates the cell state Cas

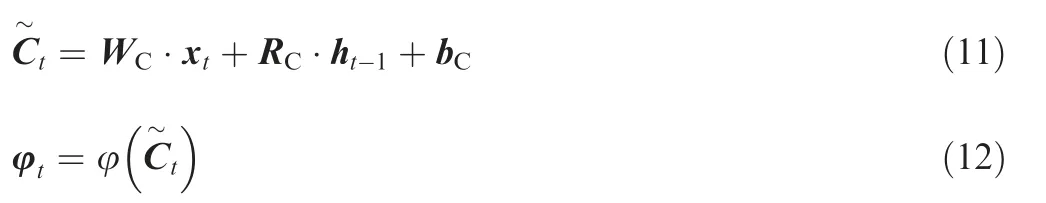
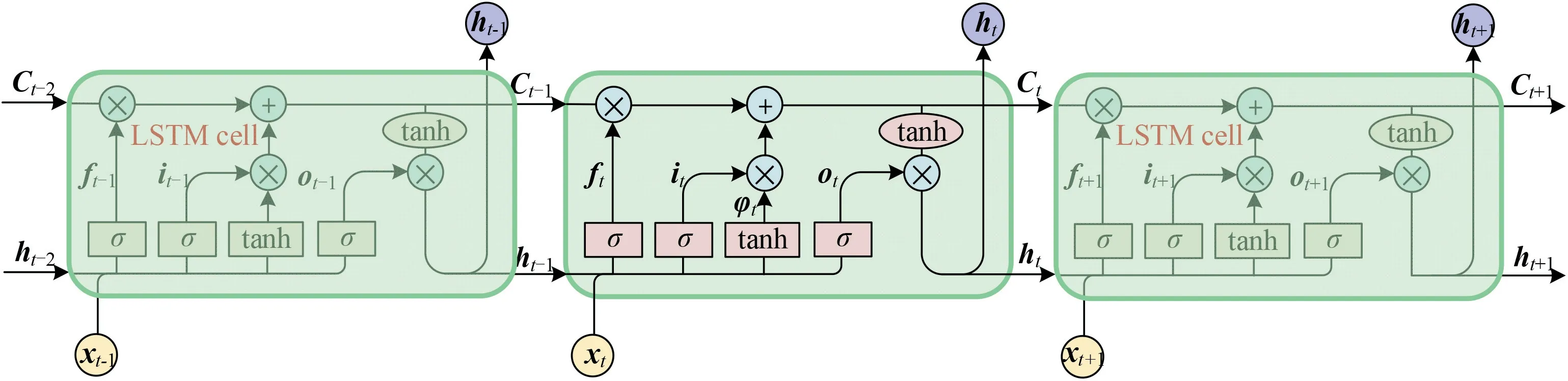
Fig. 7 Schematic diagram of LSTM layer.

where^oand odenote the input and output of the output gate，respectively， and W， Rand brepresent the weights， recurrent weights and bias of output gate， respectively.

3.1.2. LSTM neural network based dynamic compensator

The data used in this paper are the raw production data of actual turbofan engine， so it is inevitable to include noise as influencing factor. Thus， data preprocessing scenario should be incorporated.

First， to deal with outliers in the experimental data， we adopt a distance-based outlier rejection over the time series.Then， we used mean and standard deviation to normalize the experimental data d as

d＝ （d－dE）／d

where subscription i stands for the ith measurable parameter;‘‘mean” and ‘‘std” represent the mean and standard deviation of the experimental data， respectively.

For both experimental data and CLM data under healthy condition，we construct the dataset Ω=[u，p]，and randomly make 70% of it to be the training dataset， the left 30% to be the test dataset. Specifically， for input u = [P， T， H， Ma，α， α， W， W， a] of each individual transient state， that is，each acceleration or deceleration process， P， T， H and Ma indicate the operation mode of the turbofan engine. Thus， by the one-hot encoding， the operation mode label is constructed to distinguish the complex working conditions.

In addition， for each LSTM NN in the dynamic compensator，a loss function is designed to be a function of error，that is， the NN is trained by minimizing the error between its output and the experimental or CLM data in the training dataset.The loss function F is defined as

The initial acc is set to be infinite， and then max(abs(y－y)) describes the maximal distance between the network and the experimental data.When it is smaller than that of the last time，acc is updated and the current parameters of NN are considered to be the optimal training model.

3.2. Sensitivity analysis

A sensitivity analysis is used to identify the most related parameters to the measurable performance parameters. To deal with the drawbacks of the traditional step-response method， a new approach based on entropy coefficient and TOPSIS integrated evaluation is developed to solve the decision problem with multi-index interval numbers. When the weight information is completely unknown， the information of mid-point and width of interval numbers is used to solve the weight coefficient objectively， so as to avoid decisionmaking mistakes which are caused by subjective weight coefficient.And then，the entropy coefficient and TOPSIS integrated evaluation are adopted to solve the problem of interval numbers decision matrix， which will reduce the decision-making errors.

Actually，the upper and lower bound of each health parameter xdetermine the domain of the search space. By proper selection of the bounds， we decrease each health parameter by a 0.05 step from xto x， i = 1，2，...，m， at a steady point， with the other ones unchanged， and denote the corresponding measurable performance parameter by p， where k = 1，2，...，n is the kth measurable parameter， j = 1，2，...，[(x－x)/0.05]. Further， the relative error at the steady point is calculated by

where 0 ＜η ＜1 is the balance factor.

And the entropy weight wand the entropy weight decision value vare calculated as

The comprehensive decision value F=α(v+c)，where α is the amplification coefficient.Fis ranked by ascending order，and the former four are chosen to be the most related health parameters.

3.3. Hybrid optimization algorithm based model modification

The scheme of hybrid optimization algorithm based model modification is shown in Fig. 8. After comparing the experimental data of a turbofan engine with the compensated CLM model under certain operating condition， the optimization algorithm is adopted to update the health parameters adaptively so that the difference between the model and the experimental data is converged to zero.

Fig. 8 Scheme of hybrid optimization algorithm based model modification.

The adaptation error for each target performance parameter is defined by the relative difference between the actual turbofan engine and CLM as where αare the weighting factors according to the importance of performance parameters. In this paper， all of the M performance parameters are considered to be equally important，and α= 1(i = 1，2，..，M).

As has been known，even though Particle Swarm Optimization(PSO)algorithm is prominent for its rapid searching capability， to solve a complex optimization problem， it becomes easily trapped in local optimum. Compared to PSO， the Cuckoo Search (CS) algorithm is prominent in global search capability due to the high randomness of Le´vy flight.However，the main drawbacks to it are slow convergence speed and low accuracy owing to its weak local search ability.Therefore，accounting for the limitation of a single bionic swarm optimization algorithm， a parallel hybrid optimization algorithm consists of PSO algorithm with an Adaptive Dynamic Coefficients (ADCPSO) to improve the global search ability and the Local Search Ability Enhanced CS (LSAECS) algorithm is proposed.

3.3.1. Adaptive dynamic learning particle swarm optimization algorithm

where tis the total iteration number， t is the current iteration number， and ωand ωare the initial and end value of ω， respectively.

In addition， cand care the cognitive and social constants， which determine the movement steps of particles. In PSO， usually c= c= 2， which means that the importance of local and global search ability are constant. However， as discussed before， they should be dynamic. Thus， an adaptive update of cand ccan be provided as follows:

3.3.2. Local search ability enhanced cuckoo search algorithm

The LSAECS algorithm also starts with the initialization procedure， that is， randomly generating a population of N initial solutions corresponding to an egg， and supposing the dimension of searching space to be D.Then in the subsequent searching procedure， the position is updated by

3.3.3. Parallel hybrid optimization algorithm

According to the parallel hybridization， ADCPSO and LSAECS algorithms begin to share each other’s optimal individuals， that is， replace the worst m individuals by the other’s best m individuals. Then， by incorporating the advantages of both algorithms， the global search ability， convergence speed and adaptability are improved. The flowchart of hybrid optimization algorithm is shown in Fig. 9.

It is noticeable that， traditionally， the number of replaced individuals should be no larger than half size of the population to avoid receiving the original worst individuals. However，with the evolution of the algorithms， individuals of ADCPSO and LSAECS will gather inevitably. To solve the problem， in this paper， the number of replaced individuals is determined by the position of the best individuals. Specifically， if the distance between the best individuals is large，which indicates that the two algorithms are not prone to gather，the replaced number should be larger to improve the global search ability， and vice versa. The proposed algorithm can be described as follows:

Step 1.Initialization.Initialize population N and dimension of individual D.

Step 2. Parallel evolution. Optimize the health factors with ADCPSO algorithm and LSAECS algorithm simultaneously. During each iteration， the algorithm will be evolved once independently. As a result， both ADCPSO algorithm and LSAECS algorithm own their optimal individuals.

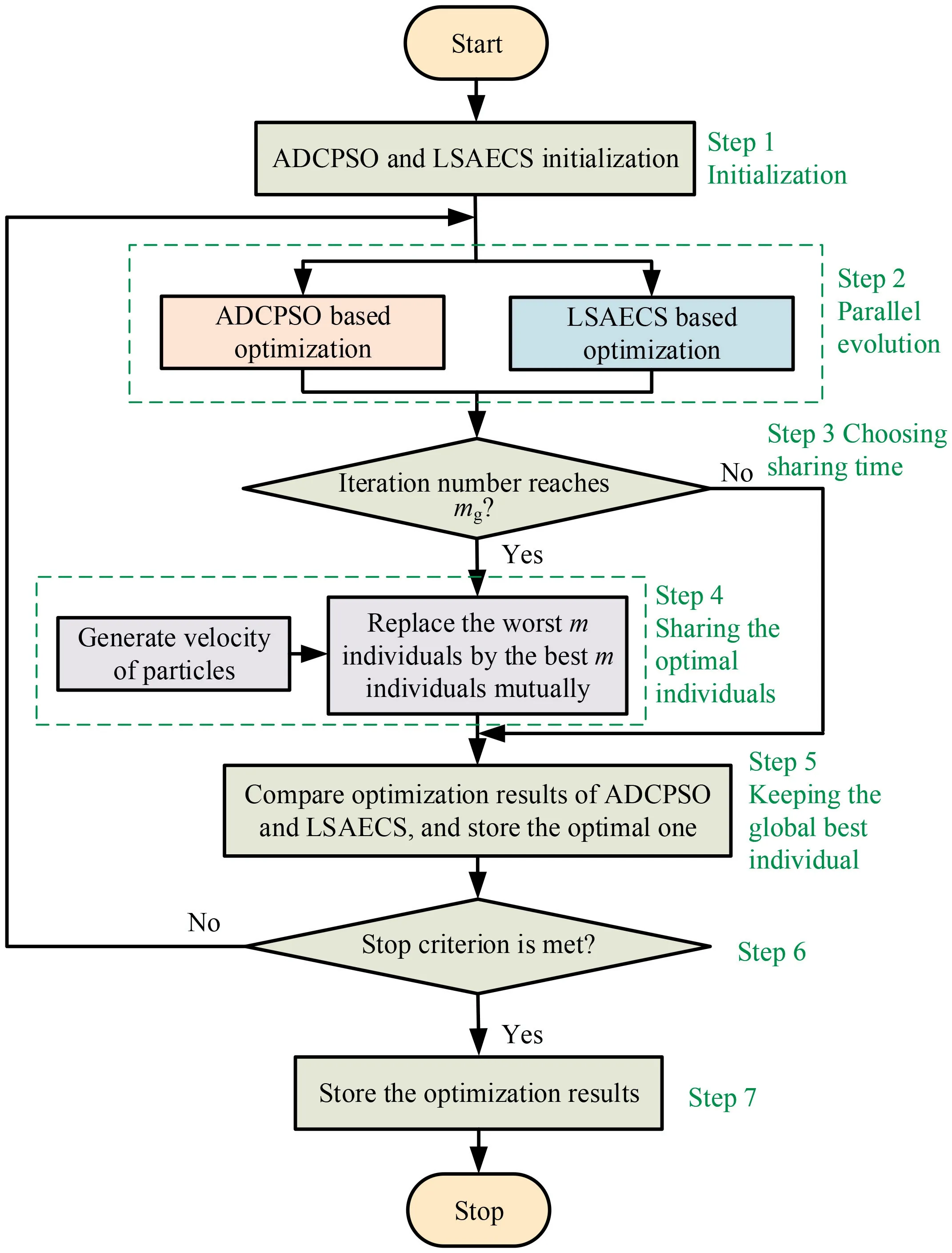
Fig. 9 Flowchart of hybrid optimization algorithm.

Step 3. Deciding sharing time. When the preset iteration generation mis met，which can be adjusted during the optimization process，the hybrid algorithm begins to work，and go to Step 4; otherwise， go to Step 2.

Step 4. Sharing the optimal individuals. Calculate the replaced individual number m(t) at the tth iteration by

Besides， it is noticeable that in LSAECS， there are only position and fitness appearing in the algorithm， while in ADCPSO， the individual velocity should also be considered.In order to generate the velocity of the optimal individuals in LSAECS， a velocity series is generated by logistic-map chaos model as

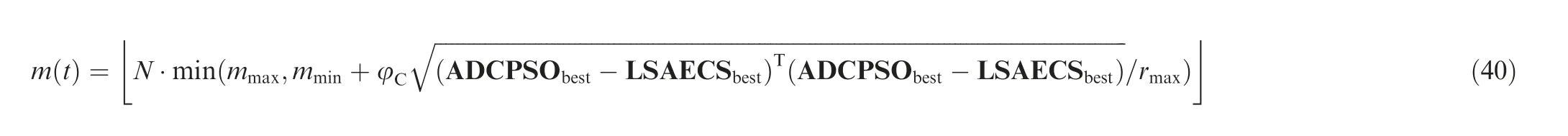
where m＜0.5 and 0.5 ＞m＞0.1 stand for the maximum and minimum exchanging coefficient， respectively; φrepresents the proportion control parameter; rdenotes the maximum Euclidean distance of the searching space;ADCPSOand LSAECSare the optimal individual position of the current generation of ADCPSO and LSAECS，respectively; ■·」 means to round down.

Replace the worst m(t)individuals of the two algorithms by each other’s best individuals.

where θ is the control coefficient and often chose to be 4，which brings the model into a complete chaos state. And during the replacing process，position and fitness can be replaced directly.Step 5. Keeping the global optimal individual. After each evolution，compare the objective functions of the optimized best individuals of ADCPSO and LSAECS， and keep the best individual.

Step 6.If the stop criterion comes，which is the accuracy or the maximum iteration number， go to Step 7; if not， go to Step 2.

Step 7. Store and visualize the best candidate solution.

The fitness function of the optimization algorithm is often defined as

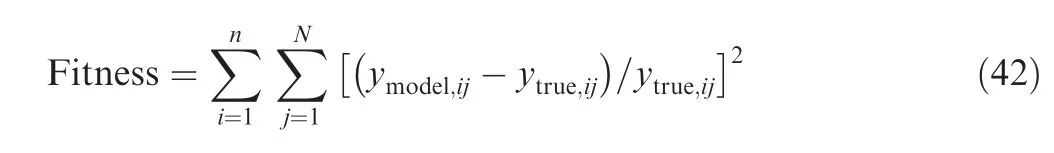
where yand yrepresent the jth sample of the ith measured output generated by CLM and corresponding experimental data， respectively. However， it is noticeable that when the proposed parallel hybrid optimization algorithm is implemented together with the LSTM-based dynamic compensator shown in Fig. 4， the fitness function should be modified to

where yand ystand for the jth sample of the ith output of the LSTM model for CLM and experimental data，respectively.

4. Experiments and results

In this section， the performance of our proposed adaptive modification method is demonstrated in comparison with the existing techniques which have been extensively used.

4.1. Experimental data

A total of 130 sets of experiments have been carried out on a military low-bypass twin-spool turbofan engine， which contains 77 sets acceleration (from the idle to intermediate state)and 53 sets deceleration (from the intermediate to idle state)at different altitudes， Mach numbers and flight cycles. Among them， 12 sets acceleration and 10 sets deceleration experimental data are considered to be under healthy condition. The basic information of the experimental dataset is listed in Table 1.

Split the original 22 datasets under healthy condition into 70% for training and 30% for testing. And in each set， there are total 10 sampled signals which are listed in Table 2.In this paper，four measurable parameters n，n，P，Tare chosen to be the performance parameters， that is， the four measurable parameters generated by CLM which should agree with the experimental data in the full envelope.

Notably， before the modification procedure， the rotor speeds nand nare transformed to the relative corrected speedNand N， respectively， and other parameters are also transformed to the relative values.

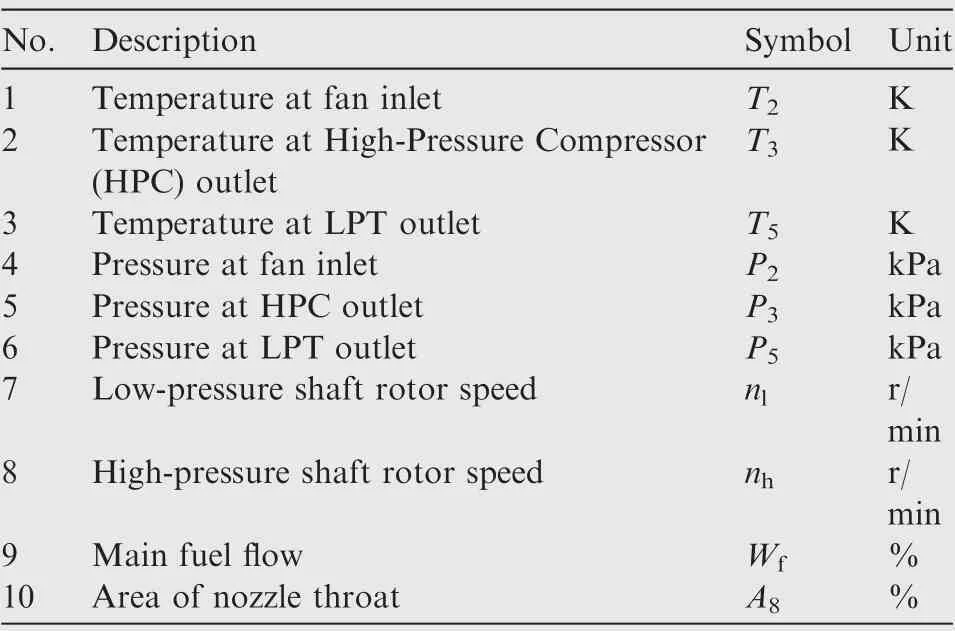
Table 2 Description of turbofan engine variables.

The following model modification verification has been run on a PC with Intel Core i5 6400 (2.7 GHz) CPU， 4 GB memory， Microsoft Windows 7 operation system and an NVIDIA 1080Ti GPU. Programming language is Python 3.6 with deep learning library PyTorch (0.4).

4.2. Performance evaluation of dynamic compensator

First， in order to evaluate the effectiveness of the LSTM NN based dynamic compensator， we choose the classical Mutiple-Layer Perceptron (MLP) and RNN based dynamic compensator for comparison.Except for the same input and output layer， the MLP contains 6 full connected layers with dimension of (2048， 2048， 4096， 4096， 2048， 2048) and 5 activation layers with ReLU activation function， while the RNN includes 4 RNN layers with 10 hidden nodes and ReLU activation function followed by an output layer. The architecture of LSTM NN is the same as that of RNN， using LSTM layer instead，and there are 16 LSTM cells.The stochastic gradient ADAM optimizer is applied to train the NNs with 500 iterations. The learning rate is 0.001 and decay weight λ is 0.1. In addition， the loss function has been defined in Section 3.1.2， so does the NN model optimization method.

To begin with，we adjust the network architectures of NNs in three ways， which are increasing the hidden layers， using tanh as the activation function， and iteration number decay based learning rate， which is described as

where the initial learning rate is 0.001，s is the decay steps with[i，i，i]=[20，100，300]，and γ=2.The optimization resultsof the three types of NNs are listed in Table 3， which is presented by iteration number/Mean Square Error (MSE).

Table 1 Basic information of experimental dataset.

Table 3 Neural network optimization results.

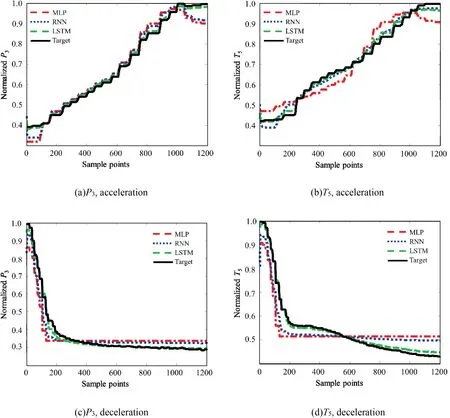
Fig. 10 Comparison of compensators based on three types of NN (H = 2 km， Ma = 0.48).

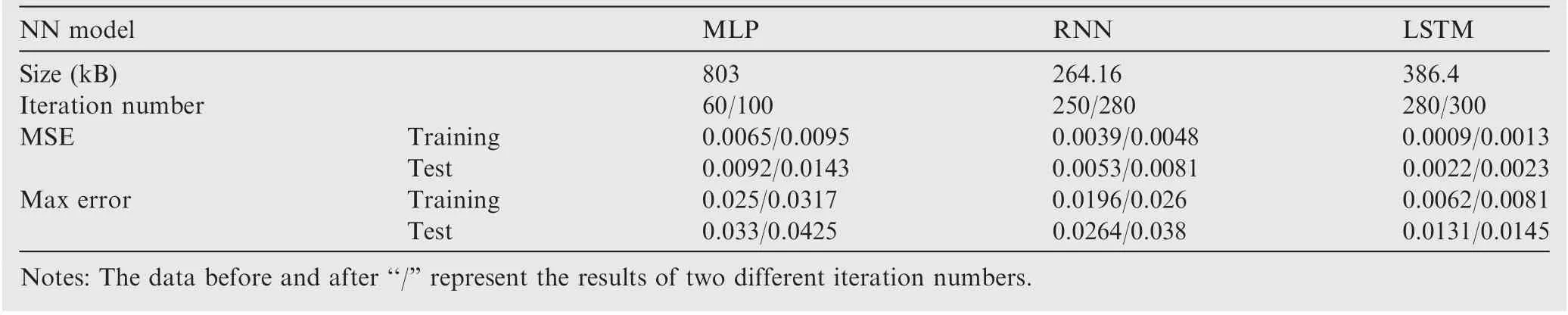
Table 4 Comparison results of compensators based on three types of NN.

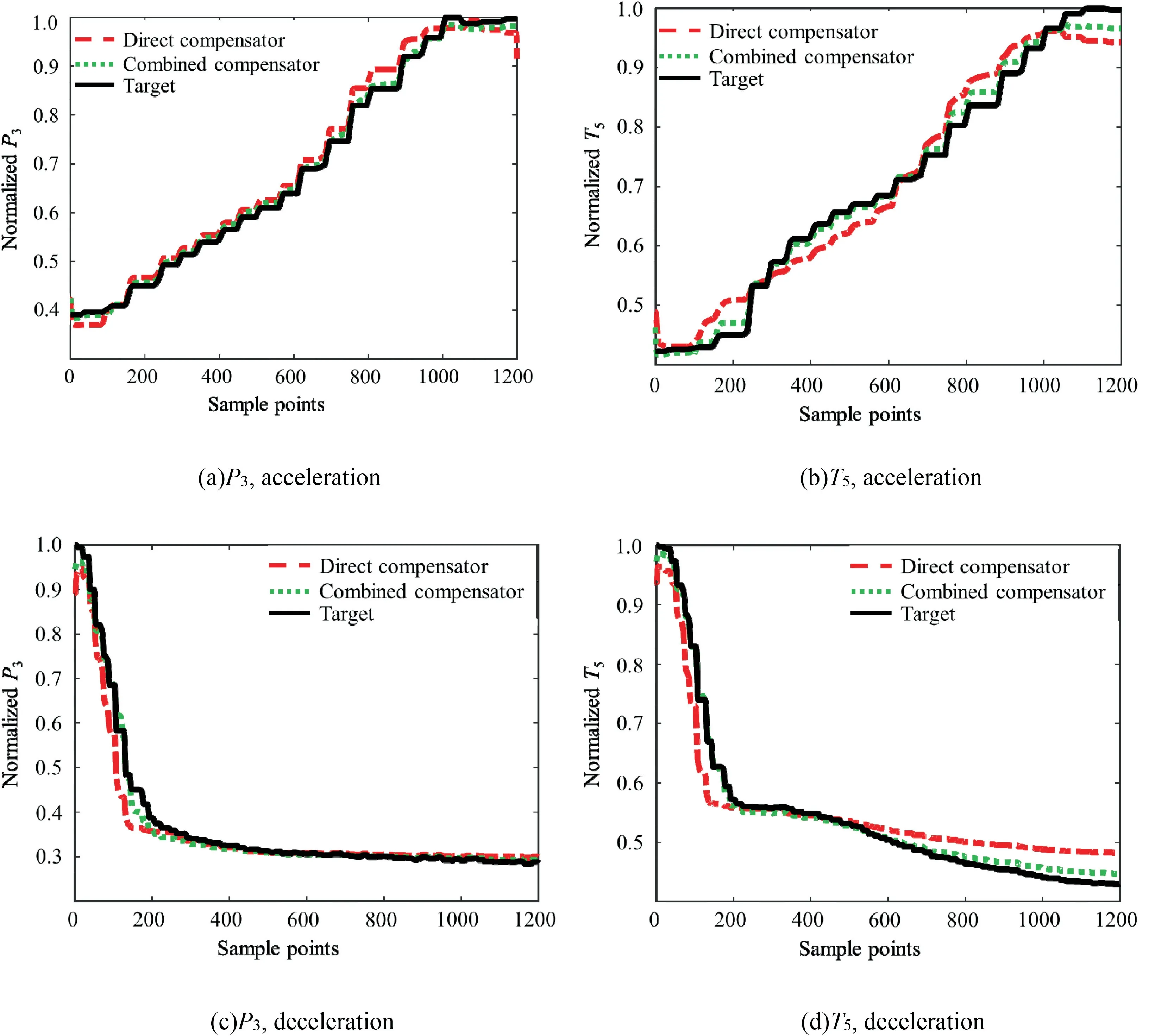
Fig. 11 Comparison of direct compensator and combined compensator based on LSTM (H = 2 km， Ma = 0.48).

It can be concluded from Table 3 that there is no significant influence of increasing the hidden layer， but increasing the training time and computation burden instead. Moreover， a tanh activation function reduces the accuracy and increases the training time. However， the iteration number decay based learning rate can accelerate the convergence rate prominently.As a result， we choose the number of hidden layer to belayer + 1， ReLU activation function and iteration number decay based learning rate.

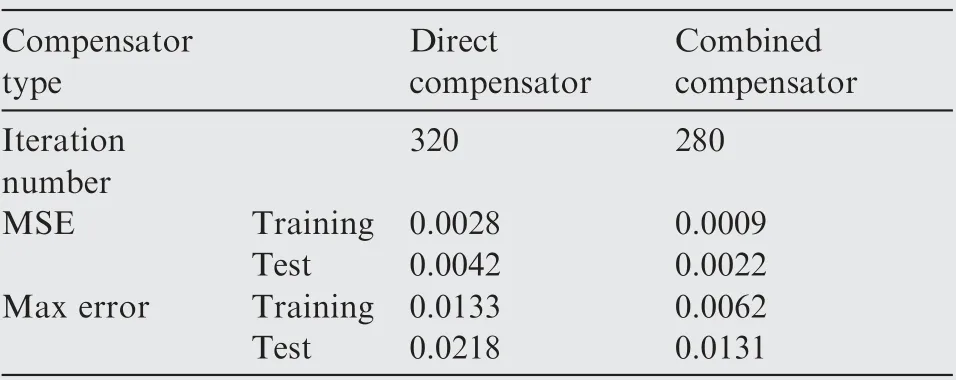
Table 5 Comparison results of initial error between two types of compensator.

Further， since there are two distinct working conditions including acceleration and deceleration procedure， the comparison results of NNs at H=2 km and Ma=0.48 are shown in Fig. 10， with both the average training and test accuracy shown in Table 4.It is noticeable that MLP，RNN and LSTMdemonstrate clearly different performance in dealing with time series modeling of measurable parameters. Even though the data fitting ability is acceptable for MLP， its overfitting effect is unacceptable. It loses the accuracy of deceleration sample and the end of the acceleration sample， because the network architecture is not suitable for time series although the input regression is adopted. RNN performs much better than MLP. However， the error is bigger than that of LSTM due to its incompetence to describe the detail of the sample.Besides， LSTM overwhelms the other two networks in both model size and iteration number.

Table 6 Description of health parameters.

Table 7 Optimization scale and decision value.

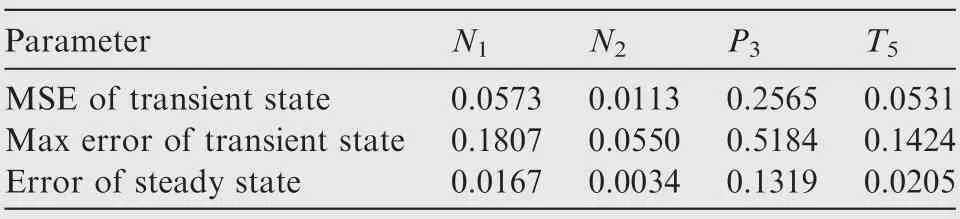
Table 8 Original transition state error.

Finally， comparison results of the direct compensator and the proposed combined compensator both based on LSTM NN at H=2 km and Ma=0.48 are provided in Fig.11，with both average training and test accuracy shown in Table 5.The iteration number for each compensator have been optimized by over 20 tests and then set to be 320 and 280 respectively.It can be seen from the results that even though the LSTM NN based direct compensator is more accurate than the MLP or RNN based combined compensator， the LSTM NN based combined compensator is more suitable for dealing with the initial error.

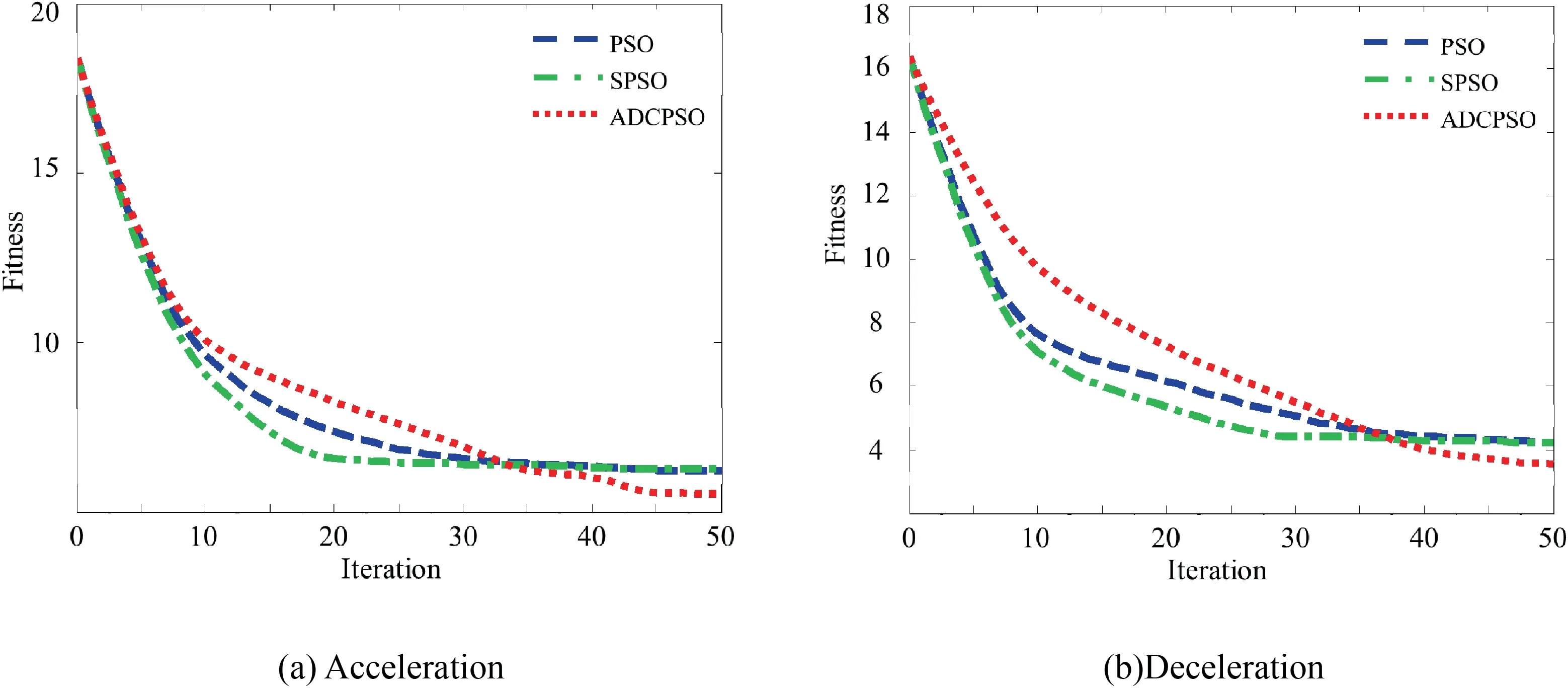
Fig. 12 Fitness of PSO， Stochastic Particle Swarm Optimization (SPSO) and ADCPSO.

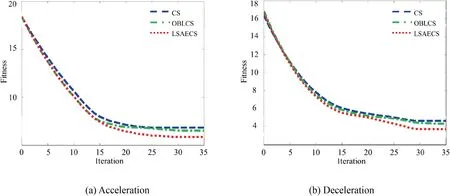
Fig. 13 Fitness of CS， Opposition-Based Learning Cukoo Search (OBLCS) and LSAECS.

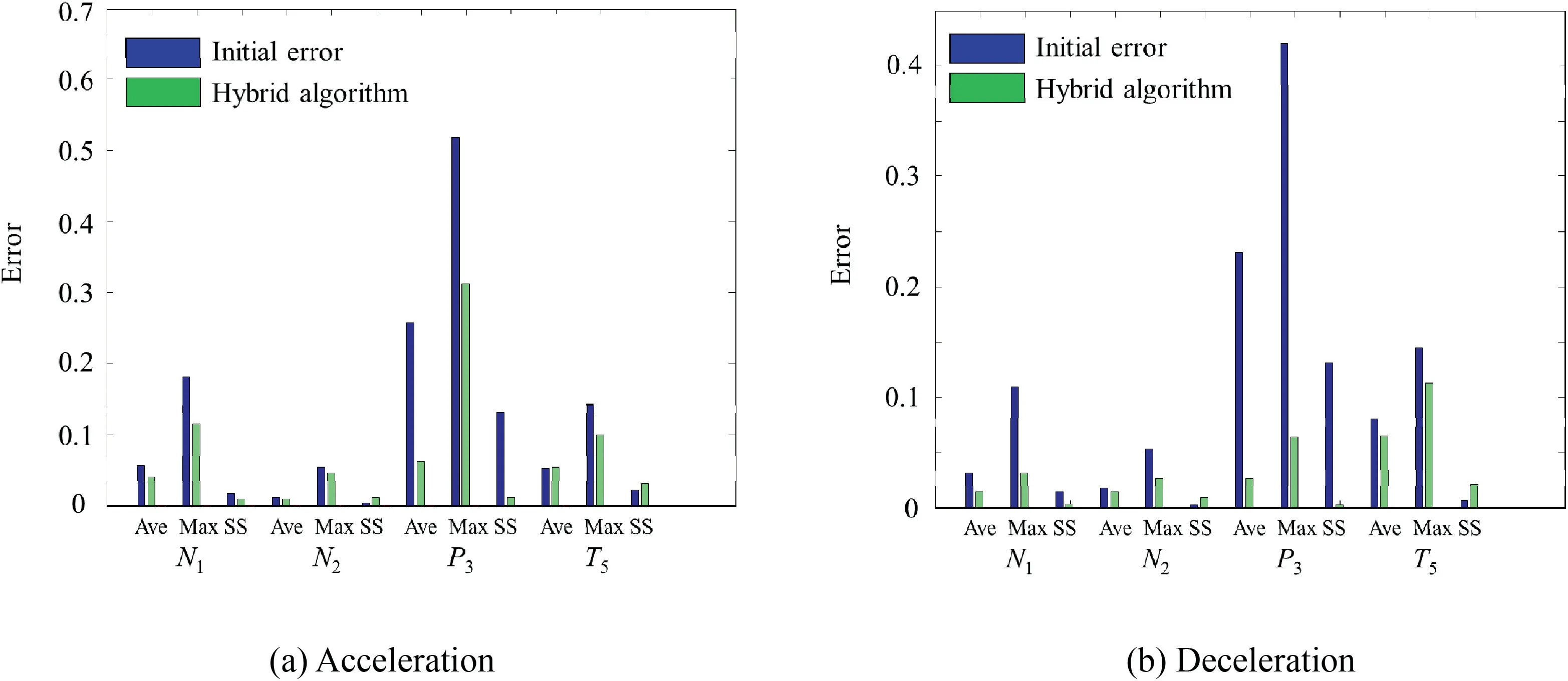
Fig. 14 Average (Ave)/maximum (Max)， Steady-State (SS) error variation of acceleration and deceleration procedure.

Table 9 ADCPSO algorithm performance.

Table 10 LSAECS algorithm performance.

Table 11 Hybrid algorithm performance.

4.3. Performance evaluation of hybrid optimization

First，a method based on entropy coefficient and TOPSIS integrated evaluation as described in Section 3.2 is developed to solve the decision problem of multi-index interval numbers so as to decide the related health parameters， which is shown in Table 6. The upper and lower bounds for each parameter are listed in Table 7. Then， by the proposed sensitive analysis method， we choose the most related four parameters Q， Q，Eand Qaccordingly.

To verify the proposed hybrid optimization method，experimental data with performance degradation (55 sets acceleration and 43 sets deceleration) are used. And modification results of ADCPSO and LSAECS algorithms are also listed together with the hybrid optimization method for comparison.The fitness function‘‘Fitness”is defined as a summation of the weighted measurable parameters:

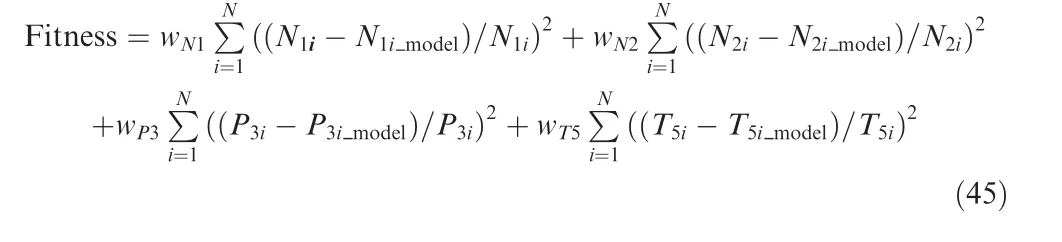
where subscripts‘‘i”and‘‘i_model”represent the ith sample of experimental and CLM data，respectively.And in our tests，the weights of N， N， Pand T， which are defined as w， w，wand wrespectively， are preset to be equal. They can be adjusted according to engineering requirements， practically.

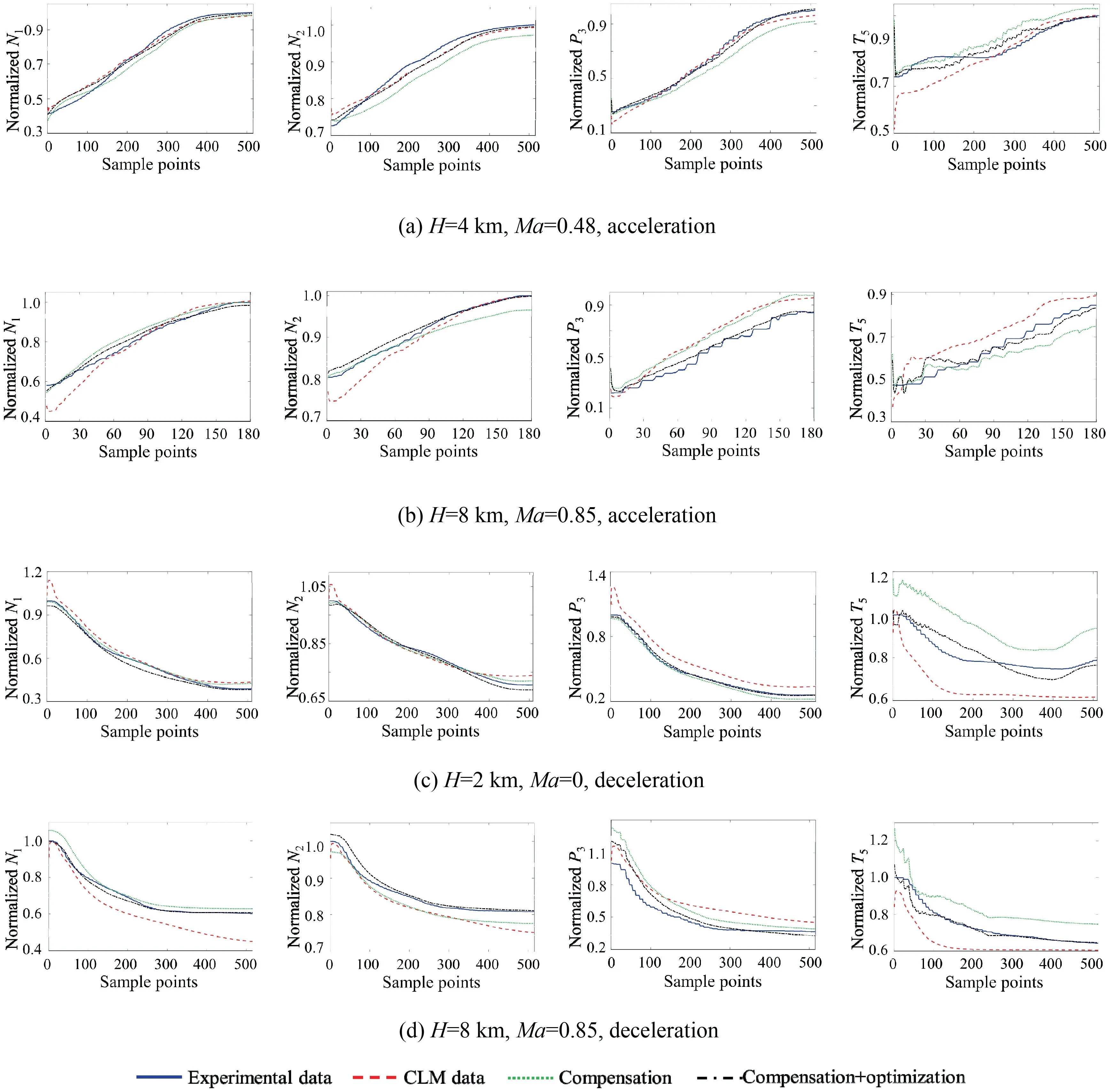
Fig. 15 Modification results under typical working conditions.

Both of the acceleration and deceleration procedures at H = 8 km and Ma = 0.27 are considered. The original transition state errors between the CLM and experimental data are illustrated in Table 8.It is obvious that there are unacceptable errors of larger than 5% during the transient state.

Finally， the proposed parallel hybrid optimization algorithm is implemented together with the LSTM NN based combined compensator. Fig. 15 and Table 12 illustrate the modification results of typical working conditions， with comparison of the experimental data，CLM data， CLM with compensation and CLM with both compensation and hybridoptimization. The modified health parameters are listed in Table 13. Besides， comparison results of the average MSE，maximum， and steady-state error are presented in Fig. 16，where max represents maximum error. It can be concluded that， after dynamic compensation and hybrid optimization，the performance of CLM model can be improved.

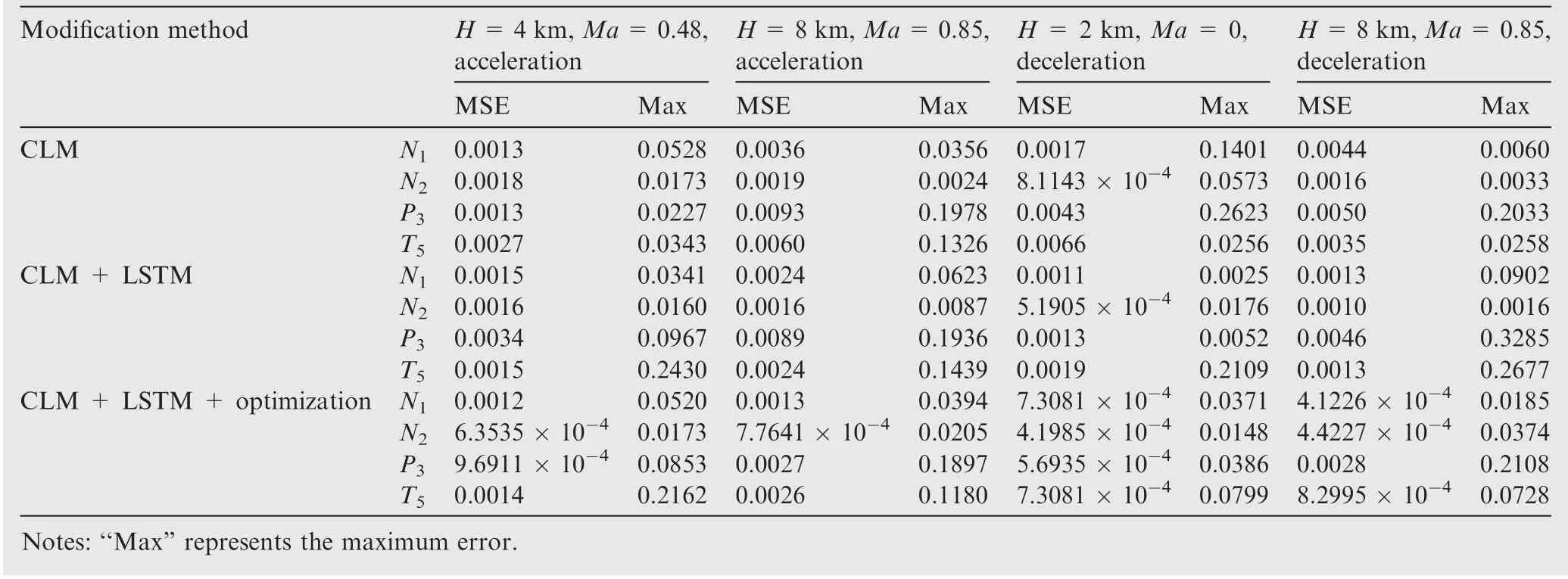
Table 12 Performance of proposed method under typical working conditions.

Table 13 Modified health parameters.

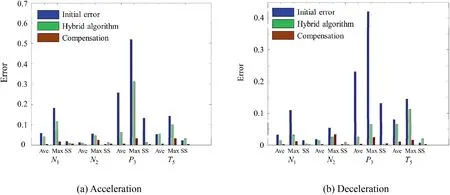
Fig. 16 Comparison of average MSE， maximum， and steady-state error of acceleration and deceleration procedure.

5. Conclusions

In this paper， an adaptive modification method for turbofan engine CLM based on LSTM NN and hybrid optimization algorithm is proposed to improve its accuracy， which is affected by the manufacturing and assembly tolerance， and performance degradation during continuously stringent environmental regulations. First， to deal with the initial error for turbofan engine under healthy condition， a dynamic compensator with combined LSTM NN architecture is constructed.Then， a sensitivity analysis approach is developed to decide the related health parameter when there exists a nonmonotonic relationship between the health parameters and measurable outputs. Finally， in order to improve the global search ability， convergence speed and adaptability of swarm intelligent optimization， a parallel hybrid optimization algorithm is proposed to complete the adaptive model modification when the performance of turbofan engine degrades. The proposed method is verified by the experiments of a military low-bypass twin-spool turbofan engine. Compared with the existing technique， the proposed method demonstrates its effectiveness.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This study was co-supported by the National Natural Science Foundation of China (Nos. 61903061， 61903059 and 61890925)，Natural Science Foundation of Liaoning Province，China (No. 2020-MS-098)， Aeronautical Science Foundation of China (No. 20200013063001) and the Fundamental Research Funds for the Central Universities， China (No.DUT20JC22).