Static magnetic field analysis of hollow-cup motor model and bow-shaped permanent magnet design

Jinji SUN， Gen XING， Xinxiu ZHOU， Haoxi SUN，*

a Research Institute for Frontier Science， Beihang University， Beijng 100083， China

b Ningbo Institute of Technology， Beihang University， Ningbo 315800， China

c School of Instrumentation and Optoelectronics Engineering， Beihang University， Beijng 100083， China

KEYWORDS Air gap flux density;Bow height;Finite element;Permanent magnet motor;Static magnetic field

Abstract The hollow-cup Permanent Magnet (PM) motors have the characteristics of low power consumption， and are widely used in the aerospace field. At present， the tile-shaped PMs used by hollow-cup PM motors have poor sinusoidal characteristics of the air gap magnetic flux density waveform，which will cause torque ripple.The existing method for improving the air gap magnetic flux density waveform is not very effective when applied to hollow cup，a special motor with no stator core and large air gap.A bow-shaped PMs structure is designed for the hollow-cup motor in this paper.First，the equivalent surface current method is used to calculate the analytical formula of the static magnetic field of the model. Then， the Finite Element (FE) method is used to calculate the static air gap flux density waveform of conventional tile-shaped PMs and bow-shaped PMs with different bow heights，and the corresponding harmonics and sine distortion are obtained by Fourier decomposition. The simulation results show that the bow-shaped PMs can effectively improve the sinusoidal characteristics of the static air gap flux density waveform.And the suitable bow height is determined. Finally， a prototype is made based on the suitable bow height for experiments， and compared with the analytical result and the FE result， and the accuracy and effectiveness of the bow-shaped PMs with the suitable bow height are verified.

1. Introduction

The Control Moment Gyro(CMG)is an important part of the inertial actuator. Its main principle is to change the direction of angular momentum to adjust the attitude of the spacecraft.Due to the presence of magnetic bearings， the Magnetically Suspended Control Moment Gyro (MSCMG) has an air gap between the stator and the rotor， which eliminates the friction loss problem of the traditional mechanical gyro. It has the characteristics of non-lubricated， high speed， long life， high precision， continuous output of high torque and so on. It is gradually replacing mechanical control moment gyros and used on satellites.As an important part of MSCMG，the drive motor provides the required angular momentum. The drive motor for space needs to meet the performance requirements of low power consumption，high reliability，and long life.Currently， hollow-cup Permanent Magnet (PM) motors are used as drive motors on inertial actuators. The structure of hollow-cup PM motor is characterized by the use of the cupshaped stator without iron core， PMs on the outer rotor，and simultaneous rotation of inner and outer rotors. That overcomes iron loss and cogging torque ripple caused by iron core to achieve low power consumption and improve motor performance greatly， so it has a wide range of applications.Hollow-cup motors， as innovative products of motor technology in recent decades， have brought much concern from market and been widely used in military， aerospace， medical equipment， robotics， automotive industry and other fields.PM motor with sinusoidal air gap magnetic flux density waveform has advantages of low noise，fast starting speed and high operating efficiency. At present， tile-shaped PMs are mostly used in hollow-cup motors. Hollow-cup motors mostly use tile-shaped PMs， and the generated air gap flux density waveform has poor sinusoidal characteristics. The waveform contains a large number of harmonic components that cause the motor to generate torque ripple，which reduces the smoothness of the motor operation and affects the accuracy of the output.

For the purpose of making sinusoidal characteristic of air gap magnetic flux density waveform closer to the ideal sinusoidal wave， structural design and optimization are the main methods. Wang et al. used variable separation method to solve Maxwell equations， took different boundary conditions into consideration to construct air gap magnetic density mathematical model of Halbach array PMs， and reduce harmonic content by changing the height or width of PMs， making air gap magnetic flux density close to sinusoidal waveform. Zhou et al. constructed a surface-mounted motor air gap flux density distribution model through equivalent surface current method. On the basis of traditional tileshaped PMs， the air gap magnetic flux waveform density was close to a sinusoidal wave by decentering the outer arc. However， only the PMs were attached to the inner rotor for motor eccentricity，and the PMs attached to the outer rotor were not considered.Ren et al. proposed a PM installed on the outer surface of rotor， with a magnetically penetrating metal block in the surface of PM. They covered it with a magnetically permeable metal block of approximately sine shape to realize the unevenness of the air gap of the motor and finally optimized it.Kang et al.presented a design method to reduce cogging torque of interior-type PM motor. In this design method， optimal notches were put on the rotor pole face，which affected variation of PM shape or residual flux density of PM. Through the space harmonic field analysis， positions of notches were found， and optimal shapes of notches were determined by using FE method. A method to add auxiliary grooves in the rotor surface was proposed to optimize air gap magnetic field of Permanent Magnet Synchronous Motor(PMSM) and reduce iron loss， torque ripple and noise vibration caused by the harmonics. Minimization of vibration and noise was realized by forming optimal notches corresponding to the shape of the magnetic field on the rotor pole face. PM poles of surface-mount PMSM were designed to be sine or inverse cosine，that is，sine poles or inverse cosine poles，so that radial air gap flux density waveform of the motor was close to sinusoidal wave. However， only the case with a stator core was considered， and the influence of no stator core was not considered.. Koo et al.used a chamfering method for PMs to produce uneven air gap and reduce eddy current loss. The above methods are suitable for PM motors with stator cores， small air gaps， and PMs on inner rotor， while they are not applicable to a hollow-cup motor such as a PM motor without a stator core，a large air gap，and PMs on the outside.

This paper proposes a bow-shaped PMs structure that is designed for the hollow-cup motor. First， the model is analyzed by an equivalent surface current method. Then， the FE method is used to calculate the air gap flux density of conventional tile-shaped PMs and bow-shaped PMs with different bow heights. And the suitable bow height is determined.Finally，a prototype is made for experiments，the experimental results are compared with the analytical result and the FE result， and the accuracy and effectiveness of the bow-shaped PMs with the suitable bow height are verified.

2. Hollow-cup motor based on bow-shaped PMs modeling

Top view and cross-sectional view of the hollow-cup motor based on bow-shaped PMs are shown in Figs. 1 (a) and (b).Main structural components include outer rotor core， inner rotor core，PMs and cup-shaped stator.And PMs are attached to the outer rotor.

Based on the theory of electromagnetic field，combined with the boundary conditions in the air gap of the motor，and using the method of separating variables， the magnetic field generated by the bow-shaped PMs can be equivalent to the superposition calculation of several pairs of current-carrying coils.The magnetic field distribution generated by a pair of currentcarrying coils is shown in Fig. 2.

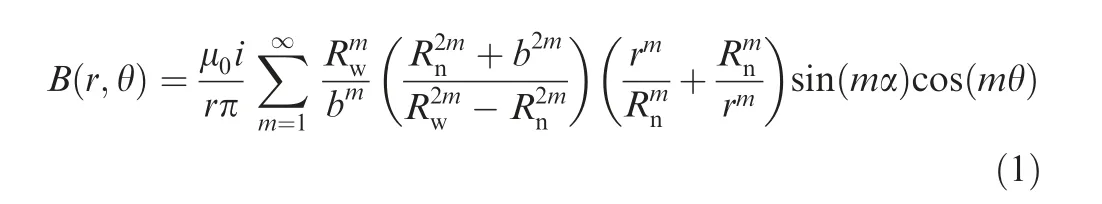
where Ris the inner radius of the outer rotor;Ris the outer radius of the inner rotor; the position of the pair of currentcarrying coil element sides A and B in the air gap where they are located in cylindrical coordinates is r ＝b ， θ ＝±α ; μis the relative permeability in the air; i is the equivalent surface radial current.

Considering that PM with parallel magnetization is more common， it is more practical to analyze air gap magnetic flux density generated by the parallel magnetized PM.During parallel magnetization， magnetization direction is parallel to the center line of bow-shaped PMs. According to equivalent surface current method， the equivalent surface current of the PMs is shown in Fig. 3. The surface current directions along PM surface AB and CD are opposite， but values are equal，which is

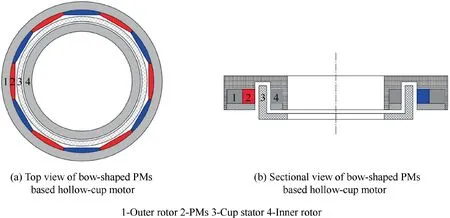
Fig. 1 Hollow-cup motor model based on bow-shaped PMs.

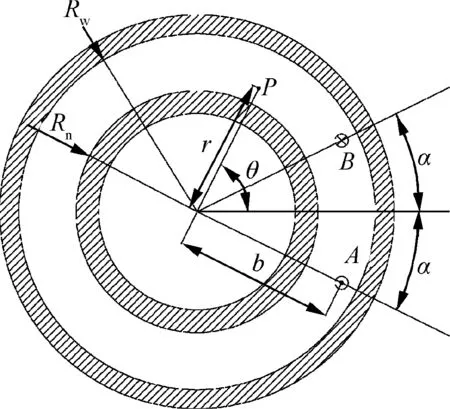
Fig. 2 A pair of current-carrying coils in motor air gap.

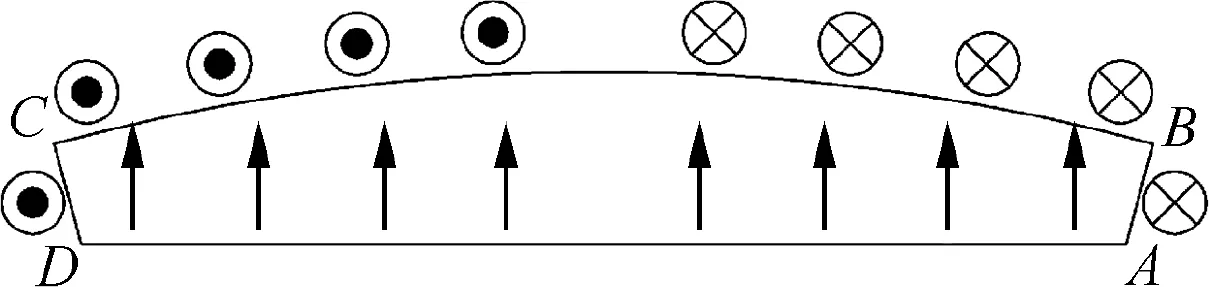
Fig. 3 Equivalent surface current of parallel magnetized bowshaped PM.

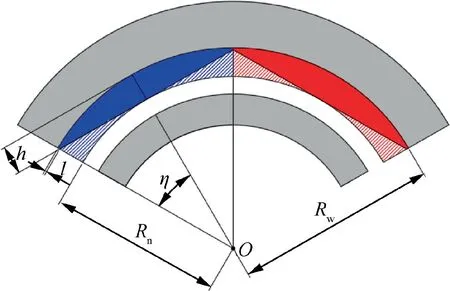
Fig. 4 Schematic diagram of bow-shaped PMs.

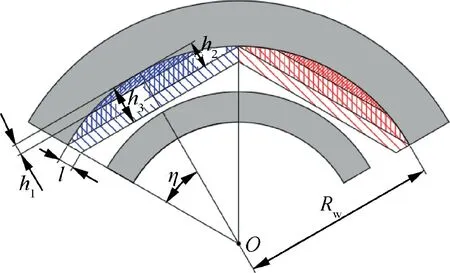
Fig. 5 Different bow heights of bow-shaped PMs.

Substitute Eq. (13) into Eq. (12)， and the air gap magnetic field distribution can be based on bow-shaped PMs. It can be seen from Eq. (7) and Eq. (13) that the strength of the air gap magnetic flux density is only related to the bow height h of bow-shaped PMs.

3. FE simulation analysis

The parameters of the hollow-cup motor based on bow-shaped PMs FE simulation model are shown in Table 1. The static magnetic density diagram of the FE simulation model is shown in Fig. 6.

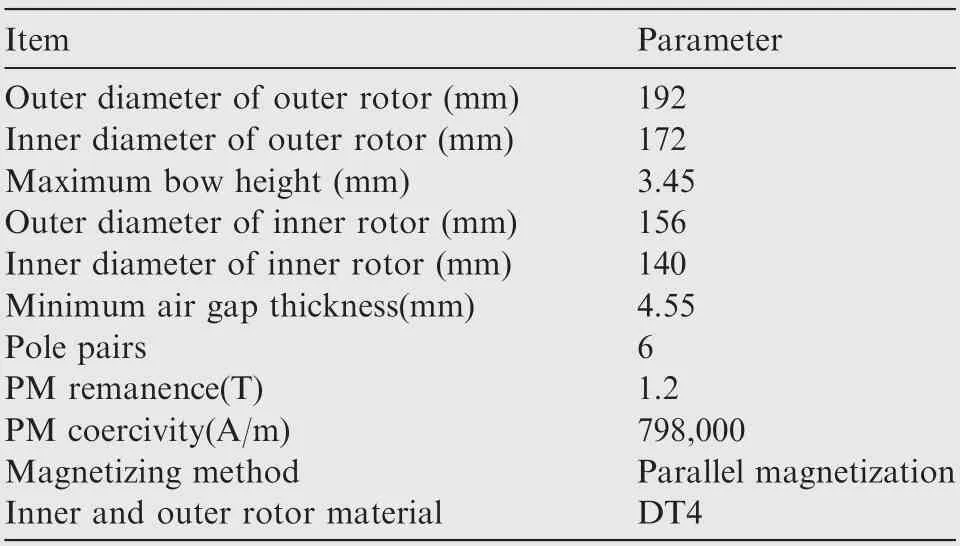
Table 1 Parameters of hollow-cup motor based on bowshaped PMs.

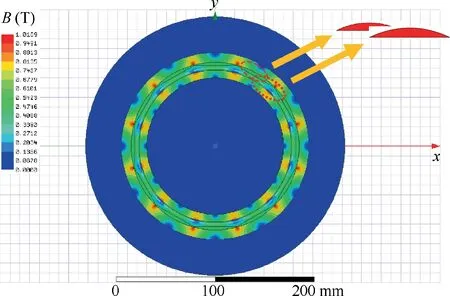
Fig. 6 FE simulation of bow-shaped PMs based hollow-cup motor.

For sinusoidal waveform， the evaluation index is mainly THD with calculation formula as follows:

where Gis the amplitude of the corresponding nth order harmonic， and its value is obtained by Fourier decomposition of the air gap magnetic flux density waveform.

The static air gap flux density waveform of bow-shaped PMs with different bow heights are analyzed and the corresponding THD is calculated. The curve of peak value and THD with bow height are shown in Figs. 7 (a) and (b). The bow height ranges from 2 to 3.5， and the interval is 0.25 mm.

The peak value of static air gap magnetic flux density increases with the increase of the bow height， and the THD value first decreases and then increases with the increase of the bow height.The minimum value of THD is selected under the premise that the difference between the static air gap magnetic density peak value and the static magnetic density peak value of the tile-shaped PMs (the static magnetic density peak value of the tile-shaped PMs in this paper is 0.45 T) is not large. Combining the two factors of THD and static air gap magnetic density peak value， we can see that the suitable bow height is 3.25 mm.

After FE simulation， suitable bow height PMs of the static air gap magnetic density waveform and the harmonic components of the waveform are obtained， and the obtained results are compared with the analytical results， as shown in Figs. 8(a) and (b).

Peak values in the static air gap magnetic flux density waveform of two results are very close.The THD value of the analytical result is 6.98% and the THD value of the FE result is 6.15%. The main reason for this difference is the idealization of the motor model and ignorance of factors such as local magnetic saturation and magnetic leakage.

The tile-shaped PMs based hollow-cup motor is simulated using the FE method. PMs adopt a tile-shaped PM with a thickness of 3.45 mm，and other parameters are consistent with Table 1. The FE model is shown in Fig. 9. The air gap magnetic density waveform and the harmonic components of the waveform are obtained as shown in Fig.10(a)and Fig.10(b).

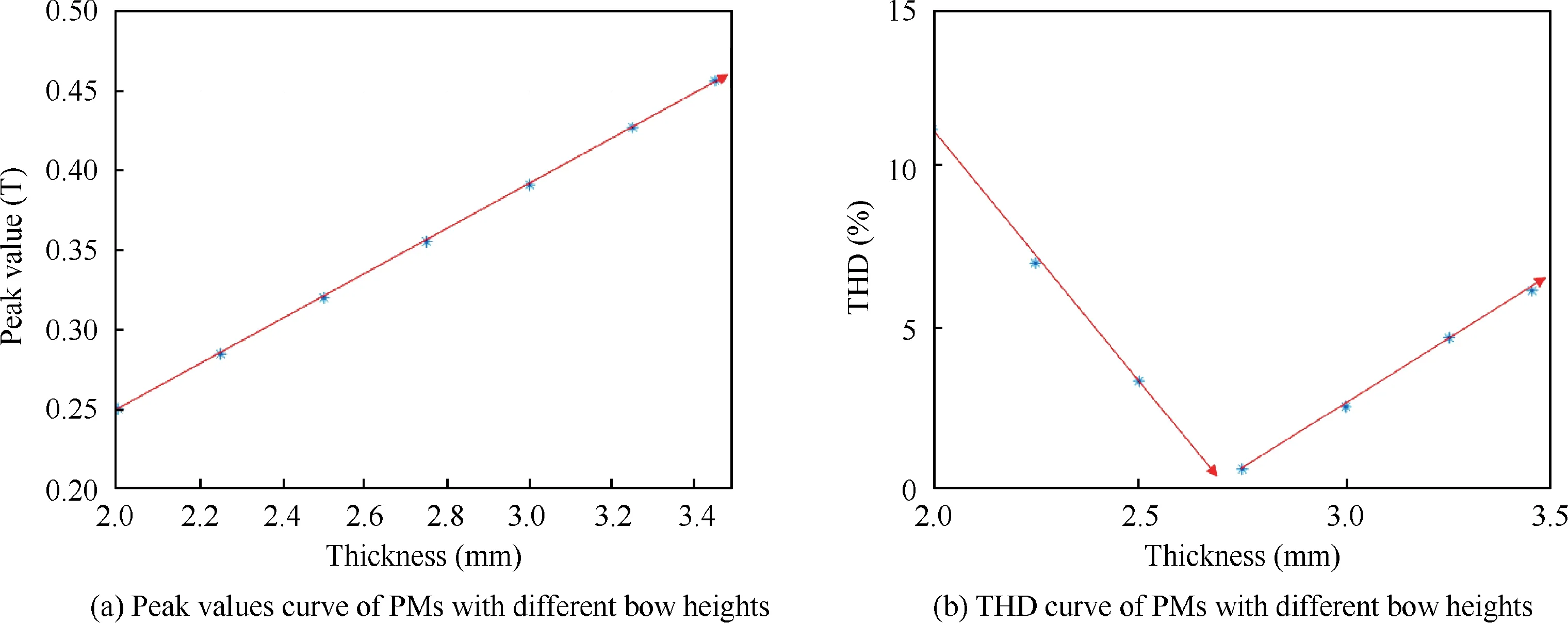
Fig. 7 Evaluation index of static air gap magnetic density with different bow heights.

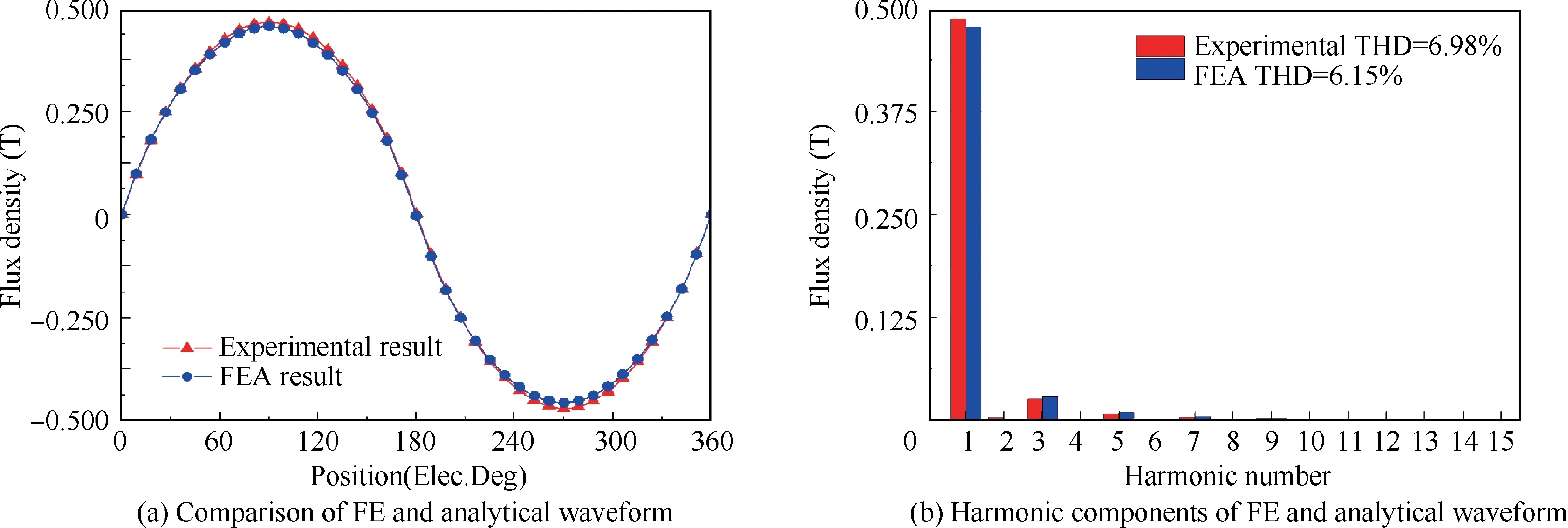
Fig. 8 Comparison of FE and analytical results.

Fig. 9 FE simulation of tile-shaped PMs based hollow-cup motor.

The FE results of the bow-shaped PMs and the tileshaped PMs are compared. The air gap magnetic density waveform generated by the bow-shaped PMs is close to a sinusoidal curve. The THD value of the bow-shaped PMs waveform is 6.15%， and compared with the THD value of the tile-shaped PMs waveform that is 29.25%， the THD value of the bow-shaped PMs air gap magnetic density waveform is significantly reduced. It also shows that the bow-shaped PMs improve the sinusoidal characteristic of the static air gap magnetic density.

4. Experimental verification

Experimental prototype design is shown in Fig. 11. It is composed of 4 parts: clamp， outer iron core， inner iron core， and PMs. The function of the clamp is to fix inner iron core and outer iron core so that the relative position of the two remains unchanged. Bow-shaped PMs are tightly attached to the inner side of the outer iron core.

Experimental platform before the experiment is shown in Fig.12(a).It is mainly composed of five parts:clamping mechanism， rotating platform， magnetometer， control panel and mechanical arm. The experimental platform is shown in Fig. 12(b). Firstly， experimental prototype is placed on the clamping mechanism and clamped. Secondly， the action of the mechanical arm is controlled by adjusting control panel，so that mechanical arm could drive magnetometer to reach the position of air gap and keep it still.Then，the experimental program is started， the experimental prototype is rotated by the rotating platform，and the program stops after the magnetometer collects the magnetic flux density of one round of the air gap. Finally， the experimental data are exported and processed.

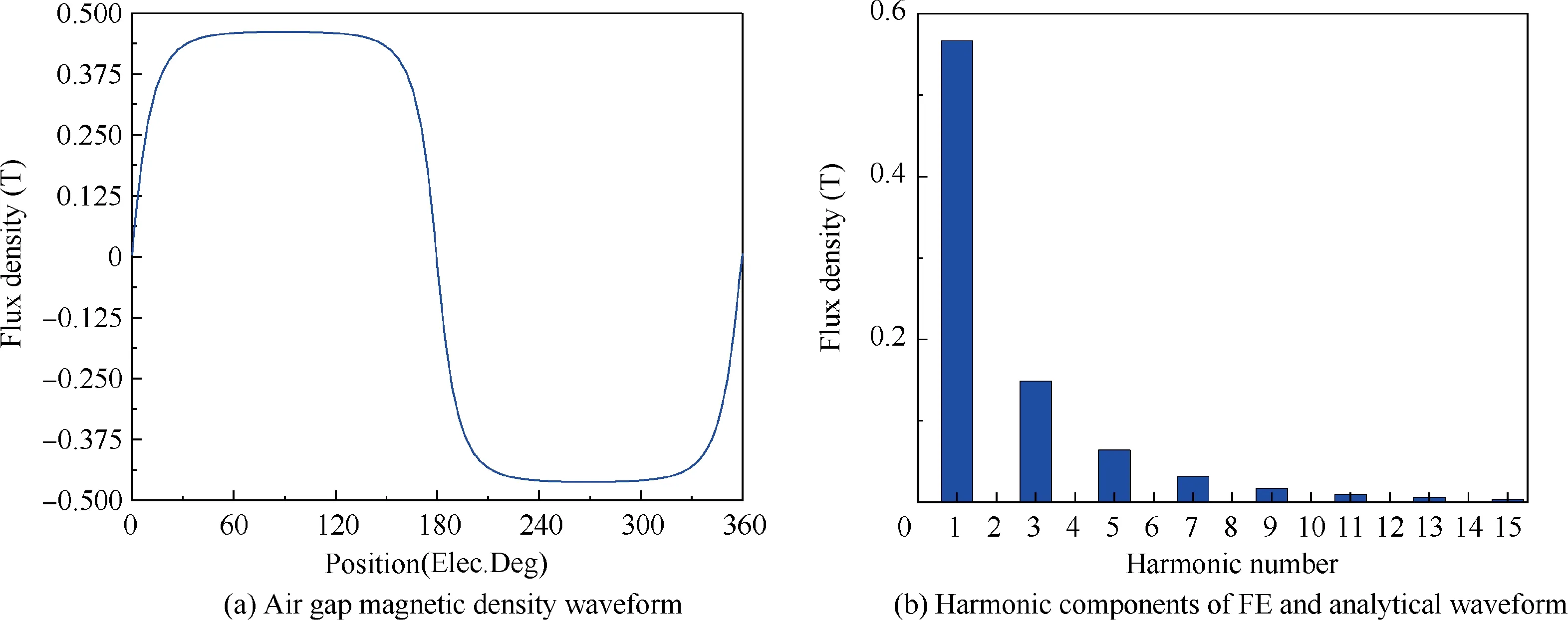
Fig. 10 FE simulation results of tile-shaped PMs based hollow-cup motor.

Fig. 11 Experimental prototype of bow-shaped PMs.

Fig. 12 Air gap magnetic flux density experimental platform.

After the experiment， the results of the air gap magnetic flux density waveform of the bow-shaped PMs and the harmonic components of the magnetic field waveform are compared. The comparison is shown in Figs. 13 (a) and (b). The experimental results of the hollow-cup motor model based on the bow-shaped PMs analyzed in this paper are consistent with the FE results. The reason for the differences in the analytical results is given in Section 3. The THD value of the FE result is 6.15%， and the THD value of the experimental result is 5.87%. There is little difference between the two， which verifies the correctness of the FE simulation， and shows that the hollow-cup motor model based on the bowshaped PMs can well improve the sinusoidal characteristics of the static air gap flux density waveform. Due to the fact that the thickness of the two ends of the bow-shaped PMs is relatively small， the bow-shaped PMs are fragile， which makes it difficult to process the bow-shaped PMs and the processing cycle is long.

Fig. 13 Comparison of analytical， FEA and experimental results.

5. Conclusions

In this paper，the equivalent surface current method is used to calculate the static air gap flux density analytic formula of the hollow-cup motor model based on bow-shaped PMs.Then，FE method is used to calculate the static air gap flux density waveform of conventional tile-shaped PMs and bow-shaped PMs with different bow heights. And the suitable bow height is determined. The FE results show that the THD value of the bow-shaped PMs with the suitable bow height is reduced by 78.97% compared with that of the tile-shaped PMs. It is concluded that the bow-shaped PMs structure can improve the sinusoidal characteristics of the static air gap flux density.The experimental prototype is made for experimental verification， and the analytical result， FE result and experimental result are compared and analyzed. Owing to ignoring factors such as local magnetic saturation and magnetic flux leakage，the difference between the analytical result and the FE result of the THD value is 0.83%. The experimental result and the FE result are in good agreement， and the difference between the two is 0.28%. The bow-shaped PMs can effectively improve the sinusoidal characteristics of the hollow-cup motor static air gap flux density waveform.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This study was supported by the National Natural Science Foundation of China (Nos. 52075017，62073010) and the Excellent Youth Science Foundation of China(No.51722501).