An effective crack position diagnosis method for the hollow shaft rotor system based on the convolutional neural network and deep metric learning

Yuhong JIN， Lei HOU，*， Yushu CHEN， Zhenyong LU

a School of Astronautics， Harbin Institute of Technology， Harbin 150001， China

b Institute of Dynamics and Control Science， Shandong Normal University， Ji’nan 250014， China

KEYWORDS Convolutional neural networks;Cracked rotor;Deep metric learning;Fault diagnosis;Hollow shaft rotor

Abstract In recent years，the crack fault is one of the most common faults in the rotor system and it is still a challenge for crack position diagnosis in the hollow shaft rotor system. In this paper， a method based on the Convolutional Neural Network and deep metric learning (CNN-C) is proposed to effectively identify the crack position for a hollow shaft rotor system.Center-loss function is used to enhance the performance of neural network. Main contributions include: Firstly， the dynamic response of the dual-disks hollow shaft rotor system is obtained.The analysis results show that the crack will cause super-harmonic resonance，and the peak value of it is closely related to the position and depth of the crack. In addition， the amplitude near the non-resonant region also has relationship with the crack parameters.Secondly，we proposed an effective crack position diagnosis method which has the highest 99.04%recognition accuracy compared with other algorithms.Then，the influence of penalty factor on CNN-C performance is analyzed，which shows that too high penalty factor will lead to the decline of the neural network performance. Finally， the feature vectors are visualized via t-distributed Stochastic Neighbor Embedding (t-SNE). Naive Bayes classifier(NB) and K-Nearest Neighbor algorithm (KNN) are used to verify the validity of the feature vectors extracted by CNN-C.The results show that NB and KNN have more regular decision boundaries and higher recognition accuracy on the feature vectors data set extracted by CNN-C，indicating that the feature vectors extracted by CNN-C have great intra-class compactness and inter-class separability.

1. Introduction

Rotating machinery plays an important part in modern industry dynamic systems， such as gas turbines， aero-engine and wind turbines， and the health of rotating machinery is very important to the stable operation of machinery equipment.However，due to harsh working environment and the overload operations， the crack fault in the rotor system often appends，which can pose a serious threat to the reliability of rotating machinery operating. Therefore， in order to make timely and accurate fault diagnosis for the crack fault of the rotor system，many researches have studied this problem in many areas.In the aspect of crack model， Gasch first proposed a hingespring model that can characterize the effect of cracks.Then，Mayesand Al-Shudeifatet al. proposed a cosine breathing function and a new type of breathing function by using the Fourier series， to more accurately represent the crack breathing process， respectively. The comparative results show that the respiration function based on the Fourier series is more accurate but its form is complex. Furthermore， in terms of the dynamic response characteristics of the cracked rotor system and fault diagnosis， Jun et al.deduced the equation of motion for a simple rotor with a breathing crack. It is found that the second harmonic components near to 1/2 first-order critical speed is the vibration characteristics related to the crack in the rotor system.Chasalevris and Papadopoulosanalyzed the coupling problem of longitudinal vibration and flexural vibration of the rotor system with two transverse breathing cracks， and the phenomenon of the critical speed changes with the crack depth was observed. Guo et al.adopted a crack fault diagnosis method based on the Empirical Pattern Decomposition (EMD) of a simple Jeffcott rotor， and the experimental verification were carried out. Lu et al.studied the vibration response of a hollow shaft dual-rotor system with breathing crack. The relationship between the peak value of the super-harmonic resonance and the dimensionless depth of the crack was discussed. Hou et al.found the super-harmonic resonance phenomenon of the cracked rotor due to maneuver load， and analyzed its bifurcation characteristics. Then， Gao et al.studied the dynamic behavior of a flexible asymmetric rotor system under the maneuvering flight，which considered rolling bearing and Squeeze Film Dampers(SFDs) nonlinearity. Zeng et al.established the Finite Element Model (FEM) for a compressor blade with an open crack， which introduced the typical fatigue cracks analyzed in referenced crack propagation path simulation and experimental tests. Fu et al.investigated the dynamic behaviors of a hollow-shaft rotor system with an open crack under inherent model uncertainties by using the Uncertain Response Surrogate Function (URSF)， and results show that the surrogate function has good accuracy and robustness. These studies mainly focus on the dynamic response characteristics of the cracked rotor system or qualitative analysis of the crack parameters influence， such as the relationship between the super-harmonic resonance peak and the depth or position of the crack. However， in many cases， crack fault diagnosis requires quantitative relationships between the dynamic response characteristics and the crack parameters.

In recent years，Machine Learning and Deep Learning techniques have acquired great success in in many fields such as computer vision， fault diagnosis and pattern recognition.Many researchers also use these methods to study the fault diagnosis of the rotor system.Janessens et al.presented a feature learning model for rotating machinery condition monitoring based on the Convolutional Neural Network (CNN). By taking the Discrete Fourier Transform (DFT) of normalized vibration signal collected by two accelerators as input， the CNN can output four classification categories representing bearing health conditions， including healthy bearing， mildly inadequately lubricated bearing， extremely inadequately lubricated bearing，and outer raceway fault.In Ref.20，Zhang et al.proposed a new CNN structure， which was denoted as TICNN. In TICNN， kernel size of the first convolution layer is set to a large value， such as 256 × 1， and the testing results showed that the TICNN model can achieve pretty high accuracy under noisy environment. Besides， in view of the existing problems of traditional fault diagnosis methods，Zhang et al.designed a preprocess method which could convert the original vibration signals into 2D images， and combined this method with CNN. Based on this preprocessing method， 2D format CNN model can process time series data in 1D format directly.Subsequently， different from the study adopting the CNN or other deep learning models alone， Ma and Chuproposed a diagnosis method for rotor and bearing faults of rotating machinery based on ensemble learning. By integrating the sub-learners including Convolution Residual Network(CRN)，Deep Belief Network(DBN)，and Deep Auto Encoder(DAE)， integrated learning method achieves high accuracy on the multi-fault classification problem. Li et al.proposed a new network called adaptive 1D separable convolution with residual connection. Compared to the traditional 1D CNN，the proposed method can effectively reduce the complexity of the network while achieving a great identification accuracy.Zhang et al.made use of the fuzzy neural network for the rotary machines fault diagnosis， and experimental results verified that this method has great identification ability. In addition， aim at the small sample problem， Wang et al.developed a new fault diagnosis model adopting the Weighted Extension Neural Network (W-ENN). Compared with vanilla Extension Neural Network (ENN)， better fault diagnosis results are obtained for turbo-generator sets. Most of these recent studies are based on the actual vibration signals measured from the rotating machinery. But in Ref. 26， Li et al.conducted a disparate study by utilizing the CNN model and Infrared Thermography (IRT). Infrared thermal images of the rotating machinery are captured by the IRT technique，then，a CNN model is applied for the fault mode identification.The comparison results show that the performance of CNN is better than DBN and DAE.However，Ref.27 pointed out that the domain shift problem is a huge challenge of pattern learning validity in Deep Learning techniques.Due to environment noise and variation of working situation， domain shift phenomenon may have a serious impact on the performance of neural network. Therefore， in order to address domain shift problem， researchers proposed Metric Learning and Deep Metric Learning methods. Metric Learning is a new method to solve the pattern recognition problems such as fault diagnosis and face recognition.It aims to learn a distance function on a specific task，which can help improve the performance of traditional machine learning classification algorithms. Deep metric Learning is a method of metric learning.Its goal is to learn a mapping from the original input data to the low-latitude dense vector space (called the embedding space)， which can make the distance between the similar objects in the embedding space using common distance functions smaller (that is，to enhance the intra-class compactness)， while the distance between the objects of different classes is relatively large (that is， to improve the inter-class separability). In the field of rotor system fault diagnosis， Deep Metric Learning has also been used by researchers. Wang and Liuproposed Triplet Loss guided Adversarial Domain Adaptation method (TLADA)for bearing fault diagnosis.This method achieved good results in CWRU dataset and Paderborn dataset. Yang et al.proposed an intelligent fault diagnosis approach based on Feature-based Transfer Neural Network (FTNN) from laboratory bearings to locomotive bearings. The regularization terms of multi-layer domain adaptation and pseudo label learning are developed to impose constraints on the parameters of the CNN so as to reduce the distribution discrepancy and the among-class distance of the learned transferable features. Li et al.introduced a robust intelligent fault diagnosis method for rolling element bearings based on deep metric learning， which is effective for environmental noise and unknown working conditions. Yu et al.employed a threestage Semi-Supervised Learning (SSL) approach to increase the identification performance of the classifiers using Data Augmentation (DA) and metric learning. Li et al.adopted the auto-encoder structure， distance metric learning and kmeans clustering method to address the data sparsity issue with insufficient labeled data. Xie et al.proposed a crossdomain feature extraction method of the time and frequencydomain based on the Transfer Component Analysis (TCA)for the gearbox fault diagnosis with various operating conditions.Zhang et al.employed a fault diagnosis method based on the convolutional neural network which is proposed for the weak vibration signal of the casing under the excitation of rolling bearing fault. The experiment results show that the fault characteristics of rolling bearing are more easily expressed by continuous wavelet scale spectrum， and a better recognition rate is obtained.However，most of these researches are mainly focus on making fault classification for the rotary machinery，and there are relatively little researches on crack position diagnosis of hollow shaft rotor systems based on Deep Learning and Deep Metric Learning.

In this study， a new crack position diagnosis method for a two-disks hollow shaft rotor system based on the convolutional neural network and deep metric leaning is proposed.At present， the research object of most researchers about the rotor system crack fault diagnosis is the solid shaft rotor or Jeffcott rotor. Nevertheless， in practical problems， most large complex rotor systems adopt the hollow shaft， which can improve the rotor operating efficiency. The dynamic response of the rotor system is simultaneously affected by the depth and position of the crack， so it is still a challenge to identify the crack position when the depth of the crack is unknown.In this paper， the dynamic response of a cracked dual-disks hollow shaft rotor is studied， and the convolutional neural network with center-loss (CNN-C) is estimated to solve the crack position diagnosis problem. The results show that the proposed method has the highest test accuracy compared with other machine learning algorithms.Besides，the feature vectors visualization results via t-SNE indicate that the feature vectors extracted by the proposed method have better intra-class compactness and inter-class separability. Naive Bayes classifier(NB)and K-Nearest Neighbor algorithm(KNN)achieve great recognition accuracy in the data set reconstructed by the convolution and pooling operations of CNN-C， which indicate that CNN-C can be adopted as an effective feature extraction algorithm for the crack position diagnosis.

2. Dynamic response analysis of a dual-disks hollow shaft rotor with a breathing crack

2.1. The motion equation of the crack rotor system

The finite element model of the cracked double-disks hollow shaft rotor system is shown in Fig. 1， which is divided into 20 elements and 21 nodes. Each end of the rotor (node 1 and node 21) has a bearing and support. There are 2 disks in this rotor system，which respectively locate at node 5 and node 17.The shaft of this model is hollow，which has inner radius r and outer radius R. Moreover， to better fit the actual failure status， the crack may locate in any element of the shaft. The physical parameters of the model are shown in Table 1.

For the hollow shaft section，the crack has two forms:nonpenetrating crack and passthrough crack， as shown in Fig. 2.

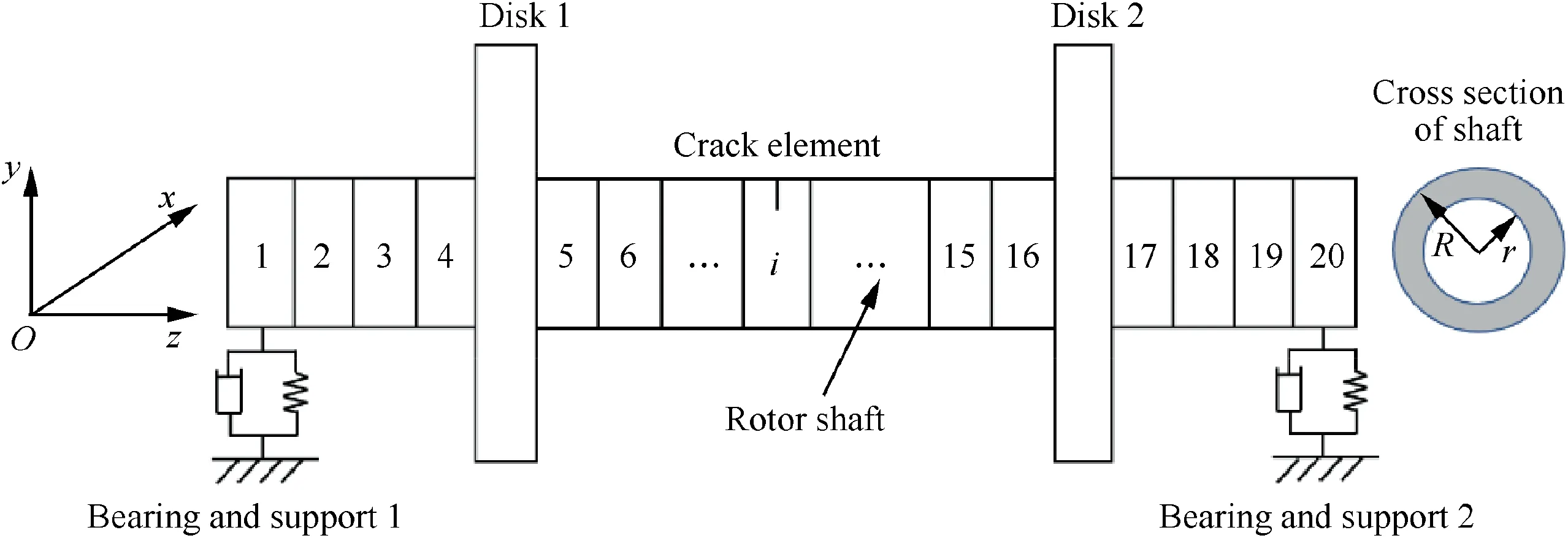
Fig. 1 Finite element model of a dual-disks hollow shaft rotor with a breathing crack.

Table 1 Physical parameters of rotor system.

Aand Arepresent the cross-sectional area of uncracked and cracked segments respectively.O-xy is the fixed coordinate system and C－xy－ is the centroid coordinate system， where C is the centroid of the section A. h and e represent crack depth and centroid offset distance. α and αare the angles between the crack edge and O. And in this paper， the breathing function of the crack is given as

2.2. Equation solving

In this paper，the Harmonic Balance Method(HBM)is considered to solve Eq.(2)，which supposes that the stable solution of the equation has the finite Fourier series solution as shown in Eq. (3)

By substituting Eq.(4)and Eq.(5)into Eq.(3)，the steadystate dynamic response of the hollow shaft rotor system with a crack can be obtained.

2.3. Dynamic response analysis

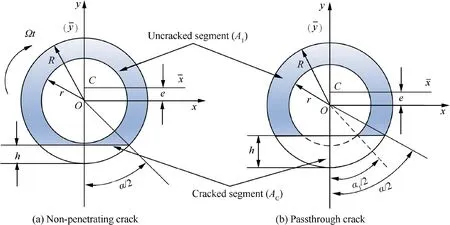
Fig. 2 Different forms of hollow shaft crack.

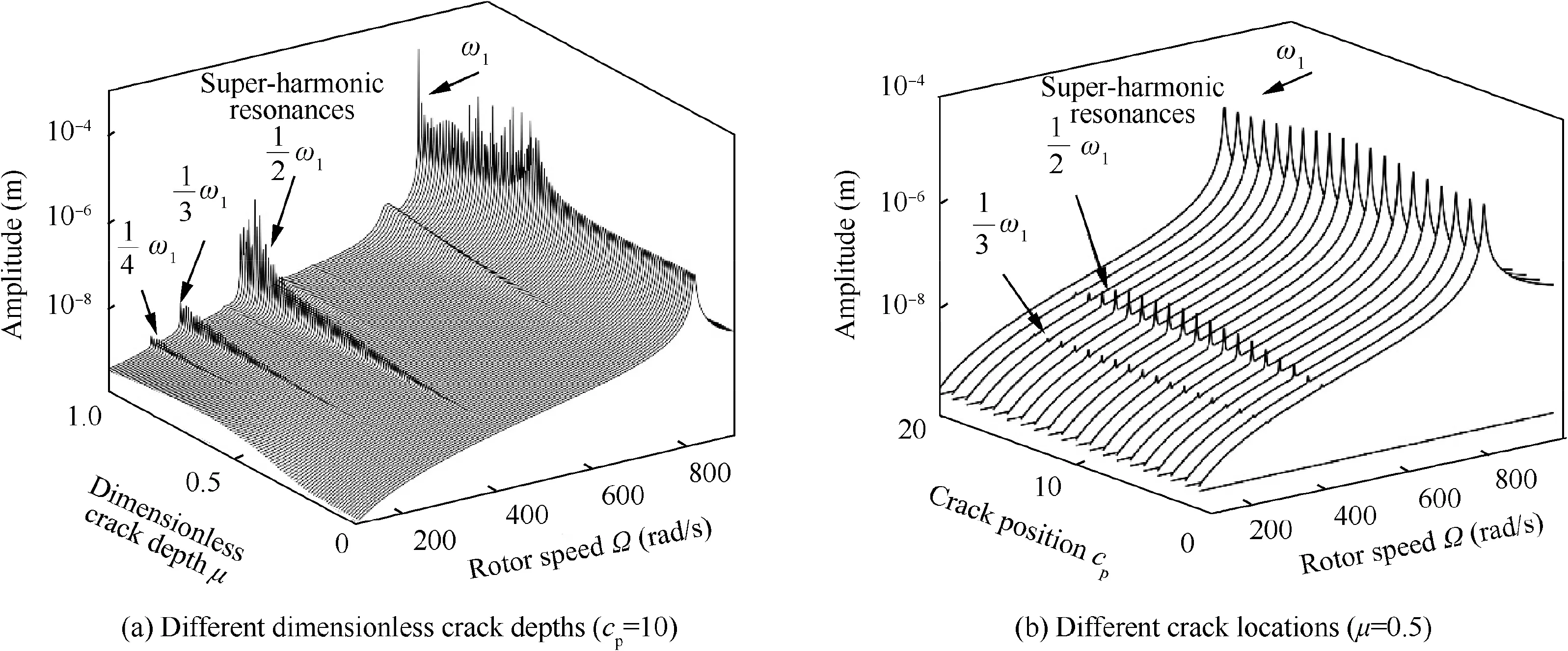
Fig. 3 3D waterfall diagrams of the crack rotor system.

To analyze the Dynamic response of the crack rotor system，Fig. 3(a) shows the 3D waterfall diagram of rotor speeddimensionless crack depth-amplitude at node 10 near the first critical speed ωand the position of the crack c= 10. From the analysis of Fig. 3(a)， it can be seen that the generation of the crack has a significant impact on the dynamic response of the rotor system. First of all， the crack causes the superharmonic resonance of the rotor system near the 1/2， 1/3 and 1/4 critical speed， and this phenomenon becomes more and more obvious with the increase of the crack depth. Then， the depth of the crack can impact the vibration amplitude of the rotor system in the super-harmonic resonance region and the non-resonance region. The generation of the crack can be approximately equivalent to weakening the stiffness of the rotor shaft， so the amplitude of the rotor system will increase slightly， and with the increase of the crack depth， the amplitude of the rotor system also shows a trend of gradual increase.

In addition，to analyze the effect of crack position，Fig.3(b)calculates the 3D waterfall diagram of rotor speed -crack position-amplitude at node 10 and the dimensionless depth of the crack μ is fixed at 0.5.It can be seen from Fig.3(b)that the dynamic response of the rotor system is also related to the location of the crack. When the crack is close to both ends of the rotor system，the influence of the crack is very weak due to the existence of supports， that is， the super-harmonic resonance peak in the amplitude-frequency curve of the rotor system is not obvious. However， under the same crack depth，when the crack is located in the middle of the shaft， the dynamic response of the rotor system will be more affected，and the super-harmonic resonance phenomenon of the rotor system is more obvious.

3. Crack position diagnosis method based on the convolutional neural network and deep metric learning

In this section， in order to effectively diagnose the crack position of the rotor system， a crack position fault diagnosis method based on the convolutional neural network (CNN)and deep metric learning is proposed.

3.1. The convolutional neural network

The convolutional neural network (CNN) is a deep learning network structure that can effectively process sequence type data such as pictures and time series. Because of their strong feature extraction ability， CNN has been widely applied in a lot of fields such as fault diagnosis and computer vision in recent years. Classical convolutional neural network architecture mainly includes convolutional layer， pooling layer， batch normalization layer， activation function and Softmax classifier.

It can be seen from Eq.(7)that the dimension of the feature sequence after the operation of the convolutional layer is N+k－1，which is attenuated compared with the dimension N of the original input sequence.In order to eliminate the limitation of dimension attenuation on the depth of the convolutional neural network， the padding method is commonly used to improve Eq. (7)， as shown in Eq. (8)

Of course， there are many strategies to pad， and Eq. (8)only gives a more commonly used form. In CNNs， there are usually multiple convolutional layers. In order to distinguish，the output of the jth convolutional layer is denoted as y.

A pooling layer is generally added after the convolutional layer in convolutional neural networks. The function of the pooling layer is to down-sample the output of the convolutional layer，increase the receptive field of neurons，and reduce the dimension of features to avoid the‘‘dimension curse”.The pooling functions in the pooling layer include average-pooling，max-pooling， etc. The most commonly used pooling function in pattern recognition problems is the max-pooling function，and its formula is described as follows

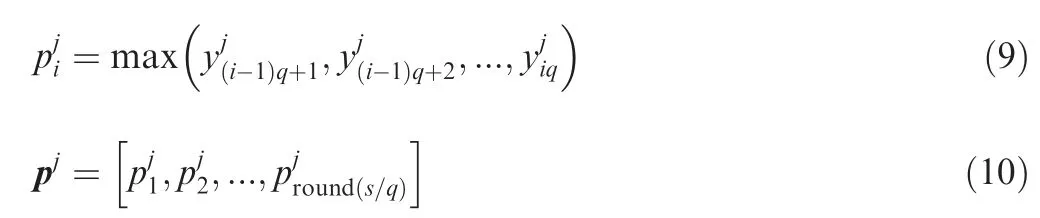
pis the output of the jth pooling layer， and its dimension is round (s/q)， where s is the input dimension of the pooling layer， q is the kernel size of the pooling layer， and round (*)represents the ceiling function. A complete CNN usually contains multiple pooling layers and convolutional layers for feature extraction， and then a fully connected layer and Softmax classifier are added to the top of the network to make classification. Softmax classifier can output the discrete probability density of each category. Assuming that the number of classification categories is k， the estimated probabilities of the input data belonging to each category can be obtained by Eq. (11).

3.2. Deep metric learning

Deep metric learning is an important research direction in current deep learning research. The main research purpose is to enhance the performance of neural networks by designing new network structure or improving the loss function for the pattern recognition problems.The results in Ref.36 show that the use of deep metric learning method to learn embedding space from the available data can achieve better results in many pattern recognition problems.

The loss function commonly used in the traditional CNNs for the pattern recognition problems is the cross-entropy loss function， which is denoted as Land the formula of it is defined as

where m is the number of samples， χ denotes the indicative function. Softmax classifier combined with cross-entropy loss function has achieved great results in many pattern recognition problems.However，in some cases，we care more about the feature vectors xin the embedding space obtained by the original data after multiple convolution and pooling operations in the CNNs than the final recognition accuracy. If the feature vectors xhave great intra-class compactness and inter-class separability，then the multiple convolution and pooling operations can be used as an effective feature extraction algorithm for this pattern recognition problem.After employing this feature extraction algorithm to reconstruct the data set， a relatively simple machine learning method such as K-Nearest Neighbor classification algorithm(KNN)can also achieve better results. However， related studies have shown that if only the Softmax classifier combined with the cross-entropy loss function is adopted to train the CNNs， the feature vectors xdo not necessarily have clustering characteristics. On the contrary， xwill try to fill the entire embedding space. Therefore， it is necessary to use some metric learning methods to improve it.

The advanced loss functions commonly used in the deep metric learning include triplet loss， center-loss and so on. In this paper， the center loss function is adopted to enhance the loss function in the training of the CNNs.The center-loss function is defined as

3.3. Structure of the CNN with center-loss

From the analysis results in Section 2， it can be observed that the crack will cause super-harmonic resonance in the rotor system，and the peak value of super-harmonic resonance is closely related to the position and depth of the crack.In addition，the amplitude near the non-resonant region also has a certain relationship with the crack parameters. Then， in the actual engineering， the effective value is used to calculate the amplitude can avoid the influence of noise. Therefore， the amplitudefrequency response of the rotor system near low speed can be utilized as a basis for the crack position fault diagnosis.Therefore， the amplitude-frequency response of the cracked rotor system at speed range from 100 rad/s to 1000 rad/s is taken as the input sequence of the CNN. The output of the neural network is the probability of the crack belonging to each position category， where every two elements is taken as a class (denoted as C1， C2 to C10). Based on this input and output and referring to the AlexNet， structure of the CNN combined with the center-loss function (abbreviated as CNN-C) in deep metric learning adopted in this paper is shown in Fig. 4.

Since the input data is an amplitude-frequency response sequence of 1D， the convolution layer and the pooling layer also adopt 1D.All convolutional layers take the leaky rectified linear unit (Leaky ReLU) as the activation function. Compared with the traditional ReLU， an adjustable hyperparameter α is added to Leaky ReLU to give the activation function a smaller gradient in the negative region and avoiding the problem of‘‘dying ReLU”.In addition，to improve the stability of the features learned by the neural network， a Batch Normalization layer(Batch Norm)is added after the first convolutional layer. The input data is mapped to the new embedding space after three convolution and pooling operations.The feature vectors in the embedding space is connected to the Softmax classifier and the center-loss part according to Eq.(14)， then， the discrete probability value of each category can be obtained. The structural parameters of the proposed CNN-C model are shown in Table 2.

4. Results and discussion

4.1. Identification of crack position using the proposed CNN-C model

Random numbers are used to generate the dimensionless depth and position of the crack. According to the method in Section 2， the amplitude-frequency response data set of the cracked rotor system is constructed by simulation calculation.The data set contains 10，019 sets of amplitude-frequency responses of the rotor system with different crack depths and crack positions in the low speed range from 100 rad/s to 1000 rad/s. 70% of the data set is randomly selected as the training set for training the CNN-C proposed in this paper，and the remaining 30%is used as the testing set to test the performance of the neural network. The stochastic gradient des-cent method is used to train CNN-C， the training algorithm adopts the Nadam algorithm， the batch size of the training set is set to 4， and the maximum training epochs is 50. When the penalty factor λ of the central-loss function in Eq. (14) is 0.2， the training process of CNN-C is shown in Fig. 5.

Table 2 Structural parameters of the proposed CNN-C model.

It can be seen from Fig.5(a)that the loss function of CNNC on the training set and testing set shows a trend of oscillating attenuation as the training progresses. When the training stops， the loss function values of CNN-C on the training set and the testing set are respectively 0.09872 and 0.05736. Both of them are relatively small and not significantly different，indicating that the CNN-C does not have serious over-fitting phenomenon.Furthermore，Fig.5(b)shows the change process of recognition accuracy， and the analysis results denotes that the recognition accuracy of the CNN-C on the training set and testing set increases gradually with the training. When the training is terminated， the recognition accuracy of the CNNC on the training set is 97.79%， and the recognition accuracy on the testing set is 99.04%. The recognition accuracy of CNN-C on both the training set and testing set is high and their difference is not large， indicating that CNN-C has great performance.

Fig. 4 Structure of the proposed CNN-C model.

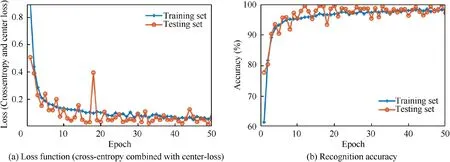
Fig. 5 Training process of CNN-C.

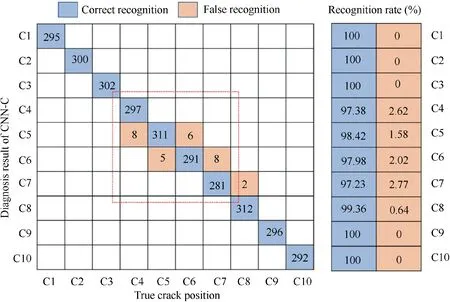
Fig. 6 Confusion matrix of CNN-C on the testing set.

Then， to analyze the influence of different crack positions on the diagnosis results， the confusion matrix of CNN-C on the testing set is shown in Fig. 6. It can be seen from the confusion matrix that the false identification results of CNN-C are mainly concentrated in C4，C5，C6 and C7，which indicate that CNN-C has a relatively high identification accuracy when the crack is located at both ends of the rotor system.Nevertheless，if the crack is located in the middle of the rotor system， the identification accuracy of CNN-C decreases slightly. This is because when the crack is located at both ends of the rotor system， the impact of the crack on the dynamic response of the rotor system is relatively weak due to the existence of supports，so the change of the crack depth will not cause great fluctuations in the super-harmonic resonance peak value. Therefore，CNN-C can obtain more accurate fault diagnosis results.However， when the crack is located at the middle of the rotor system， the crack will have a great influence on the dynamic response of the rotor system. The change of crack depth will make the peak value of super-harmonic resonance fluctuate greatly(see in Fig.3(a)).This phenomenon can make the rotor system produce similar dynamic responses at different crack locations，thus resulting in confusion of the CNN-C identification results.

Fig. 7 Comparison of fault diagnosis accuracy of different model.

Furthermore， in order to further verify the effectiveness of the CNN-C proposed in this paper for the fault diagnosis of the rotor system crack position，Fig.7 compares the fault diagnosis accuracy of CNN-C with other commonly used machine learning algorithms in the pattern recognition problems，including Naive Bayesian classifier (NB)， Random Forest(RF)， Multi-Layer Perceptron (MLP)， Support Vector Machine (SVM) and the traditional Convolutional Neural Network (CNN). The number of estimators of RF is 800 and the max leaf nodes is 16.The number of hidden layer neurons of MLP denotes 30.Then， the kernel function of SVM is radial basis function. Fig. 7 illustrates that the recognition accuracy of NB， RF and MLP on the testing set are 37.92%，69.93% and 75.68%， respectively. The accuracy of all three algorithms remains below 80%， which means that they perform poorly in crack position diagnosis. In contrast， SVM is much more precise than NB，RF and MLP，achieving 87.79%accuracy on the testing set，but the performance of SVM is still not valid enough.Besides，the accuracy of CNN on the testing set is improved to 97.07%， indicating that CNN is more suitable for the crack position fault diagnosis in the rotor system.Compared with CNN， the proposed CNN-C model in this paper has the highest recognition accuracy of 99.0% on the testing set， which is 1.97% higher than CNN. This raise of accuracy means that CNN-C reduces the misclassification by nearly 70%compared to CNN.The results of Fig.7 show that the center-loss function can effectively improve the performance of CNN， which verify the effectiveness of the proposed CNN-C model in the crack position fault diagnosis for the rotor system.

4.2. The impact of the penalty factor λ

In this section，we will discuss the influence of the penalty factor λ in Eq.(14).Fig.8(a)shows the changes in the accuracy of CNN-C on the training set and testing set under different penalty factors. As can be seen from Fig. 8(a)， when the penalty factor λ is 0， that is， center-loss is not considered in the loss function at all， CNN-C is equivalent to CNN， and the recognition accuracy on the training set and testing set is 95.96%and 97.07%， respectively. While when λ is 0.2， the loss function of CNN-C contains both cross-entropy and center-loss.At this time， the accuracy of CNN-C on the training set and testing set reaches 97.85% and 99.04%， which is a certain improvement compared with λ = 0. However， as shown in Eq.(13)，the definition of the center-loss function cannot make classification. The effect of center-loss is only to enhance the intra-class compactness of the feature vectors in the embedding space. Therefore， the performance of CNN-C and λ is not a simple positive correlation. If λ is too large， CNN-C will mainly tend to reduce center-loss with ignoring the crossentropy in the training process，that is，it will compress the feature vectors of all samples to a certain point in the embedding space while neglecting the inter-class separability， which leads to the degradation of the neural network performance. The analysis results in Fig. 8(a) also proves this conclusion. The accuracy of CNN-C with λ =0.4 on the training set and testing set is 93.18% and 95.48%， respectively. The performance of CNN-C has declined. If λ is further increased to 0.6，CNN-C remains 89.19% accuracy on the training set and 89.85% accuracy on the testing set. Compared with CNN-C with λ = 0.2 and CNN， its performance is significantly reduced. In addition， Fig. 8(a) also illustrates the calculation results in the extreme case when λ=∞. In this case， only the part of center-loss is considered， and the testing set accuracy of CNN-C is 10.05%， which is worse than random guessing. The above results indicate that CNN-C can achieve the best performance only if an appropriate penalty factor is set.

Fig. 8(b) presents the variation curve of the intra-class distance of samples in the embedding space of CNN-C under different penalty factors during the training process， where the distance function is Euclidean distance. It can be seen that when λ = 0， that is， when the center-loss is not considered，as the training progresses， the intra-class distance of the training samples shows a trend of gradual increase in a small range.At the end of training， the intra-class distance is 5.95 × 10.The large intra-class distance means that the intra-class compactness of the feature vectors in the embedding space is poor，which is a typical problem of Softmax classifier and crossentropy.Terrible intra-class compactness will limit the generalization ability of the neural network，and if the original data is mapped，but the intra-class compactness of the feature vectors in the embedding space is not great， it means that the performance of this mapping is not good， so we need to use center-loss to improve it. As shown by the blue line in Fig. 8(b)， when λ = 0.2， the variation trend of intra-class distance turns from increasing to decreasing compared with the training process without center-loss，indicating that the intra-class compactness of the feature vectors is gradually improving. At the end of the training， the intra-class distance is 0.161， which is much smaller than the result without center-loss， and the intra-class compactness of samples is greatly improved. Further increasing the penalty factor λ， it can be found that the intra-class distance under λ = 0.4 and λ = 0.6 at the end of training is 0.131 and 0.101， respectively， indicating that the intra-class distance of samples decreases with the increase of λ. These conclusions are similar to the results in Ref. 36.

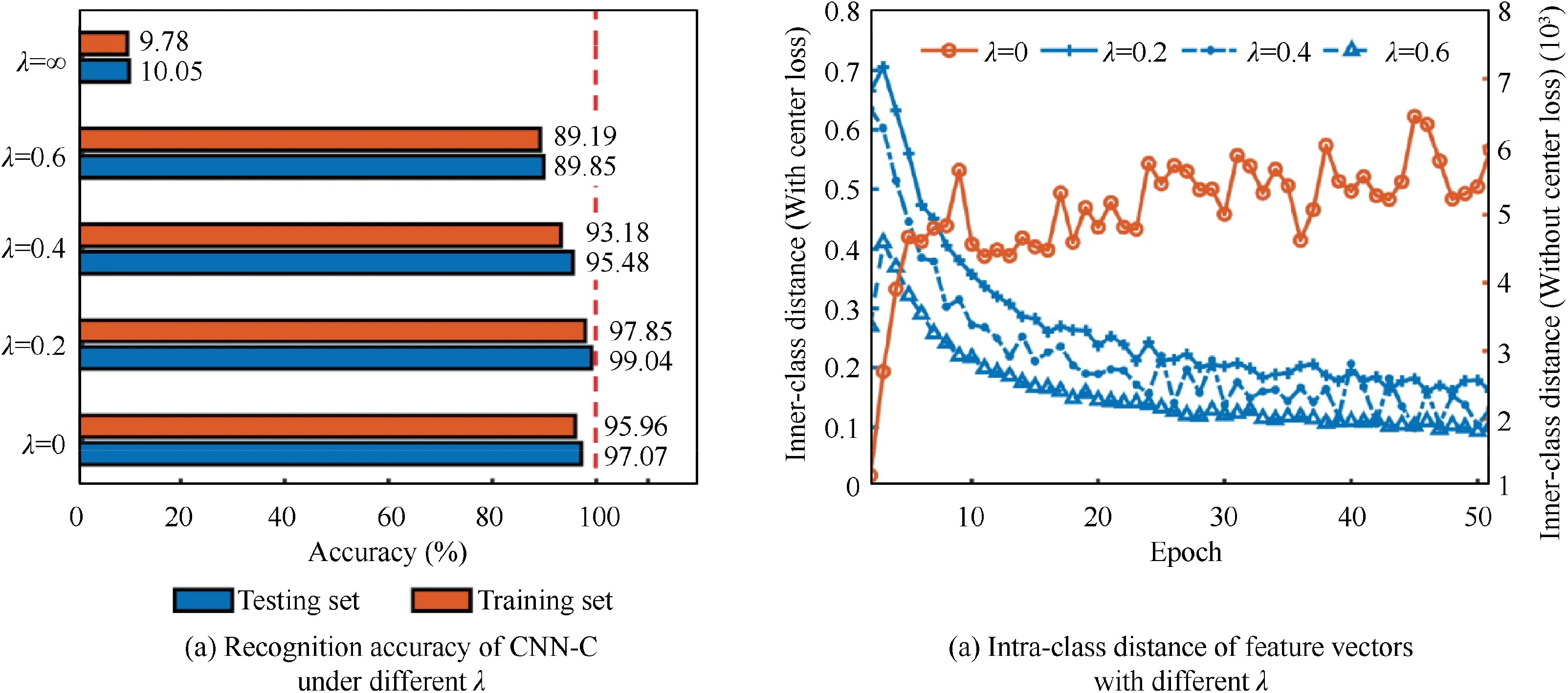
Fig. 8 Impact of the penalty factor λ.

4.3. Feature vectors visualization

In pattern recognition problems such as fault diagnosis，for the proposed classifier model， compared to the final recognition accuracy， the distribution of the sample feature vectors in the embedding space is sometimes more meaningful.If the distribution of the feature vectors has great intra-class compactness and inter-class separability， then this model can be adopted as an effective feature extraction method. So， in this section，we focus on discussing the feature extraction effectiveness of CNN-C for the crack position fault diagnosis.

First， to better observe the distribution of feature vectors calculated by the proposed crack position fault diagnosis method based on CNN-C， it is necessary to visualize the feature vectors in the embedding space. However， after multiple convolution and pooling operations of the input data， the dimension of the feature vectors obtained is 50. The embedding space is a high-dimensional vector space that cannot be directly visualized. Therefore， dimensionality reduction processing of the feature vector is required. Widely adopted data dimensionality reduction and visualization methods mainly include Principal Component Analysis (PCA)， t-distributed Stochastic Neighbor Embedding (t-SNE)， etc. Among them，t-SNE solves the problems of crowded sample distribution and unobvious boundaries after dimensionality reduction in other methods， which is recognized as a better dimensionality reduction and visualization method at present. Fig. 9 and Fig. 10 show the feature vectors visualization results on the testing set of CNN and CNN-C via t-SNE during training process. In the initial of training， the feature vectors between different categories have large overlap parts， and the distinction between classes is not strong (as shown in Figs. 9(a)， 9(b)， 10(a) and 10(b))， which is the reason why the recognition accuracy of CNN-C and CNN in the early stage of training is not high.As the training progresses，the feature vectors of different categories are gradually separated， and the inter-class separability is enhanced (as shown in Figs. 9(c)， 9(d)， 10(c)and 10(d))， so the recognition accuracy of CNN and CNN-C will gradually increase.At the end of training，the feature vector distributions of the testing set of CNN and CNN-C are shown in Fig.9(e)and Fig.10(e).The comparison results show that although both of them show a certain degree of inter-class separability， there is still large overlapping parts between the different class feature vectors in CNN， as shown by the circle in Fig.9(e)，and the distribution form of the same class feature vectors is a long strip， indicating that the feature vectors extracted by CNN will tend to fill the entire embedding space，and does not have good intra-class compactness.Therefore，in the crack position fault diagnosis of the rotor system，the convolution and pooling part of the trained CNN model cannot be regarded as an effective feature extraction method. In contrast， there is almost no obvious overlap between the feature vectors of different categories in Fig. 10(e)， illustrating that the feature vectors extracted by CNN-C have better interclass separability. And it can also be seen from Fig. 10(e) that the distribution shape of the same class feature vectors obtained by CNN-C is cluster， showing great clustering characteristics， indicating that the intra-class compactness of feature vectors is also better. The feature vectors extracted from the convolution and pooling parts of CNN-C have both good inter-class separability and intra-class compactness， so the operation of this part can be adopted as an effective feature extraction method in the crack position fault diagnosis of the rotor system.

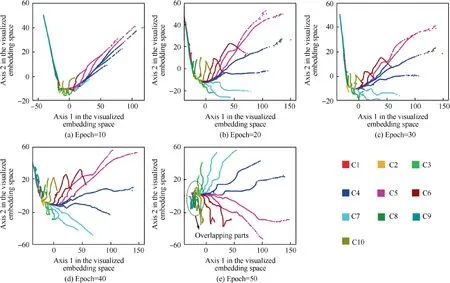
Fig. 9 Feature vectors visualization via t-SNE of CNN.

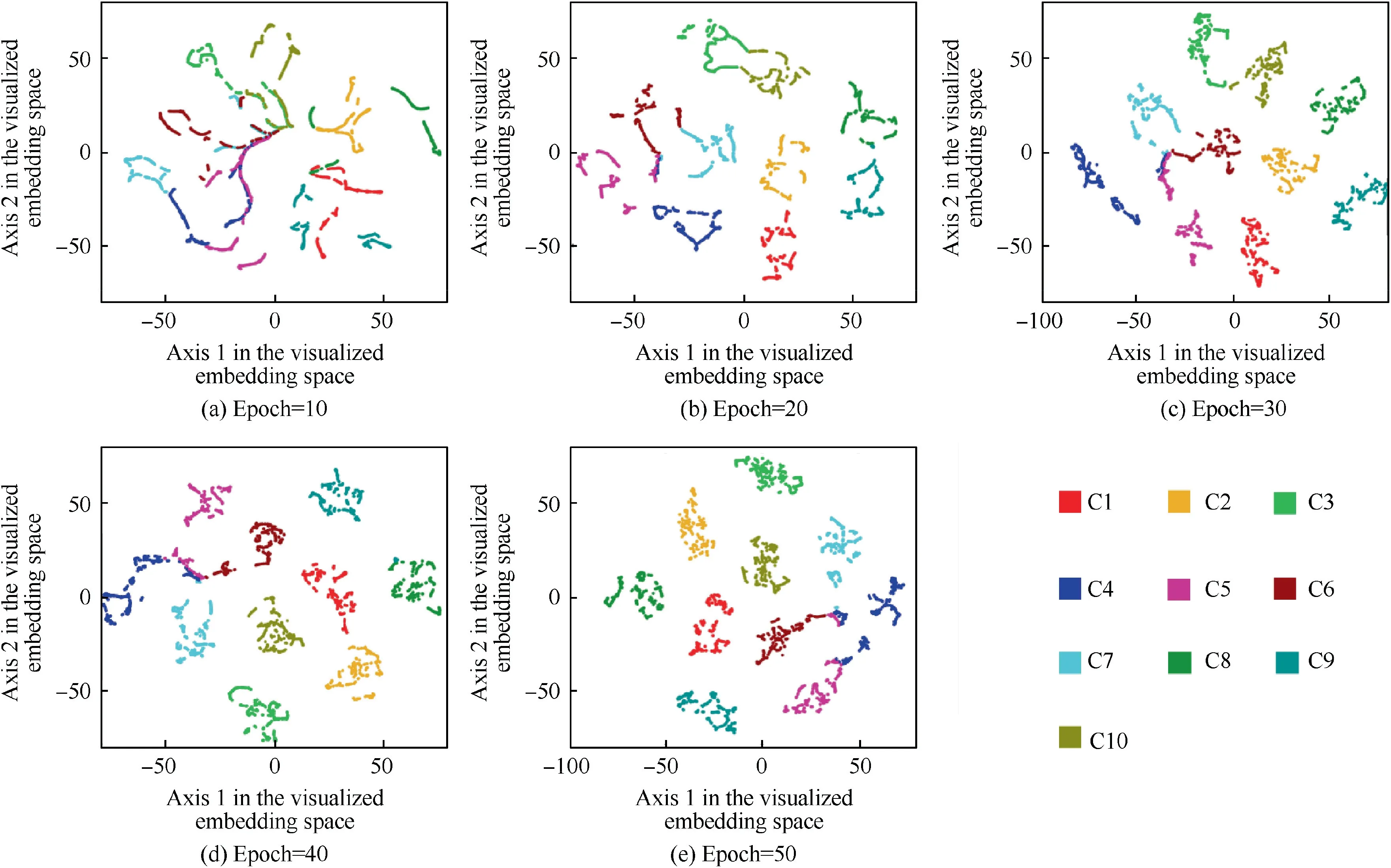
Fig. 10 Feature vectors visualization via t-SNE of CNN-C.

In order to further explain the advantages of CNN-C in feature extraction compared with CNN， the convolution and pooling parts of CNN-C and CNN are used as feature extraction algorithms，and t-SNE dimension reduction technology is adopted to reconstruct the original 1 × 901 data set into 2D data set(denoted as DataSet1 and DataSet2 respectively).Subsequently， NB and the k-nearest neighbor algorithm (KNN)are selected to train and test on the reconstructed 2D data set. If the feature extraction method is effective， the recognition accuracy of NB and KNN should also be great. Fig. 11 and Fig. 12 show the decision boundaries of NB and KNN on DataSet1 and DataSet2， separately. We can observe that NB has obvious irregular decision boundaries on Dataset1 due to the poor intra-class compactness and inter-class separability of feature vectors in Dataset1 (see in Fig. 11(a)). This irregular decision boundaries generally mean that NB has serious overfitting on DataSet1，and it cannot achieve good recognition results. Besides， the final recognition accuracy also illustrates this conclusion. The accuracy of NB on the testing set of Dataset1 is only 63.77%， which is better than 38.26%on the original data set (see in Fig. 6)， but its performance is still poor. Therefore， the convolution and pooling parts of CNN are not an effective feature extraction algorithm for the rotor system crack position diagnosis problem.In contrast，from the calculation results in Fig. 11(b)， it can be seen that since the feature vectors in Dataset2 have good intra-class compactness and inter-class separability， the recognition results of NB on Dataset2 is significantly improved compared with that in Fig. 11(a). The region formed by the decision boundaries are block-shaped，and there are no obvious irregular decision boundaries. Besides， the testing recognition accuracy on DataSet2 of NB also reaches 98.15%， which is 34.38%higher than DataSet1 and 59.89%higher than original data set. KNN also has similar results. As shown in Fig. 12，KNN has irregular decision boundaries on DataSet1， the recognition accuracy is 75.81%， and the effect is poor. However， there are no obvious irregular decision boundaries on DataSet2，and the accuracy is 92.38%，which is 16.56%higher than DataSet1， and a better fault diagnosis result is achieved.Besides，there is an interesting result that the accuracy of KNN is higher than NB on DataSet1 but lower on DataSet2. NB and KNN have achieved great recognition results in DataSet2，with regular decision boundaries and high recognition accuracy， indicating that the convolution and pooling part of CNN-C can be used in the crack position fault diagnosis of the rotor system as a more effective feature extraction algorithm.

Fig. 11 Decision boundaries of NB on DataSet1 and DataSet2.

Fig. 12 Decision boundaries of KNN on DataSet1 and DataSet2.

5. Conclusions

In this paper， a dual-disks hollow shaft rotor system model with a breathing crack has been established based on the finite element method and the dynamic response of the cracked rotor system has been obtained by 4th HBM.Then，a crack location diagnosis method based on the convolutional neural network and deep metric learning has been proposed.Finally，the effectiveness of the proposed method has been verified，meanwhile，the feature vectors visualization has been presented. The main conclusions are as follows.

(1) The generation of the crack leads to the super-harmonic resonance phenomenon in the rotor system，and the peak values of the super-harmonic resonance is closely related to the depth and location of the crack.Besides，the crack has a certain influence on the amplitude of the rotor subsystem at non-resonant speed， and these dynamic response characteristics can be used as an effective basis for the crack fault diagnosis of the rotor system.

(2) Based on the convolutional neural network (CNN) and center-loss function， the crack position identification method CNN-C is proposed. CNN-C can achieve 99.04%accuracy inthe testing set containing3006 samples.The confusion matrix of CNN-C on the testing set show that the identification accuracy of CNN-C will decrease slightly if the crack is located in the middle of the rotor system. Then， compared with traditional machine learning methods，such as NB，RF，MLP，SVM and CNN，CNNChasthehighestrecognitionaccuracy，whichindicatesthat the advanced crack position fault diagnosis method based on CNN-C is more effective.

(3) The penalty factor λ will affect the performance of CNN-C，and since the center-loss function cannot make classification， the penalty factor is not as high as possible.When λ is too large，the performance of CNN-C will decline. From the perspective of the intra-class distance change of the feature vectors in the embedding space during training process， adding center-loss to the loss function can effectively improve the intra-class compactness of the feature vectors.

(4) t-SNE dimensionality reduction and visualization method is used to analyze the feature vectors distribution of CNN and CNN-C in the embedding space. It is found the intra-class compactness and inter-class differentiation of the feature vectors extracted by CNN-C are obviously better than that of CNN method. The recognition accuracy of NB and KNN in Dataset2(CNN-C) is 98.15% and 92.38%， which is about 34.38% and 16.56% higher than that in Dataset1(CNN). It indicates that the convolution and pooling parts of the fault diagnosis method of rotor system crack location based on CNN-C proposed in this paper can be used as an effective feature extraction algorithm.

In future work，more attention should be paid to experimental verification.It is necessary to verify the effectiveness of the proposed method in noise environment based on the measured data.Moreover，by adjusting hyperparameters (such as kernel size，stride，number of layers，etc.)or adopting some advanced neural network architecture (such as attentional mechanism，residual module，batch convolution module，etc.)，it is also possible to tune the performance of the proposed model.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

It is very grateful for the financial supports from the National Natural Science Foundation of China(No.11972129)and the National Major Science and Technology Projects of China(No. 2017-IV-0008-0045).