A homogenization-planning-tracking method to solve cooperative autonomous motion control for heterogeneous carrier dispatch systems

Jie LIU， Xinzhou DONG， Xinwei WANG， Kiki CUI， Xiwng QIE，Jun JIA

a War Research Institute， Academy of Military Sciences， Beijing 100850， China

b Department of Engineering Mechanics，State Key Laboratory of Structural Analysis for Industrial Equipment，Dalian University of Technology， Dalian 116024， China

c Naval Aeronautical University， Yantai 264000， China

d Baimtec Materials Co.， Ltd， Beijing 100094， China

KEYWORDS Autonomous motion control;Carrier dispatch system;Heterogeneous system;Cooperative trajectory planning;Receding horizon control;Weight optimization

Abstract Taxiing aircraft and towed aircraft with drawbar are two typical dispatch modes on the flight deck of aircraft carriers. In this paper， a novel hierarchical solution strategy， named as the Homogenization-Planning-Tracking(HPT)method，to solve cooperative autonomous motion control for heterogeneous carrier dispatch systems is developed. In the homogenization layer， any towed aircraft system involved in the sortie task is abstracted into a virtual taxiing aircraft. This layer transforms the heterogeneous systems into a homogeneous configuration. Then in the planning layer，a centralized optimal control problem is formulated for the homogeneous system.Compared with conducting the path planning directly with the original heterogeneous system， the homogenization layer contributes to reduce the dimension and nonlinearity of the formulated optimal control problem in the planning layer and consequently improves the robustness and efficiency of the solution process.Finally， in the tracking layer， a receding horizon controller is developed to track the reference trajectory obtained in the planning layer.To improve the tracking performance，multi-objective optimization techniques are implemented offline in advance to determine optimal weight parameters used in the tracking layer. Simulations demonstrate that smooth and collision-free cooperative trajectory can be generated efficiently in the planning phase. And robust trajectory tracking can be realized in the presence of external disturbances in the tracking phase.The developed HPT method provides a promising solution to the autonomous deck dispatch for unmanned carrier aircraft in the future.

1. Introduction

Carrier aircraft are the main combat weapons on aircraft carrier，and the sortie efficiency and safety greatly affect the combat efficiency of the carrier. In traditional sortie tasks，commanders first make dispatch plan based on artificial expertise. During this phase， one must synthesize complex factors such as sortie priority， path coordination and resource occupancy，etc.This phase grows harder and becomes prone to fail as the number of aircraft increases.When the dispatch order is released， each aircraft involved in the task is then dispatched between certain positions， either driven by pilots or towed by traction systems. In this phase， the dispatch path is usually designed by the pilot/driver himself. However， the flight deck is a narrow space with many obstacles， including both static and moving ones. The complex operational environment，along with possible human factors such as visual obstruction and fatigue， contribute to the possibility of severe accident.

To improve efficiency and safety of the dispatch process，various Computer Aided Deck Operation Systems (CADOSs)have been developed.There is an emerging consensus that the path planning should be taken as a primary module in CADOSs.With help of such a module，safe and efficient coordinated dispatch paths without collisions can be generated automatically， and it can possibly provide time information(i.e.， the departure and the arrival time of each path) which is necessary input for the upper-level mission planning module to handle precedence constraints. Additionally， trajectory tracking techniques can be further integrated to realize a fully automatic driving on the flight deck， which will greatly reduce the operational burden for the pilot/driver during the actual dispatch.

There are typically three dispatch modes of carrier aircraft，i.e.， aircraft taxiing， towed aircraft with drawbar and towed aircraft without drawbar. The first two modes are typically used on the flight deck， while the latter one is mainly used in the hanger. Most dispatch path planning techniques focus on problems where only one aircraft/traction system is involved.A recent review papercategorizes related techniques into five kinds，i.e.，Dijkstra’s algorithms，improved A*algorithms，1behavior dynamics based algorithms，intelligent search methodsand optimal control based methods.The above five kinds of techniques can be further divided into two groups， i.e.， geometric methods (including the first three ones) and trajectory planning methods (including the last one)， according to whether the kinematics are considered. As for an intelligent search method， its classification depends on the detailed discretization method. Along with a series of way-points provided in geometric methods， extra time information corresponding to the way-points is also available in trajectory planning methods. However， geometric methods generally own better computational efficiency and robustness than trajectory planning methods.

When applying the above methods to fleet launching problems，it is not allowed for multiple aircraft to be dispatched on deck simultaneously， without making full use of the space on the flight deck. To improve the sortie efficiency for multiple aircraft， some efforts have been made to develop cooperative dispatch planning techniques recently. Related researches can be divided into the following two groups.

(1) In the first group， it is assumed that each aircraft has been allocated with a catapult in advance and the core work is to generate feasible cooperative paths. Liu et al.develop a compound path planning technique to solve cooperative trajectory for multiple aircraft taxiing on flight deck.This method divides the whole trajectory into two parts.In the first part，an improved Reciprocal Velocity Obstacle (RVO) method that integrates the Dubins curve and kinematics is applied to realize efficient collision avoidance. In the second part， as an aircraft approaches around the terminal desired position，the symplectic pseudospectral method， which is an efficient optimal control method， is applied to meet the high requirement of terminal orientation. Wang et al.propose a centralized optimal control method that integrates the Progressively Constrained Strategy (PCS).The PCS used in Ref. 17 divides the optimization problem into three stages， where the taxiing kinematics，a part of constraints on state and control variables，and collision-free conditions are addressed successively.Such a warm-starting approach great facilitate the convergence. In Refs. 16，17， the number of aircraft involved is equal to the number of catapults.On the basis of Ref.8，Wu et al.consider a more realistic scenario where the number of aircraft involved is larger than the number of catapults in. In Ref. 19 a distributed path planning method based on the asynchronous planning strategy is proposed to address the deadlock phenomenon. In Ref. 20， trajectory tracking techniques are further integrated to smoothen the generated path. The above two methods are both classified into distributed path planning techniques， where avoidance of the dead-lock phenomenon needs further investigation.

(2) As in the second group， results on catapult allocation are considered unknown and need to be optimized as well as the dispatch path. In this group of methods， the taxiing time consumptions between each pair of catapult and aircraft are calculated in advance.Cui et al.decompose the overall problem into two consecutive optimization problems， where the catapult allocation and the launching sequence at each catapult are determined subsequently. Liu et al.formulate the problem as a flexible flowshop scheduling model，both catapult allocation and launching sequence are determined simultaneously by the genetic algorithm. The path coordination therein is achieved by introducing the priority principle. It perfectly eliminates deck-lock thus improving the robustness.Considering the limited number of traction systems， two different dispatch modes may be used simultaneously on deck， which leads to the path planning of heterogeneous systems.However，to the best of our knowledge，such a topic has not been studied so far.

Autonomous vehicles， including Unmanned Carrier Aircraft (UCA) and Unmanned Traction Systems (UTSs)， may be equipped on carriers in the near future due to the prosperity of artificial intelligence. UCA and UTSs must taxi/drive by themselves since there are no pilots/drivers.Hence，when feasible trajectories are generated， trajectory tracking techniques must be integrated to realize autonomous dispatch. To deal with trajectory tracking issues on flight deck，Model Predictive Control(MPC)techniques have been widely investigated in the recent five years.In MPC techniques， an open-loop optimal control is solved at each sampling instants. And the tracking control performance can be greatly affected by the following three aspects.The first one is the selection of control variables.In Ref. 6 oversimplified kinematics are used， and the taxiing velocity and front wheel steering angle are directly taken as the control variables， resulting in severe oscillations in such two control variables. The second one is the selection of weighted matrices. To the best knowledge of the authors，weighted matrices in existing related works are selected by trial and error. Actually， once a series of feasible trajectories are generated， weight optimization techniques can be integrated to achieve a better tracking performance， related work can be referred to Refs. 24，25. The third one is the computational efficiency of the core solver. Once the online computational efficiency is low， a relatively large sampling interval must be adopted， resulting in poor resistance to external disturbances.In addition， considering the aircraft won’t deviate much from the reference trajectory， the reference trajectory can be taken as the initial guess for each open-loop problem to speed up the convergent process.

In this paper， we focus on the cooperative autonomous motion control for heterogeneous carrier dispatch systems.Two typical dispatch modes on the flight deck，i.e.，taxiing aircraft and towed aircraft with drawbar， are considered. To address this issue， a novel hierarchical solution strategy，named as the Homogenization-Planning-Tracking (HPT)method， is developed. The HPT method first abstracts any towed aircraft system involved into a virtual taxiing aircraft，then the original trajectory planning problem for heterogeneous systems is transformed into one for homogeneous ones.Such a simplification can reduce the dimension and nonlinearity of solution. The centralized optimal control model is then established for cooperative trajectory planning of the homogeneous systems. The reference trajectory for these aircraft (including the virtual ones and the real ones) are obtained by pseudospectral methods.Finally， a trajectory tracking model is established to track the reference trajectory with the real kinematics. And the online optimal tracking algorithm based on Receding Horizon Control (RHC) is proposed，which can deal with the actual external disturbances. To further improve the tracking performance，a multi-objective optimization model is established， and NSGA-II is used to optimize the weight parameters in the tracking model offline in advance. The main contributions of the paper can be summarized as follows:

(1) Though we can formulate the centralized optimal control problem based on the original heterogeneous dispatch system， the large state space along with the high nonlinearity make it hard to be solved directly. To deal with this problem， the homogenization process is creatively introduced， thereby greatly improving the solution robustness and efficiency of the trajectory planning phase.

(2) Due to the benefit of the optimal control mathematical tools， various constraints on state and control variables can be strictly satisfied in the obtained reference trajectory.Moreover，it guarantees，theoretically，each aircraft can be dispatched exactly to the assigned destination with accurate terminal orientation. This is necessary for the aircraft to conduct subsequent operations.

(3) An RHC is designed to implement the tracking for reference trajectory. The NSGA-II method is applied to guide the selection of weighted coefficients in the RHC. A highly efficient computational optimal control method， i.e.， Symplectic Pseudospectral Method(SPM)，is taken as the core solver for the RHC，leading to an average computational time of 14 ms for each control instant. The RHC can well track the reference trajectory even in the presence of external disturbance.

The remainder of the paper is organized as follows. Section 2 first describes kinematics of two dispatch modes considered in the paper， and then formulates the cooperative trajectory planning problem of heterogeneous dispatch systems. In Section 3， we describe the HPT method and the multi-objective weight optimization process. Section 4 gives the numerical experiment and discussion. Finally， Section 5 concludes the paper.

2. Problem formulation

2.1. Kinematics

2.1.1. Towed aircraft system with drawbar

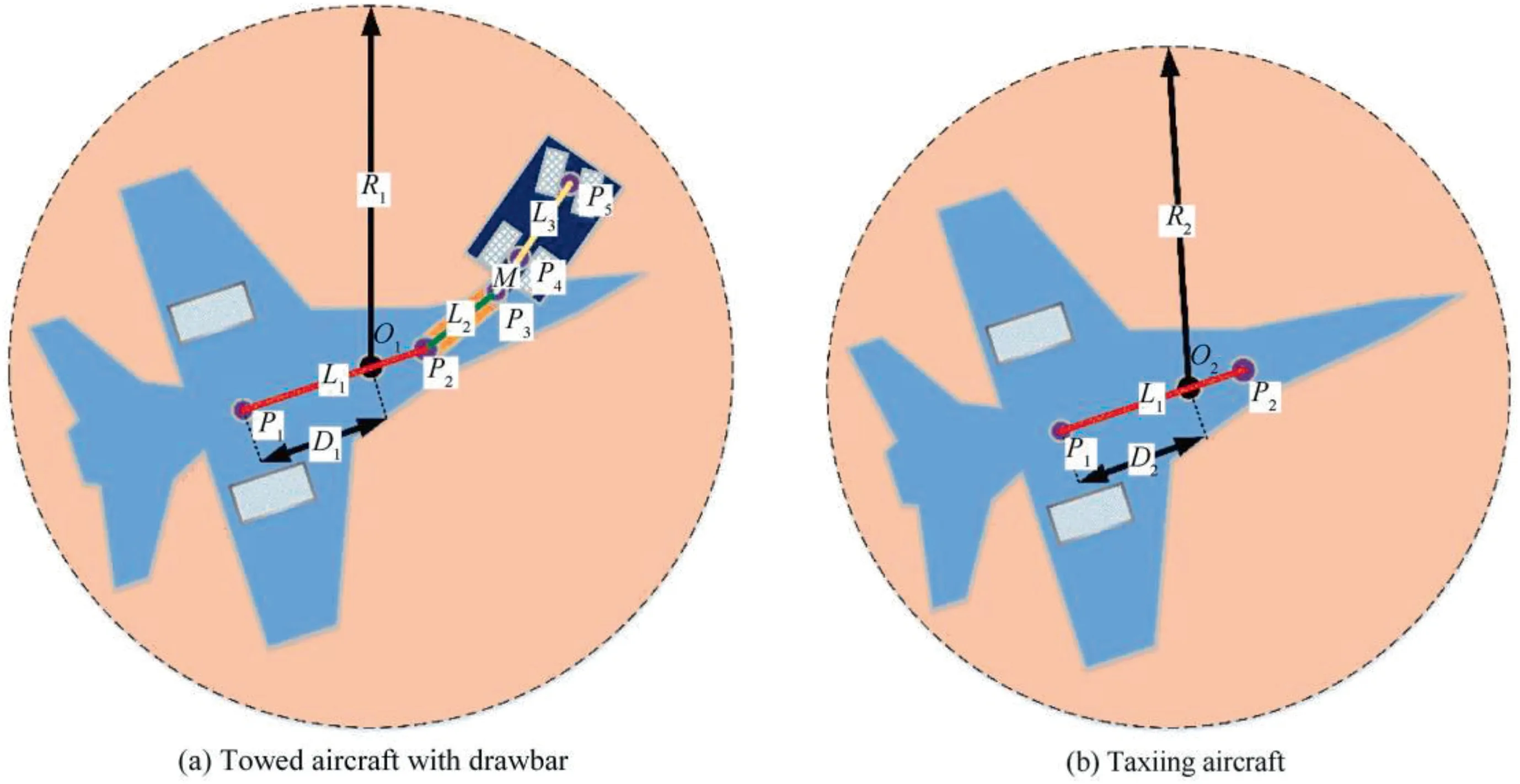
Fig. 1 Configurations of two typical dispatch systems on flight deck.

2.2. Cooperative trajectory planning for heterogeneous dispatch systems

Consider the cooperative trajectory planning problem where the numbers of involved towed aircraft systems and taxiing aircraft are nand n， respectively. Let n ＝n＋n. Then we formulate this problem into the following centralized optimal control problem

where xand yare the center location of the mth obstacle，aand bare its width and height， θrepresents the orientation，and pdetermines its shape.Ris the safe distance depending on the aircraft profile and safety requirement.

(2) For the ith and the jth dispatch systems （i≠j ）， collision avoidance between them are

3. Method

3.1. Homogenization and cooperative trajectory planning

It is seen from Section 2.1 that the kinematics of towed aircraft system and taxiing aircraft are different， with different statespace and constraints. Therefore， it’s difficult to describe the coordinated trajectory planning of these two systems under a unified framework. In addition， the dimension of state space of towed aircraft system is almost twice that of taxiing aircraft system. If the kinematic equation of towed aircraft system is directly used to carry out collaborative trajectory planning，the overall dimension of the solution will explode so that it’s hard to be solved directly.To improve the solution robustness and efficiency， cooperative trajectory planning for heterogeneous dispatch systems will be transformed into the problem of homogeneous ones.

To achieve the transformation， any towed aircraft system involved is abstracted into a virtual aircraft system， which is mainly composed of the aircraft from original towed aircraft system. Different from actual taxiing aircraft， the abstracted virtual aircraft can not only move forward like the taxiing system， but also implement reverse motion. In this way， all dispatch systems involved in trajectory planning can be described by the kinematics in Eq. (3). And the mechanical constraints can be written into the following uniform fashion.

where v＝0 m／s for taxiing aircraft，and v＝－vfor the virtual aircraft.

To solve the cooperative trajectory planning problem under the framework of optimal control， collision-free conditions，mechanical limit and other safe limit must be considered as constraints. For our problem， the constraints described in Eqs. (5)， (6) and (9) should be formulated into the fashion of h（x，u，t）≤0. The motion of taxiing aircraft and abstracted virtual aircraft are governed by the kinematics in Eq. (3).Additionally， the initial boundary conditions and the desired terminal boundary conditions are known.Hence，the cooperative trajectory planning problem can be described in the form of Eq.(4).By solving such an optimal control problem，the reference trajectory for each dispatch system is obtained.

3.2. Trajectory tracking based on RHC

Remark 1. As for a reference trajectory，the constraint in Eq.(5)ensures that the distance between a dispatch system and obstacle is no smaller than R， meanwhile the constraint in Eq. (6)guarantees that the distance between two dispatch systems is no smaller than 2R. However， during the actual trajectory tracking process， external disturbances may drive the dispatch system deviate from the reference trajectory and thereby lead to collision. Hence， we introducing the constraint in Eq. (11) to force the deviation keep within an acceptable range.

3.2.2.Optimal tracking control model for taxiing aircraft system

From the trajectory planning process， the motion information of taxiing aircraft systems can be obtained. When implementing the trajectory tracking， a different kinematic equation different from Eq. (3) is used. And it can be denoted as

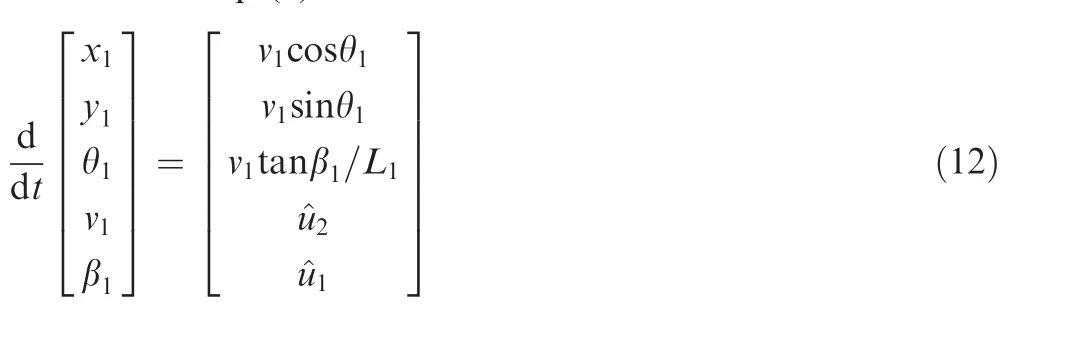
3.2.3. Online optimal tracking control method based on RHC

The actual trajectory and control for towed/taxiing aircraft system can be obtained by solving the optimal control model with an online optimal tracking control method based on RHC. The method can be summarized as follows.

3.3.Offline multi-objective optimization of weight parameters by using NSGA-II

The weight matrix P contains many coefficients in Eq. (10)，and the value of these coefficients will significantly affect the tracking performance. There are seven and five diagonal coefficients to be optimized for the towed aircraft system and the taxiing aircraft system， respectively. To ensure tracking accuracy and robustness， it’s necessary to optimize weight coefficients. For the trajectory tracking problem of the towed/taxiing aircraft system， the tracking performance can be evaluated by the following two indices:

(1)The tracking error of aircraft is the key to make the aircraft arrive at the destination efficiently and accurately，so the tracking error of aircraft is focus in this paper;

(2)The control variables of the system should be smooth so that the results can facilitate engineering applications， so the magnitude of control variables should be minimized.

Based on the above two indices， this paper considers the following three objectives to be optimized:

There are typically two types of algorithm to solve the multi-objective optimization problem. The one is based on mathematical programming method and the other is based on genetic algorithm. Among many multi-objective optimization genetic algorithms， NSGA-II algorithmis the most mature and has been widely used.It can find the optimal solution set that makes each objective function is close to the maximum or minimum as much as possible. During the optimization process， external disturbances as illustrated in Remark 2 is introduced to simulate actual operation.The flowchart of weight optimization can be summarized as follows:

Step 1. Initialize parameters of NSGA-II， including the population size and the number of maximum generation.And Generate the initial population P.

Step 2. Using each individual in Pto solve the online tracking problem described in Section 3.2.3 and record the trajectory and corresponding control.

Step 3. According to the results of Step 2， calculate the objective function defined in Eq. (15).

Step 4. If the number of the maximum generation is met，output the best individual in P; otherwise， update Paccording to NAGA-II and return to Step 2.

Remark 3. In the process of weight optimization， the computation cost/complexity is closely related to the selection of parameters in the NSGA-II algorithm. For example， a large population size and a big maximum generation usually result in a high computational time. However， the computational burden of the weight optimization process is not considered in this paper since it is an offline process. Once the weights are determined in advance，the tracking control model of the same type of system (taxiing or towing system) is fixed. The work remained is to track each reference trajectory provided by the trajectory planning module by the RHC，and the offline weight optimization process introduces no computational burden into the online computation process.

3.4. Overall control strategy

Finally， by integrating the weight optimization process with the HPT method，an overall diagram of the autonomous cooperative dispatch control is illustrated in Fig. 2.

4. Simulation

4.1. Environment description and parameter settings

We set a scenario where five aircraft are involved，and their initial and terminal desired postures are listed in Table 1. Eachaircraft is considered to be parked at initial positions with a zero front wheel steering angle.And they are expected to completely stop at the terminal posture with a zero front wheel steering angle. Among the five aircraft， two aircraft are dispatched by taxiing (denoted as type 0) and the other three are dispatched by a towing system(denoted as type 1).Related geometric parameters are given as L＝6 m， L＝4 m，L＝2 m and M ＝1 m. The radius of featured circle of taxiing aircraft and towed aircraft system at set as 9 m and 11 m， respectively.

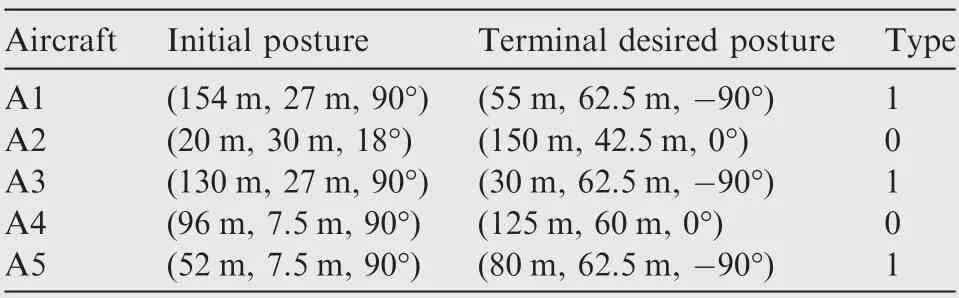
Table 1 Initial and terminal desired postures of five aircraft.

There are two obstacles (i.e.， O1 and O2) in the environment， and their geometric parameters are given in Table 2.And the safe distance is set as R＝1 m. Thus， collisionfree conditions can be obtained according to Eqs. (5)-(6).

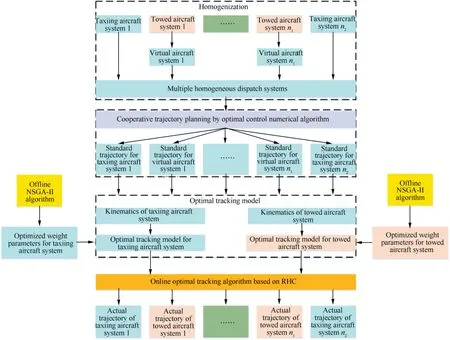
Fig. 2 Flowchart diagram of the HPT method integrated with weight optimization process.

Table 2 Information of two obstacles.

In the trajectory planning process， the limits on state and control variables are restrained more tightly when compared to the subsequent tracking process. The reasons are twofold.On the one hand，disturbances exist in real world.On the other hand，in particular for towed aircraft system，a virtual aircraft is used for trajectory planning.The actual trajectory will overwhelmingly deviate from the reference trajectory due to disturbances and model mismatch. Hence， slight tighter mechanical constraints would facilitate a perfect trajectory tracking.

As for taxiing aircraft (i.e.， A2 and A4)， mechanical constraints are given as

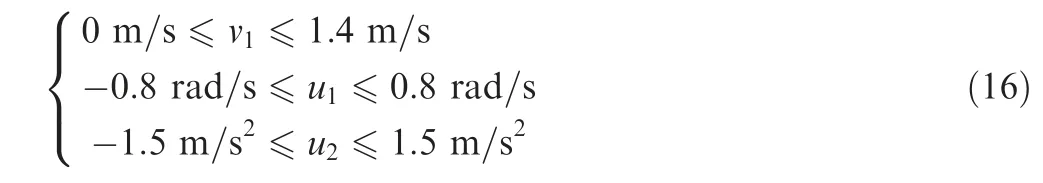
As for virtual aircraft adapted form towed aircraft systems，constraints on velocity in Eq. (16) is replaced by－1.4 m／s ≤v≤1.4 m／s.

4.2. Cooperative trajectory planning

4.2.1. Benefit of the homogenization strategy

The idea of homogenization can reduce the dimensions of solution and simplify the original problem; however， the improvement of computational efficiency and robustness needs further verification. In this section， 19 scenarios as listed in Table 3 are tested. Both the homogenization strategy and the non-homogenization strategy are adopted，and their computational efficiency are reported.

From Table 3， we can see that the cooperative trajectory planning experiment based on homogenization can be successfully applied to all 19 scenarios.When the number of dispatch system get bigger， the non-homogenization strategy shows its deficiency in computational efficiency.For the scenarios where both two methods converge， the computational efficiency based on the homogenization is obviously higher than that based on non-homogenization， with a more than 80%improvement on average. It suggests that the method based on homogenization can greatly improve the efficiency and robustness of collaborative trajectory planning.

4.2.2. Cooperative trajectory planning based on homogenization

In this section， the cooperative trajectory planning for all five dispatch systems are considered. According to the HPT method， the aircraft A1， A3， A5 will be abstracted into a virtual aircraft system. The formulated optimal control problem is solved by the pseudospectral algorithm and the convergent tolerance is set as 1E-5. The converged terminal time is 112.15 s and the corresponding trajectories are given in Fig.3.Fig.3 shows that all five trajectories are smooth.However，the collision with obstacles and other dispatch systems for all these trajectories should also be verified.Therefore，the following two indexes are proposed in this paper to describe it.

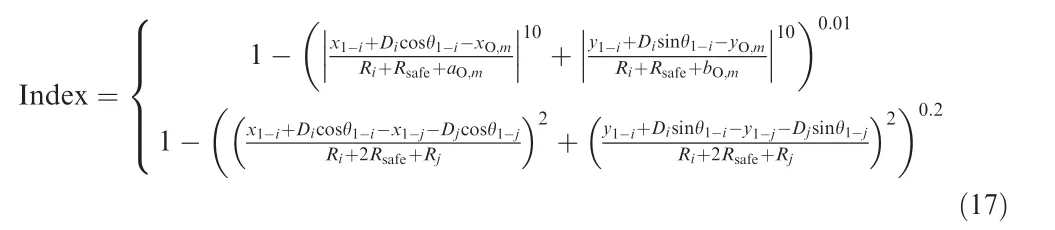
According to Eq.(17)，if Index ≤0，the collision avoidance is achieved; otherwise， the collision occurs. The avoidance index between dispatch systems and obstacles， as well as theavoidance index within dispatch systems， are shown as Fig. 4.The maximum value of Index in Fig. 4 is－4.6385×10，which is smaller than 0. Hence， the collision avoidance is achieved for all obtained trajectories.

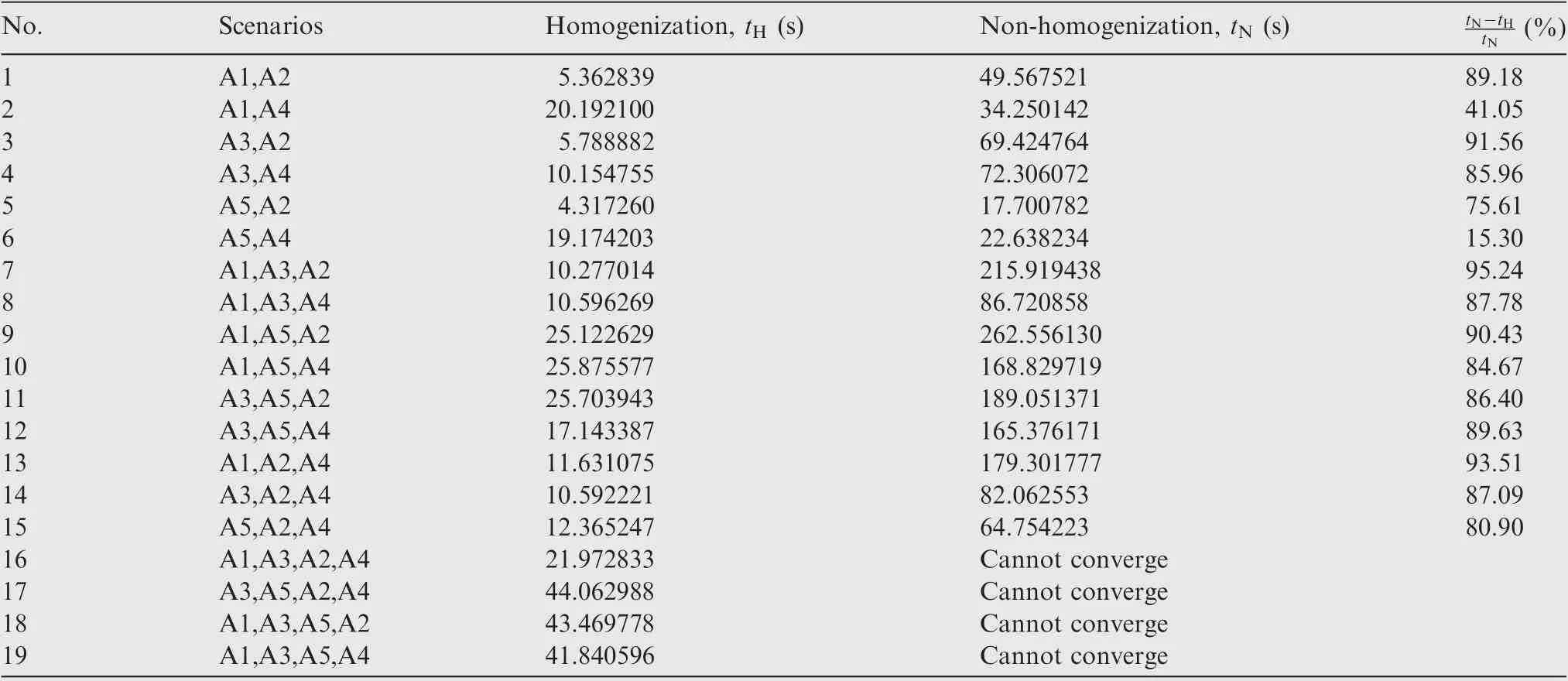
Table 3 Computational efficiency with/without the homogenization strategy.

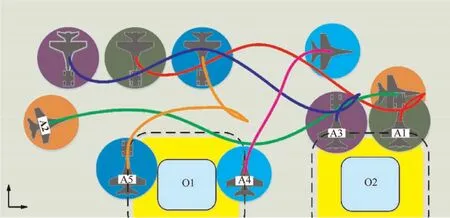
Fig. 3 Trajectory for the homogeneous aircraft systems.

The velocity and control corresponding to the optimal trajectory are shown in Fig. 5. It is seen that the profiles of these variables are smooth and strictly restrained within the allowable range. All five aircraft come to a completely full stop at the terminal time.

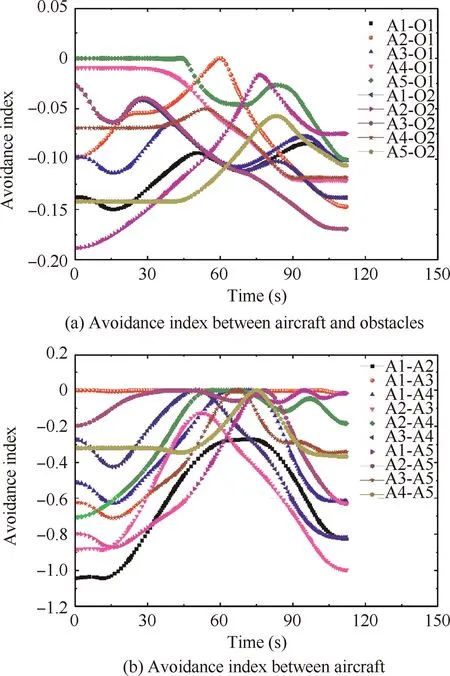
Fig. 4 Avoidance index of the multiple homogeneous systems.

Combining Fig. 3 and Fig. 5， some interesting phenomena can be found.Since the initial positions of A1 and A3 are adjacent， their trajectories keep close to each other during the entire dispatch process. In addition， A5 does not set off until A2 has passed in the front. It indicates that the algorithm has good coordination capability for multiple agents.

4.3. Trajectory tracking based on RHC

4.3.1. Parameter settings

The RHC technique is used to track the reference obtained in Section 4.2. For both two types of dispatch systems， the sampling period is set as δT ＝0.1 s and the prediction window length is set as T ＝8 s. For open-loop optimal control problems to be solved at each sampling instant， they are solved by the SPM with 10 LGL nodes and the convergent tolerance 1.0 ×10.

Fig. 5 Velocity and control of the standard optimal trajectory.

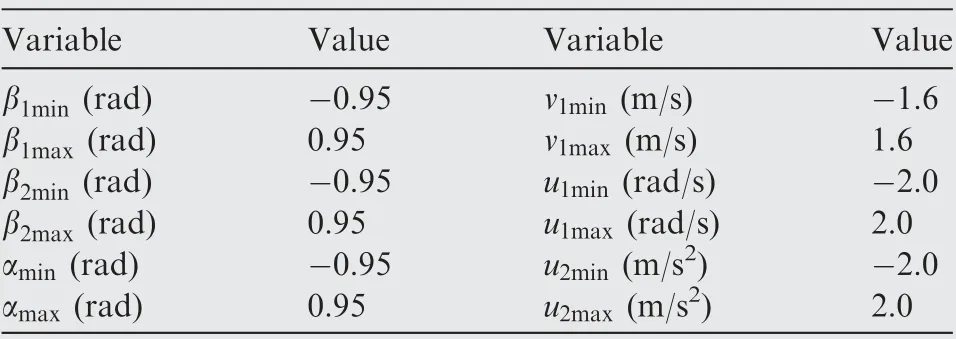
Table 4 Mechanical constraints applied in the RHC for towed aircraft systems.

4.3.2. Trajectory tracking for towed aircraft systems

It is seen in Fig. 6(a) that the position error is always kept below 0.8 m.Hence，Eq.(11)is satisfied，which further demonstrating that the collision avoidance is achieved. The terminal tracking error for three towed aircraft systems are reported in Table 5，suggesting a good satisfaction on terminal states.Profiles for other state variables are given in Fig. 7-Fig. 8， and Fig.9 exhibits the control input.It is seen that mechanical constrains imposed are perfectly satisfied.

Since a towed aircraft system is controlled by the tractor，it’s necessary to get the tractor velocity and steering angle of front wheel. Related information is reported in Fig. 10.

Table 5 Terminal tracking errors for A1， A3 and A5.

4.3.3. Trajectory tracking for taxiing aircraft systems

Fig. 7 Motion information of towed aircraft systems.

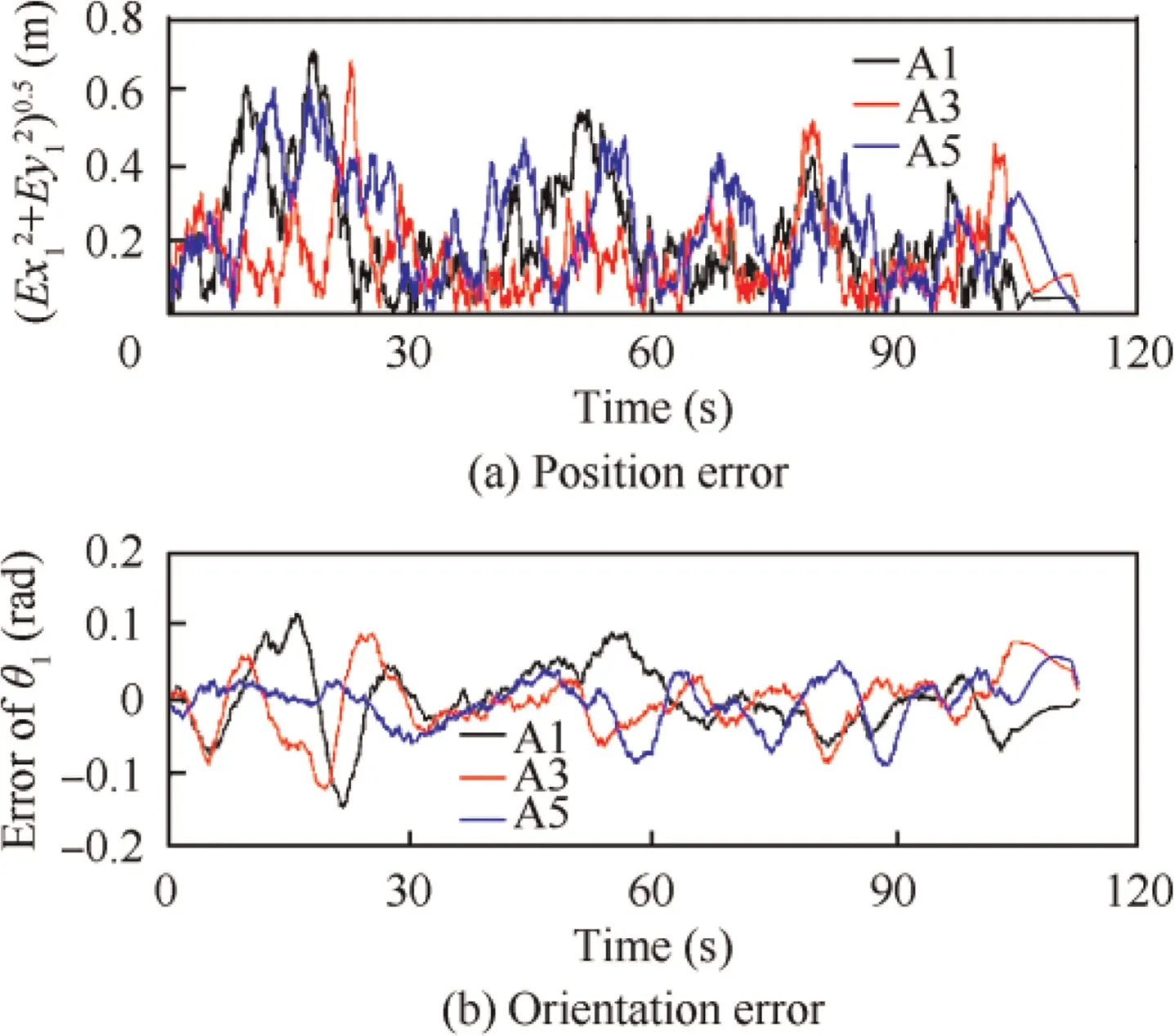
Fig. 6 Tracking error of towed aircraft systems.

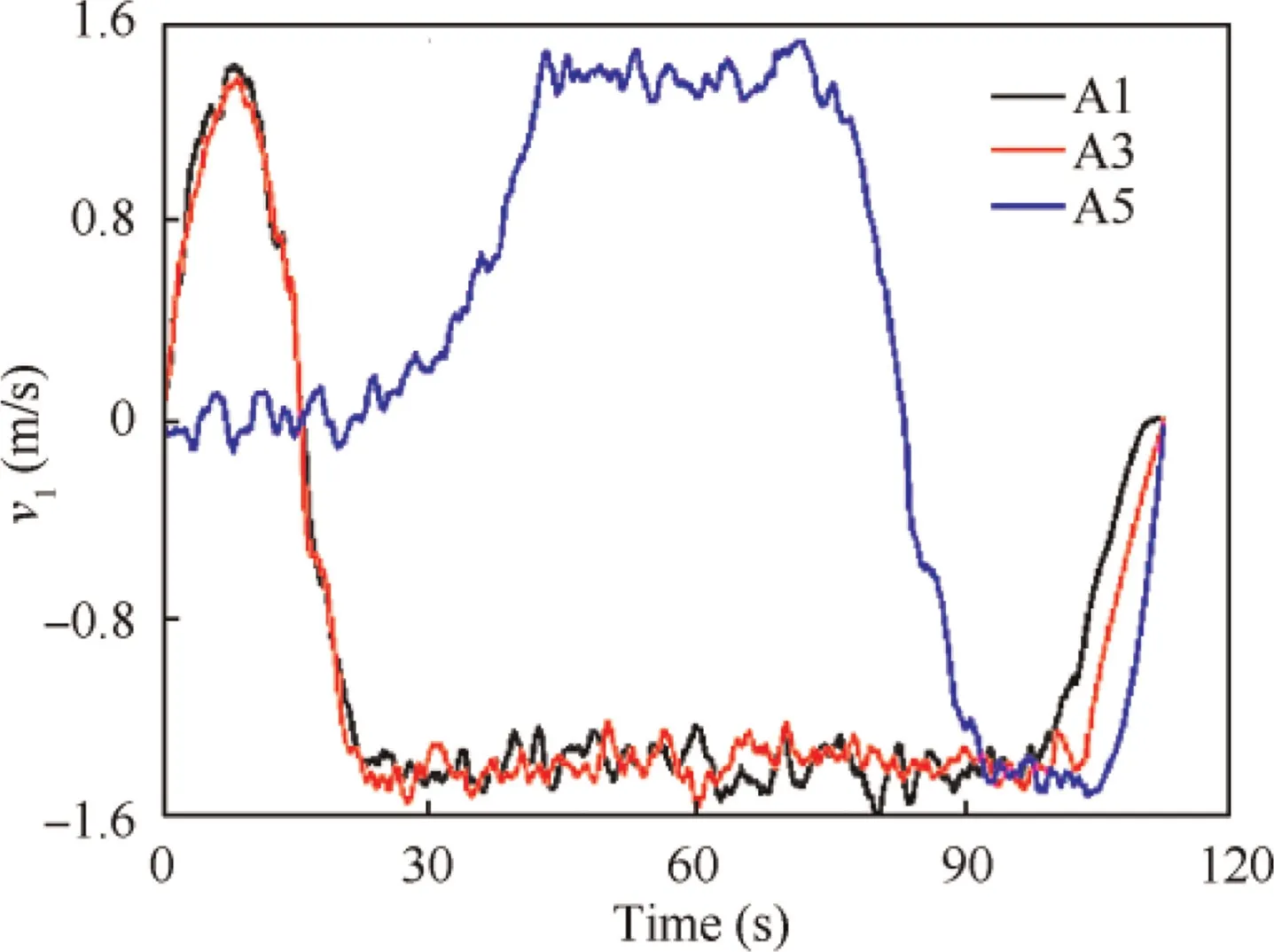
Fig. 8 Velocity of the aircraft.

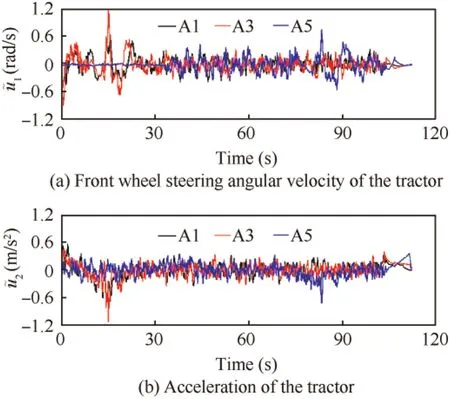
Fig. 9 Control of towed aircraft systems.

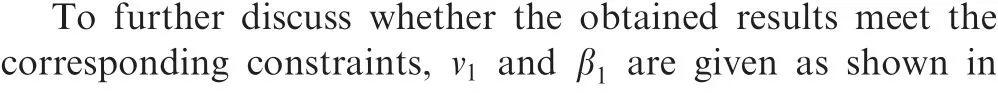
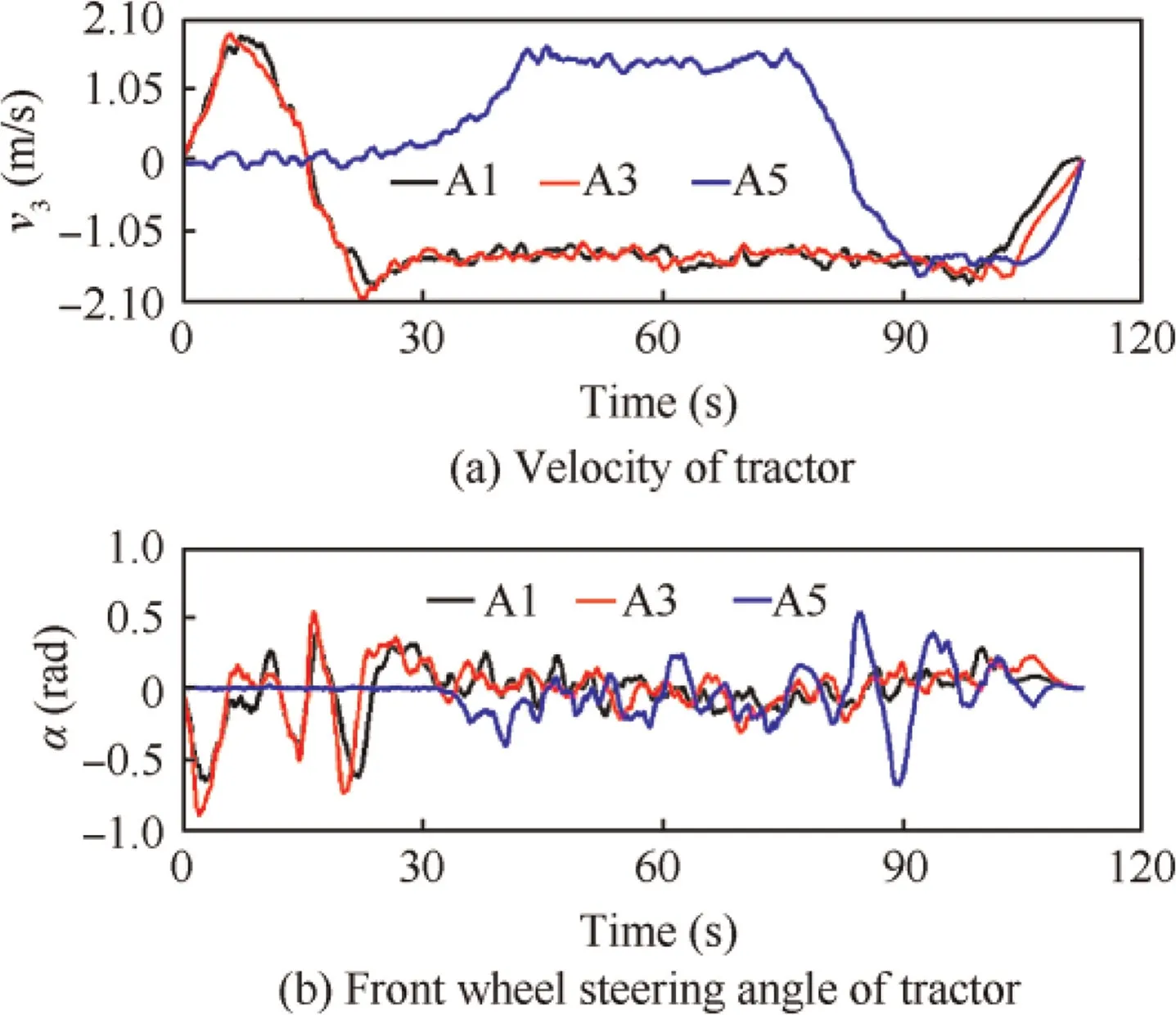
Fig. 10 The velocity and steering angle for tractor.

Table 6 Mechanical constraints applied in RHC for taxiing aircraft systems.

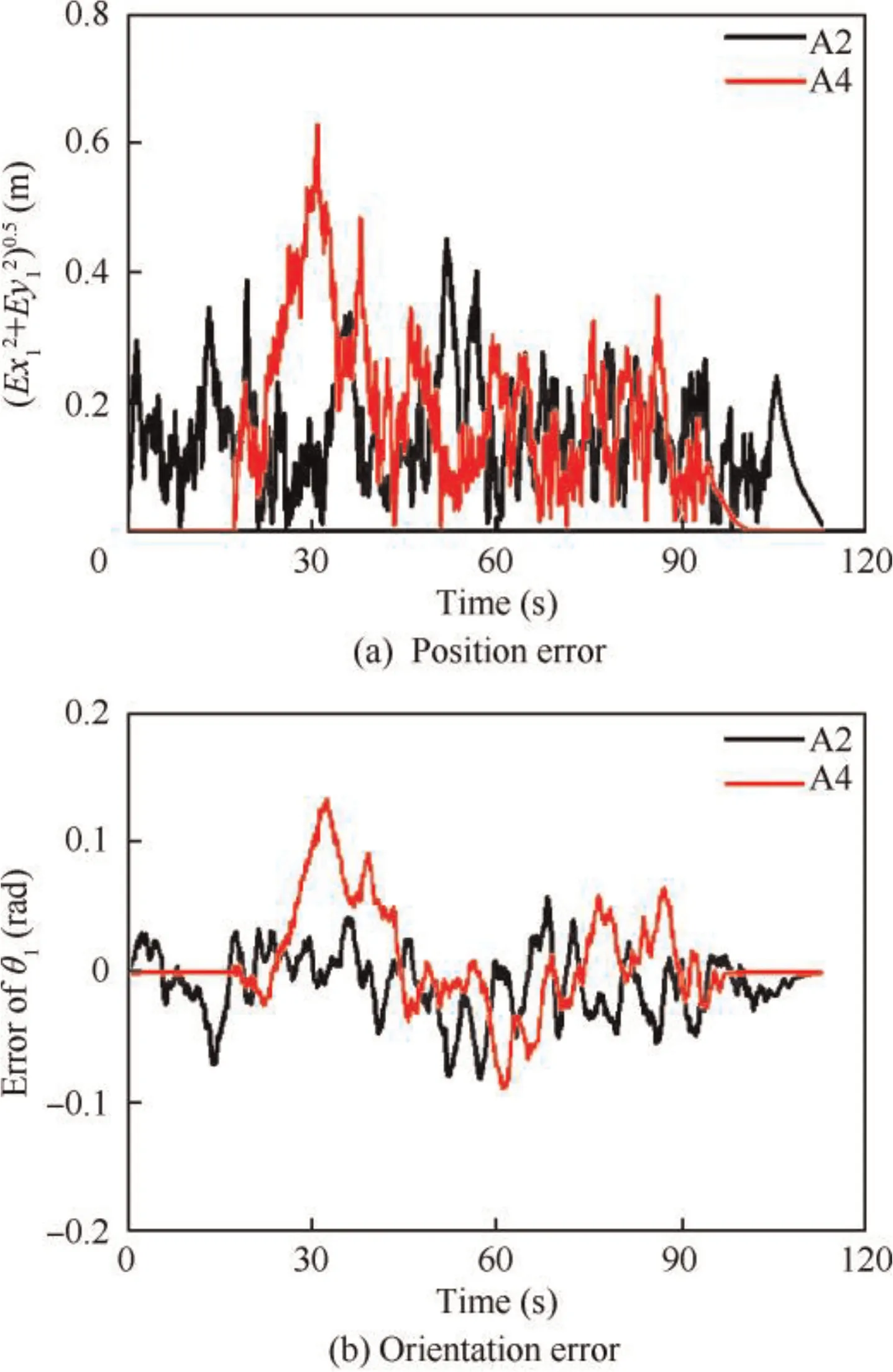
Fig. 11 Tracking error of taxiing aircraft systems.

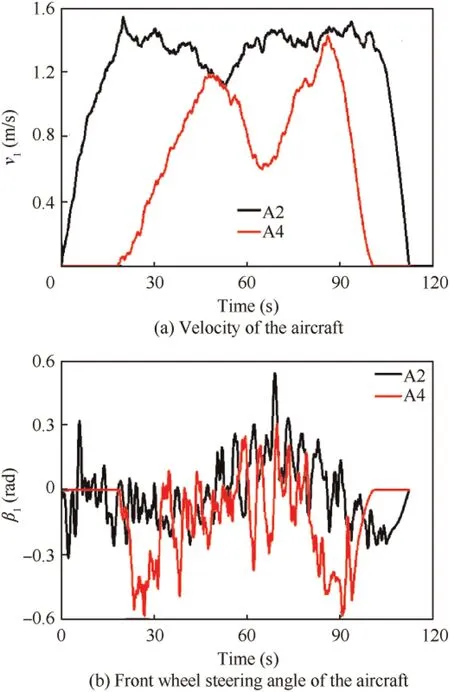
Fig. 12 Motion information of taxiing aircraft systems.

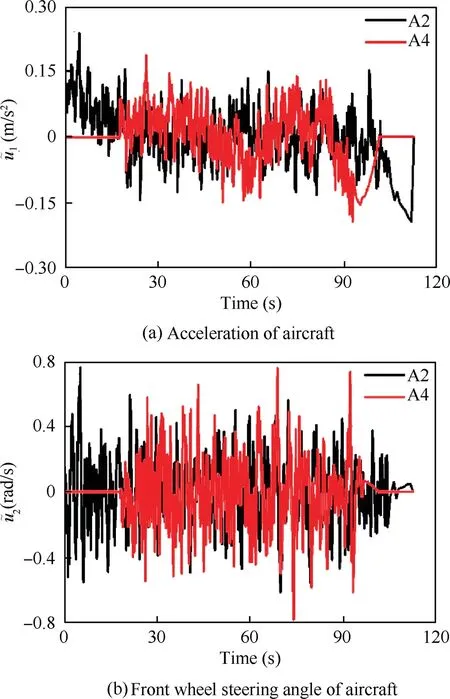
Fig. 13 Control of taxiing aircraft systems.

5. Conclusions

This paper proposed HPT method to solve the cooperative trajectory planning and control for heterogeneous carrier aircraft systems. The cooperative trajectory planning problem is formulated as a centralized optimal control problem where any towed aircraft system involved is simplified into a virtual taxiing aircraft. Such an operation transforms the original problem into a trajectory planning problem for homogeneous system. Since the scale and nonlinearity of the formulated problem is reduced， the computational robustness and efficiency can be guaranteed. When the reference trajectories are obtained，the RHC technique is applied for trajectory tracking.To further improve the tracking performance， the multiobjective optimization technique is integrated to determine the optimal combination of weighted parameters.

Kinematic models are used in the proposed trajectory tracking controller. As pointed in Ref. 4， kinematic models cannot reflect complex dynamic behaviors of the dispatch systems， and the dynamic models are recommended. However，either taxiing aircraft or towed aircraft system is a underactuated system with nonholonomic constraints. During the practical implementation， dead zone and uncertainty in system parameters may occur.In addition， a precise information on all state variables is the prerequisite to implement the RHC.Once a part of the state variables cannot be measuredly directly or accurately estimated by state estimation techniques，advanced control methods must be developed.The autonomous dispatch control on flight deck is a complex and huge systems engineering， while trajectory planning is just the tip of the iceberg.Hence，our future work is to develop a practical trajectory tracking controller on the basis of dynamic models.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

The authors are grateful for the National Key Research and Development Plan， China (No. 2019YFB1706502); the National Natural Science Foundation of China (Nos.62003366， 12102077， 12072059); the China Postdoctoral Science Foundation (No. 2020M670744); the Natural Science Foundation of Liaoning Province，China(No.2010-ZD-0021).