A novel imprecise stochastic process model for time-variant or dynamic uncertainty quantification

Jinwu LI， Chao JIANG

State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body， College of Mechanical and Vehicle Engineering， Hunan University， Changsha 410082， China

KEYWORDS Dynamic reliability analysis;Epistemic uncertainty;Imprecise random variable;Imprecise stochastic process;P-box model;Time-variant uncertainty

Abstract This paper proposes a novel model named as ‘‘imprecise stochastic process model” to handle the dynamic uncertainty with insufficient sample information in real-world problems. In the imprecise stochastic process model，the imprecise probabilistic model rather than a precise probability distribution function is employed to characterize the uncertainty at each time point for a time-variant parameter， which provides an effective tool for problems with limited experimental samples. The linear correlation between variables at different time points for imprecise stochastic processes is described by defining the auto-correlation coefficient function and the crosscorrelation coefficient function. For the convenience of analysis， this paper gives the definition of the P-box-based imprecise stochastic process and categorizes it into two classes: parameterized and non-parameterized P-box-based imprecise stochastic processes.Besides，a time-variant reliability analysis approach is developed based on the P-box-based imprecise stochastic process model，through which the interval of dynamic reliability for a structure under uncertain dynamic excitations or time-variant factors can be obtained. Finally， the effectiveness of the proposed method is verified by investigating three numerical examples.

1. Introduction

Uncertainties exist extensively in real-world problems， such as materials properties， geometric parameters， boundary conditions and loads applied on a structure.In traditional probability theory， these uncertain parameters are generally described using probabilistic model and the corresponding uncertainty analysis is carried out within the probability statistics framework.Currently，the probability method has been well studied in varieties of areas， including uncertainty quantification，uncertainty propagation，structural reliability analysis，Reliability-Based Design Optimization (RBDO)and stochastic dynamics analysis.The premise for investigation of the above uncertainties using the probability method is that the precise probability distribution functions of uncertain parameters are available， which generally needs huge amounts of experimental samples. However， because of limitations in testing environment or cost，it is often difficult or even impossible to acquire adequate high-quality experimental samples to construct the precise probability distribution information，namely，there exists the epistemic uncertainty problem in this situation.

Therefore， in recent years the imprecise probabilistic modelhas been proposed to represent parametric uncertainty under conditions with insufficient sample information.Compared with the traditional probabilistic model，the imprecise probabilistic model can describe both the aleatory and epistemic uncertainties of a parameter. The existing imprecise probabilistic models mainly include Bayesian theory，probability box (P-box) model，random sets，Dempster-Shafer’s theory of evidenceand fuzzy randomness.So far the imprecise probabilistic model and corresponding methods have been applied in many fields， including uncertainty propagation， reliability analysis and RBDO.

The objective of uncertainty propagation for imprecise probability is to obtain characteristic parameters of a response function with imprecise probabilistic variables. Williamson and Downspresented a convolution method for arithmetic operations of P-box variables.Bruns and Paredisintroduced a P-box Convolution Sampling (PCS) method to propagate imprecise uncertainty for black-box models. Ghosh and Olewnikproposed a sparse grid numerical integrationbased imprecise uncertainty propagation analysis approach.Scho¨bi and Sudretproposed a two-level meta-modelling approach for propagating P-box uncertainty by surrogating the precise computational model with the sparse polynomial chaos expansions model. Liu et al.combined the univariate dimension reduction method with Johnson distributions fitting，through which bounds of statistical moments and Cumulative Distribution Function(CDF)of a response function can be obtained efficiently. Zhang and Shieldsproposed a methodology for uncertainty propagation of imprecise probabilities based on the Bayesian inference.Wei et al.proposed a non-intrusive imprecise stochastic simulation method to propagate imprecise uncertainties.

To carry out the safety evaluation under imprecise uncertainties， the corresponding structural reliability analysis approaches have been developed in this field. Utkin and Kozinedescribed several new imprecise structural reliability models based on the imprecise Bayesian inference. Zhangused an importance sampling technique to generate point samples for imprecise probability functions， through which the reliability bounds of a structure can be obtained. Based on the P-box model and the Copula theory， Zhang et al.proposed an imprecise probability modeling approach for the atmospheric corrosion of steel structures when lacking sufficient information and perform the corresponding reliability analysis for steel structures. Chabridon et al.compared two different approaches for the aerospace system reliability assessment under epistemic uncertainties， namely， the nested and augmented approaches. Wang et al.translated the problem for computing the reliability bounds for structures with imprecisely known random variables into a series of linear programming problems. Gao et al.investigated the reliability assessment for engineering structures with spatial uncertainty described using imprecise random and interval fields.Khakzaddeveloped an approach for system safety assessment using imprecise probabilities in the Bayesian network.Faes et al.determined the bounds on the first excursion probability of a linear structure under an imprecise stochastic load.The reliability index or its interval can be obtained through the above analysis， which can provide beneficial guidance for the safety evaluation of a structure involving imprecise uncertainties.

By setting the reliability indexes as constraint conditions， a series of RBDO approaches have been proposed in the imprecise probability community.Mourelatos and Zhouproposed an Evidence-Based Design Optimization (EBDO) method for reliability-based optimization problems with aleatory and epistemic hybrid uncertainties. Youn and Wangdeveloped a Bayesian RBDO methodology based on eigenvector dimension reduction method. Srivastava and Debproposed a generalized Bayesian reliability-based design optimization algorithm using the Bayesian inference to quantify design reliability. Srivastava et al.proposed a bi-objective evolutionary algorithm-based approach for design optimization using the evidence theory. Zaman and Mahadevanproposed formulations and algorithms for RBDO of both single and multidisciplinary systems under both aleatory and epistemic uncertainties. Zhang et al.developed an improved twostage framework to handle the EBDO problem under epistemic uncertainty. Wang et al.investigated the RBDO for multidisciplinary problems involving interval and fuzzy uncertainties.

So far a series of important developments have been made in the imprecise probability analysis community.However，the above methods and techniques under the imprecise probability framework are mainly utilized to handle time-invariant or static problems. Nevertheless， some uncertain parameters have time-variant or dynamic characteristics in plenty of practical problems. For instance， wave impact loads acting on ocean platforms and surface temperature of satellite installations，not only exhibit uncertainties， but also change with time.

At present， the dominating approach to handle timevariant or dynamic uncertainties is to model them using the classical stochastic process theory which has been widely applied in many fields，such as uncertainty propagation analysisand time-variant reliability analysis.When using the stochastic process model， nevertheless， the precise probability distribution function at an arbitrary time point must be constructed based on massive high-quality testing samples.However， in plenty of real-world situations owing to the limitations in testing environment or cost，it is also hard to obtain enough samples to construct precise probability distribution functions for dynamic uncertain parameters， that is to say，there exists the epistemic uncertainty problem in these situations. Moreover， the uncertainty quantification and analysis in the time-variant problems are much more difficult than general static problems since all of the time points should be considered in the former. Thus， how to effectively handle timevariant or dynamic epistemic uncertainty problems has become a difficult and frontier issue in the uncertainty analysis field，which is vital for whole lifecycle reliability design of complex structures or systems.

This paper， therefore， extends the general imprecise probability theory into time-variant problems to develop a novel imprecise stochastic process model for quantification of timevariant or dynamic uncertainties.The imprecise stochastic process model is expected to be a supplement for the classical stochastic process model to effectively deal with the epistemic uncertainty in time-variant problems. The remainder of this paper is organized as follows: Section 2 gives the definitions and corresponding mathematical fundamentals of the imprecise stochastic process theory. Section 3 gives the definitions and classification of the P-box-based imprecise stochastic process. Section 4 applies the P-box-based imprecise stochastic process to the structural time-variant reliability analysis. Section 5 investigates three numerical examples. Section 6 draws conclusions of this paper.

2. Imprecise stochastic process model

As stated previously， there exist a lot of time-variant or dynamic uncertainty problems in practical engineering. In order to handle the epistemic uncertainty problems owing to lack of samples or low-quality samples， etc.， we develop a novel mathematical model for time-variant uncertainty quantification by introducing the imprecise probabilistic model into the classical stochastic process theory， namely， the imprecise stochastic process model. Different from the classical stochastic process theory，our imprecise stochastic process employs an imprecise random variable instead of a precise CDF to characterize uncertainty degree at an arbitrary time point for a timevariant parameter. The definitions and mathematical fundamentals of the imprecise stochastic process model are given as follows.

It should be pointed out that we can use any type of imprecise probabilistic model such as P-box， random sets and Dempster-Shafer’s theory of evidence， to deal with the parametric uncertainty at a single time point theoretically; we can even use different imprecise probabilistic models to deal with the parametric uncertainties at different time points of a time-variant parameter. In the imprecise stochastic process model，actually the epistemic uncertainty is addressed by introducing the imprecise random variable while the time-variant uncertainty is described through the analysis framework of the traditional stochastic process.Hence the imprecise stochastic process model can deal with the time-variant epistemic uncertainty problem effectively.

3. P-box-based imprecise stochastic process

The existing imprecise probabilistic models mainly include Bayesian theory，P-box model，random sets，Dempster-Shafer’s theory of evidenceand fuzzy randomness.The P-box is an important imprecise probabilistic model and mainly used for uncertainty quantification of time-invariant parameters when lacking sufficient information.Due to its convenience to understand and distinct processing function for the epistemic uncertainty， the P-box model has been attracting growing attention and applied in many fields in recent years.For the convenience of analysis， we only take the P-box model as an example to elaborate the imprecise stochastic process model in this paper.

3.1. General P-box model

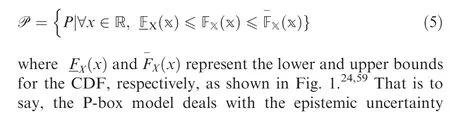
Fig. 1 CDF bounds of a P-box variable.24，59

For an uncertain variable X in practical engineering problems，we usually use a CDF F（x ） to quantify its uncertainty. For the P-box model， X is quantified by a pair of bounds of the CDF:owing to the lack of sufficient samples by introducing a pair of bounds of the CDF. For the convenience of distinguishing and reading， this paper uses X and Xto denote random and P-box variables， respectively.

At present， P-boxes are generally categorized into two classes， namely， the parameterized and the nonparameterized P-boxes.The parameterized one is the class of P-box whose distribution type is deterministic and distribution parameters are described by interval model. The parameterized P-box Xcan be expressed as:

3.2. Definition of P-box-based imprecise stochastic process

3.3. Parameterized P-box-based imprecise stochastic process

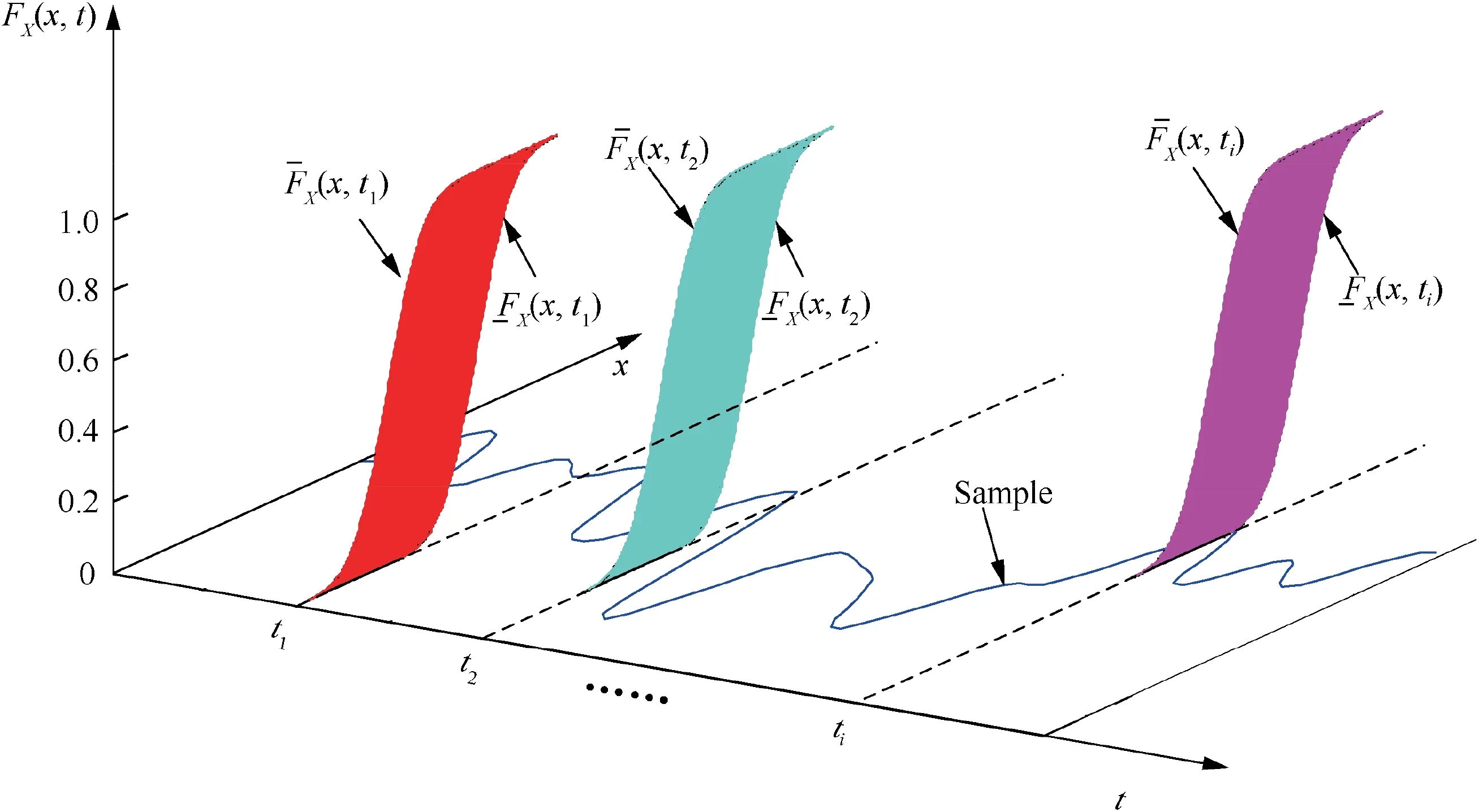
Fig. 2 A P-box-based imprecise stochastic process.

In Definition 7， the distribution parameter vector θ（t ） is related to the time t and hence can be treated as a function vector of the time t， denoted as distribution parameter function vector.Meanwhile，the lower bound function vector and upper bound function vector of the distribution parameter function vector are denoted as θ（t ） and θ（t ）， respectively. When the lower bound function vector and upper bound function vector of the distribution parameter function vector of a parameterized P-box-based imprecise stochastic process X（t ）are equal to each other，namely，θ（t ）＝θ（t ）＝θ（t ），X（t ）will degenerate into a stochastic process X（t ）.

Definition 8. For a parameterized P-box-based imprecise stochastic process X（t ）， if the distribution type at an arbitrary time point of X（t ） is Gaussian distribution， namely:

3.4. Non-parameterized P-box-based imprecise stochastic process

then X（t ） is called as stationary non-parameterized P-boxbased imprecise stochastic process.

The non-parameterized P-box-based imprecise stochastic processes which do not satisfy Definition 12 are termed as non-stationary non-parameterized P-box-based imprecise stochastic processes.

4. Application in structural time-variant reliability analysis

Fig. 3 A stationary non-parameterized P-box-based imprecise stochastic process.

Step 3.Calculate the reliability under the given distribution parameter function vector Θ（t ） within the time interval ［0，T］using the Monte Carlo simulation method.

Step 4. Repeat the operation of Step 2-Step 3 for several times and obtain the lower and upper of the reliability with the time interval ［0，T］.

For the convenience of programming， this paper also gives the calculation flow and the corresponding flow chart of the above two-layer MCS method in the Appendix.

5. Numerical examples and discussions

In order to demonstrate the effectiveness of the proposed method， this section applies the P-box-based imprecise stochastic process model and the corresponding time-variant reliability analysis method to three numerical examples. The first one is a response function problem， the second one is the ten-bar truss problem and the final example is a Printed Circuit Board (PCB) module problem based on the finite element analysis.

5.1. A response function problem

Consider a structure whose performance function is a response function as follows:

Fig. 4 Bounds of the reliability over 0–10 years under different auto-correlation coefficient functions.

Secondly， the effect of the value of the threshold h on dynamic reliability is researched. Consider four cases for the threshold: (a) h ＝0.0; (b) h ＝0.5; (c) h ＝1.0 and (d)h ＝1.5. By using the proposed method with 10samples in its inner layer MCS and 10samples in its outer layer MCS，the lower and upper bounds of the reliability over 0–10 years under different thresholds are computed and plotted，as shown in Fig.5.First，the reliability at each design lifetime is a deterministic value when h ＝0.0， as shown in Fig. 5(a)， which is because the mean function of the response function is always 0 when the threshold h ＝0.0. Second， the reliability at each design lifetime is an interval when h is not equal to 0 and the interval of reliability at the initial time under the remaining three different thresholds are [0.6012， 0.6951]， [0.6951，0.8453] and [0.7733， 0.9378]， respectively， as shown in Fig. 5(b)-(d). Third， as the threshold increases， both the lower and upper bounds of the reliability within a certain design lifetime increase，as shown in Fig.5(e).This result is consistent with the phenomenon in real-world engineering problems.

5.2. A ten-bar truss structure

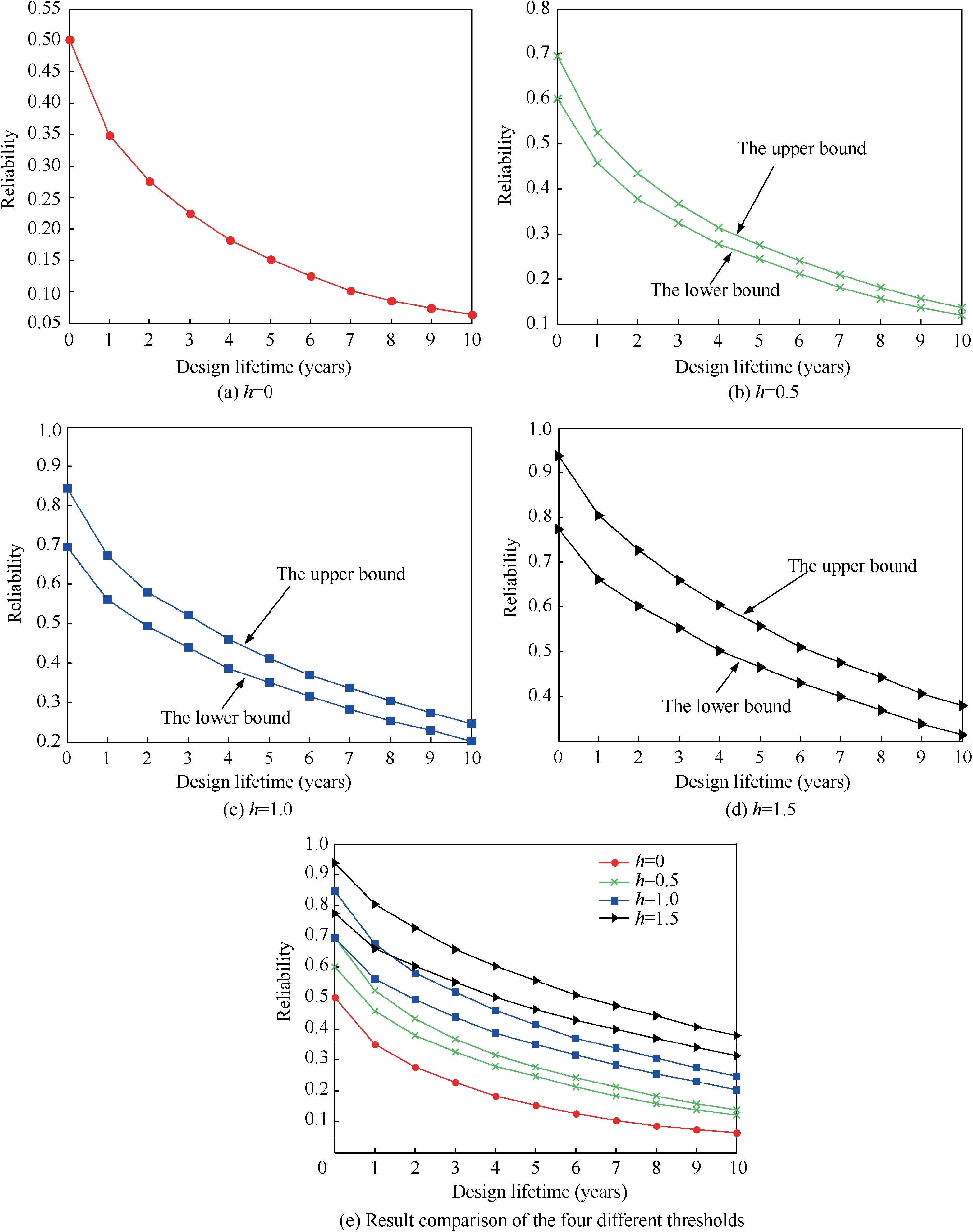
Fig. 5 Bounds of the reliability over 0–10 years under different thresholds.

Fig. 6 A ten-bar truss structure.70

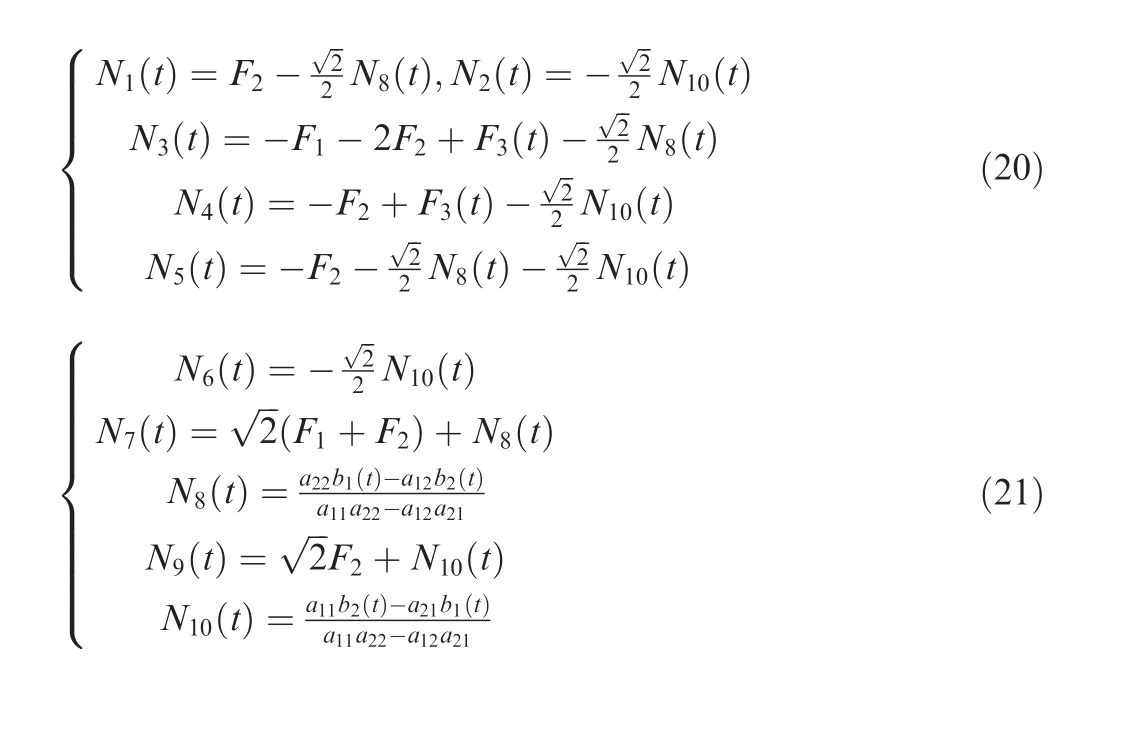
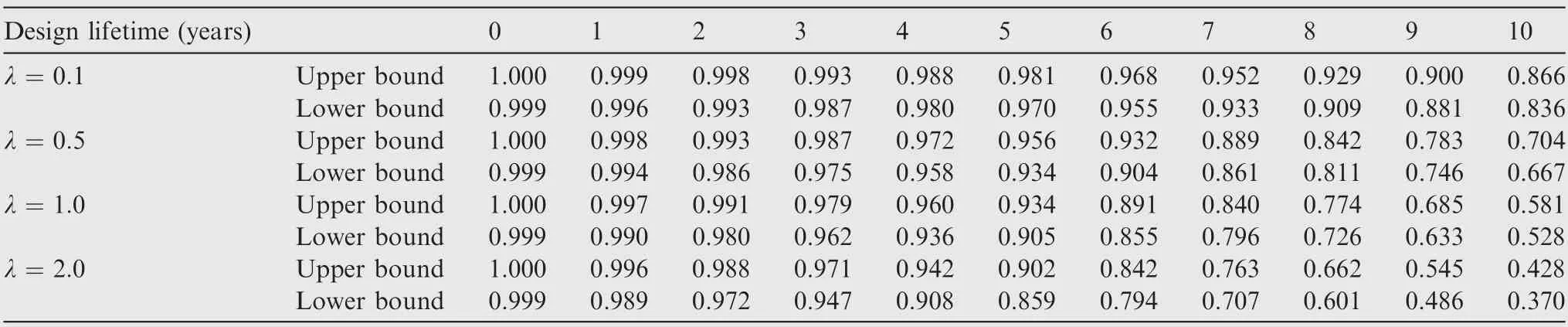
Table 1 Reliability of the ten-bar truss structure over 0–10 years under different values of λ.

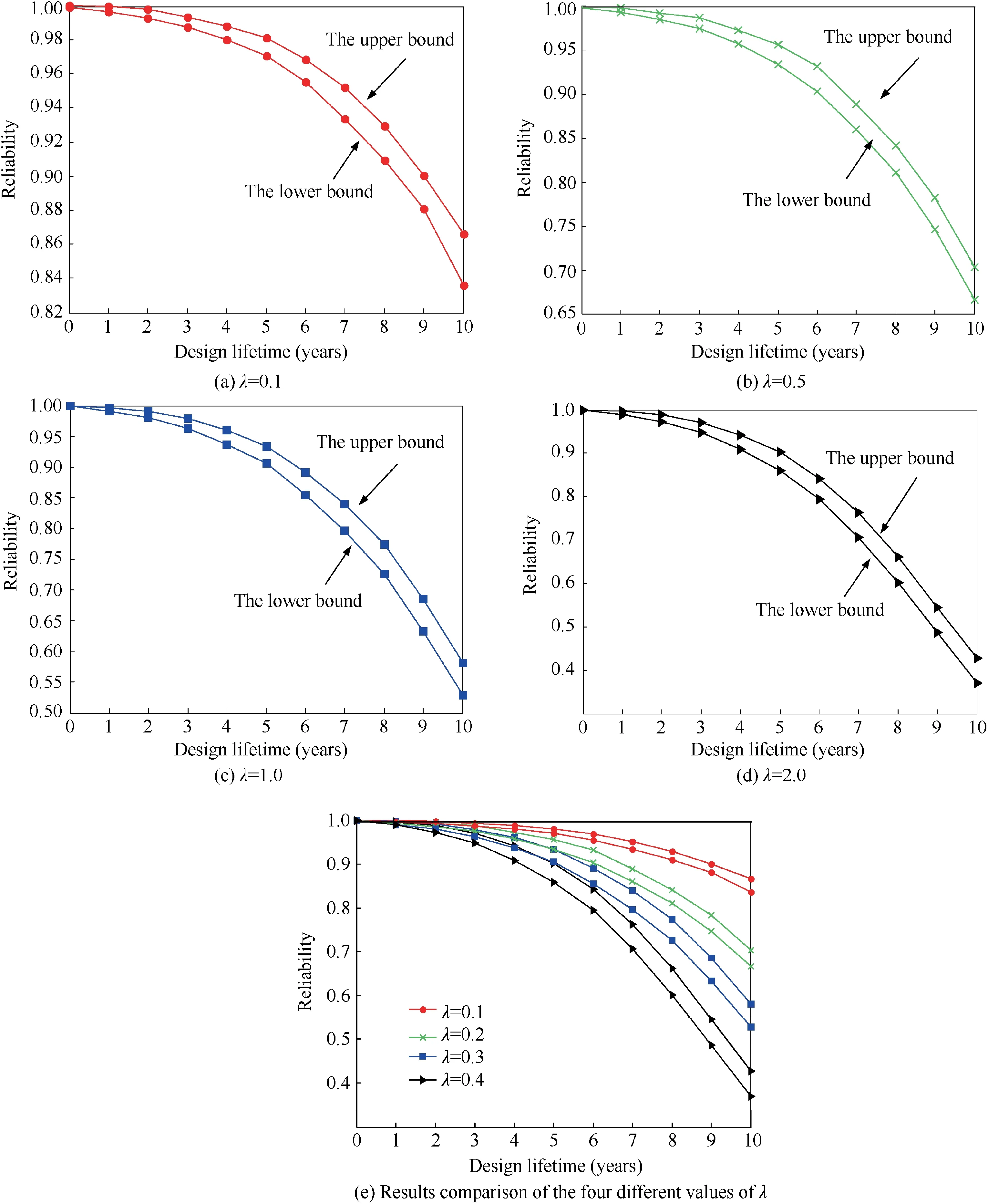
Fig. 7 Bounds of the reliability for the ten-bar truss structure over 0–10 years under different values of λ.

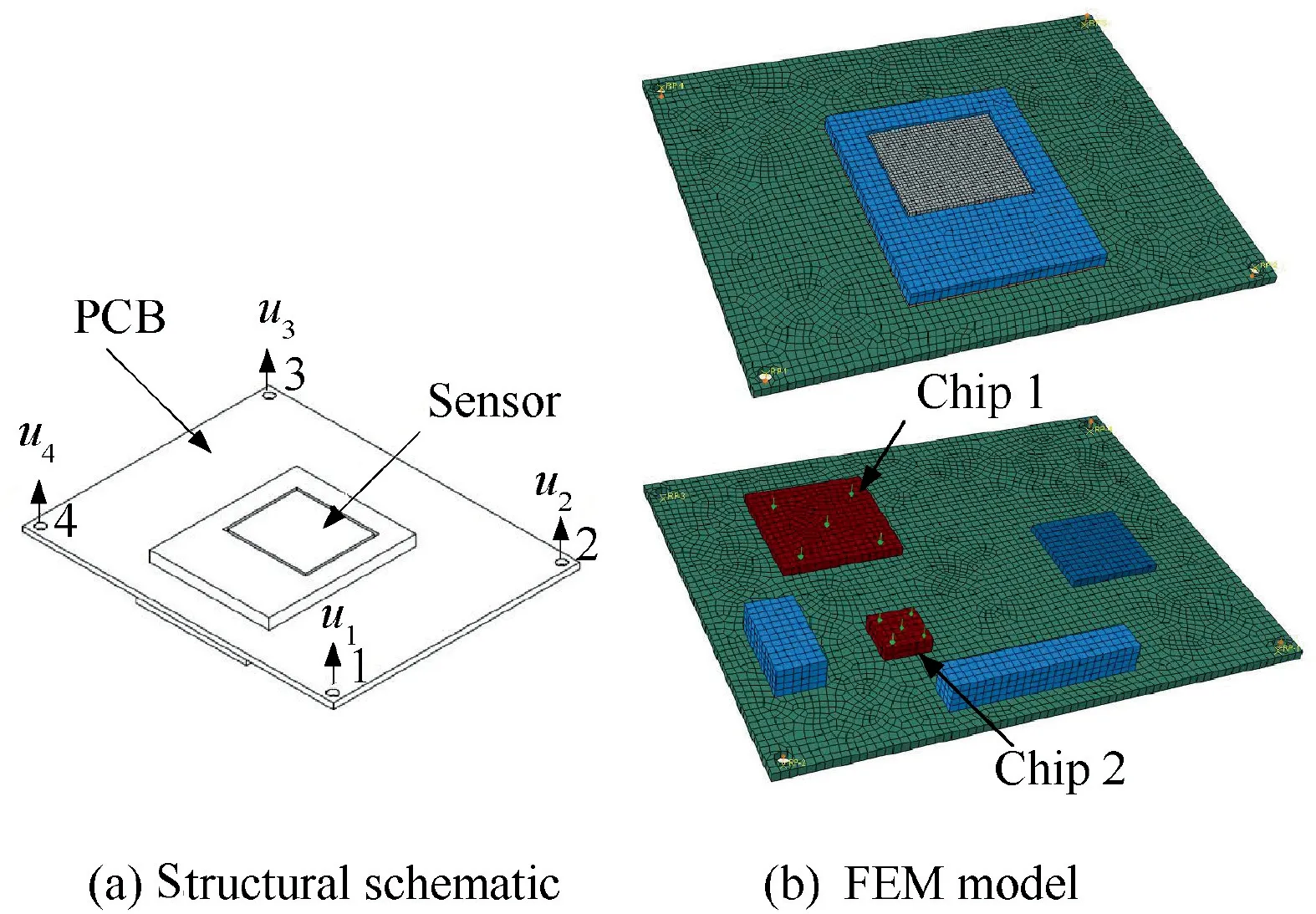
Fig. 8 A PCB module and its finite element model.71

5.3. A printed circuit board (PCB) module

Electronic equipment is extensively used in various productions， such as radar antenna and intelligent automobile. As an essential component of the electronic equipment， PCB has a remarkable influence on its service life and performance.Thus， it is necessary to conduct reliability analysis for PCB within its whole life. Fig. 8shows the PCB module of a high-definition camera. The function of its sensor is to collect optical signal， based on which the images can be formed. The location error of the sensor and thermal deformation affect the performance of the PCB module.The existence of the location error is primarily because of normal displacements in anchor points 1–4. The thermal deformation is mainly caused by the heat from chips 1 and 2.Table 2lists some material properties of the PCB module.

The maximum allowable normal deformation of the sensor is set as D＝0.3 mm，and D denotes the real maximum deformation， then the performance function for the PCB module is created as:

Using the proposed method with 10samples in its inner layer MCS and 5×10samples in its outer layer MCS， the lower and upper bounds of the reliability for the PCB module over 0–10 years are obtained， as shown in Table 4. It can be found that owing to the time-variant characteristic and the epistemic uncertainty in the power consumption of chip 1，the reliability of the PCB module is an interval within each design lifetime and both its lower and upper bounds decreasewith the design lifetime.The interval of the PCB module in the initial time is [0.998， 1]， indicating that the PCB module has a high initial reliability. Meanwhile， the width of interval of the reliability for the PCB module increases with the design lifetime. The width of interval of the reliability in the initial time is 0.002 while it increases to 0.02， 10 times of the initial value，slowly when the design lifetime is 10 years. Therefore， the dynamic aleatory and epistemic uncertainties should be considered simultaneously when performing time-variant time analysis for the lifecycle design of the PCB module.

Table 2 Material properties of the PCB module.71

Table 3 Distribution parameters of the uncertain parameters for the PCB module.

Table 4 Reliability of the PCB module over 0–10 years.

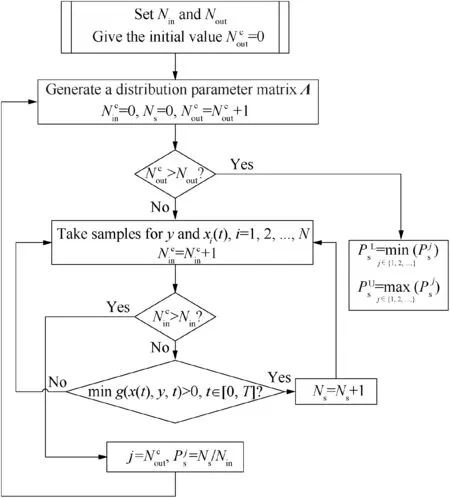
Fig. 9 Flowchart of the Monte Carlo simulation method for calculating the lower and upper bounds of time-variant reliability.

6. Conclusions

This paper proposes a novel imprecise stochastic process model for quantification of time-variant or dynamic uncertainty with insufficient experimental sample information in real-world problems. In the imprecise stochastic process model， the imprecise probabilistic model instead of a precise CDF is employed to characterize the parametric uncertainty at each time point for a time-variant parameter，which reduces the dependence on a large number of experimental samples.The auto-correlation coefficient function and the crosscorrelation coefficient function are defined to describe the correlation between variables at any two time points for imprecise stochastic processes. Compared with the traditional stochastic process model，the imprecise stochastic process model can handle the time-variant epistemic uncertainty and is expected to be a beneficial supplement for the former.For the convenience of analysis，taking the P-box model as an example，this paper also defines the P-box-based imprecise stochastic process and categorizes it into two classes，namely，the parameterized and nonparameterized ones. Further， the P-box-based imprecise stochastic process model is applied to time-variant reliability analysis and a Monte Carlo simulation-based method is proposed for calculating the interval of the dynamic reliability.As a novel model representing the time-variant epistemic uncertainty，the imprecise stochastic process remains to be further developed and improved in the future. Firstly， the more reasonable definitions for the auto-correlation coefficient function and the cross-correlation coefficient function can be proposed for the imprecise stochastic process model.Secondly，the imprecise stochastic process model can be constructed based on other various imprecise probabilistic models except for the P-box model. Thirdly， the imprecise stochastic process model can be applied to other important issues， such as the dynamics analysis and the dynamic reliability-based design optimization.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This work is supported by the Science Challenge Project，China(No. TZ2018007)， the National Science Fund for Distinguished Young Scholars，China (No. 51725502)， the Foundation for Innovative Research Groups of the National Natural Science Foundation of China(No. 51621004)， the Fundamental Research Foundation of China (No. JCKY2020110C105)，the National Natural Science Foundation of China (No.52105253).

Appendix. In order to obtain the lower and upper bounds of the reliability with the time interval ［0，T］， this paper proposes a two-layer Monte Carlo simulation method. The inner layer Monte Carlo simulation is used to calculate reliability under the given distribution parameters and called as the time

variant reliability analysis layer. The outer layer Monte Carlo simulation is used to find the lower bound and upper bound of the reliability and called as the optimization layer. Before the simulation analysis， the time interval ［0，T］ is discretized into Ntime points. The procedure of the two-layer Monte Carlo simulation method for calculating the lower bound and upper bound of the dynamic reliability is summarized here and the corresponding flowchart is given in Fig. 9.