降水信息空间插值模拟的不确定性分析

蒋好忱，雷宝佳，李昕

（1.自然资源部第一地形测量队，陕西 西安 710054；2.自然资源部第一地理信息制图院，陕西 西安 710054）

大气降水是水文循环最重要、最活跃的物理过程之一，存在较大的非线性和空间变异性。降水的空间变异是影响径流模拟、旱涝灾害预测管理以及其他水文问题的主要因素[1]。由于降水观测站点的布设有限以及影响降水空间分布的因素众多，因此很难准确获取某个区域的实际降水量的精确分布情况。空间插值是目前获取整个区域降水情况的主要方法[2]。空间插值方法很多，不同的插值方法结果差别很大，如何根据不同要素特点和区域特征选取最优的插值方法一直是地学研究的热点问题。

降水信息空间插值模拟的不确定性主要源于插值方法差异、站点数量变化、观测数据时间尺度、插值运算的空间尺度等方面。全面分析不确定性是实现区域降雨有效模拟的基础。国内外已有众多学者对降雨的插值方法进行了对比研究[2-11]，但大多只集中在不同插值方法本身的算法上，对其他影响插值模拟的不确定性因素考虑较少。本文以淮河流域为研究区，基于区域内170个雨量站的降雨观测数据，利用反距离加权法、克里金法等插值方法，通过比较平均绝对误差与平均相对误差，重点分析了插值方法差异、站点数量变化、像元尺度大小、时间尺度变化给降雨空间插值模拟带来的不确定性。

1 研究区概况与数据来源

本文选取淮河流域作为研究区，如图1所示。淮河流域地处我国南北气候过渡带，以北属暖温带区，以南属北亚热带区，气候温和。研究区最高气温为44.5℃，最低气温为-24.1℃，年均气温为14℃；年均降水量为920 mm，年均蒸发量为1 200 mm；汛期为6—9月。

图1 研究区域

分析数据来源于淮河流域170个雨量站2018年的观测资料，如图2所示。本文以该数据为基础，抽取并汇总了各站点2018年降雨总量和月降雨量。

图2 淮河流域雨量站分布情况

2 研究方法

本文主要从插值方法比较分析、站点数量变化分析、像元尺度变化分析、时间尺度变化分析4个方面对降水信息空间插值模拟的不确定性进行研究。从样区170个观测站点中随机选取21个站点作为误差检验站点，剩余的149个站点数据作为基础数据。插值结果生成后，将插值结果与实际观测值进行对比分析，计算不同条件下插值结果的平均绝对误差（MAE）和平均相对误差（MRE）的变化情况。

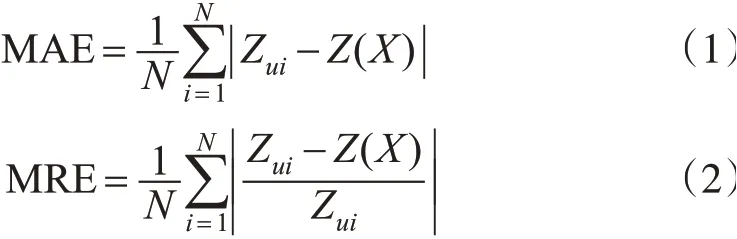
式中，Zui为第i个站点的实测观测值；Z(X)为估计值；N为检验站点数目。

在插值方法比较分析中采用反距离加权法、克里金法、样条函数法3种方法。为了保证插值结果的可比性，在站点数量变化分析、像元尺度变化分析、时间尺度变化分析中，均采用反距离加权法。站点数量变化分析分别随机选取149个雨量站中的80个、120个、149个站点进行年降雨总量的空间插值；像元尺度变化分析分别将像元大小设定为100 m、200 m、1 000 m进行年降雨总量的空间插值；时间尺度变化分析分别针对淮河流域2018年降雨总量以及7月与8月降雨量进行计算。

3 研究结果与分析

本文分别采用反距离加权法、克里金法和样条函数法对淮河流域2018年的年、月降雨量进行空间插值。3种插值方法得到的淮河流域降雨量如图3所示，可以看出，3种插值方法得到的降水空间变异性总体趋势为东南部降水多、西北部降水少，流域自东南向西北降雨量呈明显的递减趋势。

图3 3种方法淮河流域年降雨量插值结果

不同插值方法的误差统计与分析如图4、表1所示，可以看出，不同的插值方法具有明显的精度差异，其中克里金插值方法精度最高，全年MAE为23.38 mm，MRE为8.18%；样条函数法精度最低，全年MAE为34.91 mm，MRE为12.4%。

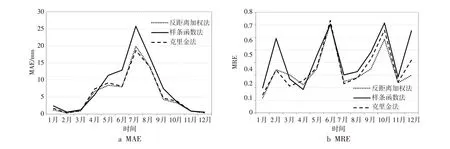
图4 插值方法误差统计

表1 不同插值方法插值结果的误差统计

本文分别利用80个、120个、149个站点数据，采用反距离加权法对流域年降雨总量进行空间插值，并与21个检测点数据进行对比分析，结果如表2所示，可以看出，随着插值点数量的增加，MRE越来越小，表明插值站点数目越多，插值结果越接近实际观测值。

表2 不同站点数量插值结果的误差统计

本文基于149个站点数据，采用反距离加权法分别按100 m、200 m、1 000 m像元大小进行空间插值，并对精度进行统计，结果如表3所示，可以看出，像元大小由100 m到1 000 m的变化过程中，误差存在一定的变化，但幅度不大，表明在一般分辨率水平下，像元大小对插值结果的不确定性具有一定影响，但影响远小于插值站点数量。

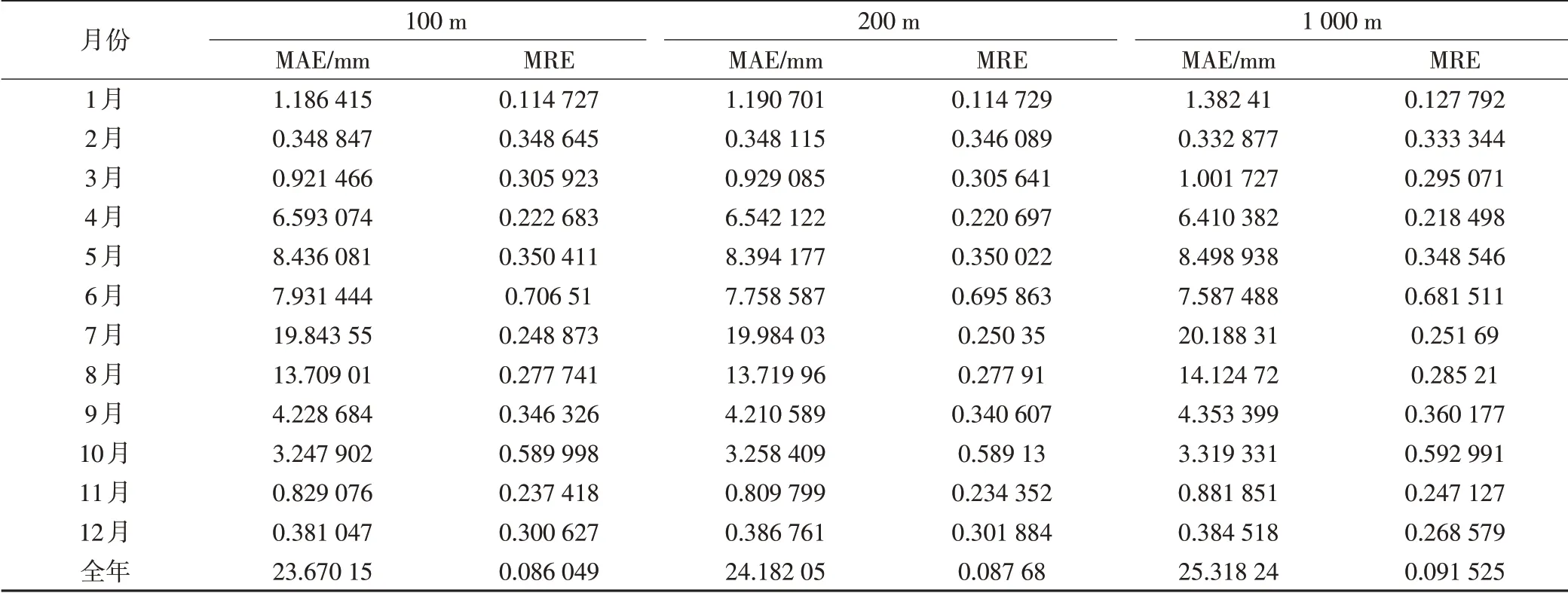
表3 不同像元尺度插值结果的误差统计

本文利用反距离加权法分别对149个站点年、月降雨数据进行空间插值，并对插值结果进行误差统计，结果如表4所示。由于不同时间尺度降雨观测值不同，MAE缺乏可比性，因此只考虑MRE的变化情况。之所以选择7月、8月的降雨量，是因为这两个月的降雨量较集中，可避免因无降雨而反映不出降雨的空间变异。结果表明，在时间尺度由月到年的变化过程中，降雨信息的精度变化极大。在年降雨插值中，MRE只有8.49%，而相同插值方法、相同站点数量插值得到的7月和8月MRE则达到了24.92%和28.10%以上的水平，说明时间尺度越小，插值结果的不确定性越大，常规插值方法很难保证该时间尺度插值结果的精度。

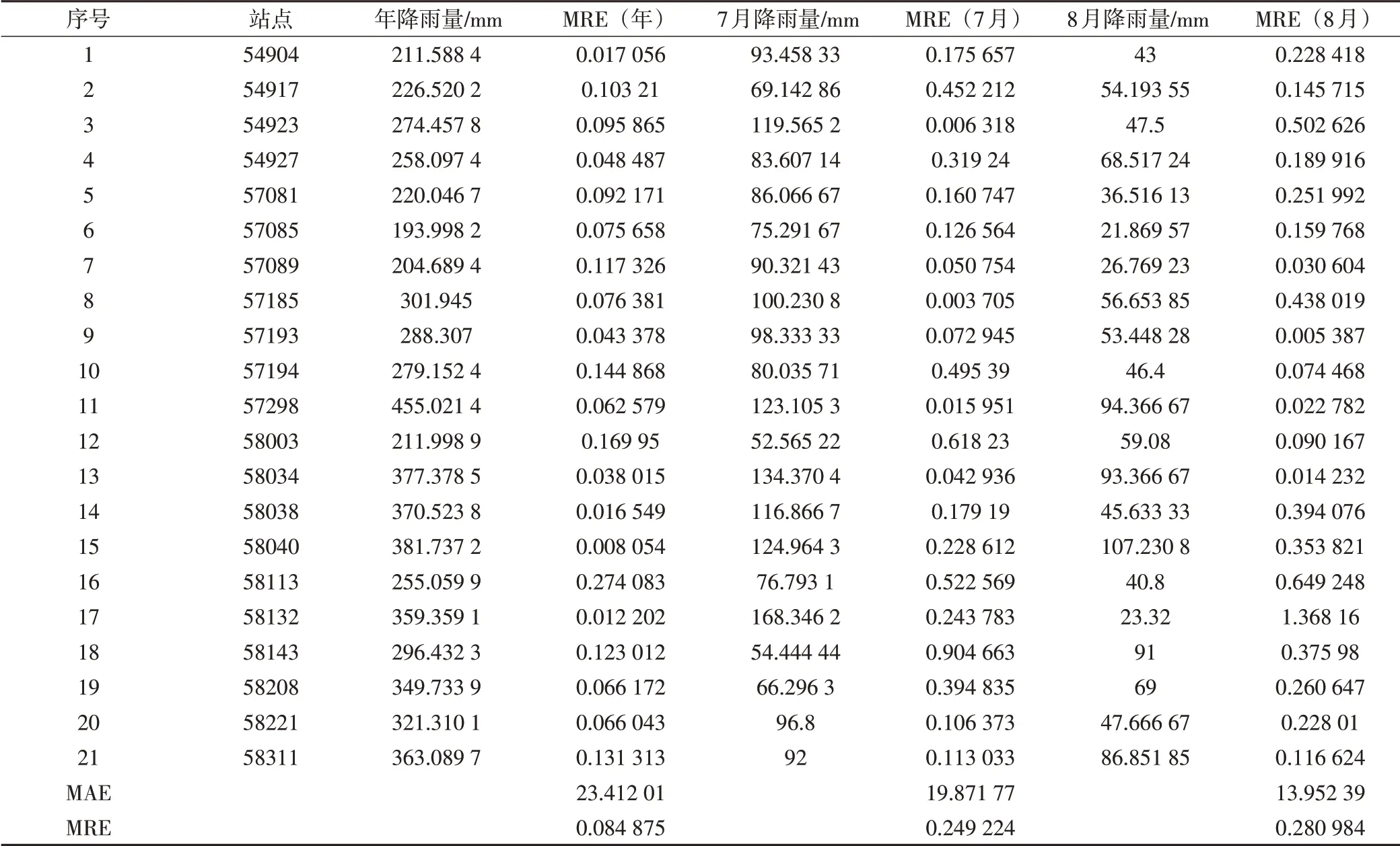
表4不同时间尺度插值结果的误差统计

4 结语

本文通过对淮河流域2018年降雨信息进行空间插值比较分析发现：①不同空间插值方法插值结果的精度有较大差异，是降水不确定性的主要影响因素；②站点数量越多，插值精确度越高；③像元尺度变化对降水插值结果的不确定性只有微弱影响；④时间尺度越小，插值结果的不确定性越大，常规插值方法很难保证该时间尺度插值结果的精度。

需注意的是，像元尺度变化并不能等同于空间尺度变化，空间尺度通常还包含空间范围的变化。在空间插值研究中，空间范围变化往往带来插值站点数量的增加或减少，因此空间范围变化带来的插值结果的不确定性实际上既包括了像元尺度，也叠加了站点数量变化带来的不确定性，易造成混乱。本文将站点数量变化与像元尺度变化分开单独考虑，在一定程度上应更具合理性。