深度学习密集匹配中样本精度与匹配精度的关系研究

李志勇，官恺*，牛泽璇，晏非，孙曼，闫兆婵

（1.61363部队，陕西 西安 710054）

密集匹配在三维重建[1]、汽车驾驶[2]和航空摄影测量[3-4]等众多领域都有重要应用。其核心是在含有重叠区域的两幅图像上依据特征为每个像素寻找同名点，其精度将直接影响实际应用中的测量精度。密集匹配的发展经历了漫长的过程，SAD、SSD[5]、模拟退火[6]、动态规划等传统方法是依据人工设计的特征描述符寻找同名点，因此提取特征需要较强的专业背景知识，通常鲁棒性较差且精度有限。随着计算机硬件的发展和深度学习理论层面的逐渐完善，深度学习在短短几年时间获得了较大的发展。MC-CNN[7]网络首次利用深度卷积网络自动提取密集匹配所需特征，发挥了深度学习基于数据驱动提取特征的优势，选择出鲁棒性更强的特征；DispNet[8]在光流网络FlowNet[9]的基础上改进了上采样部分，应用于密集匹配，取得了不错的效果；iResNet[10]引入了多尺度信息提取模块和贝叶斯精化视差模块，进一步提升了匹配精度；GCNet[11]摒弃了通用的全卷积网络，在网络结构中引入了视差代价构建模块，并采用三维卷积的方式计算匹配代价，利用视差软回归将分类问题变为回归问题；但由于GCNet缺少了多尺度信息，在大面积平滑区域表现欠佳，因此PSMNet[12]在其基础上增加了金字塔池化模块，以增加全局特征克服弱纹理和无纹理区域带来的影响，同时在匹配代价构建部分采用了堆叠沙漏模块，使不同位置的特征可以相互参考空间位置，进一步提升网络精度。后期的大部分网络均以PSMNet为基础，如增加了分组相关的GwcNet[13]以及利用视差唯一性的AcfNet[14]；参考文献[15]进一步借鉴传统匹配思想，利用影像金字塔和迭代的方式，将视差范围由粗到精，逐步迭代，取得了不错的效果。

虽然监督密集匹配网络在性能上已接近甚至超过传统方法[16]，但监督网络本质是对匹配过程的一个高维拟合，需以样本数据为基准训练拟合参数，因此样本的精度对于监督网络匹配效果十分重要。当前监督网络所采用的数据集样本精度极高，如Scene Flow[8]虚拟场景数据集的样本数据是通过计算机精确计算得到的；KITTI数据集采用激光雷达，且经过人工修正，整体精度可信度较高。然而，航空数据集样本标注存在困难，且真实样本数据在制作过程中存在一定的误差，因此需要考虑样本数据误差对密集匹配精度的影响，并进行进一步分析，以掌握其规律。

1 深度学习方法

1.1 密集匹配网络结构

深度学习密集匹配端到端常见的网络结构包括DispNet、GCNet和PSMNet等。

1.1.1 DispNet

DispNet网络基于FlowNet改进，网络架构为通用全卷积网络，整个网络类似于U-Net[17]，分为特征提取端和分辨率恢复端，通过跳层连接，包括DispNetS和DispNetC两个版本，前者结构如图1a所示，经过特征提取和分辨率恢复直接得到视差图，后者特征提取端前3层为孪生网络，且在融合时额外加入了相关信息，融合后的操作与前者一致，即通过卷积层继续进行更高级别的特征提取以恢复分辨率，生成视差图，结构如图1b所示。

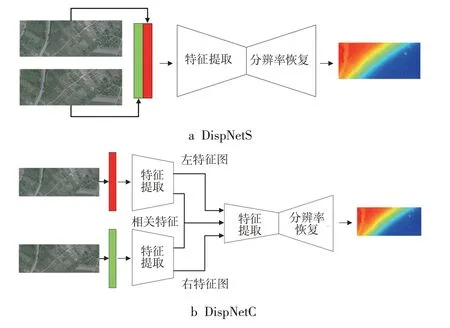
图1 DispNet结构图

1.1.2 GCNet

GCNet为端到端深度学习架构，与通用的全卷积网络设计思想不同，其设计更有利于密集匹配，设计的匹配代价构建、匹配代价计算以及视差软回归等模块的改进版一直沿用至今，效果显著优于通用全卷积网络结构。其流程包括特征提取、匹配代价张量构建、匹配代价计算和视差软回归。该网络中的特征提取部分增加了多个残差块，提取特征能力更强；匹配代价通过叠加不同偏移的左右特征图的组合构建；构建的匹配代价经过三维卷积模块计算左右特征图相应偏移的匹配代价；视差软回归将匹配代价的分类问题转为回归问题，形成最终视差结果。GCNet的网络结构如图2所示。

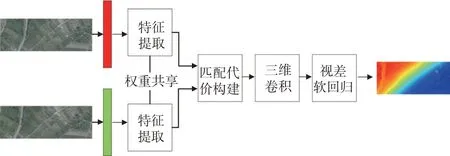
图2 GCNet结构图

1.1.3 PSMNet

PSMNet沿用GCNet的架构，包括特征提取、金字塔池化、匹配代价构建、匹配代价计算以及视差回归5个部分。改进的核心思想是在GCNet的基础上引入多尺度信息，具体体现在特征提取段追加扩张卷积残差块、金字塔池化和堆叠沙漏3个部分，进一步提升网络的精度和鲁棒性。其结构如图3所示。PSMNetB和PSMNetS为PSMNet网络的两个版本，PSMNetB在代价匹配部分采用常规三维卷积加跳层的方式，而PSMNetS采用堆叠沙漏方式。

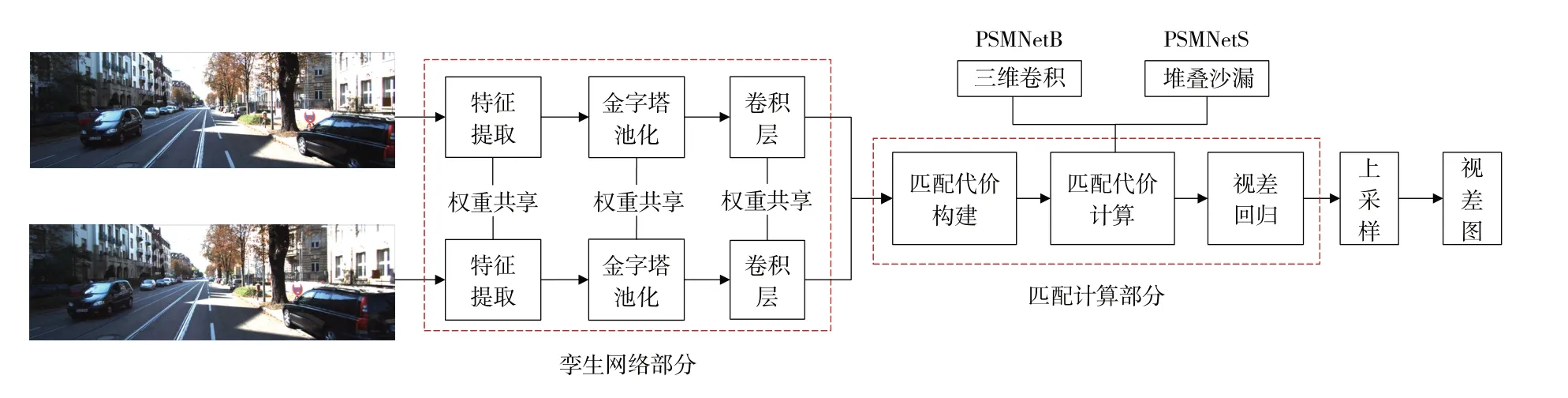
图3 PSMNet结构图

1.2 迁移学习

迁移学习是将已训练好的模型应用于其他数据集的策略。该方法利用了原有模型的泛化性能，若能在新数据集上产生更好的效果，则可节省大量运算时间。迁移学习包括直推式迁移和模型微调两种方式，前者对已训练好的模型不作任何调整，直接应用于新数据集；后者则对新数据集进行微调，使得模型更适合于该数据集。模型微调又分为整体微调和部分层微调，本次实验采用模型微调中的整体微调。

2 数据集概况

为全面分析深度学习中数据集样本精度与密集匹配精度的关系，实验共涉及Scene Flow、KITTI2012[18]，KITTI2015[19]、Vaihingen[16]和WHU[20]等5个数据集，其中Scene Flow数据集作为预训练数据集，其余4个数据集作为测试数据集。

2.1 Scene Flow数据集

Scene Flow数据集出自于DispNet，为虚拟场景，通过虚拟场景三维投影到二维的方式获得样本数据。由于该过程由数学公式直接计算得到，因此相较于真实场景数据集，该数据集样本数据精度极高，更适合作为迁移学习中的预训练数据集。该数据集分为FlyingThings3D、Driving、Monkaa，训练集包括35 858对图像，测试集包括4 370对图像，图像尺寸为960像素×540像素。

2.2 KITTI数据集

KITTI数据集为汽车驾驶的真实场景，包括KITTI2012和KITTI2015两个子集，视差图由激光雷达测距反算得到，为半稠密视差图，为保证样本标注精度，该样本经过人工修正。KITTI2012的训练集和测试集分别为194对和195对图像，图像尺寸为1 226像素×370像素；KITTI2015的训练集和测试集均为200对图像，图像尺寸为1 242像素×375像素。

2.3 Vaihingen数据集

Vaihingen数据集为德国航拍场景，由3条航带26张乡村影像组成，图像尺寸为9 240像素×14 430像素，航向和旁向重叠度均为60%。经过裁剪整理共包括731对图像，尺寸为955像素×360像素，训练数据和测试数据的比例为8∶2，样本数据由7款商业软件匹配的DSM取平均值反算得到。整个区域地形相对平坦，包括低矮的房屋群、河流、树林和农田等。

2.4 WHU数据集

WHU数据集为贵州乡村航拍场景，飞行平台为无人机，拍摄高度约为550 m，分辨率为10 cm，航向和旁向重叠度分别为90%和80%。经整理和裁切共包括10 979对图像，其中8 316对用于训练，2 663对用于测试，尺寸为768像素×384像素。场景为部分高层建筑、少量工厂以及一些山脉河流。

3 实验结果与分析

实验在Windows10操作系统下开展，采用Anconada虚拟环境，基于PyTorch框架，语言为Python，显卡为NVIDIA GTX 1080Ti，显存为11G。batchsize通过梯度累加模拟实现，设置为8，优化其采用Adam，参数分别为β1=0.9，β2=0.999。训练过程中图像会被随机裁剪为512像素×256像素，一方面增加训练速度，另一方面做数据增强。参数指标采用终点误差（EPE）和3像素误差（3 PE），其中EPE为预测视差与真实视差之间绝对值的平均值，单位为像素；3PE为EPE大于3像素占总点数的百分比，单位为百分比。

实验最大视差设置为192像素。首先将Sence Flow数据集作为迁移学习预训练数据集，预训练10轮；然后在其余4个数据集上进行微调和测试，其中在KITTI数据集上训练1 000轮，在Vaihingen数据集上训练300轮，在WHU数据集上训练30轮。作为对比，采用未经迁移学习的数据进行测试，由于未经迁移学习的模型收敛速度相对较慢，在KITTI数据集上训练2 000轮，在Vaihingen数据集上训练600轮，在WHU数据集上训练60轮。按照国家《测量误差及数据处理》技术规范，实际数据中所包含的误差可分为系统误差、随机误差和粗大误差[21]，为更贴近真实场景，探究样本误差与预测误差的关系，本文分别对3种误差进行模拟实验。

3.1 实验网络选择

本次实验的主要目的是分析数据样本精度与密集匹配精度之间关系，需要大量消融实验，因此运算时间将作为选取的重要依据。由于数据集图像大小数量各异，因此统一在KITTI2015数据集上进行测试，根据测试结果列出各网络运行2 000轮所需时间，同时依据本文公开展示精度列出各网络精度，如表1所示，其中训练1次是指单幅图像裁切为256像素×512像素从输入到反向传播完成的时间，测试1次是指单幅完整图像生成视差图所需时间，累计总耗时为训练时间与测试时间的总和，可以看出，DispNet两个版本的网络累计耗时远低于其他网络，且时间相差较小；DispNetC的精度高于DispNetS，因此综合考虑精度和运行时间，本文选取DispNetC作为实验网络。

表1 各网络运行时间与网络精度

3.2 样本系统误差与精度的关系

系统误差是指由系统本身造成的误差，通常分为恒定误差和按照一定规律变化的变化误差。恒定误差的绝对值和符号保持恒定，在实验中通过对所有像素增加或减少相同的像素偏移值进行模拟；变化误差规律种类较多，通常误差值以一定规律随测量条件变化而变化，实验采用统一百分比缩放的方式进行模拟，即误差随视差值实际大小变化而变化，视差值越大，则误差越大，反之则越小。系统恒定误差模拟结果如表2所示，可以看出，深度学习方法具有一定的容错能力，理论上来说，系统偏差N像素，预测偏差应相应偏移N像素，而实际效果却是在迁移学习条件下，系统偏差新增1像素，实际偏差仅平均增长0.47像素，虽然随着系统偏移距离的增加，误差增幅也在加速增加，但在一定范围内，网络仍具有较强的容错能力，尤其在1像素内，预测误差增幅远小于系统固定误差。

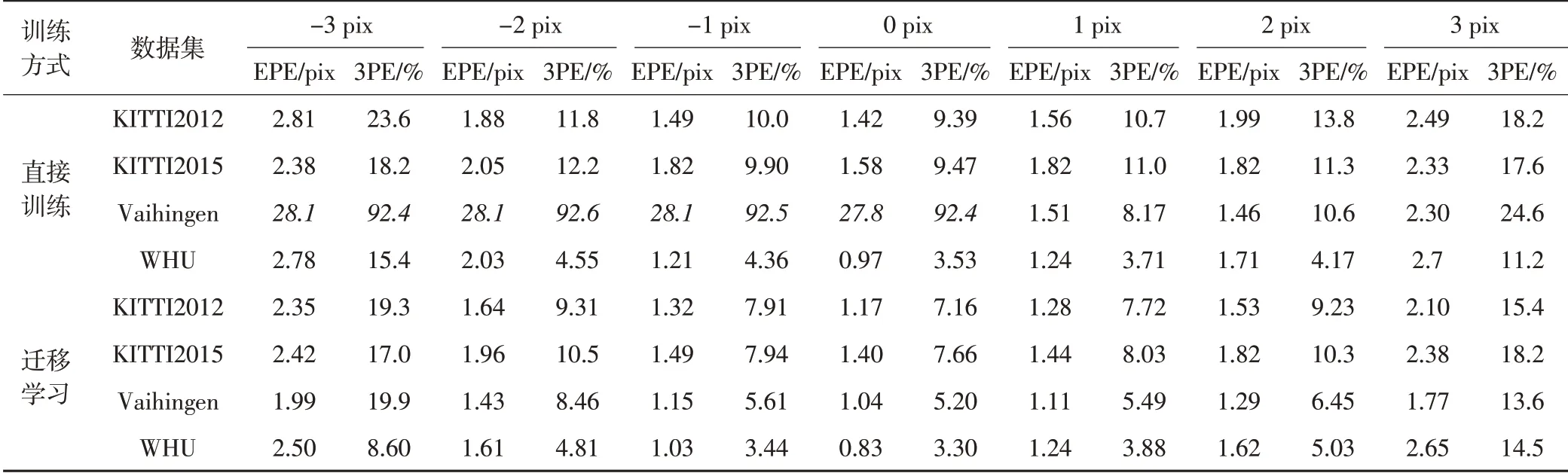
表2系统恒定误差随偏移距离变化

在迁移学习方面，对比迁移学习和直接训练0像素偏移列可知，迁移学习方法可提升网络的精度，直接训练网络模型虽然训练的轮次为迁移训练网络模型的两倍，但整体精度较低；相较于直接训练，迁移学习方法在KITTI2012、KITTI2015和WHU三个数据集上的EPE分别降低了0.25像素、0.18像素和0.14像素，3PE分别减少了17.6%，13.9%和14.4%，平均减少15.3%。

从抗噪角度来看，迁移学习模型预测误差随系统误差增加的幅度更小，从而说明迁移学习在加速收敛，节约时间的同时还能提升精度。对直接训练和迁移学习所有EPE结果分别求和，考虑到Vaihingen数据集上直接训练模型表现异常（斜体处不收敛），不参与计算。最终，直接训练模型的EPE偏移总和为39.08像素，而迁移学习模型的EPE偏移总和为35.78像素，因此迁移学习模型整体的鲁棒性优于直接训练模型。另外，通过比较Vaihingen数据集迁移学习和直接训练方法可知，不收敛的网络经过迁移学习，可稳定收敛，进一步印证了迁移学习方法可提升网络的鲁棒性的结论。

进一步探究Vaihingen数据集不收敛原因，通过其他3个数据集收敛以及Vaihingen数据集上预训练后网络仍可收敛，排除网络本身问题；因此该问题可能是由过拟合或数据样本自身精度引起的。过拟合的典型表现为在训练集上表现良好，在测试集上表现极差。因此，本文通过该方法判断是否为过拟合，将训练和测试结果分别制作EPE曲线，如图4所示，可以看出，无论是在训练集还是在测试集，EPE均在26～30像素之间，说明不是过拟合问题，因此可能为数据集标签精度问题。

图4 Vaihingen数据集EPE曲线

由于该数据集标签数据是由7款商业软件匹配的DSM反算得到的，无论是匹配点本身还是计算过程中都可能引入误差、降低数据集精度，使网络无法通过监督方法学习到匹配的本质。为验证猜想，本文采用无监督的方法[22]进行实验，结果如表3所示，可以看出，网络可收敛，说明标签精度确实存在问题。另外，以Vaihingen数据集标签加1像素的结果为训练标签进行实验发现，网络可以收敛；且迁移学习结果中，标签加1像素作为标准数据的训练结果明显低于标签减1像素的结果，说明原数据集存在1像素的系统偏差，整体结果偏大。

表3 无监督方法结果

通过进一步分析发现，Vaihingen数据集和WHU数据集都属于遥感数据集，但直接训练方法在WHU数据进行1像素的偏移后仍可收敛，这与Vaihingen数据集存在1像素系统偏差的结论矛盾。为了探究该问题，需从数据集图像纹理特征和视差图分布进行分析，本文做了相关工作，绘制了各数据集的视差分布图，如图5所示，可以看出，Vaihingen数据集的差异主要体现在视差分布上，其视差分布更离散，其他数据集视差值均集中在0～100像素内，而Vaihingen数据集有大量点的视差值在100像素以上。

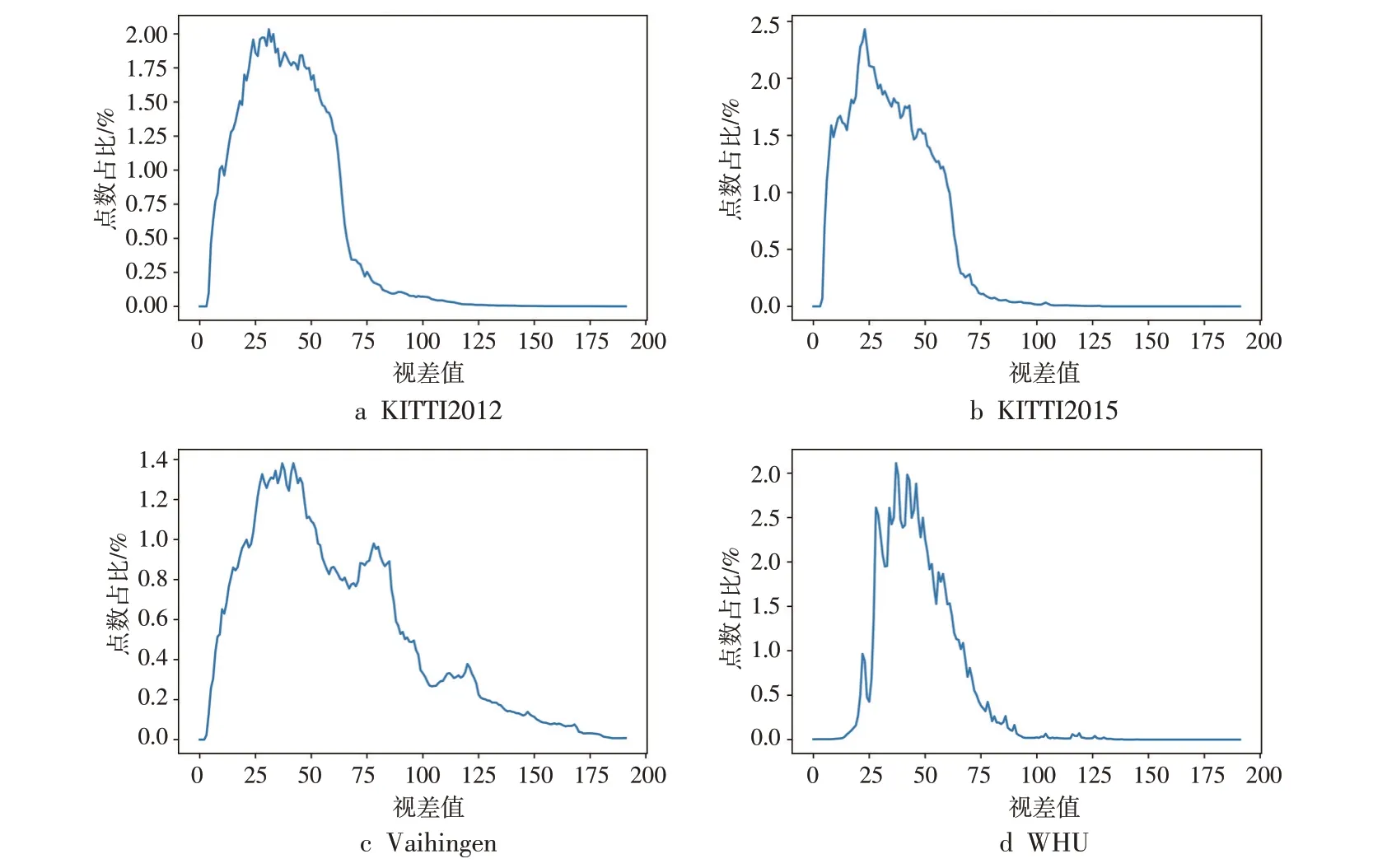
图5 各数据集视差分布

此外，对比两个数据集的规模发现，Vaihingen数据集的图像数量仅为WHU数据集的1/10，由此可推断在视差分布范围大且数据集标签较少的情况下，直接训练方法难以收敛。解决办法是先在Scene Flow数据集上构建预训练模型，再利用迁移学习方法，则可得到较稳定的结果。由于直接训练方法导致网络不稳定，且整体精度较差，后续精度实验均采用迁移学习方法。

变化系统误差模拟常见的误差随视差值增大和减小的情况，通过将全图视差值乘以固定的比例系数进行模拟，范围为70%～130%，结果如表4所示，可以看出，样本数据经过等比例变化后，误差精度下降速度远超系统固定误差，即使偏差约为10%，也会产生巨大误差。进一步分析原因可知，与恒定误差不同，等比例误差与视差值本身有关，本文计算得到KITTI2012、KITTI2015、Vaihingen和WHU数据集的视差均值分别为39.04像素、34.21像素、59.85像素和46.99像素，10%均超过了3像素。对比表2中±2像素、±3像素偏移和表4中90%、110%发现，二者接近，由此可推断该类误差与视差值本身相关。实际匹配过程中，视差值通常较大，导致误差整体较大，因此对于该类误差，在实际测量中需要避免。

表4 等比例误差和预测精度关系

3.3 样本随机误差与精度的关系

在真实场景中，随机误差是不可避免的。通常随机误差具有一定的规律性，即单峰性、对称性、抵偿性和有界性，一般呈正态分布。因此，在实验中通过对原始数据增加一个正态分布的噪声，模拟随机噪声，分别探究样本数据噪声均值和噪声标准差对匹配精度的影响。在研究噪声均值的影响实验中，噪声标准差统一为3像素，均值从-3～3像素进行实验。噪声均值和预测精度关系如表5所示，可以看出，随着误差均值的增加，预测误差增幅迅速增加，说明随机误差中的均值误差对预测误差影响较大。对比表2和表5相同行数据发现，整体误差在数值和变化规律上均较接近，说明无论误差是否随机，样本数据均值的偏移都会对匹配精度产生相近的影响。此外，表2和表5中0像素偏移列，在均值为0像素，标准差为3像素的情况下，各数据集均未产生较大偏差，说明在一定标准差范围内，随机误差对预测精度影响较小。

表5 噪声均值偏差与预测精度的关系

为验证噪声标准差对网络的影响，将噪声均值设置为0，标准差从0～6依次进行实验，结果如表6所示，可以看出，在噪声均值不变的情况下，随着噪声标准差的增加，整体上EPE和3PE并没有明显增加，进一步印证了一定范围内的随机噪声对精度影响较小的结论。

表6 噪声标准差与预测精度的关系

3.4 样本粗大误差与精度的关系

在实际测量中，粗差或多或少存在，其结果可能对整体测量结果产生严重影响，因此需要对其影响进行分析。实验通过在0～12%比例范围增加20像素的方式模拟粗差，结果如表7所示，可以看出，随着样本数据粗大误差比例的增加，EPE和3PE未出现明显增加，说明网络对于数据样本的少量粗大误差具有一定的“过滤”效果，使得网络在样本数据少量偏差的情况下，仍能保持网络精度；此外，部分数据在增加少量粗大误差时，效果甚至更优，相当于给原有的集合增加了“噪声”，训练这样的数据集有助于增加模型的鲁棒性，效果类似于“数据增强”。

表7 粗大误差与预测精度的关系

综合上述3种误差发现，无论是随机误差还是系统误差，整体性的均值偏移均会使密集匹配精度下降，且随着偏移距离的增加，误差增幅也在增加；而随机性偏移在保证均值无偏移的前提下，在一定范围内精度并没有明显下降，甚至还有小幅度提升；此外，基于视差本身的百分比误差与该区域视差值本身相关，通常对深度学习网络训练是“灾难性”的，微小的百分比偏差，将引起最终匹配上巨大的误差。

4 结语

本文在多个数据集上分别模拟了含有系统误差、随机误差和粗大误差的样本数据，并进行了测试分析。实验首先验证了迁移学习方法对网络收敛速度、鲁棒性的帮助，能在减少训练时间的同时增加密集匹配精度，平均误差减少了15.3%，并通过进一步分析Vaihingen与WHU数据集的差异发现，环境复杂且数据样本较少的数据集在含有系统误差时更容易不收敛，可通过迁移学习方法解决该问题；其次证明了深度学习方法在一定范围内具有较强的容错性，但在超出该范围后误差增幅逐渐变大；最后说明了深度学习方法的抗噪性能主要体现在对抗随机误差，少量的随机误差甚至会使匹配精度有一定提升，而系统性的整体偏差对精度影响较大，尤其是百分比误差，对匹配精度影响巨大。本文也存在一些局限性，如未指出随机粗差使网络发散的边界条件，后期将进行进一步研究。