剖析初中数学图形旋转问题的几种方法
田佩佩
(泰州市胡庄初级中学,江苏泰州,225300)
图形旋转问题一直是初中数学课程教学的重要内容,也一直是困扰多数学生的难题,特别是图形旋转后位置的确定问题,使得不少学生陷入困境.在图形旋转问题的教学中,不少教师乐于绘图软件直接旋转获得最终图形,无形中降低学生的作图要求;不少学生总是采取“猜测”的方法来绘制旋转后的草图,但是对“猜测”结果图形中各个表征量之间的关系总是难以把握,一度使得难题无法解决,这是初中数学“图形旋转问题”中的一种常态现象,本文基于这种现状,从图形旋转的实质视角出发,借助于典型案例,探讨解决图形旋转问题的具体方法,希望能给教育同仁带来一些帮助和参照.
1 图形旋转问题的本质呈现
在某一平面内△ABC绕着其外部一点O逆时针旋转θ角度后记为△A′B′C′,此旋转过程的本质可以看成:A、B、C均以O点为圆心同时逆时针旋转θ角度后连接三点构成三角形△A′B′C′,如图1所示,则该图形旋转问题中存在的规律如下:
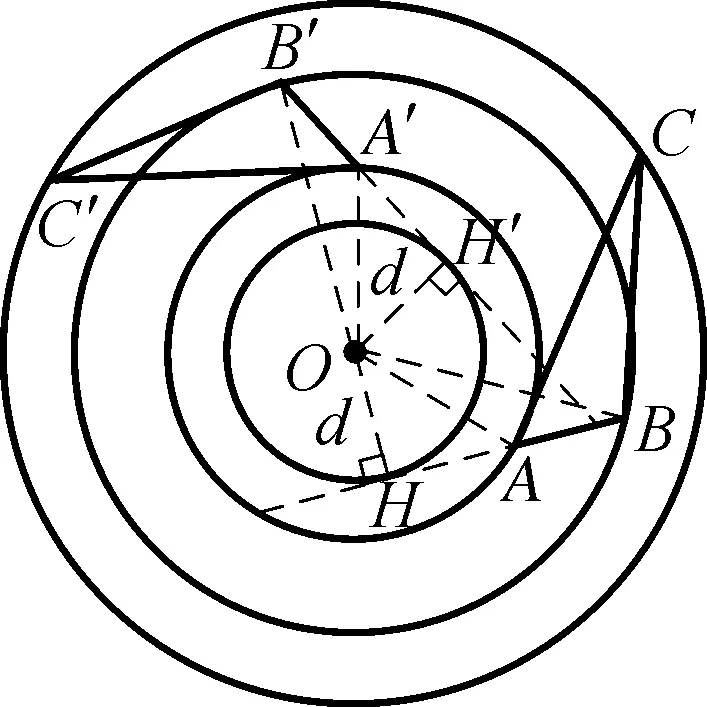
图1
规律1:旋转前后相关点与中心之间的距离相等.(OA=OA′、OB=OB′、OC=OC′)
规律2:旋转过程中各个对应点与中心连线的角度均等于旋转角度θ(∠AOA′=∠BOB′=∠COC′=θ)
规律3:旋转前后三角形的三条对应边长和角度相等.(AB=A′B′、BC=B′C′、AC=A′C′、∠A=∠A′、∠B=∠B′、∠C=∠C′)
规律4:旋转过程遵循可逆性特征,△ABC以O点为中心逆时针旋转θ变为△A′B′C′,同样△A′B′C′以O点为中心顺时针旋转θ变为△ABC.
规律5:旋转前后中心点O至对应线段之间的距离相等为d,三角形对应边与以O点为圆心,d为半径的圆相切.
证明:根据图形旋转的规律可知,OA=OA′,OB=OB′,AB=A′B′则△AOB≌△A′OB′即∠OBA=∠OB′A′,在直角△BOH和△B′OH′中,OB=OB′、∠OBH=∠OB′H′、∠OHB=∠OH′B′则△BOH≌△B′OH′即OH=OH′.
数学教师引导学生分析图形旋转问题中的规律时,学生在与教师互动的过程中进一步认识到旋转图形的本质规律,有助于学生主动分析问题、探究解决问题的思路与方法,进而不断积累解题经验与技巧,真正理解图形旋转问题的规律和本质.
2 多元视角破解图形旋转难题
例题1如图2所示的等腰△ABC中,AB=AC=5,BC=8,现将△ABC以C点为中心旋转一定角度,△ABC中A、B两点旋转后分别记为A′和B′,其中,点B′在线段AA′的延长线上,试求线段AA′的长度.
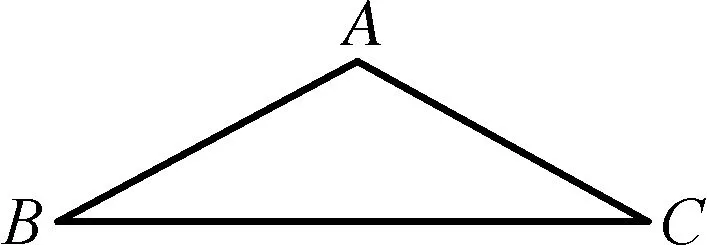
图2
剖析:本题中△ABC以C点为中心旋转一定角度后,学生无法直接确定A′和B′的位置,根据题意可知,B′点与A和A′三点共线,图形旋转中无法直接确定旋转后的图形位置,数学教师可以引导学生借助于草图的绘制探寻各个量之间的关系,最终找到解决问题的方法.
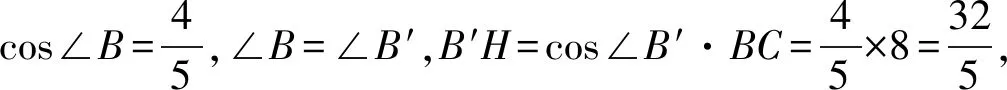
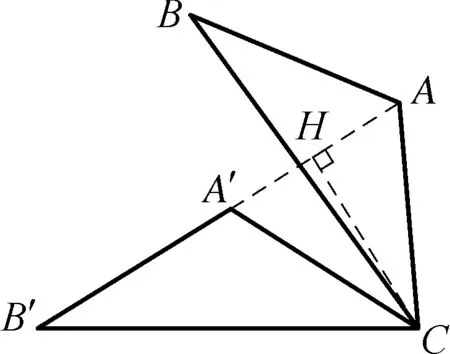
图3
点评:图形旋转问题一直是初中学生数学学习的难点,主要是学生难以理解旋转前后各个量之间的确定关系.从教学实践来看,引导学生正确地画出运动草图,可以帮助学生洞悉旋转过程中的规律与特征,有助于图形旋转难题的解决.
解法2根据图形旋转规律可知,旋转图形△ABC在绕C点旋转的过程中,直线AB与C点之间的垂直距离为定值,如图4所示,过旋转中心点C作CD⊥BA交BA延长线于D点,△ABC在旋转过程中BD始终与以C点为圆心、CD长度为半径的圆相切;显然,题设中“B′点与A和A′三点共线”可以理解为“圆C的切线恰好过点A”,过点A作出圆C的切线AD′(其中点D′为切点),根据图形旋转规律可知旋转过程中对应线段长度保持不变,在AD′的延长线上确定A′和B′,使得A′D′=AD、A′B′=AB,连接B′C、A′C,则△A′B′C为△ABC绕C旋转后的精确图形.
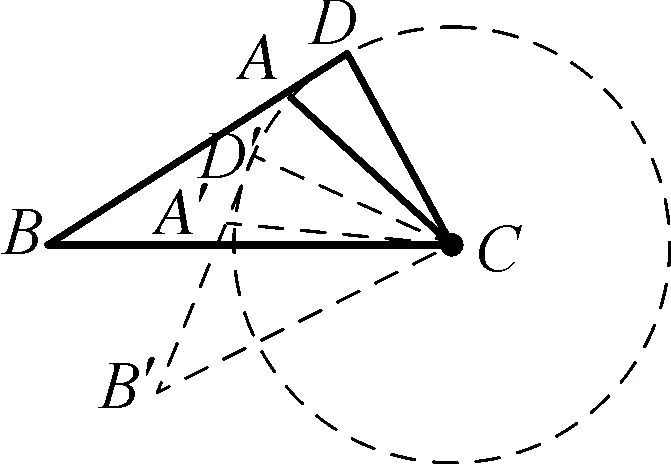
图4
点评:利用图形旋转规律和本质,打破采取“作草图”的方式获得更加精确的图形,在实际教学过程中,此种解法容易让学生理解旋转过程中的本质规律的应用,进而提升解题效率.
解法3根据图形旋转规律可知,图形旋转前后的位置都是固定的,由图形旋转之前位置绘制出旋转之后的位置,显然也可以利用“旋转可逆”的性质特点,由图形旋转之后的位置来绘制出旋转之前的位置,本题中可以将旋转前后端位置状态进行对调,题设中△ABC可以看成旋转之后的位置状态而修改为△A′B′C,根据题设信息可知,A、A′、B′三点共线,CA=CA′,现以C点为圆心,CA′长度为半径作圆交B′A′的延长线于A点,现以点C为圆心CB′长度为半径作圆、以A为圆心A′B′长度为半径作圆,两个圆弧相交于B点,如图5所示,则旋转之前的图形为△ABC.
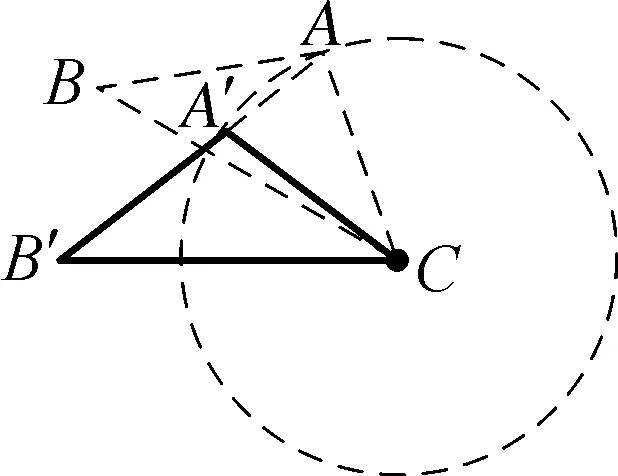
图5
点评:本题中图形旋转问题的难点在于找到一条过定点的未知直线,可以借助于“旋转可逆”的规律,将此难点问题转化为“在已知直线上寻找未知点”,再次转化为“直线至旋转中心距离不变”,问题迎刃而解.可见,图形旋转问题中“旋转可逆”的规律,能够有效降低问题的难度.
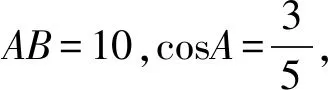
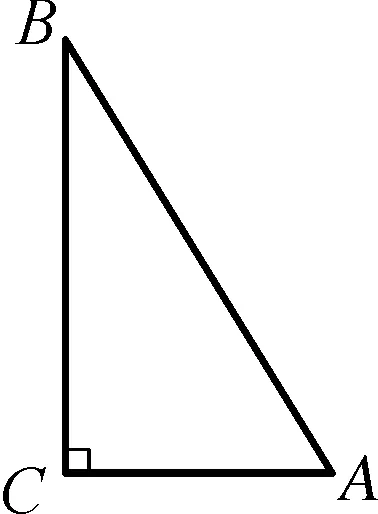
图6
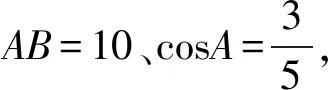
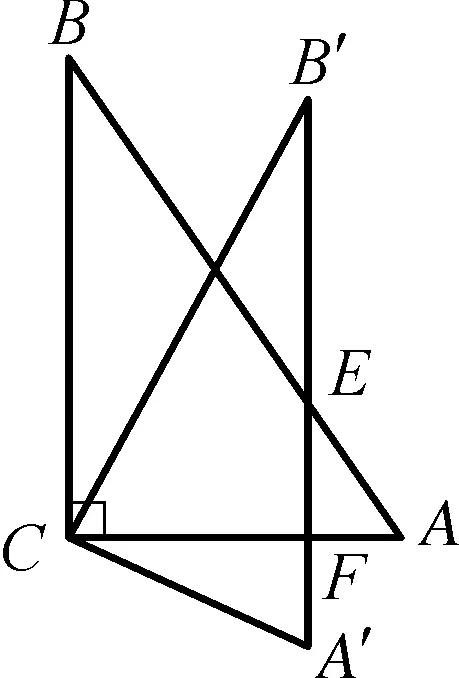
图7
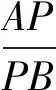
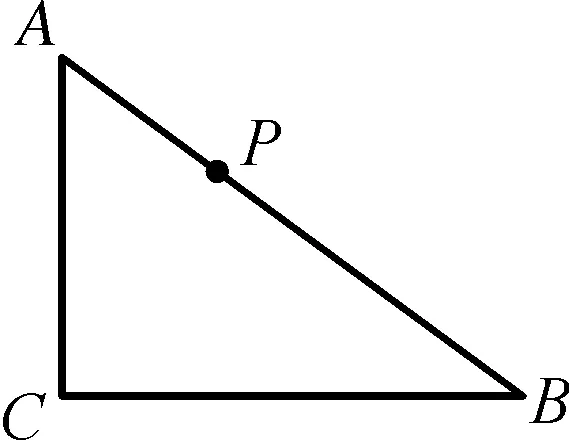
图8
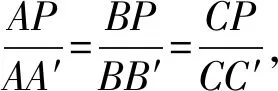
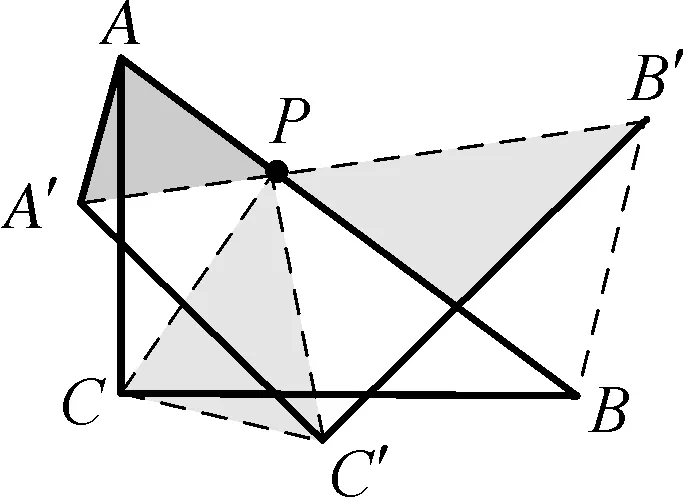
图9
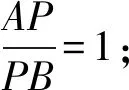
点评:本题是图形旋转的典型题型之一,从旋转规律可知对应点与旋转中心连线所成角度与旋转角度相等,连接三点构成的等腰三角形均为相似三角形,利用相似三角形对应边的比例关系有效实现问题的等价转化,让学生理解旋转问题本质,厘清解题思路,实现高效解题.
变式2如图10所示的直角△ACB中,AC⊥BC,BC=3,AC=4,∠ABC的角平分线BD交AC于D,现以A点为旋转中心将△ABC旋转一定的角度后记为△AB′C′,若B′点处于BD射线之上,试求:线段CC′的长度.
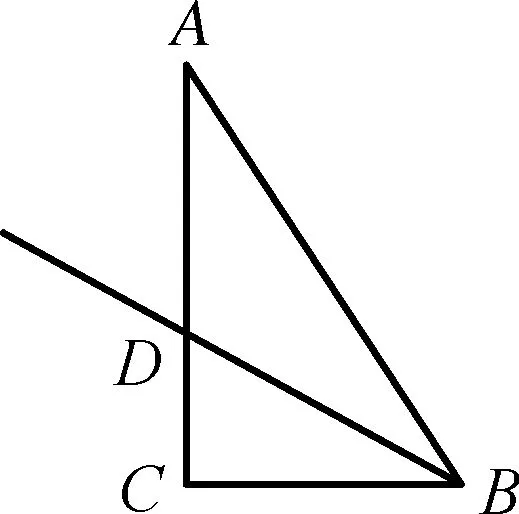
图10
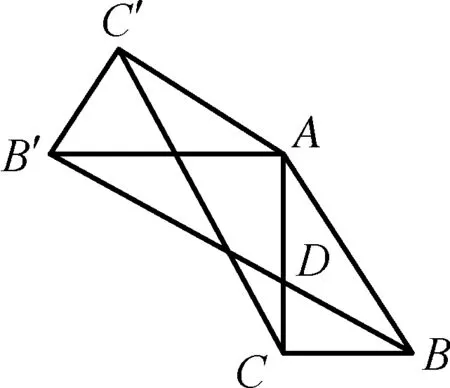
图11

3 结束语
在图形旋转问题中,问题的难点在于旋转前后图形位置的确定,本文案例中呈现旋转规律解题、作草图解题都是解决图形旋转问题的重要方法,掌握这类解决问题的方法要求学生具备一定的逻辑思维能力和理性思维水平,对于初中数学教师而言,在平时的课堂教学中,应该以“形”为研究对象,引导学生挖掘“几何图形”旋转的本质规律,不断提升学生的逻辑思维能力,进而提升学生数学学科核心素养.

