基于代理模型技术的玻璃纤维复合装甲抗弹性能多目标优化设计

王 威， 胡鹏程， 张 攀， 刘 均， 程远胜

(华中科技大学 船舶与海洋工程学院，武汉 430074)

纤维增强复合材料因其质量较轻、强度和模量高、抗疲劳性能好等优点，广泛应用于抗弹防护等领域[1]。纤维增强复合材料主要由纤维和基体组合而成。在复合材料中，纤维通常按照一定方式铺设。常见的布置方式有单向布置、二维布置和三维布置。特殊的布置方式使得材料在整体上呈现出远超单根纤维的优良力学特性[2]。纤维对材料起增强作用，其种类繁多，常用的高性能抗弹纤维有芳纶纤维、超高分子量聚乙烯纤维、玻璃纤维[3]等。纤维增强复合材料的抗弹性能一直受到国内外学者的广泛关注，研究重点集中在其受到冲击载荷时的弹道极限、失效形式和吸能机制等[4]。随着计算机技术的高速发展，数值方法已成为弹道冲击领域最常用的方法，与弹道试验和理论分析相结合的研究思路被广泛使用。

目前，建立纤维增强复合材料板数值模型的方法主要有两种：连续均质模型和微观结构模型[5]。前者将整个材料简化为具有正交各向异性的均质材料，后者则用两种材料还原纤维和基体结构。连续均质模型不能完全反映复合材料的失效方式，但其优点是简便、耗费的计算资源更少，目前仍使用较多。

为使防护装甲能够适应多种类型的冲击工况，多层板复合装甲的设计思路被提出，将不同类型的材料组合在一起使之具备更优良的防护性能[6]。针对复合装甲的抗弹性能已开展了一些相关研究[7-10]。对于由多种材料、多个结构组成的复合装甲，它的抗弹性能直接受到自身结构参数的影响，如前后面板的厚度、芯层厚度等，选择合适的结构参数能够让复合装甲的防护效果达到最佳[11-13]。

若芯层结构为波纹结构、蜂窝结构、梯形结构等复杂结构，或者复合装甲的板层数量较多，那么整个复合装甲抗弹性能的影响因素会更多。通过试验方法或数值方法进行参数研究可以定性分析这些结构参数对抗弹性能的影响，而理论解析方法在面对这种材料组分多、结构复杂的情况时，很难得到较精确的结果。结构参数较多的复合装甲结构，往往会构成数目较多的组合方式，若采用有限元方法探索最优结构设计方案将会非常耗时。

针对这类耗时的优化问题，可以采用代理模型技术进行解决。通过利用少量的高精度结果数据，选择合适的数学模型，近似预估其他参数下的输出结果，可以大大缩短分析时间，提高优化速度[14]。基于代理模型技术对结构力学性能开展优化设计研究的方法获得了一些学者的关注。Qi等[15]以三明治板面板厚度和泡沫铝密度为设计参数，采用人工神经网络代理模型和NSGA-Ⅱ优化算法，对泡沫铝夹芯三明治板结构的防爆性能进行了优化设计。Chen等[16]采用多项式响应面代理模型，建立了蜂窝夹层结构在垂直和45°倾斜载荷下吸能特性与结构参数之间的关系，进而通过多目标遗传算法对结构进行了轻量化设计。Cai等[17]基于Kriging模型，建立了金属波纹芯层夹层结构的抗爆性能和面板厚度、波纹芯层厚度、高度和倾斜角度间的关系，并对结构最大挠度和比吸能量进行了多目标优化设计。

本研究将以由高强度钢面板和玻璃纤维增强复合材料芯层组成的复合装甲结构为研究对象。将采用有限元分析软件ANSYS/AUTODYN，建立该复合装甲结构弹道行为的数值预报模型，并与文献、试验数据对比验证数值模型的有效性。采用Kriging代理模型技术，建立复合装甲弹道极限速度的快速预报代理模型，通过与有限元结果对比验证代理模型的预报精度，并开展相关性分析。最后，基于构建的代理模型，采用NSGA-Ⅱ算法对复合装甲结构进行多目标优化设计，获得其帕累托前沿曲线，并对初始设计结构提出两种优化方案。

1 玻璃纤维增强复合装甲结构有限元模型

1.1 有限元模型建立

1.1.1 几何模型与网格划分

复合装甲结构由前、后置面板和芯层组成，它们的面内尺寸均为480 mm×480 mm。子弹为圆柱形，直径为12.8 mm，长度为40 mm。利用有限元分析软件AUTODYN 建立弹体和复合装甲的全尺寸模型，采用六面体拉格朗日网格对靶板和弹体进行离散化。弹体直径方向和长度方向分别划分为14份和40份，单元近似为边长1 mm的立方体。靶板面内采用“梯度划分”策略，在冲击中心约两倍弹体直径范围划分1 mm大小网格，离中心越远网格越大，厚度方向单元大小同样为1 mm。靶板结构和弹体的有限元模型，如图1所示。

图1 靶板和弹体的有限元模型Fig.1 Finite element model of target plate and projectile

1.1.2 玻璃纤维增强复合材料层合板材料模型

采用连续均质模型，建立玻璃纤维增强复合材料层合板有限元模型，描述其力学行为的材料模型主要包含状态方程、强度模型、失效模型和侵蚀准则。

固体状态方程用来描述固体材料温度、体积和内部压力之间的关系。由于玻纤复合材料中纤维的规则排列，材料从整体上表现出各向异性，状态方程采用正交各向异性类型。采用非线性体积响应模型，描述高速冲击载荷下玻璃纤维材料的状态变化，其表达式为

(1)

式中：μ为压缩率，μ=ρ/ρ0-1；ρ0为材料未受力时的密度；e为单位质量的材料内能；A1，A2，A3，B0，B1，T1和T2均为材料常数。一般情况下，T1=A1，而A1通常取等效体积模量K，由材料的刚度系数换算得到。仅取非线性状态方程的前两项(A2取10×A1)足以满足该冲击问题的求解精度[18]。

材料强度描述材料何时发生屈服，随后产生塑性应变。选用弹性模型作为玻璃纤维增强复合材料的强度模型，即假定材料为理想弹性材料，不会达到屈服状态，不发生塑性变形。

失效模型用来判断材料何时发生失效，失效后的力学行为发生怎样的变化，分别对应失效准则和后失效响应。在建立材料几何模型以及定义弹性常数时，坐标系中x，y，z方向分别对应材料模型中的3，2，1方向，同时也分别为玻璃纤维板的层内相互正交的纵、横纤维方向和板厚方向。失效准则基于材料的应力和应变响应，即当任意一个应力或应变分量超过设定阈值时，判定材料单元在对应方向上发生失效。因玻璃纤维复合材料具有正交各向异性，各应力、应变分量的失效设定值不同，如表1所示。当11方向应变ε11>0.009时，程序判定该单元发生11方向拉伸失效；当22(33)方向正应力σ22(σ33)>432 MPa、或ε22(ε33)>0.02时，单元发生22(33)方向拉伸失效；当面内切应力τ23>80 MPa时，单元发生面内剪切失效；当同时有两个分量达到设定阈值时，单元发生整体失效，之后将只能承受静水压力。上述不同类型的失效发生后，将会对材料的力学性能产生不同影响，因此失效后材料的力学响应同样呈现各向异性。面内剪切失效和11方向拉伸失效将造成玻璃纤维板的分层现象，而22(33)方向拉伸失效则造成层内对应方向的纤维拉伸失效。失效后，材料的刚度矩阵发生退化，对应方向上杨氏模量减为0；剪切模量均产生折减，剩余剪切刚度分数通常取0.2。

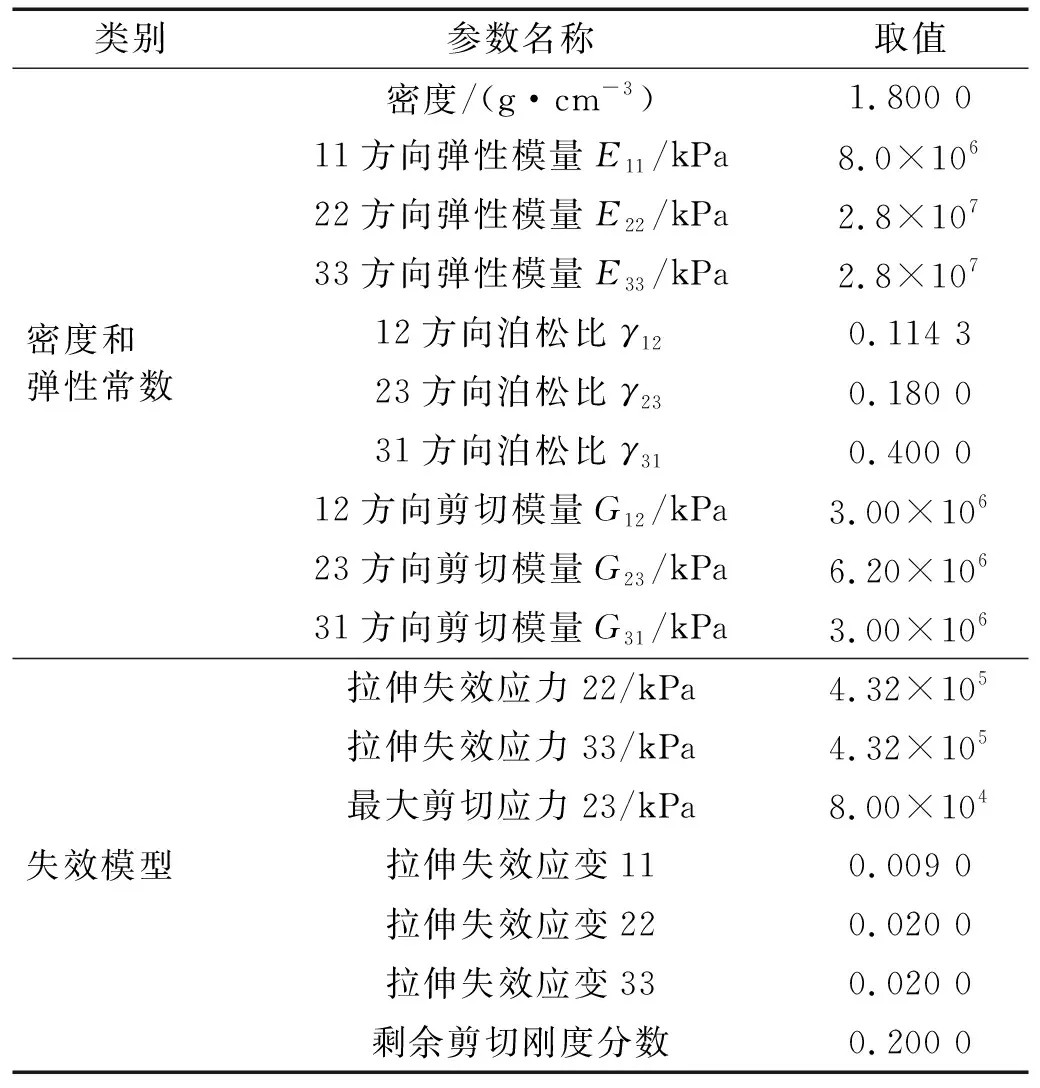
表1 玻璃纤维增强复合材料材料参数[19]Tab.1 Material parameters of glass fiber reinforced polymer

侵蚀准则用来判定何时删除单元。之所以需要对某些单元实行删除操作，是因为当单元的变形程度很大、形状十分扭曲时，时间步长将会变得很小，有限元数值计算过程所需的时间会大大增加，使仿真无法继续下去。为了将时间步长维持在合理范围，保证数值计算顺利进行，当单元变形过大时，会被程序自动删除。采用等效几何应变衡量单元的变形程度，应变阈值取0.8。

1.1.3 钢板和子弹的材料模型

复合装甲结构的面板为高强度钢，侵彻子弹材料为35CrMnSiA钢。两种钢材的动响应力学行为采用相同的材料模型进行模拟。材料模型采用Hugoniot状态方程、Cowper-Symonds模型、基于等效塑性应变的失效准则和基于等效应变的侵蚀准则。具体材料参数取值如表2所示。

表2 某高强度钢和35CrMnSiA钢的材料参数Tab.2 Material parameters of high strength steel and 35CrMnSiA steel

1.1.4 边界条件、初始条件和接触设置

复合装甲面板的4条棱边施加刚性固定边界条件。子弹施加沿靶板法线方向的初速度。

子弹和复合装甲各层之间设置拉格朗日/拉格朗日接触。建立几何模型时，弹体与前置面板间、各层板之间留有0.1 mm的人工间隙，用于满足接触部件之间最小间距要求。累计产生的人工间隙总和为0.5 mm，远小于复合装甲和弹体厚度方向的尺度，可以忽略人工间隙对有限元计算结果的影响。

1.2 有限元模型对比验证

1.2.1 与文献结果对比

文献[20]对纤维增强复合材料的抗弹性能进行了数值仿真，复合材料的纤维为Kevlar纤维，基体为环氧树脂。对应数值仿真结果与文献结果，如图2所示。图2给出了靶板在500 m/s子弹侵彻作用下失效行为的演化过程。随着子弹侵彻深度的不断增加，靶板厚度方向分层失效(11失效)范围在面内和厚度两个方向上延伸，甚至在某些厚度位置达到了靶板边界。靶板背面凸起变形程度不断增大。最终，子弹头部下方变形最严重的部分与靶板主体分离，子弹从背面射出。本节仿真所得剩余速度为298 m/s，与文献曲线图中的数据十分接近，且失效云图在失效模式和失效范围上十分吻合，由此验证了纤维增强复合材料层合板数值模型的有效性。

图2 当入射速度为500 m/s时，纤维增强复合材料 靶板失效模式对比Fig.2 Comparison of damages in glass fiber reinforced polymer plate at different times impacted at 500 m/s

1.2.2 与试验结果对比

在1 300～1 900 m/s高速子弹冲击下，复合装甲结构剩余速度的有限元数值计算结果，如表3所示。当剩余速度恰好为0时，靶板处于穿透与未穿透的临界状态，此时的入射速度称为弹道极限速度，它能在一定程度上反映靶板抵抗破片冲击的能力。在有限元模型中逐渐减小入射速度逼近弹道极限的方法理论上可行，但实际上弹道极限附近工况的数值计算结果受网格划分方式的影响很大，导致所得的剩余速度不可靠。

表3 不同入射速度下，剩余速度的数值仿真结果Tab.3 Numerical results of residual velocity at different impact velocity

目前，国内外学者普遍采用Lambert-Jonas方法估计结构的弹道极限速度，Lambert-Jonas方程的表达式为

(2)

式中：vi，vr和vbl分别为子弹入射速度、剩余速度和结构弹道极限速度；a，p为待定参数，由一组入射速度、剩余速度的值和最小二乘法确定。将表1中的数据代入Lambert-Jonas方程中，拟合得到a=0.46，p=2.81，弹道极限速度为vbl=1 169.1 m/s，剩余速度-入射速度拟合曲线，如图3所示。

图3 数值入射速度-剩余速度拟合曲线图Fig.3 Fitting curve of impact and residual velocities of numerical simulations

在弹道试验中，用6发子弹以不同入射速度冲击玻璃纤维复合装甲，试验结果如表4所示。6发子弹打靶结果中，3发子弹完全贯穿了复合装甲结构，3发未贯穿，且最大入射速度1 322.9 m/s与最小入射速度1 282.8 m/s间相差40.1 m/s，即6发破片的入射速度在较小的速度范围内，那么该6发子弹的入射速度平均值可作为v50弹道极限速度，得到v50=1 301.8 m/s。对比数值弹道极限速度vbl和试验弹道极限速度v50，两者间的误差为10.2%，该相对误差大小对于弹道极限速度的预测而言在可接受的范围之内，可认为所建立的有限元数值模型在预测剩余速度和弹道极限速度方面可靠性较好。

表4 6发弹道试验结果数据表Tab.4 Results of the ballistic test

弹道试验靶板毁伤容貌，如图4所示。在冲击弹孔附近，靶板受到严重破坏。纤维由于破片的冲击，被拉断或剪断；大量玻璃纤维脱离基体材料，在靶板中间的冲击断口处可观察到纤维的自由端；甚至部分纤维发生外翻，在靶板的上下表面观察到裸露在外的玻璃纤维，上表面的外翻区域面积更大，而下表面的范围更集中、外翻程度更严重。复合装甲结构的表面和剖面均能观察到泛白区域，这是子层间的分离造成的，即分层失效现象。

图4 1 379.8 m/s冲击速度下芯层结构的试验毁伤容貌Fig.4 Post-impacted core from experiment impacted at 1 379.8 m/s

数值模型预报的靶板失效容貌，如图5所示。从剖面图可以看到，靶板内部的主要失效模式为厚度方向拉伸失效(11失效)和整体失效。从俯视图中得到，靶板表面的主要失效模式为厚度方向拉伸失效(11失效)和层间剪切失效(23失效)。预测的失效容貌中厚度拉伸失效和层间剪切失效都将造成靶板厚度方向分层失效，而整体失效则对应靶板中纤维和基体的严重破坏。

图5 1 379.8 m/s冲击速度下玻璃纤维增强复合材料 芯层结构失效容貌的数值预测结果Fig.5 Predicted damage pattern of GFRP core impacted at 1 379.8 m/s

对比数值仿真和弹道试验的靶板失效容貌图，弹孔附近和靶板表面的失效模式、失效范围基本一致。同时，数值模型对弹道极限速度的预测精度较好，可认为所构建的有限元模型可用于预报复合装甲的抗弹性能。

2 复合装甲抗弹性能快速预报代理模型

2.1 Kriging代理模型

复合装甲抗弹性能的一个重要指标是弹道极限速度，它指子弹穿透结构的临界速度。目前，数值弹道极限速度普遍采用Lambert-Jonas方程拟合得到，需要计算4～6个入射速度下的剩余速度。虽然有限元数值方法具有足够的求解精度，但是计算所需的时间往往较长，对结构弹道极限速度的预测更是需要多个工况的结果。代理模型方法很好地解决这个难题，根据已知的一定数目样本点，选用合适的数学模型，给出近似结果。在舍弃部分求解精度的情况下，大大缩短抗弹性能的预测时间。选择采用Kriging代理模型技术，建立弹道极限速度与复合装甲结构组成部件厚度参数之间的函数关系。

假设前置面板厚度tf、芯层厚度tc和后置面板厚度tb的取值范围分别为4～12 mm，20～60 mm和4～12 mm。采用全试验设计方法，在该设计空间内均匀选取样本点，每个设计变量取3个点，一共组成27个样本点，样本点设计变量具体取值，如表5所示。每个样本点计算4～6个入射速度下的剩余速度，共计132个计算工况。利用这27个样本点，建立弹道极限速度vbl与板厚tf，tc，tb之间的Kriging模型。

表5 设计变量的样本点取值Tab.5 Sample values for design variables

2.2 代理模型精度检验

子弹冲击复合装甲问题尚未提出比较成熟的理论解析解，而在建立代理模型时，不关心具体物理过程，将该过程抽象为一个拥有输入变量和输出变量的系统，所以事先无法判断所选代理模型是否合适，从而需要在模型建立之后进行精度检验。

在设计空间内随机生成10个设计方案作为模型精度分析的检测点，比较代理模型预报值和有限元数值计算弹道极限速度之间的误差。采用相对误差ER和归一化均方根偏差DNR评估误差大小，计算表达式如下

(3)

(4)

表6 代理模型预报精度检验结果Tab.6 Accuracy evaluation of predicted results by surrogate model

2.3 变量相关性分析

除了用弹道极限速度表征抗弹性能之外，靶板面密度也是复合装甲性能的重要指标之一，具体表达式为

A=ρftf+ρctc+ρbtb

(5)

式中：A为靶板面密度；ρf，ρc，ρb分别为前置面板密度、芯板密度和后置面板材料密度。

为了分析结构参数对复合装甲抗弹性能的影响程度，有必要对3个板厚参数、弹道极限速度和靶板面密度进行相关性分析。Pearson相关系数可用于衡量两个变量间的线性相关性，具体计算表达式为

(6)

相关性分析结果，如表7所示。由表7可知，3个结构参数之间的相关系数均为0，意味着它们没有线性相关性，这是因为它们随机选取、相互独立。弹道极限速度与3个板厚间的相关系数均大于0，说明随着厚度的增加，复合装甲的抗冲击能力提高。其中，弹道极限速度与复合装甲芯层厚度间的线性相关性最强，为强相关；与前置面板厚度间的线性相关性次之，为中等程度相关；与背面板厚度间的线性相关性最弱，为弱相关。复合装甲弹道极限速度和面密度间的相关系数为0.98，十分接近1，说明两者间的线性相关程度极高，且呈正相关。两者中一个增大将会同时导致另一个增大，这意味着抗弹性能最大化和结构轻量化之间存在矛盾性。

表7 相关性分析结果矩阵Tab.7 The result matrix of correlation analysis

3 复合装甲抗弹性能多目标优化设计

3.1 优化问题描述

弹道极限速度反映结构抵抗子弹侵彻的能力，面密度反映结构的质量。优化设计的目标是提高弹道极限速度的同时降低面密度。由相关性分析结果可知，板厚对复合装甲弹道极限速度和靶板面密度有很大影响，且两者之间呈正相关。显然，两个优化目标之间存在矛盾性，选择合适的结构参数对复合装甲抗弹性能的优化设计十分重要。

设计变量为前置面板厚度tf、芯层厚度tc和背面板厚度tb，目标变量为弹道极限速度vbl和面密度A。优化设计问题的数学模型可表示为

(7)

其中，为便于优化算法求解，用弹道极限速度的相反数表示结构的抗弹能力，使两个目标的优化方向均为最小化。优化算法采用NSGA-Ⅱ多目标遗传算法，它具有计算速度快，结果收敛性好的特点，可在MATLAB工具箱中直接使用。结合已建立的Kriging代理模型，经过反复迭代计算，可获得满足约束条件的最优解。

3.2 优化设计流程

优化设计的主要步骤为：首先，确定优化设计问题中的设计变量与目标变量；然后，构建目标变量和设计变量间的函数关系，并对设计变量施加约束条件，从而建立优化设计数学模型；之后，利用优化算法得到初步优化结果，作出帕累托前沿图；最后，对结果进行讨论，分析优化目标的性能改善情况，结合实际工程需要和初始结构参数提出优化方案。

3.3 多目标优化结果分析

3.3.1 帕累托前沿

相关性分析结果显示，在抗弹复合装甲结构设计中，弹道极限速度和面密度呈现相反的优化方向，不能同时获得最大弹道极限速度和最小面密度。帕累托最优化方法可以处理多个相悖目标变量之间的优化问题。利用MATLAB软件中的多目标遗传算法NSGA-Ⅱ 计算出帕累托最优解集，如图6所示，横坐标为弹道极限速度的相反数-vbl，纵坐标为复合装甲结构的面密度A。

图6 复合装甲结构的帕累托前沿图Fig.6 Pareto fronts of the composite armor

帕累托前沿由一系列“最优解点”构成，不存在目标变量均优于“最优解点”的点，所以从图6看帕累托前沿是所有解的边界。当所得的“最优解点”数目足够多时，帕累托前沿可近似看作一条曲线。为得到足够精确的优化方案，设置遗传算法中初始种群大小为1 600，经过120代计算，得到560个帕累托最优解。

帕累托前沿中有两个特殊点：“理想化点”和“拐点”。由图6可知，理想化点为帕累托前沿左右端点的垂直交点，其横坐标为1 334 m/s，纵坐标为9.88 g/cm2。显然，之所以被称为“理想化点”，是因为该点在前沿曲线的左侧，实际无法取得，弹道极限速度的相反数-vbl和复合板面密度A不可能同时取最小值。拐点的定义是帕累托前沿曲线上到理想化点距离最近的点，考虑到横、纵坐标代表的物理量不同，且绝对数值相差很大，此处的距离实际上经过归一化和无量纲化处理，表达式为

(8)

拐点的含义是多个目标变量间的最佳折中取值，求解得到拐点为弹道极限速度830 m/s、靶板面密度15.29 g/cm2，与理想化点的无量纲距离为0.817 1。

初始设计点P0到理想化点的距离为1.255，大于拐点。比较两个点之间的性能差别，拐点较P0点弹道极限速度下降了14.96%，但靶板面密度减小了29.67%。显然，由于多变量间的矛盾关系，拐点只是名义上的最佳方案，具体选择哪种设计方案需要结合工程上的需求和规范。

3.3.2 初始设计点的优化方案

将初始设计点P0对应的目标变量标记于帕累托前沿图中，见图6。点P0位于前沿曲线的右侧，意味着该点不是最优解点，仍具有一定的优化空间。过点P0分别作关于横轴、纵轴的平行线，与前沿曲线交于点P1和点P2。点P1对于初始点P0的优化含义为通过适当改变复合装甲结构的厚度可以在保持靶板面密度不变的前提下提高其弹道极限速度。点P1的弹道极限速度为1 120 m/s，提高了14.75%。同理，在保持复合装甲弹道极限速度相同的前提下还可以降低靶板面密度，点P2的面密度为18.34 g/cm2，相对初始设计方案点P0降低了15.64%。

复合装甲结构优化设计方案P1和P2的有限元计算结果，如表8所示。由结果可知，代理模型的弹道极限速度预报结果与有限元数值结果之间的误差很小，说明优化设计结果的准确性较高。多目标优化设计具体结果，如表9所示。

表8 优化设计点的有限元分析结果Tab.8 Finite element results of the modified structures

表9 多目标优化结果Tab.9 Results of multi-objective optimization

3.3.3 结构参数(设计变量)的变化规律分析

将帕累托前沿点按靶板面密度或者弹道极限速度从小到大排列，作出复合装甲设计参数的取值变化图，如图7所示。XYZ坐标轴分别对应前置面板厚度、芯层厚度和后置面板厚度。假定曲线的起点为(4,20,4)，那么终点为(12,60,12)，分别为设计空间的上、下边界点。曲线从起点至终点的变化过程，表示复合装甲的最佳结构布置随给定面密度或给定弹道极限速度增大的变化情况。由图7可知，曲线在点(12,60,4)之前的部分几乎均位于设计空间的下平面内，而曲线经过点(12,60,4)之后呈现垂直上升的趋势。这意味着在给定面密度较小或者弹道极限速度要求较低时，前置面板和芯层对复合装甲抗弹性能的贡献更大，芯层厚度率先到达上限，然后是前置面板。在两者均达到最大值后，后置面板厚度才从最初的4 mm开始增加。曲线有两个反常变化的地方：当芯层厚度为30～40 mm时，前置面板厚度在降低；当后置面板厚度为8～10 mm时，前置面板厚度减小了。这说明对于不同的面密度和弹道极限速度，复合装甲各部件对抗弹性能贡献的大小关系不完全相同。

图7 复合装甲最优结构参数Fig.7 Optimum structural parameters of the composite armor

4 结 论

基于连续均质模型，建立了弹体侵彻玻璃纤维增强复合装甲结构的数值模型，并采用Kriging法构建了弹道极限速度快速预报代理模型，最终提出了复合装甲结构抗弹性能多目标优化设计数学模型，开展了复合装甲结构优化设计研究，研究结果表明：

(1) 提出的弹体侵彻复合装甲数值模型预报的弹道极限速度和失效模式与文献及弹道试验结果吻合较好。

(2) 采用Kriging代理模型，能准确预报复合装甲结构的弹道极限速度，与有限元结果的相对误差在3%之内，归一化均方根误差为1.39%。

(3) 芯层厚度与复合装甲弹道极限速度的线性相关性最强、后置面板厚度与弹道极限速度的线性相关性最弱；芯层厚度与靶板面密度的线性相关性也最强。弹道极限速度与靶板面密度的线性相关性极强，两个目标具有很强的矛盾性。

(4) 针对典型初始设计方案(前置面板5 mm、后置面板12 mm、芯层51 mm)，通过开展多目标优化设计，保持弹道极限速度不变可使面密度下降15.64%，或者保持面密度不变可使弹道极限速度提升14.75%。

(5) 通过分析最佳结构参数的变化历程，发现在面密度有限时，优先将材料分配给芯层、其次是前置面板、最后是后置面板，采用这种分配策略能够优化复合装甲结构的抗弹性能。