考虑磨损影响的角接触球轴承动力学特性研究

牛荣军， 洛瑞东， 王玉飞， 李鸿亮， 邓四二

(1. 河南科技大学 机电工程学院，河南 洛阳 471003； 2. 洛阳轴承研究所有限公司，河南 洛阳 471039)

对于高温轴承，高温环境下润滑剂黏度降低，摩擦副间润滑膜变薄极易发生润滑失效，同时材料热膨胀系数不一致，造成工作游隙减小，加剧运动摩擦副间的摩擦磨损[1-2]。因此，在高温和低黏度润滑环境下，轴承工作过程中极易发生磨损，造成其内部游隙和工作面精度变化，从而诱导轴承性能渐变失效[3-4]。严重磨损后，轴承的振动与噪声加剧，运行平稳性变差，导致安装该类型轴承的主机在工作时常出现各种异常振动，严重影响主机的安全性[5]。因而，开展特殊工况下轴承材料摩擦磨损和动力学特性研究，揭示磨损过程中轴承的动态特性渐变规律，对于有效防止此类轴承过早精度失效，延长主机装备的使用寿命具有重要意义。

近年来，在轴承动力学特性和减振降噪方面已开展广泛研究，并取得了一定的进展。Ellis等[6-7]从摩擦动力学的角度出发，建立接触副的弹性接触振动模型。Niu等[8]建立了具有缺陷的球轴承动态模型，对缺陷轴承的振动特性进行了分析。Gu等[9]建立了角接触球轴承的广义时变分段非线性动力学模型，对其动态特性进行了研究，特别是考虑了磨损和滚动接触的耦合效应。Jang等[10]考虑了动态载荷下由于轴承表面磨损和轴错位引起的油膜厚度变化，评估磨损对发动机轴承性能的影响，仿真结果表明磨损与接触压力直接相关。Sawalhi等[11]针对轴承外圈滚道局部剥落进行动力学建模分析，但该模型只考虑了双列球轴承其中一列滚道出现故障的情况。剡昌锋等[12]考虑了润滑对轴承振动的作用，建立了两自由度深沟球轴承局部缺陷动力学模型。随后，剡昌锋等[13]对该模型进行改进，并通过数值仿真与试验验证加入滑动因素对轴承动态特性的影响。刘永强等[14]充分考虑轴承间隙和赫兹接触力等因素，建立了一种外圈缺陷的滚子轴承非线性动力学模型，通过模型模拟和试验对比分析其动力学响应。刘晓玲等[15]研究组件温度对球轴承热冲击流变润滑性能的影响，并对极端工况下的热失效现象进行分析。结果表明在极端工况下，轴承内圈与滚动体之间出现了高压、高温和低膜厚现象。此外，刘晓玲等[16]建立了动态微观弹流润滑模型，给出了表面凸起和凹坑两种点缺陷建模方法，研究表明缺陷尺寸和形态对润滑性能影响显著。

综上所述，目前滚动轴承动力学特性的研究一般都是基于正常条件下开展轴承动力学特性的仿真和试验研究。但在特殊高温和低黏度润滑条件下，因轴承磨损对轴承动力学性能的影响研究还不够充分。本文针对某一高温轴承特殊工况条件，基于固体磨损理论和试验测试，考虑磨损对轴承内部游隙、接触刚度以及高温变形等非线性影响因素，建立角接触球轴承磨损条件下的动力学模型，基于动力学模型的数值求解结果，系统分析磨损程度对轴承动力学性能的影响规律，并与试验结果进行对比验证，为轴承磨损条件下轴承动态特性评估提供理论参考依据。

1 高温轴承滚道磨损模型建立

1.1 轴承材料磨损系数确定

磨损率是磨损计算的一个基本量，根据摩擦学理论可以知道磨损率不仅取决于材料本身的性能，还与工况条件有密切关系。在计算宏观磨损时应用最广泛的模型为Archard模型[17]，磨损率表达式为

(1)

式中：w为瞬时磨损率；K为Archard磨损系数；Q为瞬时法向负荷；u为滑动速度；H为洛氏硬度。

在式(1)中，磨损系数K可以通过具有相同材料性质和润滑条件的球-盘磨损试验得出。以轴承套圈所使用的高温无磁合金材料GH05制成试验对磨圆盘(Φ50.8 mm×6.0 mm)，试验材料热处理方法与轴承加工工艺一致，常温硬度满足58.5HRC，高温300 ℃满足55.0HRC。圆盘表面加工质量与轴承套圈设计要求一致，表面粗糙度小于0.063 μm。试验钢球直接选用轴承的钢球(Φ6.3 mm)，精度等级达到G16级。利用圆盘试样与钢球对磨完成摩擦磨损试验，该试验所采用的试验设备是Rtec高温摩擦磨损试验机，试验机的整体结构如图1所示。

图1 高温球盘摩擦磨损试验机Fig.1 High temperature ball disc friction and wear tester

图2为高温300 ℃，试验载荷为150 N，转速80 r/min钢球和套圈材料制成的圆盘对磨120 min，两次测试的摩擦因数变化曲线。由图2可以看出，高温环境下(300 ℃)，轴承套圈材料的摩擦因数在整个摩擦试验过程中稳定性较好，波动范围小。当径向载荷为150 N时，材料的摩擦因数在0.42左右波动。

图2 高温轴承材料摩擦因数时间历程变化Fig.2 Time course variation of friction coefficient of high temperature bearing materials

由圆盘试样的磨损轮廓图3可以看出，在高温条件下轴承材料的磨损轮廓均比较清晰，呈现出明显的犁沟磨痕。通过三维形貌的的磨损截面计算，获取其在试验载荷和速度条件下的磨损体积，进而获取其磨损系数，具体结果如表1所示。

图3 高温轴承材料磨损形貌Fig.3 Wear morphology of high temperature bearing materials

根据表1不同载荷下球-盘试验数据，可以得了出钢球与滚道间的平均磨损系数K≈2.83×10-7λ-1，λ为油膜润滑参数。

表1 磨损系数试验结果Tab.1 Test results of wear coefficient

润滑膜参数λ同时考虑了粗糙度和润滑膜厚度两个因素，体现出二者对润滑状态的联合作用，可表示为

(2)

1.2 套圈沟道磨损量计算

在球轴承中，接触载荷与滑动速度的乘积Qu的表达式为

(3)

式中：p(x,y)为接触区域中(x,y)点的局部压力；u(x,y)为(x,y)点的局部滑动速度；a，b为接触椭圆的长、短半轴。

参照图4的局部接触区域打滑速度u由滑动速度ud和自旋速度us，可得到速度u在x和y方向的分量

图4 接触区域任一点局部滑动速度Fig.4 Local sliding velocity at any point in contact area

(4)

根据Archard模型，将式(3)代入式(4)可以得到单个轴承套圈在时间t内的沟道磨损量Δ的表达式为

(5)

参考内外沟道磨损原理图5，轴承在高温环境下工作一段t时间后，假定钢球与内、外滚道磨损量分别为Δi和Δe。由于磨损导致的内、外沟道沟曲率半径变化量分别为

图5 磨损后沟道曲率半径变化Fig.5 Change of groove curvature radius after wear

(6)

(7)

式中：d′m为考虑热变形之后轴承的节圆直径，d′m=0.5(di+u′i+de+u′e)；D′w为钢球热膨胀后直径；α′i，α′e为考虑温度影响后的内、外接触角； Δri和Δre分别为磨损后轴承沟道半径的变化量；ai，ae分别为钢球与内滚道、外滚道之间接触椭圆区域的长半轴。

高温环境下磨损后的沟曲率半径系数为

(8)

可得到高温下磨损后球轴承的接触角

(9)

进而得到高温下磨损后球轴承的径向游隙

u′r=2(Δri+Δre)+ur

(10)

2 轴承磨损条件下动力模型建立

高温角接触球轴承的动力模型原理图，如图6所示。

图6 角接触球轴承的动态力学模型Fig.6 Dynamic mechanical model of angular contact ball bearing

通过图7可以得到，任意时刻为t时，轴承内部第j个滚动体所在的位置角Ψj的表达式为

图7 滚动体位置角Fig.7 Position angle of rolling element

(11)

(12)

当轴承发生磨损t时后，第j个钢球与滚道间的接触变形量为

(13)

1.2节已经推导了高温环境下轴承结构参数的计算公式以及考虑温度影响的轴承变形-协调方程，联立1.2节所推导的公式，可以得到任意时刻t时，高温环境下磨损后角接触球轴承的接触变形表达式为

(14)

将磨损后角接触球轴承的接触变形表达式(14)代入式(12)，可得到任意时刻为t时轴承第j个滚动体与滚道之间的综合接触载荷为

(15)

在t时刻，钢球与滚道之间的接触角可表示为

(16)

对于角接触球轴承，在t时刻的接触作用力和力矩为所有钢球所承受的接触负荷之和，钢球产生的接触载荷和力矩分解到坐标轴上的示意图，如图8所示。

图8 轴承接触作用力和力矩示意图Fig.8 Schematic diagram of bearing contact force and moment

(17)

式中：Qx(t)为钢球在t时刻产生的接触力在x轴分量；Qy(t)为钢球在t时刻产生的接触力在y轴分量；Qz(t)为钢球在t时刻产生的接触力在z轴分量。

将钢球产生的力矩分别分解到x，y坐标轴方向上

(18)

(19)

式中：Mx(t)为钢球在t时刻产生的力矩在x轴(径向)分量；My(t)为钢球在t时刻产生的力矩在y轴(径向)分量。

根据角接触球轴承受载图，可以推导出考虑磨损影响的角接触球轴承的动力学方程组

(20)

图9 轴承动力学模型计算框图Fig.9 Calculation block diagram of dynamic model of bearing

3 计算及结果分析

以某一高温环境角接触球轴承7009为研究对象，轴承安装方式为外圈固定，内圈旋转，轴承主要参数，如表2所示。在第2章高温轴承磨损动力学模型的基础上，对轴承的外加载荷、工作转速以及由于磨损导致的结构参数的变化等进行设置，研究高温角接触球轴承的动态特性，对比分析轴承磨损前后动态性能的变化，为此类轴承的故障预测和结构优化设计提供理论依据。

表2 轴承计算参数Tab.2 Calculation parameters of bearing

3.1 载荷对套圈沟道磨损率的影响

当径向游隙取0.01 mm，内圈转速取80 r/min，环境温度为300 ℃时，轴向预紧力和径向载荷联合作用下，轴承内、外套圈磨损率的变化情况，如图10所示。

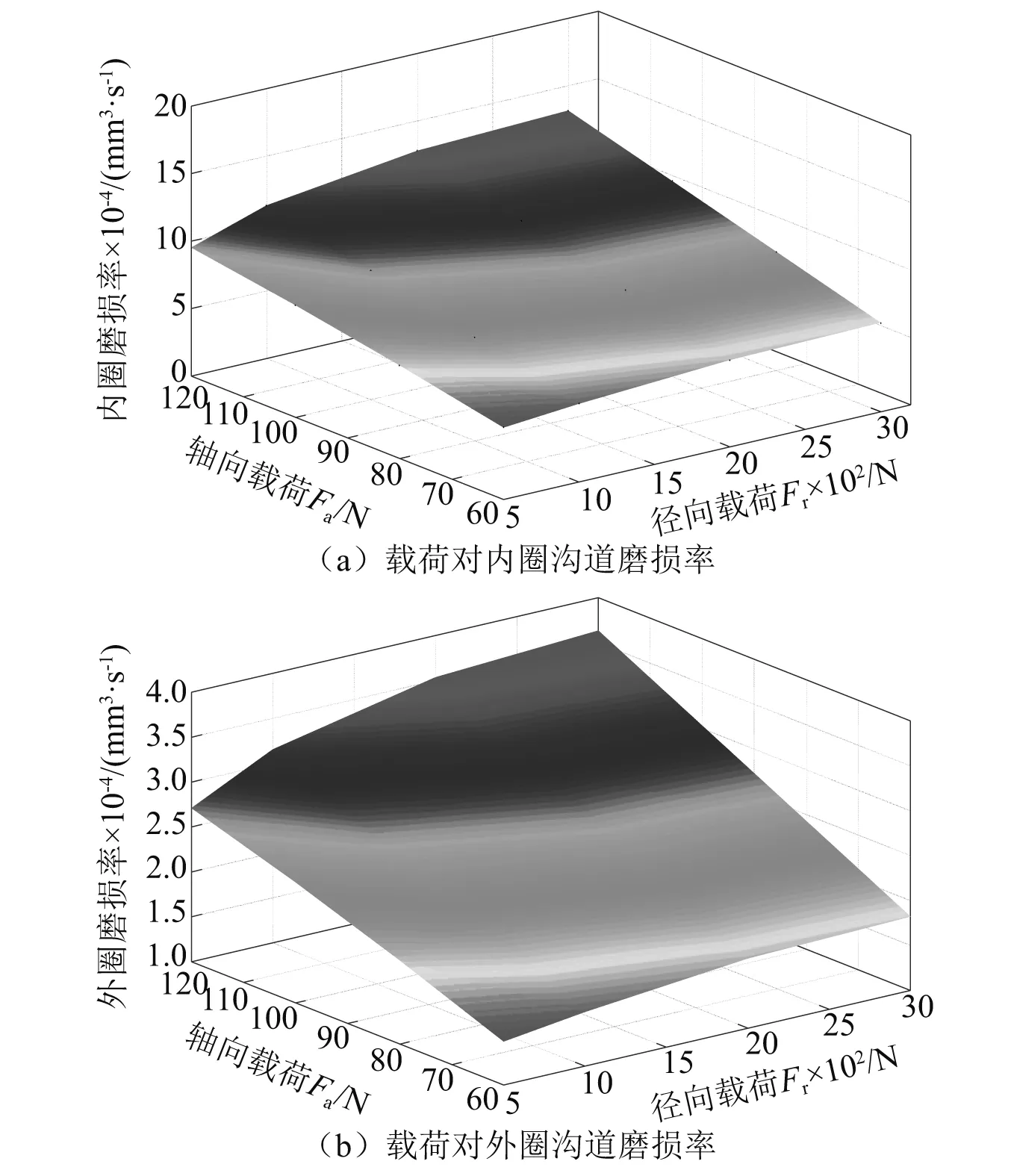
图10 载荷对套圈沟道磨损率的影响Fig.10 Effect of load on wear rate of rings raceway

(1) 通过图10可以看出，随着径向载荷和轴向载荷的增加，内圈和外圈的磨损率均变大，表现在三维图上为右上角翘起，左下角下沉。其原因为：当轴承承受的外加载荷变大，每个滚动体所承受的接触载荷和应力变大，滚动体与滚道间的摩擦力变大，轴承摩擦磨损严重。

(2) 从图10(a)可以看出，内圈磨损率受到径向和轴向载荷的影响程度相当，而从图10(b)可以看出，外圈磨损率受到轴向载荷的影响明显大于受到径向载荷的影响作用。

(3) 对比图10(a)和10(b)可以看出，在相同载荷工况下，内圈磨损率的数量级比外圈大。

3.2 沟曲率半径系数对沟道磨损率的影响

当径向载荷取3 000 N，轴向预紧力为100 N，内圈转速为80 r/min，环境温度为300 ℃时，不同内、外沟曲率半径系数与轴承内、外套圈磨损率之间的关系图，如图11所示。

图11 沟曲率半径系数对套圈沟道磨损率的影响Fig.11 Effect of groove curvature radius coefficient on wear rate of rings raceway

(1) 从图11(a)可以看出，内圈磨损率随着内沟曲率半径系数的增大而减小，且当内沟曲率半径系数较小时，内圈磨损率减小的速度快，当内沟曲率半经系数较大时，内圈磨损率减小速度放缓。

(2) 从图11(b)可以看出，外圈磨损率随着内沟曲率半径系数的增大而增大，随着外沟曲率半径系数的增大而减小。

对比图11(a)和图11(b)可知，在内圈曲率半径系数0.515～0.545和外圈沟曲率半径系数0.525～0.550内，内沟曲率半径系数取值最小而外沟曲率半径系数取值大时，内圈磨损率最大而外圈磨损率最小。这说明沟曲率半径系数对轴承内圈和外圈磨损率的影响差异很大，在考虑轴承整个使用寿命时，应该综合考虑内外沟曲率半经系数对内、外套圈磨损率的影响。

3.3 磨损对轴承动力学特性的影响

为了探讨磨损程度对角接触球轴承动力学特性的影响，设置初始径向游隙为0.08 mm，转速为120 r/min，径向载荷为1 000 N，轴向预紧力为100 N，高温环境下轴承磨损时间分别为0，450 h，750 h，1 200 h时，对轴承外圈y方向上的振动位移变化进行分析，得到轴承在不同磨损程度下的振动位移变化图，如图12所示。

通过图12可知：

(1) 当轴承未发生磨损时，振动位移的幅值变化范围为0～0.075 mm，轴承发生磨损后，振动位移幅值随着磨损程度的加重而变大，当磨损时间为1 200 h时，振动位移幅值的变化范围为0～0.105 mm。

(2) 随着轴承磨损时间的延长，轴承磨损程度加重，振动位移波动性变大，周期性不明显，这说明在一定参数范围内，当角接触球轴承发生磨损，随着磨损程度的加深，其振动波动性变大，规律性变差。这是因为，轴承发生严重磨损后，内部游隙变大，振动噪声加剧。

当初始径向游隙为0.08 mm，转速为120 r/min，径向载荷为1 000 N，轴向预紧载荷为100 N，高温环境下磨损时间分别为0，450 h，750 h，1 200 h时，角接触球轴承的振动速度变化图，如图13所示。

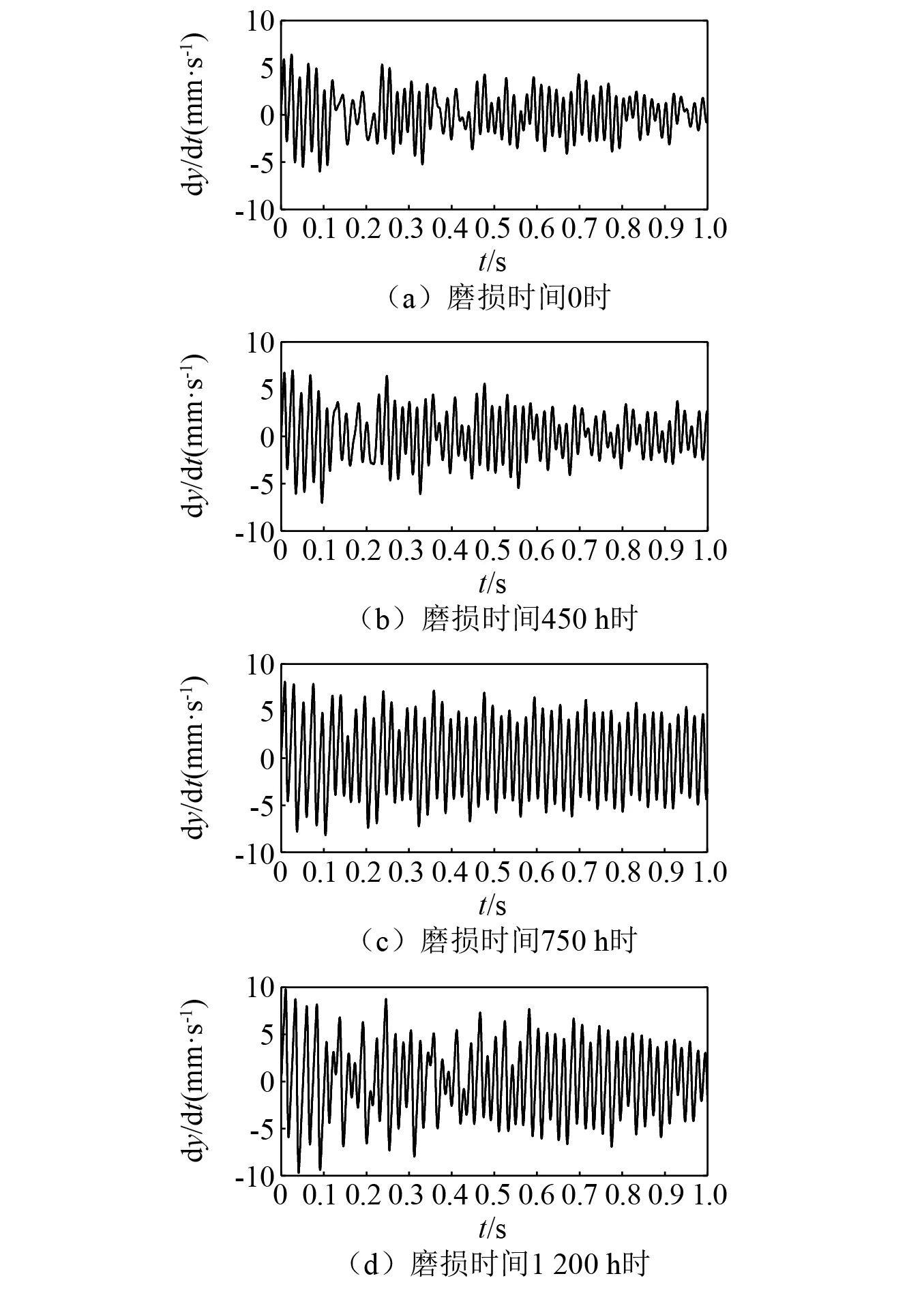
图13 不同磨损程度下的振动速度变化Fig.13 Changes of vibration velocity under different wear degree

由图13可以发现：

(1) 当轴承未发生磨损时，轴承振动速度波动性大，无明显周期性；而当轴承发生轻微的磨损，振动速度的规律性变强，波动性降低；当轴承进一步磨损，振动速度变化呈现出较好的周期性，规律性变强且波动性降低，这说明在0～750 h内，沟道磨损程度虽逐渐加深，但轴承仍能够保持较好的运动平稳性。

(2) 从图13(d)可知，当轴承磨损程度进一步加重，振动速度波动性变大，周期性变差，这说明在1 200 h轴承发生严重磨损，其轴承的运动平稳性恶化，振动噪声变大。

对比图13分析结果可知，当轴承磨损程度较轻微时，轴承的磨损会使得轴承的运动稳定性得到一定改善，但当轴承磨损较严重后，其振动噪声急剧增大，影响运动状态的平稳性，通过振动速度监测可评判轴承精度是否失效。

当转速为120 r/min，径向载荷为1 000 N，轴向预紧力为100 N，高温环境下轴承磨损时间分别为0，450 h，750 h，1 200 h时，角接触球轴承质心轨迹，如图14所示。

图14 不同磨损程度下的质心轨迹变化Fig.14 Changes of centroid trajectory under different wear degree

由图14可知：

(1) 轴承磨损初始阶段，z方向的振动幅值与x方向幅值差距不大，但整体来看，运动过程中曲线存在交叉重叠的部分，这说明高温角接触球轴承的运动稳定性较差。

(2) 在0～750 h磨损过程中，z方向的幅值与x方向幅值差越来越大，交叉重叠的部分也越来越多。

(3) 到1 200 h摩擦阶段时，轴承质心轨迹图基本没有规律，x方向幅值和z方向的幅值差别变大，规律性变差，表明此时轴承存在较为严重的振动噪声。

4 计算结果验证

在TMs10-17N轴承试验机上(如图15所示)，对角接触球轴承分别进行450 h，750 h，1 200 h的磨损试验，试验轴承的初始基本参数见表2。试验条件为：径向载荷1 000 N，轴向预紧力100 N，转速80 r/min。每套轴承试验前，都需要先检查试验设备是否处于正常状态，然后设置试验转速，利用加载装置给试验轴承施加载荷，试验过程中，需要利用软件监测轴承的状态。

1.加载装置;2.连接装置;3.加载套;4.压环;5.左套筒;6.腔体; 7.隔离套;8.轴承;9.垫圈;10.右套筒;11.试验轴。图15 试验设备主体图Fig.15 Main appearance of test equipment

图16所示为选取的同一批次出厂的4套轴承，为保证试验前后轴承性能的可比性，对轴承的游隙和振动指标进行复测，试验轴承都满足P5级精度和振动速度指标要求[18]。4套轴承中一套为未进行磨损试验(1号轴承)和3套分别经过450 h(2号轴承)、750 h(3号轴承)、1 200 h(4号轴承)磨损试验后的磨损轴承。轴承磨损前后游隙测试设备，如图17所示。基于建立的轴承磨损性能分析模型，输入试验轴承尺寸结构和工况参数，可以得到轴承不同磨损时间后的游隙值。轴承发生磨损后，游隙的数值计算与试验测试结果，如表3所示。

图16 试验轴承试样Fig.16 Test bearing sample

图17 游隙测试设备Fig.17 Clearance test equipment

表3 轴承游隙的测试与计算比较结果Tab.3 Test and calculation results comparison of bearing clearance

由表3可知，不同磨损时间后，轴承游隙计算结果与试验测试结果趋势基本一致，最大误差在12%以内，满足工程应用要求，从而也验证了所建立的轴承磨损计算模型的可靠性。

以图16所示的经过450 h，750 h，1 200 h试验后的磨损角接触球轴承和未进行磨损试验的轴承为试验对象，采用BVT-8型轴承振动测量仪，如图18所示，分别测试不同载荷、不同转速条件下轴承的振动速度，以此来分析磨损程度对轴承承振动特性的影响，并与数值计算结果进行对比，从而完成验证试验。

图18 振动速度测试设备Fig.18 Test equipment of bearing vibration velocity

按照BVT-8型轴承振动测量仪和振动速度测试标准要求，设置轴向载荷为200 N，试验转速为1 800 r/min，试验测试不同径向载荷下3号轴承的振动速度均方根值(见图19)和仿真计算得到的振动速度均方根值对比结果(见图20)。

图19 不同载荷下轴承振动速度试验测试结果Fig.19 Experimental results of bearing vibration velocity under different loads

图20 载荷对轴承振动速度的影响对比Fig.20 Comparison of load on bearing vibration velocity

通过图20可知，当径向载荷不断增大时，试验值与仿真值随着径向载荷变化的趋势一致。从图20中还可以发现，试验值比仿真值稍大，这是因为试验过程轴承的安装和固定都会影响轴承振动测试结果，同时测试环境对振动结果也有影响，导致试验测试的轴承振动速度均方根值稍大。但是测试得到的结果与理论仿真计算结果在数值上相差很小，在整体变化趋势上二者基本一致，从而验证了本文所建立模型的准确性和合理性。

对磨损时间分别为0，450 h，750 h，1 200 h的4套轴承的振动速度变化规律进行试验测试，试验测试条件为轴向载荷150 N，试验转速1 800 r/min，径向载荷500 N，测试结果如图21所示。

图21 不同磨损程度下轴承振动速度试验测试结果Fig.21 Experimental results of bearing vibration velocity under different wear degree

对测试得到的不同磨损程度轴承的振动速度值进行数据处理，求解得到不同磨损程度下振动速度的均方根值，并与本文所建立的振动模型所得到的振动速度均方根值进行对比，如图22所示。

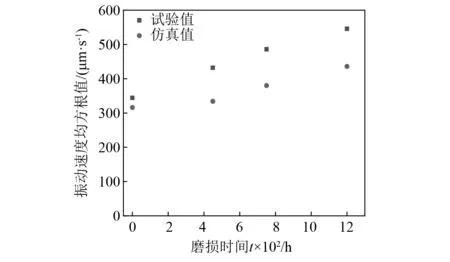
图22 磨损程度对轴承振动速度的影响对比Fig.22 Comparison of wear degree on bearing vibration velocity

通过图22可知，随着轴承磨损程度的加深，轴承的振动速度均方根值不断增加，仿真值与试验值的变化趋势一致。同时可以看出，仿真振动速度均方根值相比于试验振动速度均方根值稍小，其原因分析为：试验环境中存在引起轴承振动的激励因素，同时轴承各零部件的加工质量精度、轴承磨损后其工作面的精度等均会影响其振动特性，导致试验得到的角接触球轴承振动速度均方根值稍大。

5 结 论

对于高温环境下运行的滚动轴承，由于其环境的特殊性，轴承黏度减小，润滑油膜很难充分形成，轴承极易发生磨损，从而影响轴承的振动性能，通过研究得到主要结论为：

(1) 随着载荷的增加，内圈和外圈的磨损率均变大，其中内圈磨损率比外圈磨损率大，在磨损评估中可以主要关注内圈磨损情况。

(2) 当轴承磨损较轻微时，轴承运动稳定性随着磨损时间的延长而得到一定改善，并在一定的磨损周期内能保持较好的运动平稳性，但是当轴承磨损较严重后，其振动噪声急剧增大，运动平稳性恶化。通过振动状态的变化，可作为轴承精度失效的判断依据。

(3) 游隙和振动试验测试结果与计算结果具有较好的趋势一致性，满足工程应用要求，验证所建立的考虑磨损振动模型的准确和有效性。