有限域上椭圆曲线Weil对的计算

胡建军,王 伟,李恒杰

(兰州文理学院 数字媒体学院,兰州 730010)

0 引 言

椭圆曲线上M扭曲的Weil对是密码学领域的一个重要问题,其用于解决椭圆曲线的离散对数和开发密码系统。2004年,Miller[1]较为详实地研究了Weil对的性质和其有效计算,开启了Weil对在公约密码系统中的应用。随后许多学者进行了大量卓有成效的研究,这些关于椭圆曲线Weil对的研究以Miller算法为基础,不仅有大量的理论拓展[2-10],而且还有广泛的应用研究[11-13]。然而,实践研究发现,一些理论和应用研究过分应用了Miller算法,导致部分理论研究需要新的方法支持。为此笔者给出了Weil对计算的3种方法,通过实例指出了Miller算法在有限域上实施计算时点的选择问题,分析了两种不同方法使用Miller算法的差异,指出了运用Miller算法计算Weil对应该注意的问题,验证了利用Weil对计算椭圆曲线的离散对数。通过有限域上椭圆曲线Weil对计算问题的研究,将对已有的理论研究形成挑战,同时对于公约密码体制的应用和推广具有重要的意义。

1 有限域上的椭圆曲线和Weil对的计算

1.1 有限域上的椭圆曲线相关概念[14]

设p>3是一个素数,q=pr,r≥1,E(Fq)表示椭圆曲线上的有限域,E(Fq)上的椭圆曲线E是一个形如E:y2=x3+Ax+B的方程,其中A,B∈Fq,且Δ=-16(4A3+27B2)≠0,点对(x,y)∈Fq×Fq是E上满足方程E:y2=x3+Ax+B的一个解,且要么y=0,要么-4A2-27B3|y2。E(Fq)表示Fq上所有满足方程E:y2=x3+Ax+B解的点集,包括无穷远点O。E(Fq)上“+”运算定义如下

(x,y)+O=O+(x,y)=(x,y)

(1)

(x,y)+(x,-y)=O

(2)

x3=λ2-2x,y3=λ(x-x3)-y

(3)

x3=μ2-x1-x2,y3=μ(x1-x3)-y1

(4)

因此(E(Fq),+)是一个以O为单位元的阿贝尔群。

1.2 扭曲子群和除子的特征

椭圆曲线上的有限阶点是二维的[1]。设K是一个特征为p的域,Ω是K的代数封闭空间,M是一个与p互素的正整数,作为一个阿贝尔群,则有E[M]≅ZM×ZM,其中ZM表示阶为M的循环群。Weil配对是定义在E[M]上点的非退化内积。定义E[M]={T∈E(Fq)|MT=O}是M扭曲点的集合。下面给出一些与Weil配对相关的一些理论。

引理1 设D是E上的除子,如果deg(D)=0,则div(f)=D⟺sum(D)=O[6]。

假设f∘M满足f(M(T))=f(MT),可以验证f∘M和gM有相同的除子,从而令f∘M=gM。

若T,S,T1,T2,S1,S2∈E[M],则

eM(T1+T2,S)=eM(T1,S)eM(T2,S),eM(T,S1+S2)=eM(T,S1)eM(T,S2)

(5)

eM(T,S)=eM(S,T)-1

(6)

eM(T,T)=eM(S,S)=1

(7)

若eM(S,T)=1,则

T=O或S=O

(8)

引理2 假设函数f和h在E上没有公共点,则f(div(h))=h(div(f))[1,8]。

设μM={x∈Fq|xM=1}是Fq中第M个单位根的群,因为M是素数,因而μM是一个循环群。

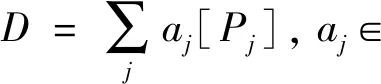
引理4 假设{T1,T2}是E[M]的一个基,则{T1,T2}是E[M]的第M个本原单位根[8]。

定理1 如果eM(T,S)≠1,则T和S线性无关。

证明 假设T和S线性相关,则存在一个整数a,不妨令T被S线性表示,即T=aS。由式(7)可知,eM(T,S)=eM(aS,S)=eM(S,S)a=1,这与假设矛盾,因此结论成立。

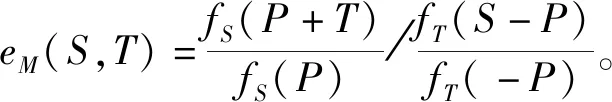
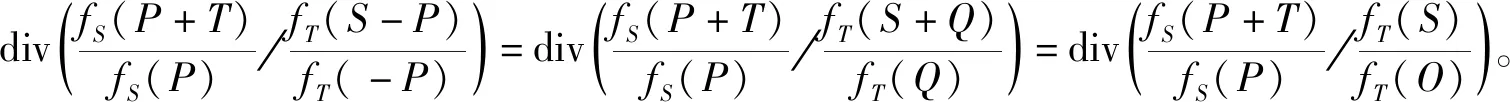
定理3给出了3种计算Weil对的方法。下面是Miller算法理论基础。

假设R=P+Q,经过点R和-R的直线垂直x轴。令经过点P和Q的直线方程为y=kx+m,因为P、Q和R3点共线,则f(x,y)=y-kx-m是椭圆曲线E的一个除子,即div(f)=(P)+(Q)+(-R)。由经过点R和-R的直线垂直x轴可得椭圆曲线E的另一个除子g(x,y)=x-xR。因此,有

(9)

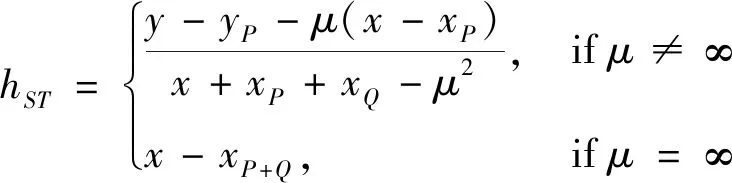
(10)

的定义,其中λ见式(3),μ见式(4)。

下面给出椭圆曲线E上Weil对计算的Miller算法。

算法1 Miller算法[7]。

∥选择X和W。

1) 让X=P+T或P或S-P或-P,W=T或S。

2) 让f=1,n=「log2M⎤,i=n-1,mi=(M)2∥将M转换成二进制表示。

3) 当i>0时,重复执行下列语句序列

f=f2hWW,W=2W。

若mi=1,则f=fhST,W=W+P。

4)返回f。

用下面的方法可以获得阶为M的线性无关的两个点[8]。

算法2 求解阶为M的线性无关的两个点[6]。

按照下列步骤选择S和T。

1) 随机选择一个点P∈E(Fq)。

2) 计算点P的阶N。

4) 重复1)～3)选择S,当S和T线性无关时结束。

2 Weil对计算实例和分析

2.1 Weil对计算实例

为提高计算效率,采用PARI软件和编程相结合的方法计算Weil对。其中椭圆曲线的点由PARI软件的E.gen功能获得,点加和倍乘运算分别利用PARI软件的elladd和ellmul函数获得,其他的数据通过编程实现。下面是一个Miller算法实例。

假设有限域F631上的椭圆曲线E为y2=x3+30x+34,则E(F631)≅Z/5Z×Z/130Z,验证发现点S=(36,60)、T=(121,387)、P=(262,497)、Q=(213,75)和R=(0,36)在曲线上,其中S,T∈E[5],P,Q∈E(F631),P,Q,R的阶均为130,且S和T线性无关,下面给出计算椭圆曲线E的线性对e5(S,T)的过程。

fS(P+T)=fS([483,248])=106,fS(P)=fS([262,497])=42,

fT(-P+S)=fS([465,196])=590,fT(-P)=fS([262,134])=188

由于mod((242)5,631)=1,因此242是e5(S,T)的第5个单位根。

fT(Q+S)=fT([144,241])=487,fT(Q)=fT([213,75])=502,

由于mod((232)5,631)≠1,因此利用定理3和算法1未能计算出e5(S,T)的第5个单位根。

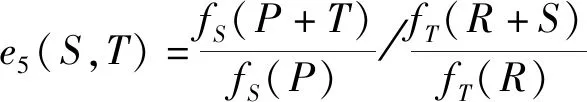
2.2 两种不同Weil对计算方法分析

另外,根据算法2验算可知,点T=(121,387)可以由点P=(262,497)或Q=(213,75)生成,点R=(0,36)不能生成S=(36,60)或T=(121,387)之一。由此可见,计算eM(S,T)与E(Fq)上任意点的选择无关。

3 MOV攻击

1993年,Menezes等[15]提出了一种将椭圆曲线上的对数问题约减到有限域上的对数问题求解算法,简称MOV(Menezes-Okamoto-Vanstone)攻击算法。MOV攻击算法基于Weil配对的求解。

假设S,T,R∈E[M],R∈〈T〉,R=lT,S和T线性无关,则eM(R,S)=eM(lT,S)=(eM(T,S))l。

算法3 MOV算法。

输入:T∈E[M]和R∈〈T〉;

输出:满足R=lT的l。

1) 在E[M]中寻找一个满足S∉〈T〉的S。

2) 计算α=eM(T,S)。

3) 计算β=eM(R,S)。

MOV算法只能求解同阶上的离散对数,不能在小子阶上计算大子阶的离散对数。而MOV算法攻击的实质是求解小子阶上的离散对数。

定理4 假设P,Q∈E[N],Q∈〈P〉,Q=mP,M|N,S,T,R∈E[M],R∈〈T〉,R=lT,S和T线性无关,则求解m是困难的。

证明 假设N=dM,则dP,dQ∈E[M]。不妨令R=dP,则α=eM(T,S),β=eM(R,S)=eM(lT,S)=αl,γ=eM(R,S)m=eM(T,S)ml,由于eM(R,S)M=1,而当M|ml时,γ恒为1。因为m∈{1,2,…,N-1},这样的m不止1个,因此求解m是困难的。

利用2.1的实例数据,验证定理4的结论。

已知Q=7P。令S=26P=(420,483),R=26Q=(121,244),T=(36,60),W=(0,36),则-W=(0,595),S-W=(36,124),W+T=(315,385),R-W=(176,145),利用Miller算法可得

fS(W+T)=176,fS(W)=556,fT(-W)=579,

fT(S-W)=0,fT(R-W)=475,fR(W)=427,fR(W+T)=181。

从而

因此无法有效获得数值7。

当然,如果在130的阶上计算,可得到数值7,但此时的算法复杂度为exp(c(log(qd))1/3(loglog(qd))2/3),其中c是常数,d是椭圆曲线的度。

由此可见,当阶N很大且不是异常曲线时,MOV攻击算法需要很大时间代价,攻击性很弱。

4 结 语

有限域椭圆曲线上的Weil对计算对椭圆曲线密码系统具有重要的作用。笔者给出了计算椭圆曲线第M个本原单位根时,需要选择线性无关的两个阶为M的点,并给出了利用Miller算法计算Weil对时需要使用的公式,分析了两个不同公式之间的差异。同时利用MOV算法验证了Weil对计算椭圆曲线的离散对数,给出了MOV算法的应用领域。通过有限域上椭圆曲线Weil对计算问题的研究,将会对已有的理论研究结果形成挑战,同时对于公约密码体制的应用和推广具有重要的意义。