基于增量更新内涵的形式概念生成算法
吴清寿,郭 磊,余文森
(1.武夷学院 a.数学与计算机学院;b.认知计算与智能信息处理福建省高校重点实验室,福建 武夷山 354300;2.福建农林大学 智慧农林福建省高校重点实验室,福州 350002)
0 引 言
形式概念是形式概念分析(FCA:Formal Concept Analysis)[1]理论的核心数据结构,已在关联分析[2]、信息检索[3]、软件工程[4]和推荐系统[5]等多个领域得到了广泛应用。形式背景中,若多个对象和多个属性存在关系,两者之间的搭配同时达到最大状态就构成一个形式概念,而概念格反映了概念之间的层次关系或泛化-特化关系[6]。在FCA的主要研究方向中,概念生成和概念格构建算法研究是最基础的研究和最根本的问题。
目前在关于概念格构建方法的研究中,根据构造方式的区别,主要包含3类方法:批处理构造、渐进式构造和集成构造算法。批处理算法需要先生成部分或全部格节点(即概念),再处理格节点间的层次关系[7-8]。渐进式算法无需预先获得概念,而是逐个将对象或属性加入到先行概念格中,根据规则对先行概念格进行格节点新增和更新操作,同时修改格节点间的连接关系[9-10]。集成算法是对渐进式算法的泛化,Valtchev等[11]提出了基于二元关系片段并置的格构造方法。概念格构造的主要方式仍然以渐进式方法为主,Zhang等[12]在AddIntent等[13]的基础上提出了FastAddExtent算法,Ma等[14]提出了基于依赖空间模型的概念格构造算法。
在应用中,只需得到形式背景对应的全部概念,而无需关注概念间的层次关系。基于闭包算子求所有闭包的算法NextClosure[15]是一个典型的概念生成算法,其从最小概念出发,逐步选择字典序大于前一个外延的最小外延。重复这个过程,直到找到最大外延。然而NextClosure在判断一个对象集合是否满足最小外延需要多次进行求交集,并且产生了大量无法形成外延的对象集合,而这些对象集合也需要重复进行交集操作,从而导致该算法在概念数较多的形式背景上效率较低[16]。齐红等[17]提出的改进算法SSPCG(Search Space Partition based Concepts Generation)对搜索空间进行划分,通过判断子搜索空间的有效性,避免了对非正规子空间的搜索,生成概念的效率明显提高。卢明等[18]将概念搜索空间组织为前缀树,构建了映射前缀树的属性表,并使用属性表对前缀树中的无效子空间进行剪枝。
笔者提出一种增量更新内涵的概念生成算法IUICG(Incremental Updating Intension based Concepts Generation)。通过任务属性将概念划分为先行概念集合和新增概念集合,缩减了概念比对范围。引入一个外延过滤集合,将无效外延进行过滤,无效外延是不会产生新概念或导致概念更新的外延。遍历任务属性的过程中,根据相关规则产生新概念或对已有概念的内涵进行更新。该过程基于任务属性和已有概念的内涵进行运算,无需对外延中对象间的属性求交集,提高了算法效率。
1 基础理论
定义1 形式背景。形式背景K定义为一个三元组K=(U,M,R),其中U是对象集合,M是属性集合,R⊆U×M,表示U与M的二元关系。通常,将形式背景简称为背景。
对于u∈U,m∈M,若(u,m)∈R,表示对象u具有属性m,记为uRm。
一个背景的例子[19]如表1所示。其中U={1,2,3,4,5,6,7,8},分别表示:水、钢、木、玻璃、汽油、汞、纸和酒。M={a,b,c,d,e,f,g,h,i},分别表示:物质、导电、导热、固定形状、透明、可燃、无固定形状、挥发和可食用。

表1 形式背景示例Tab.1 The example of formal context
例如,2Ra=1表示对象2具有属性a,而2Re=0,表示对象2不具有属性e。
定义2 形式概念。K=(U,M,R)是一个背景,若X⊆U,Y⊆M,令
f(X)={m∈M|∀u∈X,(u,m)∈R},g(Y)={u∈U|∀m∈Y,(u,m)∈R}
若满足f(X)=Y且g(Y)=X,称二元组(X,Y)是一个形式概念(简称为概念)。X是概念(X,Y)的外延,Y是概念(X,Y)的内涵。
如表1所示的背景中,存在一个对象集合X={1,5,8}和一个属性集合Y={a,e,g}。f(X)={a,e,g}=Y,g(Y)={1,5,8}=X,所以二元组({1,5,8},{a,e,g})是一个概念,对象集合{1,5,8}是概念的外延,属性集合{a,e,g}是概念的内涵。
若X={1,4},Y={a,e}。f(X)={a,e}=Y,g(Y)={1,4,5,8}≠X,不满足概念定义,所以二元组({1,4},{a,e})不是一个概念。
定理1[15]设K=(U,M,R)是一个背景,X,X1,X2∈U,Y,Y1,Y2∈M,则有
1)X1⊆X2⟹f(X2)⊆f(X1);
2)Y1⊆Y2⟹g(Y2)⊆g(Y1);
3)X⊆g(f(X));
4)Y⊆f(g(Y));
5)f(X)=f(g(f(X)));
6)g(Y)=g(f(g(Y)));
7)f(X1)∩f(X2)=f(X1∪X2);
8)g(Y1)∩g(Y2)=g(Y1∪Y2)。
定理2 设K=(U,M,R)是一个背景,若X∈U,则(g(f(X)),f(X))一定是概念,若Y∈M,则(g(Y),f(g(Y)))也一定是概念[15]。
定理3 对任意两个概念(X1,Y1)和(X2,Y2),则Y1∩Y2=f(X1)∩f(X2)=f(X1∪X2)一定是内涵,X1∩X2=g(Y1)∩g(Y2)=g(Y1∪Y2)一定是外延[15]。
2 增量更新内涵的概念生成算法
2.1 算法思路
形式概念生成算法中的时间开支主要包括:基于外延求内涵(或基于内涵求外延)的大量交集运算,以及概念生成过程中会产生大量无效的外延(或内涵)。
针对相关问题,笔者提出一种增量更新内涵的概念生成算法,其主要思路为:首先将M中的属性按顺序逐个设置为任务属性,基于任务属性将概念划分为先行概念集合P和新增概念集合Q,分割了概念搜索空间,可避免全域概念比对,提高搜索效率。其次对每个任务属性设置一个外延过滤集合F,利用F将无效外延(不会产生新概念或不会导致概念内涵更新的外延)进行过滤,解决了无效外延重复匹配的问题。提出内涵更新规则,实现增量更新内涵,避免了基于外延求内涵的大量交集运算。
2.2 算法理论
下面对算法中的符号及其含义进行定义,同时提出了概念生成与更新规则。
定义3 任务属性。M中的属性已按照任意顺序排列为M={m1,m2,…,m|M|},根据i=1,2,…,|M|的顺序对mi逐个进行处理,当前正在处理的mi称为任务属性,记为m。
定义4 先行概念集P。M中处理顺序先于m的所有属性(即m1~mi-1)所产生的概念集合称为先行概念集,记为P。Pk表示P中第k个概念,Pa和Pb分别表示P中概念的外延集合和内涵集合,Pk,a和Pk,b分别表示P中第k个概念的外延和内涵,f(Pk,a)=Pk,b,g(Pk,b)=Pk,a。
此处规定P中第1个概念的外延为U,内涵为Ø,即P1,a=U,P1,b=Ø。
定义5 新增概念集Q。对任务属性m,其所产生的所有概念称为新增概念集,记为Q。Q的初始值为Ø。Qj表示Q中第j个概念,Qa和Qb分别表示Q中新增概念的外延集合和内涵集合,Qj,a和Qj,b分别表示Q中第j个概念的外延和内涵,f(Qj,a)=Qj,b,g(Qj,b)=Qj,a。
定义6 候选外延xi。对于任务属性m,令xi=g(m)∩Pi,a,并称xi为候选外延。
定义7 外延过滤集F。一个任务属性m对应一个F。F的初始值为Ø。Fr表示F中第r个元素,且F中元素为二元组Fr=(Fr,a,Fr,c),用Fa表示Fr,a的集合,Fc表示Fr,c的集合。
当xi∉Fa且xi∈Pa,新增Fr=(xi,‘P’)。当x∉Fa,且xi∉Pa∪Qa,则新增Fr=(xi,‘Q’)。
命题1 对于任务属性m,若其产生的候选外延xi满足xi=Qj,a,则Pi,b⊆Qj,b。
证明xi=g(m)∩Pi,a=g(m)∩g(Pi,b),根据定理1中结论8),xi=g(m∪Pi,b)。因为Pi,b⊆m∪Pi,b,根据定理1中结论2),g(m∪Pi,b)⊆g(Pi,b)。因为xi=Qj,a=g(Qj,b),可得g(Qj,b)⊆g(Pi,b)⟹Pi,b⊆Qj,b。
命题2 对于任务属性m,若其产生的候选外延xi满足xi=Pk,a,则m是Pk,b的新增属性。
证明 根据定义6,xi=g(m)∩Pi,a⟹xi⊆g(m),根据定理1中结论1),可知f(g(m))⊆f(xi)。根据定理1中结论4),m⊆f(g(m)),则m⊆f(xi)。因xi=Pk,a,f(xi)=f(Pk,a),所以m⊆f(Pk,a)=Pk,b,即属性m为概念Pk中内涵Pk,b的新增属性。
命题3 对于任务属性m,xi=g(m)∩Pi,a,则xi一定是外延。
证明 因为xi=g(m)∩Pi,a,根据定理2,g(m)一定是外延,而Pi,a也是外延。根据定理3,两个外延的交一定是外延,所以xi一定是外延。
根据算法思路及上述理论,定义笔者算法中的概念操作规则如下。
规则1 外延过滤规则。若xi=Fr,a且Fr,c=‘P’,则无需进行概念操作。
若xi=Fr,a且Fr,c=‘P’,表示xi⊆Pa,且任务属性m已更新到Pb中(xi第1次出现时),所以无需进行概念操作。
规则2Q更新规则。若xi⊆Fa,令Δb=Pi,b-Qj,b,Δb≠Ø,则更新Qj,b←Qj,b∪Δb,否则无需进行概念操作。
当xi=Qj,a,根据命题1,Qj,b=Qj,b∪Pi,b。令Δb=Pi,b-Qj,b,若Δb≠Ø,则Qj,b←Qj,b∪Δb,否则无需进行概念操作。
规则3P更新规则。当xi∉Fa,若xi=Pk,a,则更新概念Pk的内涵为Pk,b←Pk,b∪m,同时更新F←F∪(xi,‘P’)。
xi∉Fa即xi首次出现时,若xi=Pk,a,根据命题2,m是Pk,b的新增属性,所以更新Pk,b←Pk,b∪m。因为xi∉Fa,需要将xi加入Fa,即Fr,a=xi。又因为xi∈Pa,所以对应的Fr,c值为‘P’。
规则4 新增概念规则。若xi∉Fa且xi∉Pa,则新增概念Ql,Ql,a←xi,Ql,b←Pi,b∪m。其中l=|Q|。同时更新F←F∪(xi,‘Q’)。
根据命题3,xi是一个外延。若xi∉Fa且xi∉Pa,则xi是一个新的外延,必然导致新增一个概念。根据命题2的证明可知,m⊆f(xi),同理可得Pi,b⊆f(xi),则m∪Pi,b⊆f(xi)。可知外延xi对应的内涵包含m和Pi,b,所以新增概念为(xi,Pi,b∪m)。
2.3 算法描述
基于上述算法思路和概念操作规则,IUICG的实现步骤如算法1所示。
算法1 IUICG
输入:背景K=(U,M,R)。
输出:概念集合P。
1)P←Ø;Q←Ø
2)F←Ø
3)P1,a←U;P1,b←Ø
4) FOREACHmINMDO:
5)g_m←g(m)
6) FOREACHiIN{1..|P|} DO
7)xi←g_m∩Pi,a
8)r←find(Fa,xi)
9) IFr≠0 THEN
10) IFFr,c=‘P’ THEN
11) CONTINUE
12) ELSE
13)j←find(Qa,xi)
14) IFj≠0 THEN
15) Δb←Pi,b-Qj,b
16) IFΔb≠Ø THEN
17)Qj,b←Qj,b∪Δb
18) ENDIF
19) ENDIF
20) ENDIF
21) ELSE
22)k←find(Pa,xi)
23) IFk≠0 THEN
24)Pk,b←Pk,b∪m
25)F|F|+1,a←xi;F|F|+1,c←‘P’
26) ELSE
27)l←|Q|
28)Ql+1,a←xi
29)Ql+1,b←Pi,b∪m
30)F|F|+1,a←xi;F|F|+1,a←‘Q’
31) ENDIF
32) ENDIF
33) ENDFOR
34)P←P∪Q
35)Q←Ø
36)F←Ø
37) ENDFOR
38) RETURNP。
该算法中,第5行的g(m)用于获取所有包含属性m的对象集合,第10~12行对同一任务属性中重复的外延进行过滤,第13~19行根据规则2判断是否更新Q中的概念内涵。第8行、第13行和第22行的find()函数用于查找xi在F、P或Q中对应的位置,若未找到,返回0,否则返回匹配的元素索引。第22~25行根据规则3判断是否更新P中的概念内涵,第27~30行根据规则4对新增内涵进行操作。
3 实例分析
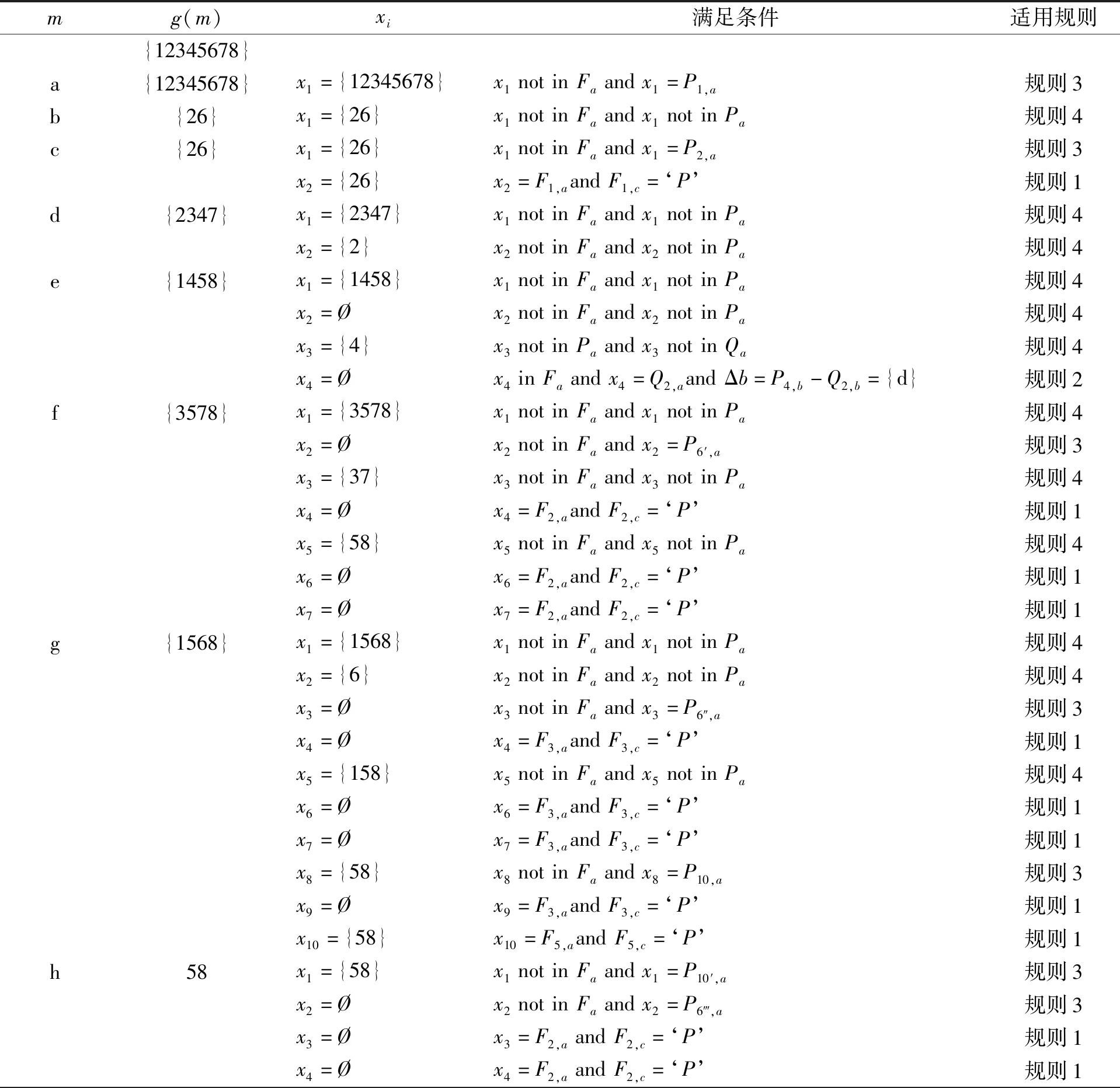
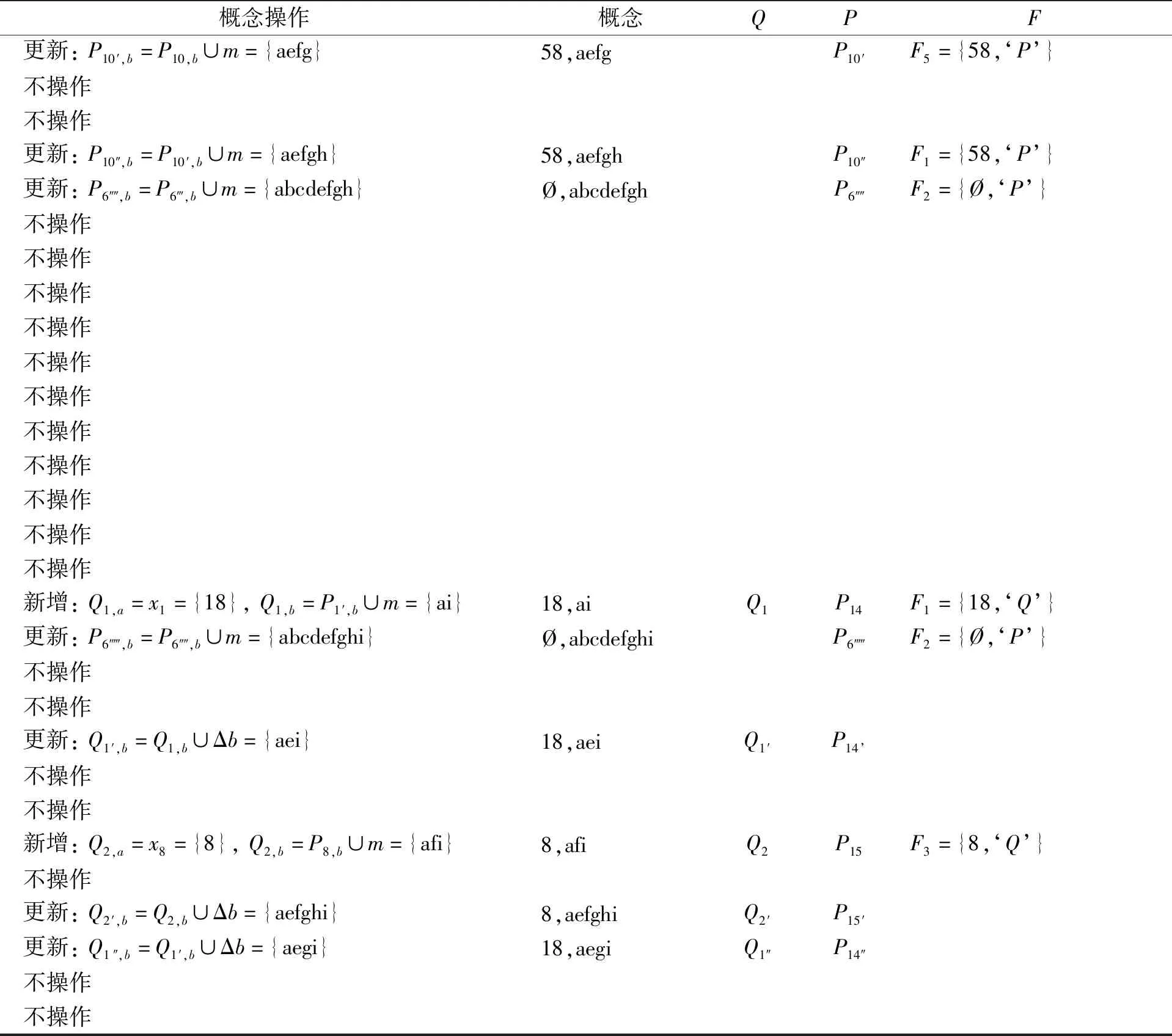
以表1中的形式背景为例。假设M中的属性处理顺序为{a,b,c,d,e,f,g,h,i}。下面3个例子演示算法的主要思路,涉及对一个任务属性进行操作的各步骤计算方法,以及相应规则的应用。完整的概念生成过程见附录A。为叙述方便,将任务属性{m}简记为m,如将g({a})表示为g(a)。
例1 对任务属性a进行操作。
初始化P1,a←U,P1,b←Ø,并初始化Q和F为空。
g(a)←{1,2,3,4,5,6,7,8},x1←g(a)∩P1,a={1,2,3,4,5,6,7,8}。x1∉Fa且x1=P1,a,根据规则3,更新P1′,b←P1,b∪m={a},同时更新F←{{{1,2,3,4,5,6,7,8},‘P’}}。因为P中只有一个概念,与任务属性a相关的概念操作结束。最后,将Q中的新增概念更新到P中,并清空Q和F。
例2 对任务属性e进行操作。对于任务属性m=e,P中已有4个概念(由e之前的任务属性a,b,c,d所生成),如表2所示。其中P1′表示概念P1已动态更新一次内涵,P2″表示概念P2已动态更新两次内涵。另外,一个任务属性开始时,Q为空,F为空。

表2 任务属性(e)的先行概念集合PTab.2 The privious concept set P of task attribute(e)
操作步骤如下。
S1求任务属性e的对象集合:g(e)←{1,4,5,8}。
S2将g(e)与表2中的外延集合Pa元素逐个求交集,并根据规则进行概念操作。
S2.1x1←g(e)∩P1′,a={1,4,5,8}∩{1,2,3,4,5,6,7,8}={1,4,5,8}。
首先,因为F为空,x1∉F。将x1与Pa中的外延逐个比较,没有与x1匹配的外延,即x1∉Pa。根据规则4,在Q中新增概念Q1,其中Q1,a←x1={1,4,5,8},Q1,b←P1′,b∪m={a,e}。同时更新F←{{{1,4,5,8},‘Q’}}。
S2.2x2←g(e)∩P2″,a={1,4,5,8}∩{2,6}=Ø,x2∉Fa且x2∉Pa。根据规则4,在Q中新增概念Q2,其中Q2,a←x2=Ø,Q2,b←P2″,b∪m={a,b,c,e}。同时更新F←{{{1,4,5,8},‘Q’},{Ø,‘Q’}}。
S2.3x3←g(e)∩P3,a={4}。x3∉Fa且x3∉Pa,根据规则4,在Q中新增概念Q3,Q3,a←x3={4},Q3,b←P3,b∪m={a,d,e}。同时更新F←{{{1,4,5,8},‘Q’},{Ø,‘Q’},{{4},‘Q’}}。
S2.4x4←g(e)∩P4,a={1,4,5,8}∩{2}=Ø。x4∈Fa且x4=Q2,a(由步骤S2.2生成),Δb←P4,b-Q2,b={a,b,c,d}-{a,b,c,e}={d},Δb≠Ø。根据规则2,更新Q2′,b←Q2,b∪Δb={a,b,c,d,e}。因x4∈Fa,所以此处无需更新F。
至此,由任务属性e生成的新增概念集合Q处理完毕。Q中的概念如表3所示。

表3 任务属性(e)的新增概念集合QTab.3 The newly-add concept set Q of task attribute (e)
S3将Q更新到P中,并清空Q和F。最后,P中的概念如表4所示。

表4 更新后的先行概念集合PTab.4 The updated privious concept set P
例2中Fa与Qa相同,未体现F作为过滤器的作用。如前所述,Qa⊆Fa,大部分情况下Fa中包含的元素多于Qa。实际上,F可以快速检测出无需更新的操作,尤其是对M中位置靠后的任务属性,F的过滤作用比较明显,如例3所示。
例3 对任务属性h进行操作。因为求解步骤与例2相似,此处进行简要说明,不再列出详细计算过程。
首先g(h)←{5,8},此时先行概念表P中由属性a~g生成的概念共有10个,具体请参考附录A。
将g(h)与P中外延集合Pa的元素逐个求交集
x1=x5=x8=x10=x11=x13={5,8}=P10′,a,
x2=x3=x4=x6=x7=x9=x12=Ø=P6‴,a
先处理x1。因为开始时F为空,x1∉Fa,且x1=P10′,a,根据规则3,更新P10″,b←P10′,b∪m={a,e,f,g,h},同时更新F←{{{5,8},‘P’}}。此后,因为x5,x8,x10,x11,x13都等于F1,a,且满足F1,c=‘P’,根据规则1,无需对概念进行操作。
同样,x2∉Fa,且x2=P6‴,a,根据规则3,更新P6″″,b←P6‴,b∪m={a,b,c,d,e,f,g,h}。同时更新F←{{{5,8},‘P’},{Ø,‘P’}}。此后,因为x3,x4,x6,x7,x9,x12都等于F2,a,且F2,c=‘P’,根据规则1,无需对概念进行操作。
从例3可见,这里F={{5,8},Ø},而Q为空,两者之间并不相等。根据xi是否属于Fa,可快速判断当前应执行哪种操作,且每次只需搜索Pa和Qa两个集合之一,节省了大量搜索与匹配的时间。
4 实验与结果分析
实验对比算法是NextClosure。实验环境:Intel Xeon E-2224G CPU,64 Gbyte RAM,Windows 10操作系统,算法采用Python3.8实现。
为提高NextClosure运行效率,设置了一个查重字典,对第1次出现的f(u)及g(f(u))写入字典,后续出现相同的f(u)时直接查表,以避免多次重复计算,其中u=A∩{1,2,…,i-1}∪{i},A是待判断的外延。另外,Python中字典类型利用Hash查找,能快速定位元素,所以NextClosure和笔者算法IUICG都采用字典存储概念,外延对应Key,内涵对应Value。背景中的每个对象对应的属性,以及每个属性对应的对象都采用预先存储的形式,以加快后续的交集运算速度。
为更好评估算法的时间性能,两个算法在不同数据集上都运行15次,并以各次的运行时间平均值作为实验结果。
4.1 实验数据集
实验数据集采用人工随机数据集。与其他文献类似,数据集主要考虑背景的对象数量|U|,属性数量|M|和属性的填充率|f| 3个参数。数据集各参数的值设置如表5所示。

表5 数据集参数Tab.5 The data set parameters
数据集包含4种类型,Net1数据集用于测试算法在不同属性数量上的时间性能。Net2数据集是Net1中对应网络的转置,|M|不变,而|U|逐渐增大,用于测试算法对|U|变化的适应性。Net3考虑了|U|和|M|不变的情况下,属性填充率变化对算法的影响。Net4用于测试笔者算法在较大规模数据集上的时间性能。各数据集对应的概念数量如表6所示。

表6 所有背景的概念数Tab.6 Number of concepts in all contexts
由表6可见,Net1和Net2数据集对应的概念数量一致,这是因为将形式背景转置,仅是将对象概念转换为属性概念,本质上对应的概念一致。
4.2 实验结果与分析
在Net1和Net2上的实验结果如图1所示。因为Net1和Net2是同一形式背景上的对象概念和属性概念的关系,将两者的实验结果对比,可以更好地了解算法的时间性能和适应场景。其中,图例后缀为|U|的表示该折线是关于背景中对象数量|U|变化的实验结果,即在Net2上的实验结果。相应的,图例后缀为|M|的是在Net1上的实验结果。因NextClosure-|U|在|U|变大时运行时间快速增长,此处只列出其在Net2前3个网络上的实验结果。

图1 在Net1和Net2上的运行时间性能比较Fig.1 Runtime performance comparison on Net1 and Net2
图1结果表明,在Net1和Net2上,IUICG算法的时间性能都优于NextClosure算法,且在Net2上两者的运行时间有很大差异。这是因为NextClosure每生成一个外延都要进行以下运算:首先计算u=A⊕i,再进行f(u)和g(f(u))运算,最后再对A NextClosure算法在Net1上的时间耗费远小于在Net2上的。与NextClosure相反的是,IUICG在Net2上具有更好的时间性能,其在Net2上的时间复杂度接近线性,其中,在Net26(|U|=3 000)上的运行时间约为4.5 s。 通过分析两种算法的实现过程,可以看出,NextClosure中,生成大于上一个外延的最小外延,可能需要遍历全部对象,且存在大量的交集操作,随着对象数量增加,其所需的时间也快速增加。IUICG在每个属性上进行概念操作,每增加一个属性,就需要与已有的概念进行一轮交集运算,所以随着属性数量增加,IUICG的运行时间也随之增加。 两种算法具有不同的适应性,NextClosure对|U|的变化更为敏感,而IUICG对|M|的变化更为敏感。但总体上,IUICG比NextClosure具有更优的时间性能。 基于上述实验结果,笔者提出以下操作方案。对对象数量和属性数量有较大差异的数据集,若属性数量大于对象数量,将形式背景进行转置,用IUICG算法先得到背景的属性概念,再将其转换为对象概念,这将有效提高概念生成速度。 Net3中,在|U|和|M|不变的情况下,逐渐增加属性的填充率,其对应的概念数量快速增长。如表6所示,Net35的概念数量还不到100万,而Net36的概念数接近400万。两个算法在Net3上的的运行时间对比结果如图2所示。图3给出了IUICG算法在较大规模|U|的数据集上的运行效率。 图2 在Net3上的运行时间性能比较 图3 在Net4上的实验结果Fig.2 Runtime performance comparison on Net3 Fig.3 Experimental results on Net4 其中NextClosure只列出前4个网络的实验结果,其在Net35(|f|=0.25)和Net36(|f|=0.3)上的运行时间分别约为8 000 s和30 000 s。而IUICG算法在Net36上的运行时间约为110 s。两者之间的差异较大,原因与前面的分析相同。可见,IUICG对属性高填充率的网络仍有较好的适应性。 因为NextClosure在此类数据集上的性能较差,此处不予比较。IUICG的运行时间会随着|U|增大,但仍呈现接近线性的时间复杂度。 笔者提出一种增量更新内涵的概念生成算法IUICG。算法根据任务属性对概念搜索空间进行划分,并引入外延过滤集合,加快了候选外延的判断速度。提出概念操作规则,证明了规则的正确性,为快速更新内涵和新增概念提供了理论依据。在各种人工随机数据集上的实验结果表明,IUICG具有较好的时间性能。 IUICG中,生成候选外延仍然需要遍历已有概念,如何有效缩减候选外延是下一步的研究重点。另外,分析概念间的生成与包含关系,在高效生成概念的过程同时构建概念间的层次结构也有待于研究。 附录A IUICG算法在表1背景上的运行步骤。 mg(m)xi满足条件适用规则{12345678}a{12345678}x1={12345678}x1notinFaandx1=P1,a规则3b{26}x1={26}x1notinFaandx1notinPa规则4c{26}x1={26}x1notinFaandx1=P2,a规则3x2={26}x2=F1,aandF1,c=‘P’规则1d{2347}x1={2347}x1notinFaandx1notinPa规则4x2={2}x2notinFaandx2notinPa规则4e{1458}x1={1458}x1notinFaandx1notinPa规则4x2=Øx2notinFaandx2notinPa规则4x3={4}x3notinPaandx3notinQa规则4x4=Øx4inFaandx4=Q2,aandΔb=P4,b-Q2,b={d}规则2f{3578}x1={3578}x1notinFaandx1notinPa规则4x2=Øx2notinFaandx2=P6′,a规则3x3={37}x3notinFaandx3notinPa规则4x4=Øx4=F2,aandF2,c=‘P’规则1x5={58}x5notinFaandx5notinPa规则4x6=Øx6=F2,aandF2,c=‘P’规则1x7=Øx7=F2,aandF2,c=‘P’规则1g{1568}x1={1568}x1notinFaandx1notinPa规则4x2={6}x2notinFaandx2notinPa规则4x3=Øx3notinFaandx3=P6″,a规则3x4=Øx4=F3,aandF3,c=‘P’规则1x5={158}x5notinFaandx5notinPa规则4x6=Øx6=F3,aandF3,c=‘P’规则1x7=Øx7=F3,aandF3,c=‘P’规则1x8={58}x8notinFaandx8=P10,a规则3x9=Øx9=F3,aandF3,c=‘P’规则1x10={58}x10=F5,aandF5,c=‘P’规则1h58x1={58}x1notinFaandx1=P10′,a规则3x2=Øx2notinFaandx2=P6‴,a规则3x3=Øx3=F2,aandF2,c=‘P’规则1x4=Øx4=F2,aandF2,c=‘P’规则1 (续表) (续表)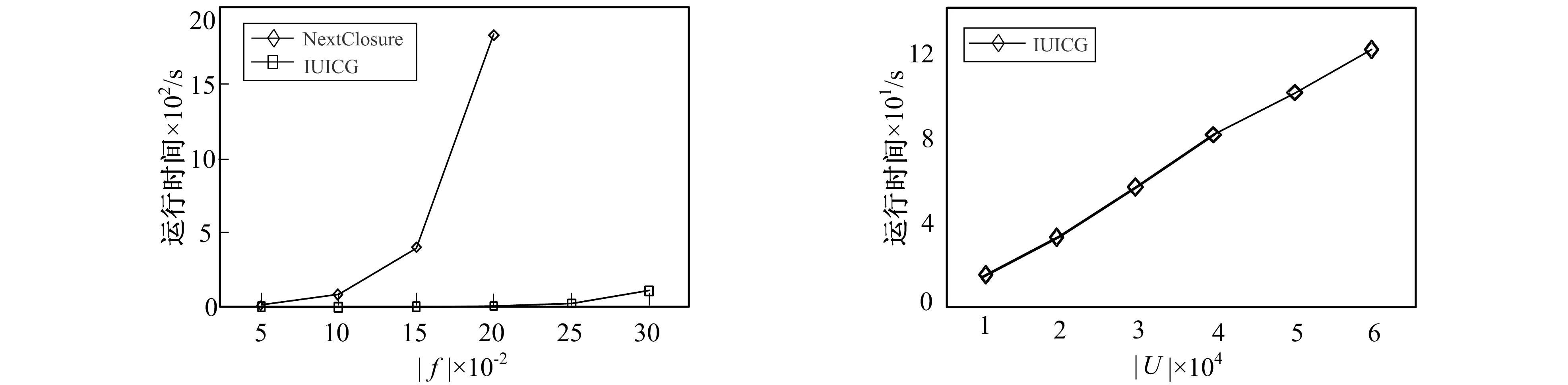
5 结 语