非参数估计下的金融风险审慎评估方法

毛明扬

(广州华商学院 数据科学学院,广州 511300)

0 引 言

全球各类经济体系内部相互之间的金融关系日渐增多,金融风险和危机也表现出系统性关联。金融市场的开放性与融合性,在增加资本运转、加强资源配合效率的同时,也给金融市场带来了机遇和挑战[1]。在金融一体化阶段,若市场经济发生金融危机时,其风险蔓延速度极快,系统性的金融风险很有可能导致市场实体经济价值损失巨大,且使人们对金融系统失去信心,产生支付危机、货币贬值危机,继而致使全球性经济下滑,所呈现的严重后果不堪设想[2]。现阶段,我国潜在的金融风险实质上是体制风险,涉及跨经济领域、跨市场的金融活动。简单的依靠机构监管已经很难使金融风险得到妥善解决,如若不做出根本性改变,建立一个稳定长效的监管机制,一定会增加面对突发性金融风险的价值成本和社会负面效应[3]。

审慎评估的出发点是要改善传统货币举措和微观监管在抵抗风险方面的不足,把金融业作为一个有机整体,管理的目标要注重金融体系在目前及未来时段经济运转的深层面问题。在实行经济可持续发展的同时,预防和监管跨行业、跨期限的整体金融风险,维系金融平稳发展是审慎评估的最终目标。

可预测的风险亟须密切监视,而不可预测的风险同样不能疏忽遗漏[4]。由于金融市场对国民经济占据举足轻重的地位,因此如何有效地权衡、控制风险已成为学术界研讨的核心内容。

综合上述观点,笔者提出一种基于小波分析与非参数估计的金融风险审慎评估方法,通过建立纳入概率分布的风险评估模型,联合小波分析与非参数估计的参变量厘定方法,进一步确定金融风险的损失数目,使用贝叶斯后验概率分布得到马尔科夫链,对未知变量模拟,应用稳定分布抽样点推算蒙特卡洛积分,增强金融风险审慎评估的有效性。

1 基于纳入概率分布的风险评估模型

笔者提出两种纳入概率分布族。使用QI(α,β,δ,μ)表示第1类纳入分布概率族[5],其表达式为

(1)

其中α,β,δ,μ表示参变量,且满足α,β,δ∈R+,μ∈R,上标识(α)在α>0的情况下可用下列算子表达

(2)

其中μ表示位置参变量,δ表示尺度参变量,β参变量大小可衡量尾部对称性。在β=1的情况下,该纳入分布为均衡状态;在β≠1的状态下,即表明纳入分布的右尾比左尾厚。参变量α能立体地展现出纳入分布的尾部厚度,若α值较小,则表示纳入分布的尾部更厚[6]。

第1类纳入概率分布族QⅠ(α,β,δ,μ)具有明显的分布密度,可将其表示为

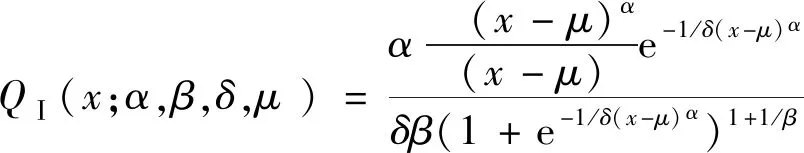
(3)

其中x∈(-∞,μ)∪(μ，+∞),由于第1类纳入概率分布族拥有明显的分布密度方程式,因此能直接使用极大似然估算方法推导出参变量α、β、δ、μ。

第2类纳入概率分布族使用QⅡ(y;α-,α+,β-,β+,μ)进行表达,其核心作用是拟合具有特殊不平稳尾部特征的数据分布状态,其函数表达式为

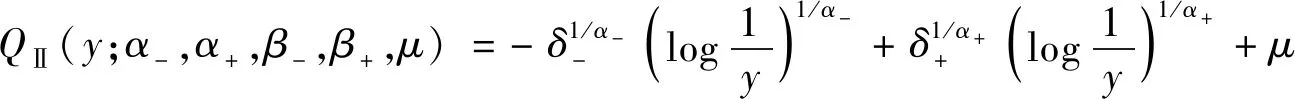
(4)

其中模型参变量α-,α+,β-,β+∈R+,且μ∈R,同时最为关键的是参变量α-≤1、α+≤1的概率分布状态。和第1类分布相同,参变量α-、α+也是用于权衡左右尾部的厚度情况。

使用式(3)，式(4)模型,可简单地估算出金融资产获益与相应的风险系数[7]。假设用R(t)表示某项资产组合在持有期T中的收益率,VαRθ表示其资产组合在置信水准1-θ(0<θ<1)下的风险系数,则可得

VαRθ=-q(θ)

(5)

其中q(θ)表示R(t)的样本纳入概率函数。

2 基于小波分析与非参数估计的参变量厘定

在构建纳入概率分布风险评估模型后,为明确金融风险造成的价值损失,保证金融产业的平稳运行,为此笔者提出了基于小波分析与非参数估计的参变量厘定方法。

小波分析是时域分析的一种,其在时域与频域方面均具有优秀的局部化特征,拥有多分辨率解析优势。小波转换在低频区域拥有较高的频度分辨率及较低的时段分辨率,在高频区域拥有较高的时段分辨率及较低的频度分辨率,可称得上是信号分析显微镜[8]。使用小波分析原则,可以将信号分解,将其划分为多层传输至频度信道内。因为分解后的信号频度因子比初始信号更加单一,需要对信号进行平滑处理,使分解后信号的稳定性高于初始信号,证明小波分析的优越性。

多分辨分析是一种将信号空间分解的方法,在此前提下,获得Mallat算法。利用该算法能把信号实行层级分解,令每个层分解的结果为上一次分解获得的低频信号,然后再将其分解成低频与高频,具体方法为

(6)

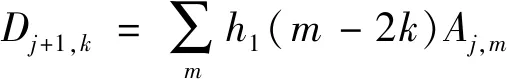
(7)

其中j表示分解尺度,k、m表示位移系数,Aj,m表示低频区域尺度系数,Dj+1,k表示高频区域小波系数,h0、h1依次表示低通与高通滤波器。

使用分解后的小波系数能重建初始序列,希波系数的重建表达式为

(8)

从第1层进行分解,其结果包括高频区域D1与低频区域A1,其次针对低频区域进行更深入分解,其结果拥有高频区域D2与低频区域A2。以此类推,持续信号分解,通过4次分解后,初始信号A被分解成

A=A4+D4+D3+D2+D1

(9)

其中D1、D2、D3、D4依次表示第1层～第4层通过分解所获得的高频信号,A4表示第4层分解获得的低频信号,分解层数的个数可按实际情况决定。

若X1,X2,…,Xn为一元持续全局样本,在随机点x位置的核密度函数为

(10)

(11)

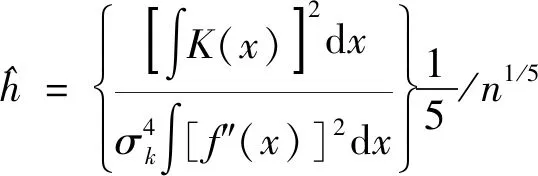
(12)

若式(12)符合N(0,σ2)正态分布,则核函数K(x)即为高斯核函数,所以有

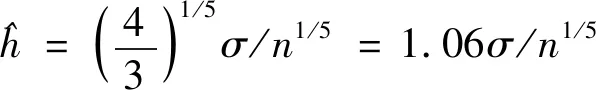
(13)

多数情况下,σ使用样本标准差S替换,同时,因为真实数据通常与正态分布呈偏离状态,因此系数1.06降为0.8会更加合理。

3 基于蒙特卡洛算法的模型求解

计算金融风险价值损失,可直接观测金融风险程度。将风险模型进行求解可进一步提升金融风险审慎评估,将资金利用率发挥到最优。

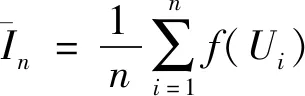
(14)

(15)

其中St表示t时段的资产数目,μ表示平均值,σ表示资产浮动率,ε表示随机变化参数。设想处于正态分布的前提下,σ表示标准差,ε表示随机变化参数。在蒙特卡洛模拟算法内,用σ表示收益率的浮动性。

使用极大似然估计,经过迭代得到的估算值要符合渐进性与相同性,这只有在大样本情况才能成立。

蒙特卡洛算法的出现为处理贝叶斯后验积分难以计算的问题,提供了新的运算思路。马尔科夫链蒙特卡洛方法(MCMC：Markov Chain Monte Carlo)将随机过程内的马尔科夫链加入蒙特卡洛算法内,将抽样概率分布随蒙特卡洛算法的计算过程而不断发生变化,把动态模拟转化为真实运算[12]。MCMC方法能利用下面推导步骤进行演算。

将处于t时段的随机变化参数θ表示为θt,θt也是状态空间Θ内的一个值,若θ在Θ中不同数值之间的移动概率只依靠于θ的目前状态,与之前时段的空间状态无关,若处于

Pr(θt+1|θ1…θt)=Pr(θt+1|θt)

(16)

状态下,则将随机序列{θt,t≥0}作为马尔科夫链。假设{θ(t)}t≥0是状态空间Θ内的齐次马尔科夫链,则能得到移动纳入概率函数

(17)

其中p(θ,θ*)表示移动核。

针对某个分布π(θ),通常状态下,不管原始状态θ0是什么类型分布,经过较长时间后,马尔科夫链会渐渐忽视其原始状态,表明π(θ)既不依靠原始状态,也不依靠时段t,则θt的边际分布为π(θ)。

因此,不管原始数值如何,θt会慢慢约束至同一个分布内,也就是稳定分布。而在约束没有出现的前m次迭代中,π(θ)还不是任意状态的边际分布,应将前面m次迭代数值进行剔除,仅使用后面n-m个迭代值采取估算,因此有

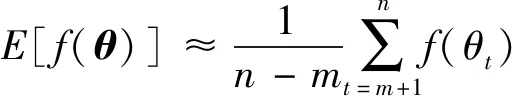
(18)

从模拟推导角度出发,建立的移动核将已知的纳入概率分布π(θ)变为稳定分布。若t维随机矢量ζ=(ζ1,…,ζt)拥有联合分布π(ζ1,…,ζt),则函数[f(ζ)]的后验数学期望为

(19)

式(19)内的积分运算过程较为繁杂,因此可利用MCMC方法进行简化计算,具体步骤如下。

1) 在ζ内设计出恰当的马尔科夫链,移动核是P(),让其对照稳定分布π(ζ)；

2) 通过ζ内某一点ζ0,使用步骤1)内的马尔科夫链生成点序列ζ1,…,ζn；

3) 剔除估算E[f(ζ)]之前的m个预判迭代数值,则随机函数f(ζ)的期望估计为

(20)

使用MCMC方法对未知变化参数采取抽样模拟,通过一定的抽样次数后,马尔科夫链逐渐趋向于平稳状态,此时的稳定状态分布就是求解出的后验分布,其次使用稳定状态分布内的抽样点推算蒙特卡洛积分,完成精确的金融风险审慎评估,对风险拥有正确估判。

4 仿真实验

使用基于Matlab平台,对笔者方法、EVT-POT(Extreme Value Theory-Peaks Over Threshold)方法和SKST方法进行仿真实验,验证笔者方法的优越性。

图1给出了近十几年的深成指数收益率浮动情况,在3 562个测量指数比较中,EVT-POT、SKST方法的突破次数依次是58次和62次,突破率是1.368 5%和1.489 6%。而使用笔者方法的突破数量为29次,其突破率为0.526 7%,明显优于其他两种方法,可有效对金融风险采取精准控制,将风险系数降到最低。

图1 风险控制对比Fig.1 Comparison of risk control

除了突破率外,还对3种方法进行损失函数对比,验证其金融风险概率,具体如表1所示。

表1 损失函数分析Tab.1 Loss function analysis

从表1可以看出,由于EVT-POT、SKST方法均为现阶段较好的参数方法,所以都能通过无条件覆盖测试、独立性测试和条件覆盖测试,但笔者方法的损失函数值最低,证明笔者方法为最优损失函数,而其他两种方法具备一定的局限性,不能兼顾突破次数和突破过程中的损失规模,由此证明了笔者方法的实用性。

5 结 语

为提升金融风险预判精度,笔者提出一种基于小波分析与非参数估计的金融风险审慎评估方法。通过建立纳入概率分布风险评估模型,确定风险相关系数；利用小波分析与非参数估计相结合的参变量厘定方法,保证金融产业稳步运转；采取蒙特卡洛算法对模型进行求解,实现金融风险的有效监管,在金融风险机制中发挥了重要作用,可极大改善经济风险带来的损失,拥有较强的实用性,鲁棒性较高。