变负荷模式下电力多级冗余数据精细化校验算法

余旭阳,严慧峰,向 颖,徐秀敏

(1.国网湖南省电力有限公司 发展策划部,长沙 410007;2.北京国电通网络技术有限公司 规划与计划管理业务事业部,北京 100085)

0 引 言

随着物联网技术的飞速发展,电网规模持续增加,电网数据呈爆炸式增长[1-2]。因此,如何在大规模的电网数据中获取有效且准确的电网数据成为当前研究的热点,国内有相关专家针对该方面的内容进行了大量研究。陈容等[3]在已有固定位宽并行算法基础上,通过公式递归法进行并行计算,完成循环冗余校验。朱智燊等[4]主要采用信道对Modbus数据进行哈希检验。由于以上两种算法未能对采集到的电力数据进行聚类处理,导致校验结果不理想、用时增加等问题。为此,笔者提出一种变负荷模式下电力多级冗余数据精细化校验算法,经实验测试证明,所提算法不仅能有效降低校验用时、误差以及额外存储开销,同时还能有效提升查全率,得到了满意的校验结果。

1 算 法

1.1 电力数据采集

电力系统可划分为数据中心，中间站，用户端3部分。

一个数据中心站同时对应多个中间站,每个中间站又对应多个用户。电力数据将不间断地在用户处形成,用户i对应的中间站每间隔一个时间段t将采集一次用户的电力数据ui,同时将全部的电力数据在本地进行缓存。一个中间站对应N个用户,则中间站在t时刻采集的电力数据为f=[u1,u2,…,uNt]T,因此经过M个t时间间隔,中间站将当前缓存的电力数据发送至数据中心,对应的计算式为

(1)

其中F表示在第i采样时刻的电力数据；N表示用户总数；M表示采样总间隔。

在对电力数据监测过程中,邻近时刻的监测数据具有较强的关联性。以下主要通过数据的相关性完成数据采集[5-6]。

稀疏性是压缩感知理论的基础,通过信号的可稀疏性判定能否恢复原始数据。其中,电力数据主要包含以下几个步骤。

1) 电力数据压缩。当接收到原始电力数据对应的状态信号f,进而借助测量矩阵Φ得到对应的观测信号y=Φf。

2) 电力数据存储或传输。将经过压缩处理的观测信号y进行存储或传输。

3) 数据恢复阶段。接收端接收到的观测信号为y=Φf,通过测量矩阵和稀疏字典将其转换为稀疏信号,进而达到恢复数据的目的。

稀疏矩阵是电力状态信息进行稀疏化的转换矩阵,获取对应的电力状态数据f=[u1,u2,…,uN],经过稀疏化处理获取稀疏向量,最终得到稀疏矩阵。

设电力数据为F,通过

(2)

(3)

测量矩阵在进行数据压缩以及重构过程中都需要使用,设Φ表示测量矩阵。优先通过Φ对电力信号f进行压缩处理,获取对应的观测信号y。结合压缩感知理论可以有效恢复原始电力数据。其中Φ和ψ两者之间的相关系数为

(4)

(5)

1.2 电力数据聚类处理

谱聚类是一种全新的聚类算法,主要用于数据聚类优化[9-10]。其中谱聚类能准确识别不同形状的簇,同时还能获取比较满意的聚类结果。其中谱聚类主要包含以下几个步骤。

1) 构建数据样本集关系属性对应的矩阵R。

2) 计算R的前k个特征值,组成特征向量集,进而构建对应的向量空间S。

3) 通过聚类方法对S中的电力数据进行聚类处理,同时将得到的聚类结果映射到对应的空间中。

由于不同类型的电力数据结构是完全不同的,需要优先通过NJW(Ng-Jordan-Weiss)算法对前k个特征向量组成的子空间进行聚类处理。同时,给出特征向量空间S形成的详细操作步骤。

1) 建立原始电力数据的相似度矩阵W,矩阵内的元素Wij为

(6)

其中d2(xi,xj)表示两个样本之间的欧氏距离；σ表示样本的尺度参数。

2) 构建标准的Laplacian矩阵Lsym。

3) 设定参数M的具体取值范围。

4) 在上述操作基础上,对M个特征值对应的特征向量矩阵进行求解,进而形成矩阵Y,将其应用于S中。

由于已有的K-means算法对初始中心的选取十分敏感,不能得到全局最优,导致NJW算法的稳定性下降。为此,引入遗传算法[11-12],最终完成电力数据聚类,详细操作步骤如下。

对簇心序列进行实数编码,通过随机分配方式形成初始种群,对每个样本进行编号,根据编号将其划分到对应的簇中。重复以上操作步骤,直至完成种群的初始化处理。

遗传聚类算法的目标函数T和K-means算法需要保持一致,即两者的总类内方差相同。利用

(7)

给出具体的适应度函数计算过程。其中Ti表示种群中第i个个体对应的目标函数取值；Tmin和Tmax分别表示最小和最大的目标函数值；α表示个体的淘汰加速度指数。

考虑到基因个体的无序性,为有效防止个体之间出现错误匹配,需要对全部个体进行排序,选取距离最近的基因进行一一匹配。以下给出详细步骤。

形成两个个体之间对应基因位的距离矩阵D如下

(8)

其中Dij表示两个不同个体之间的欧氏距离。

获取矩阵D中最小元素,同时对其进行基因配对,将矩阵的第i列和第j列元素的取值全部设为0。获取矩阵中的最小非零元素,将对应的基因进行匹配,该行对应的元素取值设为0。重复以上操作步骤,直至全部个体完成基因配对为止。

当种群中的全部个体经过交叉和变异等相关操作后,需要计算初始样本集V和各类序列之间的距离,通过最近距离原则确定类心,将新的个体设定为此次迭代的最终结果,同时将其代入到下一次的迭代中。

在上述分析基础上,得到以下遗传聚类优化算法操作步骤[13-14]。

1) 将特征向量矩阵按照行进行划分,形成聚类空间特征样本集,同时对不同的个体进行编码,形成初始种群。

2) 计算初始种群的适应度函数,设定迭代次数。

3) 结合遗传算法对第i代种群进行选择以及交叉等相关操作,进而获取全新的种群。

4) 判断迭代次数是否达到设定的标准,假设达到,则返回至步骤3)；反之,则停止迭代,同时选择种群中适应度取值最大的个体设定为最终的聚类结果。

5) 将初始特征样本集按照离最终结果距离的远近[15]进行编号,获取特征向量空间对应的聚类划分结果。

1.3 变负荷模式下电力多级冗余数据精细化校验

综合评价是客观地对评价对象进行合理全面的评价。其中,可通过数学模型将多个评价指标经过一系列操作整合成一个综合评价值,对应的函数如下

yxy=f(ω,x)

(9)

其中yxy表示综合评价值；ω表示评价指标的权重向量。

针对实际问题,需要对各个评价对象的相关因素进行分解,进而构建判断矩阵。逐一对矩阵中的各项评价指标进行测试,得到判断矩阵如下

(10)

通过层次分析法的相关原理,能准确推导出判断矩阵各列的和,同时借助计算得到判断矩阵的系数矩阵

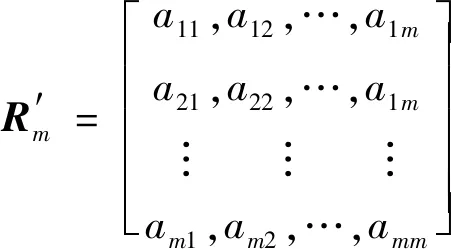
(11)

求解矩阵中的特征根和特征向量,同时对其一一进行检验,判断矩阵是否需要修改或重建。其中,一致性检验指标为

(12)

其中λmax表示矩阵中最大的特征根。

根据电网数据的类别划分,可构建对应的指标模型。在变负荷模式下,对全部电力多级冗余数据进行合理性检验,判断数值是否在合理的范围内,是否出现较大的偏差。分析不同类型电力数据的相关性,制定对应的相关性标准,得到对应的评价指标。通过评价指标对不同的电力数据进行打分,同时制定对应的电力多级冗余数据精细化校验准则。通过制定的精细化校验准则一一对电力多级冗余数据进行校验,将冗余数据剔除。

2 仿真实验

为验证所提变负荷模式下电力多级冗余数据精细化校验算法的综合有效性,实验选取2019年H城市的电网数据作为测试数据。

1) 查全率。分析每个算法在不同时段的查全率变化情况,对应的公式如下

(13)

图1给出了3种算法的查全率对比结果。

从图1可以看出,所提算法的查全率处于比较稳定的状态,而另外两种算法的查全率则呈直线下降趋势,充分说明所提算法能准确检测出多级电力数据中的冗余数据。

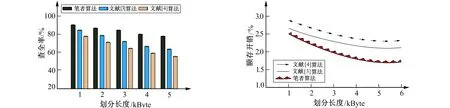
图1 不同算法的查全率对比结果 图2 不同算法的额外存储开销对比结果Fig.1 Comparison results of recall of different algorithms Fig.2 Comparison results of extra storage overhead of different algorithms

2) 额外存储开销。实验对比了3种不同算法的额外存储开销,结果如图2所示。

从图2可知,随着划分长度的持续增加,每个算法的额外存储开销开始呈直线下降趋势。但相比另外两种算法,所提算法的额外存储开销明显更低,充分验证了所提算法的优越性。

3) 精细化校验性能测试。为进一步验证所提算法的优越性,测试对比3种不同算法的校验结果如表1所示。

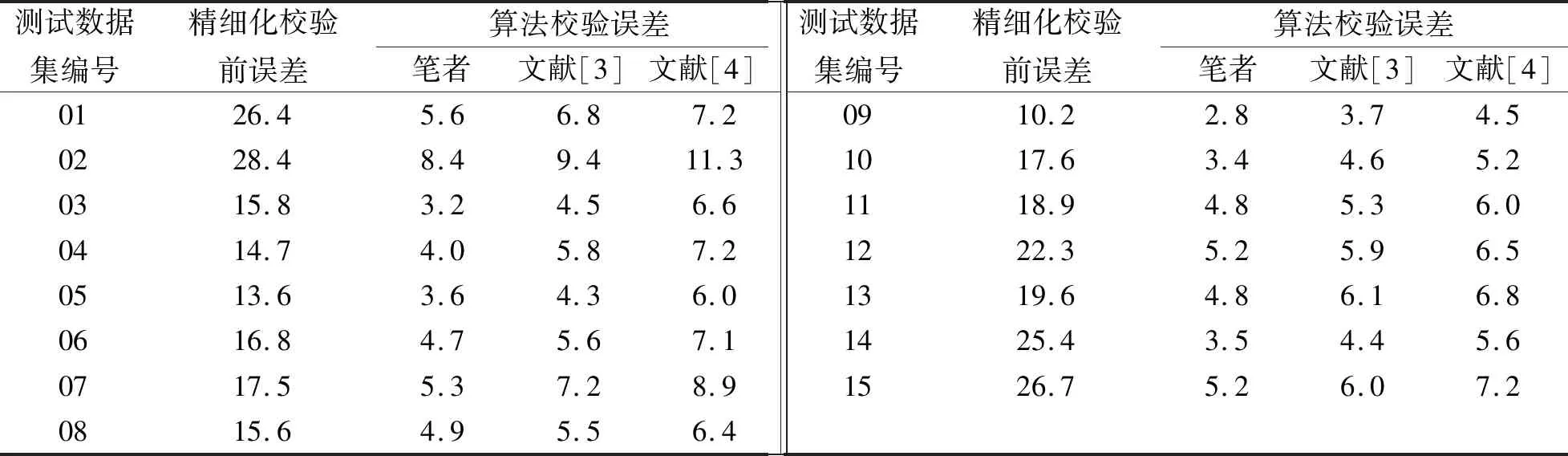
表1 不同算法的精细化校验结果对比Tab.1 Comparison of refined verification results of different algorithms (%)

从表1可知,所提算法的精细化校验误差明显低于另外两种算法,主要是因为所提算法在进行校验前期,对采集到的全部电力数据进行了聚类处理,根据聚类结果可以更好地完成精细化校验,全面提升电力多级冗余数据精细化校验结果的准确性。

4) 精细化校验用时。实验对比了3种不同算法的精细化校验用时,结果如图3所示。

图3 不同算法的精细化校验用时对比结果Fig.3 Comparison results of fine check time of different algorithms

从图3可知,所提算法的用时明显低于另外两种算法,说明所提算法能以较快的速度完成校验,充分验证了所提算法的优越性。

3 结 语

笔者针对传统算法存在的不足,设计并提出一种变负荷模式下电力多级冗余数据精细化校验算法。经实验测试证明,所提算法能有效提升查全率,降低额外存储开销和精细化校验用时,得到了更加准确的校验结果。